Нефтегазодобыча всегда являлась сложным технологическим процессом, поэтому в ней в полной мере востребованы информационные технологии, применяемые и для создания цифровых трехмерных моделей месторождений нефти и газа. Информационные модели используются для оценки запасов и состояния разработки, прогнозирования технологических показателей для выбора оптимальной стратегии выработки залежей углеводородного сырья, математических расчетов, автоматизации систем обработки.
Основными задачами при визуализации трехмерной геолого-технологической модели являются правильная обработка исходных геологических данных и поиск оптимальных алгоритмов представления информации с учетом возможностей современных вычислительных ресурсов. Каждое месторождение уникально, следовательно, некорректное использование исходных данных и методов воздействия на пласт могут привести к непоправимым последствиям, что затруднит дальнейшую разработку [1]. Для избежания этого каждая технология воздействия на продуктивный пласт до практической реализации должна быть обоснована с помощью математических расчетов и состоять из качественных исходных данных, полученных в ходе исследований. На основе полученной модели с множеством выходных данных специалисту требуется оценить степень риска повреждения пласта, а также грамотно воспользоваться полученными данными при решении поставленных задач. Разрабатываемый программный комплекс применим для изучения различных характеристик пластов, содержащих одиночные скважины, группы скважин или несколько скважин, связанных как единый комплекс [2]. Преимущество моделирования заключается в том, что оно дает возможность в единой системе комплексно проанализировать все тесно взаимосвязанные характеристики пластов и флюидов.
Формирование геометрии ячейки пласта
Разработка виртуальной трехмерной модели по исходным геологическим данным – сложная вычислительная задача, для решения которой оптимальна аппроксимация данной модели сеткой треугольников. Процесс разбиения поверхности на треугольники называется триангуляцией [3].
При моделировании объекта возникает задача определения необходимого числа полигонов. Исходные геологические данные представлены в виде множества выпуклых многоугольников с 8 вершинами. Рассматриваемый многоугольник состоит из 6 сторон, каждую из которых можно представить 2 треугольниками, то есть для построения одной ячейки модели необходимо использовать 12 полигонов. Каждой вершине треугольника присваивается свой индекс, тогда вся фигура будет состоять из 36 индексов.
Существует несколько подходов к построению многоугольника для отображения в трехмерной сцене. Один из них – построение полигональной сетки без индексов, состоящей из 36 вершин. Такой подход является ресурсоемким, так как происходит прорисовка большого количества вершин, следовательно, увеличивается нагрузка на видеокарту, особенно при визуализации трехмерной модели со значительным числом многоугольников.
Другой подход подразумевает использование 8 вершин и 36 индексов, позволяя снизить количество отображаемых вершин и повысить общую производительность визуализации. Однако при этом модель освещается некорректно – происходит неправильное отражение света от сторон многоугольника, так как нормали вершин являются результирующими.
Нормаль – это вектор к поверхности в некоторой точке, перпендикулярный поверхности (то есть касательной к ней плоскости) в этой точке. Существуют два основных способа задания нормали:
– нормаль в вершине определяется нормалью к одной примыкающей грани (в каждой точке своя нормаль);
– нормаль в вершине определяется нормалями ко всем примыкающим граням (результирующая нормаль).
Одним из решений проблемы является присвоение нескольких нормалей одной вершине, однако графические интерфейсы OpenGL и DirectX не позволяют осуществлять привязку нескольких значений одного свойства к конкретной вершине, поэтому добавление отдельных вершин для каждой стороны многоугольника позволит задать свое значение нормали для соответствующей вершины. Так как данные о позиции вершин многоугольника есть только для 8 точек, выполняется их копирование в заданном порядке для создания 24 вершин. Следовательно, сторона многоугольника будет иметь 4 вершины, общее количество сторон равно 6. Таким образом, на каждую точку будет приходиться одна нормаль, что позволит корректно отобразить виртуальную трехмерную модель многоугольника.
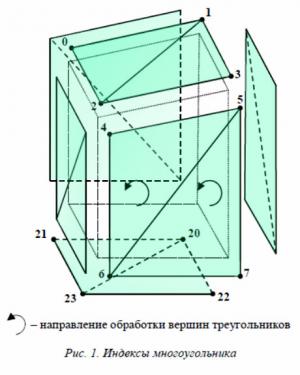 Для прорисовки применяются 36 индексов, лежащих в отрезке от 0 до 23, в соответствии с количеством точек (рис. 1). Делается это для того, чтобы каждая вершина треугольника имела свой индекс, отличный от соседних вершин.
Для прорисовки применяются 36 индексов, лежащих в отрезке от 0 до 23, в соответствии с количеством точек (рис. 1). Делается это для того, чтобы каждая вершина треугольника имела свой индекс, отличный от соседних вершин.
При построении данной модели нужно также определиться с выбором направления обхода вершин треугольников. В рассматриваемом примере был выбран обход против часовой стрелки, применяемый по умолчанию в OpenGL, начиная с нулевой и заканчивая 23-й точкой: 0, 2, 1; 1, 2, 3; 4, 6, 5; 5, 6, 7 и т.д. (рис. 1).
Вычисление нормалей для каждой вершины
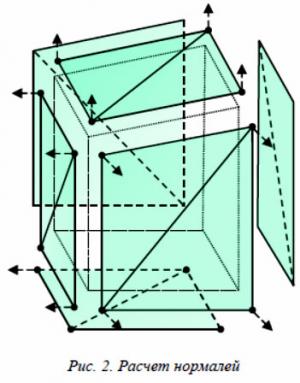 Основываясь на том, что на каждую точку приходится одна нормаль (рис. 2), осуществляется построение нормали к поверхности. Для этого нужно взять одну из сторон многоугольника, выбрать три точки (например, 0, 1 и 2) и определить, принадлежат ли они одному треугольнику. Если условие выполняется, то для данных точек вычисляются координаты векторов и
Основываясь на том, что на каждую точку приходится одна нормаль (рис. 2), осуществляется построение нормали к поверхности. Для этого нужно взять одну из сторон многоугольника, выбрать три точки (например, 0, 1 и 2) и определить, принадлежат ли они одному треугольнику. Если условие выполняется, то для данных точек вычисляются координаты векторов и 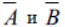 :
:
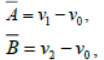 (1)
(1)
где v0, v1, v 2 – координаты точек 0, 1, 2.
Получив два вектора, вычисляем координаты вектора нормали как произведение векторов 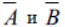 с нормированием итогового вектора:
с нормированием итогового вектора:
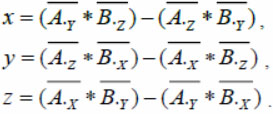 (2)
(2)
Вектор называется нормированным, если сумма квадратов его элементов (компонент, координат) равна 1 [4]. Чтобы нормировать вектор, надо все его элементы умножить на число
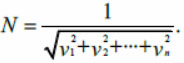 (3)
(3)
Знаменателем в формуле (3) является длина вектора (L):
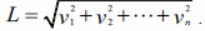 . (4)
. (4)
Тогда нормированный вектор нормали
Normal = (x * N, y * N, z * N), (5)
где x, y, z – координаты по соответствующим осям.
Данный алгоритм выполняется для всех точек многоугольника. Так как каждая сторона многоугольника состоит из двух треугольников, у которых есть две общие точки, при выполнении алгоритма на каждую общую точку придется по две нормали, что приведет к некорректному освещению данной модели. Чтобы избежать подобной ситуации, нужно произвести суммирование двух нормалей смежных точек треугольников для вычисления результирующей нормали. После этого выполняются конечное приведение вектора к единичной длине и занесение в итоговый массив нормалей многоугольника для передачи его в OpenGL [5].
Алгоритм определения текстурных координат
Для сопоставления вершин полигональной сетки с определенными пикселями в текстуре (текселями) применяются текстурные координаты. Текстурные координаты представляют собой два числа U и V с плавающей точкой для осей X и Y текстуры, значения которых лежат в отрезке [0;1]. В рассматриваемом случае для вычисления текстурных координат требуется учитывать размер текстуры – двухмерного растрового изображения, которое накладывается на поверхность объекта и позволяет придать поверхности характерные черты и детали. В первую очередь необходимо выбрать размер текстуры, которая вместила бы цветовую информацию обо всех ячейках геометрической модели нефтяного пласта. Размер текстуры выбирается в зависимости от количества ячеек, например, для модели из 50 тысяч ячеек потребуется текстура не менее чем 256х256 (так как видеокарты оптимизированы под размер текстур, кратных степени числа 2), что позволит вместить в себя 65 536 цветовых значений ячеек. Остальная часть текстуры будет заполнена однородным цветом, например, черным. Следует учесть, что применение текстуры позволяет экономить память в отличие от передачи значений цветовых компонент для каждой вершины каждой ячейки [6].
Максимальное значение координат U и V соответствует выбранному размеру текстуры (в данном случае (256;256)). Для получения значения по оси U сначала необходимо определить координату пикселя по оси X, поделив номер обрабатываемой ячейки геометрии нефтяного пласта на размер текстуры по соответствующей оси с использованием целочисленного деления с остатком. Например, 278 mod 256 = 22. Затем полученное значение делится на размер текстуры по соответствующей оси: U = 22:256 = 0,0859.
Для первого ряда текстуры значение координат TC по оси V неизменно и равно 1. При достижении максимального значения по оси U и переходе на следующий ряд значение TC по оси V будет рассчитано по формуле
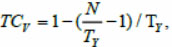 (6)
(6)
где TCv – текстурная координата по оси V; N – индекс обрабатываемой ячейки геометрии; TY – размер текстуры по данной оси.
Для оси V движение происходит от максимального значения к минимальному (от 1 до 0). Это связано с тем, что в OpenGL начало координат находится в левом нижнем углу, другими словами, построение текстурных координат будет происходить сверху вниз, что позволит упростить создание текстуры. Результатом выполнения алгоритма станет массив со значениями (U; V), который будет загружен в OpenGL.
Однако у данного алгоритма есть недостатки. При его использовании возможно появление графических артефактов, которые выражаются в виде мерцания ячеек при перемещении виртуальной камеры. Происходит это из-за того, что не хватает точности типа данных для хранения вещественных чисел, применяемого в видеоадаптерах, вследствие чего поочередно выбираются соседние пиксели текстуры. Одним из решений этой проблемы является применение фильтрации к текстуре [7]. В зависимости
от режима фильтрации может вычисляться среднее значение цвета каждой отдельной ячейки на основе соседних ячеек. В данном случае фильтрация неприменима, так как каждый пиксель текстуры должен соответствовать конкретной ячейке геометрии нефтяного пласта, чтобы избежать неправильной закраски. Соответственно, требуется однозначно определить пиксель в текстуре при помощи текстурных координат.
Рассмотрим несколько способов на примере данной модели. Возможно применение формулы для повышения точности определения пикселя:
TC = (0.5 / L) + (N / L), (7)
где N – индекс обрабатываемой ячейки геометрии; L – размер текстуры по заданной оси; TC – значение текстурной координаты по заданной оси.
Однако данный способ недостаточно повышает точность определения для рассматриваемой модели – мерцание сохраняется. Необходимая точность может быть достигнута с использованием формулы
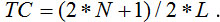 (8)
(8)
Причем расчеты должны проводиться как для U, так и для V оси.
Далее алгоритм повторяется для вершин всех треугольников, в рассматриваемом случае 24 раза.
Заключение
В статье описан метод построения виртуальной трехмерной модели по геологическим данным пласта. Предложено формирование геометрии ячейки пласта с использованием трехмерной модели выпуклого многоугольника с учетом освещения, порядка обработки вершин. Для корректного освещения модели вычисляются нормали для каждой вершины в процессе построения виртуальной сцены. Разработан алгоритм определения текстурных координат, при помощи которого удалось избежать мерцания объектов при отображении путем повышения точности определения пикселя текстуры для каждой ячейки пласта [8]. Представленные алгоритмы и подходы применимы при визуализации данных в современных и перспективных гидродинамических симуляторах.
Работа выполнена при поддержке РФФИ, грант № 16-29-15135.
Литература
1. Каневская Р.Д. Математическое моделирование гидромеханических процессов разработки ме-сторождений углеводородов. М., 2003. 128 с.
2. Захарова А.А., Иванов М.А. Оптимизация процесса цифрового 3D моделирования месторождений нефти и газа // Изв. Томского политех. ун-та. 2008. Т. 312. № 5. C. 119.
3. Каплан И.А. Практические занятия по высшей математике. Харьков: Изд-во Харьков. гос. ун-та, 1974. 194 c.
4. Афанаскин И.В., Родителев А.В., Вольпин С.Г., Гиацинтов А.М., Саитгареев А.Р., Ялов П.В. Опе-ративное моделирование заводнения нефтяных месторождений с учетом влияния законтурной области // Вестн. кибернетики. 2017. С. 108–117.
5. Афанаскин И.В., Ялов П.В., Родителев А.В., Гиацинтов А.М. Решение задач оптимизации
при суперэлементном моделировании разработки нефтяных месторождений // Программные продукты
и системы. 2017. № 3. C. 384–391.
6. Скворцов А.В. Триангуляция Делоне и ее применение. Томск: Изд-во Томск. гос. ун-та, 2002. 128 c.
7. Shreiner D. OpenGL®: Programming guide, 7th ed. Addison-Wesley Publ., 2010, 1018 p.
8. Гаврилов С.С. Трехмерное геологическое моделирование природных резервуаров на основе литолого-фациального анализа (на примере юрских и нижнемеловых отложений Западной Сибири). URL: http://geo.web.ru/db/msg.html?mid=1181203&uri=part01.html (дата обращения: 13.03.2019).
Comments