(Работа выполнена при поддержке РФФИ, гранты №№12-01-0190, 13-01-12402)
Терминология и изложение базисных результатов в данной работе соответствуют [1]. Пусть 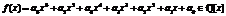 – свободный от квадратов многочлен. Через Jf обозначим якобиан (якобиево многообразие) гиперэллиптической кривой рода 2, определяемой уравнением y2 = f (x), а через
– свободный от квадратов многочлен. Через Jf обозначим якобиан (якобиево многообразие) гиперэллиптической кривой рода 2, определяемой уравнением y2 = f (x), а через 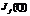 – множество его точек, определенных над
– множество его точек, определенных над 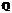 . Уже более 30 лет остается открытой проблема существования такой константы C, что для любого f и любой точки конечного порядка
. Уже более 30 лет остается открытой проблема существования такой константы C, что для любого f и любой точки конечного порядка 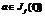 порядок точки a не превосходит C.
порядок точки a не превосходит C.
За это время не были найдены существенные идеи для решения данной проблемы, поэтому усилия исследователей направлены на поиск и построение точек в 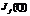 неизвестных ранее конкретных порядков. Начиная с 1990 года рядом математиков (Flynn, Leprevost, Howe, Poonen, Ogawa, Elkies и другими) было доказано существование
неизвестных ранее конкретных порядков. Начиная с 1990 года рядом математиков (Flynn, Leprevost, Howe, Poonen, Ogawa, Elkies и другими) было доказано существование 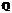 -точек кручения якобианов гиперэллиптических кривых рода 2, определенных над
-точек кручения якобианов гиперэллиптических кривых рода 2, определенных над 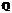 , следующих порядков: 11, 13, 15, 17, 19, 20, 21, 22, 23, 24, 25, 26, 27, 29, 30, 32, 34, 35, 39, 40, 45, 60, 63 (см. [1] и указанную там литературу). Последние найденные
, следующих порядков: 11, 13, 15, 17, 19, 20, 21, 22, 23, 24, 25, 26, 27, 29, 30, 32, 34, 35, 39, 40, 45, 60, 63 (см. [1] и указанную там литературу). Последние найденные 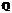 -точки кручения датированы 2000 годом.
-точки кручения датированы 2000 годом.
В серии работ 2009–2010 гг. [2–4] В.П. Платоновым (совместно с В.В. Беняш-Кривецом) была обнаружена глубокая связь между проблемой существования нетривиальных единиц в гиперэллиптических полях с произвольным полем констант, формальными рядами Лорана, ганкелевыми матрицами, непрерывными дробями и проблемой кручения в якобианах. В 2012 г. в работах [5] и [6] В.П. Платонову (совместно с М.М. Петруниным) с помощью новых эффективных алгоритмов и супервычислений удалось завершить доказательство гипотезы Пунена 1996 г. о существовании 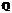 -точек любого порядка £ 30 в Jf для подходящих f, доказать существование
-точек любого порядка £ 30 в Jf для подходящих f, доказать существование 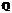 -точек порядков 33, 36 и 48, а также единообразно получить точки кручения всех простых порядков вплоть до 29-го в Jf для подходящих f. В декабре 2012 г. E. Howe указал якобиан, содержащий
-точек порядков 33, 36 и 48, а также единообразно получить точки кручения всех простых порядков вплоть до 29-го в Jf для подходящих f. В декабре 2012 г. E. Howe указал якобиан, содержащий 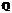 -точку кручения 70-го порядка (см. [1]).
-точку кручения 70-го порядка (см. [1]).
В данной статье описан подход к организации супервычислений, связанных с указанным методом Платонова поиска и построения фундаментальных единиц в гиперэллиптических полях с 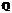 в качестве поля констант. Эти вычисления позволили доказать гипотезу Пунена, а также существование
в качестве поля констант. Эти вычисления позволили доказать гипотезу Пунена, а также существование  -точек кручения новых порядков, упомянутых выше.
-точек кручения новых порядков, упомянутых выше.
Математические аспекты проблемы
Для дальнейшего изложения необходимо вспомнить несколько понятий и фактов (см. [1]).
Обозначим
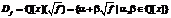 .
.
Элемент u Î Df называется единицей, если u обратим в кольце Df. Степень единицы 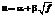 определяется как степень многочлена a(x). Если
определяется как степень многочлена a(x). Если 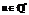 , тогда u называется тривиальной единицей в Df. Предположим, что Df обладает нетривиальными единицами. Тогда мультипликативная группа
, тогда u называется тривиальной единицей в Df. Предположим, что Df обладает нетривиальными единицами. Тогда мультипликативная группа 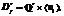 где áu1ñ – бесконечная циклическая группа. Элемент u1 называется фундаментальной единицей в Df.
где áu1ñ – бесконечная циклическая группа. Элемент u1 называется фундаментальной единицей в Df.
В работе [3] отмечено, что существование фундаментальной единицы степени m в кольце Df влечет за собой существование точки кручения степени m в группе 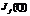 . Этот факт позволяет сосредоточиться на поиске фундаментальных единиц колец Df, так как наличия фундаментальной единицы такого кольца достаточно для существования
. Этот факт позволяет сосредоточиться на поиске фундаментальных единиц колец Df, так как наличия фундаментальной единицы такого кольца достаточно для существования 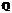 -точки кручения якобиана Jf соответствующего порядка.
-точки кручения якобиана Jf соответствующего порядка.
В работе [4] был доказан критерий существования нетривиальных единиц и предложен алгоритм вычисления фундаментальных единиц над любым полем K, характеристика которого отлична от 2. В случае 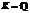 критерий выглядит следующим образом.
критерий выглядит следующим образом.
Без ограничения общности положим a6 = 1 и разложим 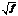 в ряд Лорана:
в ряд Лорана:
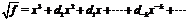 .
.
Рассмотрим матрицу
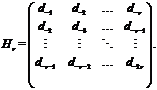
Кольцо Df имеет нетривиальную единицу 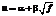 , где
, где 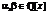 и degb = r тогда и только тогда, когда ранг матрицы Hr +1 меньше, чем r +, и rankHm = m при m < r + 1; при этом degu = r + 3.
и degb = r тогда и только тогда, когда ранг матрицы Hr +1 меньше, чем r +, и rankHm = m при m < r + 1; при этом degu = r + 3.
Чтобы получить целостное представление об алгоритме, опишем в общих чертах этапы проверки наличия фундаментальной единицы в кольце Df степени, не более заданной:
– вычислить достаточное количество коэффициентов разложения 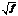 в ряд Лорана;
в ряд Лорана;
– вычислять ранг соответствующей матрицы Hr начиная с r = 1 и до тех пор, пока ранг Hr впервые не станет меньше r; в этом случае в кольце Df существует нетривиальная единица;
– если же rankHr = r для всех r, меньших пороговой величины, то фундаментальной единицы степени, не более заданной, в кольце Df не существует.
Следующий метод поиска фундаментальных единиц в гиперэллиптических полях имеет другую природу и опирается на результаты теории непрерывных дробей.
Пусть
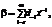
где b – элемент поля формальных степенных рядов с коэффициентами из 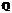 .
.
Положим
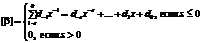
Пусть a0 = [b]. Если b – a0 ¹ 0, положим
Далее по индукции определяем элементы ai, bi: если bi–1 – ai –1 ¹ 0, то
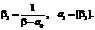
В результате получим непрерывную дробь
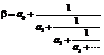
Можно доказать, что кольцо Df обладает нетривиальными единицами тогда и только тогда, когда 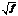 разлагается в периодическую непрерывную дробь.
разлагается в периодическую непрерывную дробь.
Определим по индукции элементы 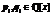 . Положим
. Положим
p –2 = 0, p–1 = 1, q–2 = 1, q–1 = 0
и, если n ³ 0, то
pn = anpn–1 + pn–2, qn = anqn –1 + qn–2.
Положим
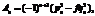
Bn = (–1)n(pnpn–1 – fqnqn–1).
Видим, что, если существуют такие i, j, i < j, что Ai = Aj, Bi = Bj, тогда b разлагается в периодическую непрерывную дробь. Таким образом, учитывая вышесказанное, для доказательства наличия в кольце Df нетривиальной единицы достаточно найти такие номера i, j, i < j, что для соответствующих Ai, Aj, Bi, Bj, полученных из разложения 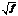 в непрерывную дробь, выполняется соотношение Ai = Aj, Bi = Bj.
в непрерывную дробь, выполняется соотношение Ai = Aj, Bi = Bj.
Сформулируем в общих чертах второй алгоритм проверки кольца Dj на наличие нетривиальных единиц степени, не более заданной:
– вычислить достаточное количество коэффициентов разложения 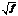 в ряд Лорана;
в ряд Лорана;
– вычислить Ai, Bi для соответствующего i;
– если найдены такие i, j, i ¹ j, что Ai = Aj, Bi = Bj, в кольце Df существует нетривиальная единица;
– если при достижении индексом i пороговой величины все пары Aj, Bj при i < j различны, фундаментальной единицы степени, не более заданной, в кольце Df не существует.
Подробно вышеописанные методы и алгоритмы рассмотрены в работах [1–4].
Вычислительные аспекты проблемы
В подходах, предшествующих подходу Платонова, построение точек конечного порядка над полем рациональных чисел на якобианах гиперэллиптических кривых базировалось на исследовании кривых специального вида, таких как модулярные кривые, либо было основано на процедуре, использующей идеи Серра. Во втором случае получающийся в итоге якобиан оказывался изогенным произведению двух эллиптических кривых. Подход к построению якобиана и вычислению соответствующих точек кручения в нем не был унифицирован и требовал отдельных трудоемких вычислений в каждом конкретном случае.
Помимо этого, в системе компьютерной алгебры Magma реализован алгоритм вычисления группы кручения якобиана заданной кривой, что позволяет осуществить перебор подходящих кривых на предмет наличия нетривиальных 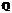 -точек кручения соответствующих якобианов. Названная реализация достаточно громоздка, и скорость перебора составляет около 320 кривых в секунду при задействовании всех ядер двух процессоров Intel Xeon E5-2670.
-точек кручения соответствующих якобианов. Названная реализация достаточно громоздка, и скорость перебора составляет около 320 кривых в секунду при задействовании всех ядер двух процессоров Intel Xeon E5-2670.
Реализация в системе компьютерной алгебры Sage матричной версии алгоритма поиска и построения фундаментальных единиц в кольце Df и, как следствие, поиска точек кручения позволяет достичь скорости перебора около 640 кривых в секунду на тех же процессорах. Отметим, что реализация в системе Sage версии алгоритма, основанной на использовании непрерывных дробей, а также реализация обеих версий алгоритма на языке C с использованием библиотеки GMP для обеспечения поддержки вычислений над полем 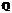 не дали существенного прироста производительности по сравнению с реализацией матричной версии алгоритма в системе Sage.
не дали существенного прироста производительности по сравнению с реализацией матричной версии алгоритма в системе Sage.
К сожалению, прямой перебор многочленов как в системе Magma (прямое вычисление групп кручения), так и с помощью программных реализаций описанных выше алгоритмов (поиск фундаментальных единиц соответствующих гиперэллиптических полей) над полем рациональных чисел 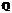 недостаточно эффективен, быстро упирается в вычислительный потолок и не позволяет получать точки кручения новых порядков. Существенная причина невысокой производительности заключается в использовании поля рациональных чисел. Помимо того, что выполнение арифметических операций над полем рациональных чисел сложнее выполнения целочисленных арифметических операций, в ходе работы алгоритма у коэффициентов возникают большие значения числителей и знаменателей, размер которых позволяет разместить их только в нескольких ячейках памяти, что также существенно снижает скорость исполнения.
недостаточно эффективен, быстро упирается в вычислительный потолок и не позволяет получать точки кручения новых порядков. Существенная причина невысокой производительности заключается в использовании поля рациональных чисел. Помимо того, что выполнение арифметических операций над полем рациональных чисел сложнее выполнения целочисленных арифметических операций, в ходе работы алгоритма у коэффициентов возникают большие значения числителей и знаменателей, размер которых позволяет разместить их только в нескольких ячейках памяти, что также существенно снижает скорость исполнения.
В значительной степени уменьшить влияние вышеописанной проблемы возможно путем применения локально-глобального принципа, доказанного в [3]. Ускорения удается добиться редукцией в поле 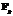 для подходящих простых p. В этом случае происходит естественное сведение задачи поиска фундаментальных единиц кольца Df к задаче поиска фундаментальных единиц кольца
для подходящих простых p. В этом случае происходит естественное сведение задачи поиска фундаментальных единиц кольца Df к задаче поиска фундаментальных единиц кольца 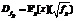 , где fp – многочлен, полученный редукцией f в
, где fp – многочлен, полученный редукцией f в 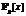 . Для достаточно малых p при использовании
. Для достаточно малых p при использовании 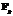 в качестве базового поля все участвующие в вычислении коэффициенты остаются в пределах одной ячейки памяти и в пределах базовых типов используемых языков, что позволяет получить существенный прирост в скорости исполнения по сравнению с вычислениями над полем рациональных чисел.
в качестве базового поля все участвующие в вычислении коэффициенты остаются в пределах одной ячейки памяти и в пределах базовых типов используемых языков, что позволяет получить существенный прирост в скорости исполнения по сравнению с вычислениями над полем рациональных чисел.
Вышесказанное можно проиллюстрировать на следующем примере. Для многочлена f = x6 + x5 + x 4 + x3 + x2 + x + 1 коэффициент d–50 разложения в ряд Лорана имеет вид
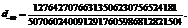
В то же время при редукции в 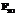 его значение становится следующим:
его значение становится следующим:
d –50 mod251 = 45.
В некотором роде редукция в конечное поле позволяет осуществить фильтрацию многочленов, поступающих на вход алгоритма над полем рациональных чисел. На вход алгоритма, работающего над полем 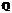 , будут поступать только многочлены, соответствующее кольцо
, будут поступать только многочлены, соответствующее кольцо 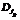 которых обладает фундаментальной единицей нужной степени.
которых обладает фундаментальной единицей нужной степени.
Следующим этапом вычислительного развития описываемого метода стал переход от матричной версии на менее ресурсоемкую версию алгоритма, использующую аппарат непрерывных дробей. Можно показать, что оценка количества операций для поиска фундаментальной единицы кольца Df для заданного f этой версии алгоритма составляет O(n), где n – искомая степень фундаментальной единицы, с константой не более 135.
Применение вышеописанных идей позволяет создать программную реализацию на языке программирования C и избавиться от недостатков, присущих системам компьютерной алгебры и языкам высокого уровня. Совокупный эффект от перехода к операциям в конечном поле, использования аппарата непрерывных дробей и смены языка программирования – прирост скорости более чем на 3 порядка по сравнению с реализацией на Sage для вычислений над 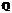 . Для случайного набора кривых время проверки над
. Для случайного набора кривых время проверки над 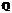 отфильтрованных над конечным полем многочленов оказывается мало по сравнению со временем работы алгоритма фильтрации над
отфильтрованных над конечным полем многочленов оказывается мало по сравнению со временем работы алгоритма фильтрации над 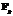 .
.
Для ускорения программной реализации алгоритма поиска фундаментальных единиц в гиперэллиптических полях с конечным полем в качестве поля констант использовался ряд методов оптимизации. В частности, существенный вклад внесло кеширование арифметических операций над конечным полем (сложение, умножение, взятие обратного). На первом этапе работы программы вычислялись таблицы значений для каждой арифметической операции, а на последующих этапах использовалось не прямое вычисление, а обращение к соответствующей таблице, что дало около 45 % прироста скорости.
В силу особенностей аппаратной архитектуры графические ускорители обладают рядом ограничений, что существенно усложняет процесс разработки и отладки, а также значительно повышает требования к алгоритму. Среди ключевых достоинств алгоритмов, связанных с методом Платонова, важно отметить отсутствие рекурсий, малый объем хранимой промежуточной информации, а также хорошие оценки их алгоритмической сложности как в матричном варианте, так и в варианте с привлечением техники непрерывных дробей. Применение локально-глобального принципа, редукция в поле 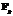 и перечисленные достоинства алгоритма, основанного на использовании аппарата непрерывных дробей, позволили создать параллельную программную реализацию алгоритма, оптимизированную для исполнения в гетерогенных вычислительных системах. Вышеупомянутая реализация основана на открытом стандарте OpenCL и способна исполняться как на центральном процессоре, задействуя все его ядра, так и на графических ускорителях.
и перечисленные достоинства алгоритма, основанного на использовании аппарата непрерывных дробей, позволили создать параллельную программную реализацию алгоритма, оптимизированную для исполнения в гетерогенных вычислительных системах. Вышеупомянутая реализация основана на открытом стандарте OpenCL и способна исполняться как на центральном процессоре, задействуя все его ядра, так и на графических ускорителях.
В качестве аппаратной платформы, на которой производились вычисления, выступает гибридный вычислительный комплекс, собранный в НИИСИ РАН, в составе которого имеются два процессора Intel Xeon E5-2670 и графический ускоритель AMD Radeon HD 7900 Series. На указанном ускорителе на данной задаче удалось достичь более чем восьмикратного ускорения по сравнению c вычислениями на двух процессорах Intel Xeon E5-2670. Помимо указанного оборудования, в распоряжении также находился процессор AMD Opteron Processor 6176SE. Чтобы у читателя сложилась общая картина производительности разработанного алгоритма на различных платформах, приводится сводная таблица скоростей исполнения. В ней сравниваются четыре реализации: на C без кеширования арифметических операций, запущенная ровно на одном ядре процессора (язык C, б/к, одно ядро), на языке C с использованием всех оптимизаций, запущенная на всех ядрах процессоров одновременно (язык C, кеш., все ядра), на C без кеширования арифметических операций, запущенная на всех ядрах одновременно (язык C, б/к, все ядра), и реализация на базе OpenCL, выполненная в силу особенностей графических ускорителей без кеширования (OpenCL, б/к). В ячейках указано количество исследованных кривых в секунду.
Скорость вычисления на различных архитектурах
|
Реализация |
Opteron |
2 ´ Xeon |
Radeon HD7901 |
|
24 ядра |
32 ядра |
– |
|
|
Язык C, б/к, одно ядро |
30200 |
26700 |
– |
|
Язык C, б/к, все ядра |
725000 |
855000 |
– |
|
Язык C, кеш., все ядра |
1050000 |
1200000 |
– |
|
OpenCL, б/к |
600000 |
700000 |
10050000 |
Используя рассматриваемый вычислительный подход для исследования массива кривых {fj} на наличие фундаментальных единиц определенных степеней в кольцах 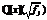 , можно эффективно применить многоступенчатую программную реализацию. На первых двух этапах для некоторых p производится быстрый предварительный отсев многочленов, соответствующие редуцированные кольца
, можно эффективно применить многоступенчатую программную реализацию. На первых двух этапах для некоторых p производится быстрый предварительный отсев многочленов, соответствующие редуцированные кольца 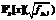 которых не обладают фундаментальными единицами искомых степеней. На третьем, заключительном, этапе значительно уменьшенный на предшествующих этапах массив кривых поступает на вход алгоритма, работающего над
которых не обладают фундаментальными единицами искомых степеней. На третьем, заключительном, этапе значительно уменьшенный на предшествующих этапах массив кривых поступает на вход алгоритма, работающего над 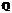 , что позволяет на выходе получить искомые кривые из первоначального массива. Правильно подобрав набор простых pi, можно утверждать, что с высокой вероятностью массив, отфильтрованный с помощью редукций к соответствующим
, что позволяет на выходе получить искомые кривые из первоначального массива. Правильно подобрав набор простых pi, можно утверждать, что с высокой вероятностью массив, отфильтрованный с помощью редукций к соответствующим 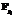 , будет полностью состоять из кривых, чьи кольца
, будет полностью состоять из кривых, чьи кольца 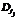 будут обладать фундаментальными единицами искомых степеней. Для случайно выбранного массива кривых при правильно подобранных pi время исполнения последнего этапа пренебрежимо мало по сравнению со временем исполнения первых двух этапов, когда вычисления осущствляются над полями
будут обладать фундаментальными единицами искомых степеней. Для случайно выбранного массива кривых при правильно подобранных pi время исполнения последнего этапа пренебрежимо мало по сравнению со временем исполнения первых двух этапов, когда вычисления осущствляются над полями 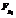 .
.
Описанная многоступенчатая реализация также была разработана с использованием стандарта OpenCL для вышеуказанного вычислительного комплекса, причем удалось одновременно задействовать как центральные процессоры, так и графические ускорители.
Более подробно опишем первые два этапа. Напомним, что для произвольного многочлена 6-й степени 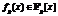 , свободного от квадратов, соответствующее кольцо
, свободного от квадратов, соответствующее кольцо 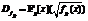 всегда обладает нетривиальными единицами. Основного ускорения удается достичь за счет предварительного вычисления фундаментальных единиц ограниченной степени всех многочленов 6-й степени в
всегда обладает нетривиальными единицами. Основного ускорения удается достичь за счет предварительного вычисления фундаментальных единиц ограниченной степени всех многочленов 6-й степени в 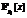 для малых простых pi. Вычисленные единицы помещались в соответствующие таблицы и сохранялись на жестком диске.
для малых простых pi. Вычисленные единицы помещались в соответствующие таблицы и сохранялись на жестком диске.
Очевидно, что всякому многочлену 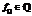 , соответствующее кольцо
, соответствующее кольцо 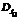 которого обладает фундаментальной единицей степени n, можно сопоставить многочлен
которого обладает фундаментальной единицей степени n, можно сопоставить многочлен 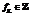 , соответствующее кольцо
, соответствующее кольцо 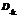 которого обладает фундаментальной единицей степени n. На первом этапе для каждого многочлена
которого обладает фундаментальной единицей степени n. На первом этапе для каждого многочлена  , соответствующее кольцо
, соответствующее кольцо 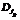 которого обладало фундаментальной единицей заданной степени, вычислялись все многочлены
которого обладало фундаментальной единицей заданной степени, вычислялись все многочлены 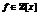 , коэффициенты которых попадали в определенный диапазон и при этом совпадали с соответствующими коэффициентами fp при редукции в поле
, коэффициенты которых попадали в определенный диапазон и при этом совпадали с соответствующими коэффициентами fp при редукции в поле 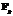 . Далее, на втором этапе, эти многочлены редуцировались по нескольким различным простым pj и отсеивались те многочлены, соответствующие редуцированные кольца
. Далее, на втором этапе, эти многочлены редуцировались по нескольким различным простым pj и отсеивались те многочлены, соответствующие редуцированные кольца 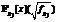 которых не обладают фундаментальными единицами искомых степеней. Для получения дополнительного ускорения отсеивание также происходило путем сопоставления редуцированного многочлена и заранее вычисленной степени единицы, сохраненной в таблице.
которых не обладают фундаментальными единицами искомых степеней. Для получения дополнительного ускорения отсеивание также происходило путем сопоставления редуцированного многочлена и заранее вычисленной степени единицы, сохраненной в таблице.
Используя свойства гиперэллиптических кривых, удается сократить количество многочленов в Fp[x], в соответствующих кольцах которых вычисляются фундаментальные единицы. Как следствие, без ограничения общности удается уменьшить количество предварительно найденных многочленов, что позволяет, с одной стороны, сократить перебор, а с другой – увеличить простые p, для которых составляются упомянутые выше таблицы, что гарантирует дополнительное ускорение. Так, увеличение на предварительном этапе простого p в два раза влечет четырехкратное ускорение нахождения всех фундаментальных единиц ограниченной степени колец для 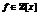 , коэффициенты которых ограничены константой C.
, коэффициенты которых ограничены константой C.
За счет оптимизаций на всех трех этапах выполнения удалось достичь скорости исполнения, более чем на четыре порядка превышающей скорость выполнения упомянутой ранее одноступенчатой OpenCL-реализации.
Таким образом, в результате перехода к алгоритму, использующему аппарат непрерывных дробей, многоступенчатой фильтрации путем редукции в соответствующие 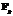 и применения многочисленных математических и вычислительных оптимизаций алгоритма удалось достичь скорости перебора кривых более чем на девять порядков выше, чем при использовании реализации над
и применения многочисленных математических и вычислительных оптимизаций алгоритма удалось достичь скорости перебора кривых более чем на девять порядков выше, чем при использовании реализации над 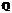 или реализации алгоритма поиска точек кручения на основе системы компьютерной алгебры Magma, что позволило доказать существование точек кручения новых порядков, указанных во введении к настоящей статье.
или реализации алгоритма поиска точек кручения на основе системы компьютерной алгебры Magma, что позволило доказать существование точек кручения новых порядков, указанных во введении к настоящей статье.
Автор благодарит сотрудников НИИСИ РАН Малого А.А. и Богданова П.Б. за консультации и помощь, оказанную в процессе разработки программных реализаций, описанных в настоящей статье.
Литература
1. Платонов В.П. Теоретико-числовые свойства гиперэллиптических полей и проблема кручения в якобианах гиперэллиптических кривых над полем рациональных чисел // Успехи матем. наук. 2014. Т. 69. № 1. С. 3–38.
2. Беняш-Кривец В.В., Платонов В.П. Группы S-единиц в гиперэллиптических полях и непрерывные дроби // Математический сборник. 2009. Т. 200. № 11. С. 15–44.
3. Платонов В.П. Арифметика квадратичных полей и кручение в якобианах // Доклады РАН. 2010. Т. 430. № 3. С. 318–320.
4. Беняш-Кривец В.В., Платонов В.П. О новом локально-глобальном принципе для квадратичных функциональных полей // Доклады РАН. 2010. Т. 433. № 2. С. 154–157.
5. Платонов В.П., Петрунин М.М. Новые порядки точек кручения в якобианах кривых рода 2 над полем рациональных чисел // Доклады РАН. 2012. Т. 443. № 6. С. 664–667.
6. Платонов В.П., Петрунин М.М. О проблеме кручения в якобианах кривых рода 2 над полем рациональных чисел // Доклады РАН. 2012. Т. 446. № 3. С. 263–264.
7. Stein W.A. et al. Sage Mathematics Software. The Sage Development Team. URL: http://www.sage-
math.org (дата обращения: 1.07.2014).
8. Bosma W., Cannon J. J., Fieker C., Steel A. (eds.). Handbook of Magma functions, Edition 2.16 (2010), 5017 p.
9. Khronos Group, Open Computing Language (OpenCL)/ URL: https://www.khronos.org/opencl/ (дата обращения: 1.07.2014).
Comments