Работа с многомерными данными большой размерности является крайне востребованной во многих областях, таких как мультимедийные БД, системы проектирования, молекулярная биология, интеллектуальные системы, обработка изображений, поисковые системы и т.д. Для работы с ними разработано множество структур данных, таких как R-дерево, R*-дерево, S-дерево, хеширование PLOP, MOLHPE и др. [1–4]. Однако до сих пор существует множество проблем, связанных с недостаточной проработкой алгоритмов и их исследованием в разных ситуациях. Одна из хорошо известных проблем заключается в том, что при увеличении размерности данных большинство структур начинают терять производительность [5–8]. Подходы, заложенные в X-дерево, призваны в числе прочих сгладить негативные последствия данной проблемы.
Структура Х-дерева относится к семейству R-подобных деревьев. R-дерево разбивает многомерное пространство на множество иерархически вложенных и, возможно, пересекающихся прямоугольников (для двухмерного пространства) [9]. В случае трехмерного или многомерного пространства это будут прямоугольные параллелепипеды (кубоиды) или параллелотопы. Алгоритмы вставки и удаления используют эти ограничивающие прямоугольники для обеспечения того, чтобы близкорасположенные объекты были помещены в одну листовую вершину. Однако Х-дерево имеет одно важное отличие от других структур – комбинирование одновременно линейных и иерархических принципов для индексирования данных с целью увеличения производительности индекса в пространствах большой размерности, в которых достаточно сложно эффективно сгруппировать объекты на слабо пересекающиеся области. Общий принцип и описание метода представлены в [10]. В данной работе сделана попытка детализировать алгоритмы построения и обработки Х-дерева вплоть до подробных блок-схем, достаточных для реализации на любом алгоритмическом языке.
Принцип индексирования данных в X-дереве
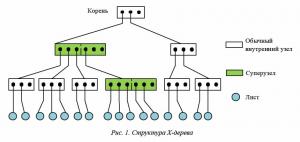
Структура X-дерева во многом схожа со структурой R-дерева, от которого оно и была образована. Однако оригинальное R-дерево не очень хорошо подходит для индексирования данных в пространствах большой размерности. Это связано с тем, что в таких пространствах велика вероятность получения внутренних узлов дерева с большим процентом перекрытия, что приводит к значительному снижению производительности. Поэтому в X-дерево добавлены два новых принципа, которые и обусловливают его отличия от оригинальной структуры (рис. 1).
1. Суперузлы. В ряде случаев вместо R-дерева c большими областями пересечения эффективнее использовать линейную структуру данных. X-дерево комбинирует линейный и иерархический способы хранения информации, используя первый только там, где невозможно разделить узлы без образования пересечений. Если выполнить деление узла невозможно, его размер увеличивается (он превращается в так называемый суперузел, внутри которого используется линейный способ поиска).
2. Деление с минимальной областью пересечения. Для того, чтобы можно было эффективнее производить деление узлов, в X-дереве сохраняется история подобных операций для определения наиболее предпочтительной оси пространства. Это позволяет в дальнейшем более обоснованно выбирать ось, по которой можно выполнить деление с образованием минимальной области пересечения.
Рассмотрим структуру дерева более подробно. В отличие от R-дерева после построения X-дерево может содержать два типа узлов – обычные и суперузлы.
Обычные узлы – узлы нормального размера, полностью аналогичные узлам обычного R-дерева и содержащие массив минимальных ограничивающих прямоугольников потомков (MBR) и файловые указатели на потомков. Однако у внутренних узлов и листовых узлов есть одно отличие. Внутренние узлы также хранят историю деления своих потомков. Листья такой истории не содержат, но, как и внутренние узлы, могут образовывать суперузлы.
Суперузлы – узлы произвольного размера, кратного размеру обычного узла. Эти узлы не подвержены правилу на максимальное количество объектов в них, как в оригинальном R-дереве. В остальном же они подобны обычным узлам.
Алгоритм добавления объектов в дерево
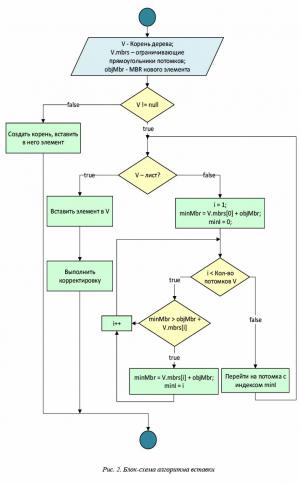
Добавление нового объекта в дерево начинается с поиска подходящего листового узла в нем. Для этого в дереве производится рекурсивный поиск места вставки от корня к листовому уровню. Для каждого обрабатываемого узла просматриваются MBR всех его потомков и выбирается тот узел, вставка в который приведет к минимальному увеличению объема MBR. После вставки элемента производится корректировка дерева. Как можно видеть из описания, на этом этапе алгоритм добавления ничем не отличается от аналогичного алгоритма для оригинального R-дерева. Все основные нюансы сосредоточены в алгоритмах корректировки дерева и деления узла, рассмотренных далее. Полная блок-схема алгоритма добавления показана на рисунке 2.
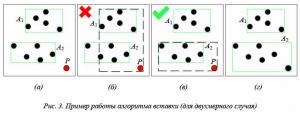
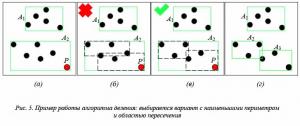
Пример работы алгоритма для двухмерного случая показан на рисунке 3. Пусть имеется некоторое дерево, состоящее из двух узлов A1 и A2, объединяющих по 5 элементов (рис. 3а), в него мы добавляем новый объект P. Данный объект не вписывается ни в один узел и просто так добавить его, как показано на рисунке 3б, нельзя. Для определения претендента на вставку происходит проход по дереву от корня к листьям (в рассматриваемом случае это A1 и A 2) и проверка, насколько MBR каждого из них увеличится в случае вставки в него объекта P. Минимальное увеличение произойдет в узле A2, именно поэтому он и выбирается для размещения P (см. рис. 3в). После всех операций добавления результирующее дерево и деление пространства будут иметь вид, представленный на рисунке 3г.
Алгоритм корректировки дерева
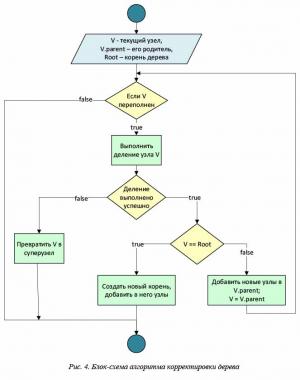
После размещения нового объекта в листовом узле дерева необходимо произвести его корректировку. Для этого проверяется переполненность узла (максимальное заполнение узла объектами) и в случае необходимости производится его деление. Если невозможно разделить узел так, чтобы область пересечения новых узлов не превышала заданный минимум, его нужно заменить на суперузел (или увеличить его размер, если вершина уже является суперузлом). Процедура распространяется вверх по дереву от листа до корня. В случае необходимости деления корня образуется новая вершина и высота дерева увеличивается. Таким образом, дерево растет вверх и всегда остается идеально сбалансированным. Блок-схема алгоритма корректировки показана на рисунке 4.
Алгоритм деления узла
Смысл операции разделения узлов состоит в том, чтобы разбить переполненный узел на два новых с минимальным взаимным пересечением полученных узлов. Пример разделения узла на части продемонстрирован на рисунке. Слева показана исходная ситуация. После добавления объекта P узел A2 стал переполненным и его необходимо разбить на две части. Можно предложить два варианта разбиения, показанные на рисунках 5б и 5в. Однако вариант, изображенный на рисунке 5в, более предпочтителен, так как взаимное пересечение образованных частей в нем гораздо меньше. Результат разбиения показан на рисунке 5г.
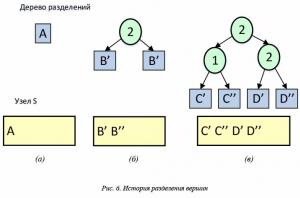
Для нахождения оптимального разделения узла на части в X-деревьях хранится и используется история деления узлов. Если все потомки данного узла были разделены по какой-либо одной оси, то для получения минимальной области пересечения необходимо разделять этот узел по той же самой оси. Для удобства историю делений можно представить в виде бинарного дерева (рис. 6).
Пусть в начальный период дерево состояло из одной вершины A (рис. 6а). Допустим, после серий добавлений появилась необходимость разделения этой вершины на две новые – B' и B''. Если такое деление происходило по второму измерению, дерево разделений будет иметь вид, показанный на рисунке 6б. Допустим, в дальнейшем вершина B' разделилась по первому измерению на C' и C'', а вершина B'' – по второму измерению на D' и D''. Тогда итоговое дерево делений будет иметь вид, показанный на рисунке 6в.
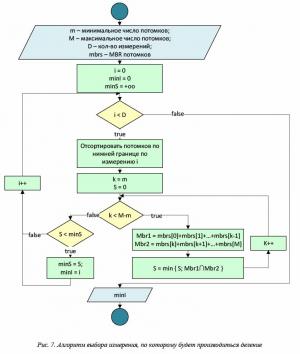
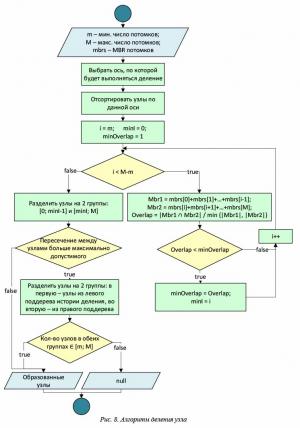
Чтобы структура X-дерева оставалась эффективной для данных небольшой размерности (d = 2, 3), при делении сначала применяется алгоритм разделения на основе геометрических данных (например, алгоритм разделения R*-деревьев), и, если он создает узлы с большим пересечением, используется описанный выше метод. Блок-схема этого алгоритма представлена на рисунках 7 и 8.
Алгоритм удаления элемента из дерева
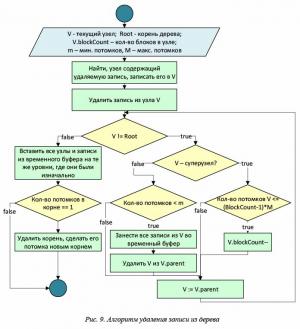
Еще одной важной процедурой является удаление объекта из дерева (рис. 9). При удалении сначала происходит поиск листовой вершины, в которой находится данный объект, и этот объект удаляется из нее. После удаления записи количество элементов в вершине может оказаться ниже допустимого минимума. Тогда узел необходимо удалить, а его элементы поместить во временный буфер. После того, как все незаполненные узлы удалены, элементы из буфера снова вставляются в дерево. Процедура вставки в этом случае отличается только тем, что вершины должны быть добавлены на тот же уровень, на котором они находились раньше, чтобы дерево осталось сбалансированным.
Следует учитывать, что в процессе удаления могут появиться суперузлы с пустыми блоками. В этом случае их размер уменьшается на один блок или они заменяются обычным узлом, если их размер становится допустимым для этого. Блок-схема алгоритма удаления показана на рисунке 9.
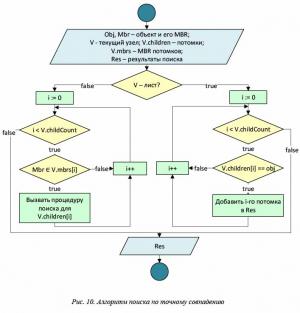
Алгоритм поиска по точному совпадению
Поиск в X-дереве полностью аналогичен поиску в R-дереве. Процедура начинается с корня дерева. В рассматриваемом узле определяются все потомки, MBR которых содержит заданный элемент. Для каждого потомка рекурсивно вызывается эта же процедура. В случае, если текущий узел – лист, все его записи, совпадающие с заданным MBR, добавляются в результаты поиска. Блок-схема алгоритма поиска показана на рисунке 10, а пример выполнения для двухмерного случая – на рисунке 11.
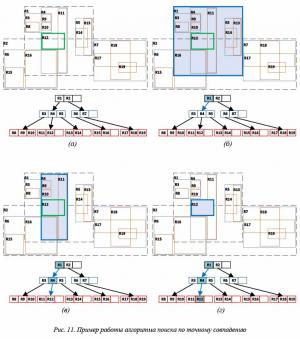
На рисунке 11 показан пример выполнения алгоритма поиска. Исходная ситуация представлена
на рисунке 11а. Для примера показан поиск объекта R12.
Алгоритм поиска начинается в корне дерева. В нем перебираются все дочерние вершины и сравнивается, может ли их MBR полностью содержать MBR объекта R12. Среди потомков корневой вершины только R 1 подходит под данное условие (см. рис. 11б), поэтому процедура рекурсивно вызывается именно для него.
Алгоритм поиска начинается в корне дерева. В нем перебираются все дочерние вершины и сравнивается, может ли их MBR полностью содержать MBR объектаR12. Среди потомков корневой вершины только R 1 подходит под данное условие (см. рис. 11б), поэтому процедура рекурсивно вызывается именно для него.
На втором шаге аналогичная проверка происходит для потомков вершины R1 (рис. 11в). В нем заданному условию удовлетворяет только узел R4. Поскольку R4 – это листовая вершина дерева, на последнем этапе происходят сравнение всех ее потомков с объектом поиска R12 и поиск заданного элемента
(рис. 11г).
Заключение
Одной из перспективных структур индексирования многомерных объектов является X-дерево. Однако в литературе на данный момент оно еще мало освещено. В данной работе сделана попытка разобрать все алгоритмы работы с данной структурой, детализировать их до уровня подробных блок-схем, показать примеры и особенности реализации, достаточные для реализации на любом алгоритмическом языке. Особое внимание уделено основным алгоритмам построения, таким как вставка объекта, корректировка, деление узла. Данная работа будет интересна всем, кто заинтересован в развитии и исследованиях в области многомерных данных.
Литература
1 . Sapino M.L., Candan K.S. Data management for multimedia retrieval. Cambridge Univ. Press, 2010, 473 p.
2 . Samet H. Foundations of multidimensional and metric data structures. Morgan Kaufmann Publ., 2006, 993 p.
3 . Гулаков В.К., Трубаков А.О., Трубаков Е.О. Структуры и алгоритмы обработки многомерных данных. СПб: Лань, 2018. 356 с.
4 . Mokbel M.F., Ghanem T.M., Aref W.G. Spatio-temporal access methods. IEEE Data Eng. Bull., 2003, no. 26, vol. 2, pp. 40–49.
5 . Moënne-Loccoz N. High-dimensional access methods for efficient similarity queries. Tech. Report 05.05. Univ. of Geneva, 2005.
6 . Yufei Tao, Ke Yi, Cheng Sheng, Panos Kalnis. Efficient and accurate nearest neighbor and closest pair search in high-dimensional space. ACM TODS, 2010, pp. 1–46.
7 . Chunyang Ma, Yongluan Zhou, Lidan Shou, Dan Dai, Gang Chen. Matching query processing in high-dimensional space. Proc. 20th ACM Intern. Conf. on Information and Knowledge Management. 2011,
pp. 1589–1594.
8 . Гулаков В.К., Трубаков А.О. Проблема большого объема векторов характеристик в задаче многомерного индексирования графической информации // Изв. Волгоград. гос. технич. ун-та. 2010. № 11. С. 133–137.
9 . Beckmann N., Kriegel H.P., Schneider R., Seeger B. The R*-tree: an efficient and robust access method for points and rectangles. Proc. 1990 ACM SIGMOD Intern. Conf. on Management of data, 1990, pp. 322–331.
10 . Berchtold S., Keim D.A., Kriegel H.P. The X-tree: An Index Structure for High-Dimensional Data // Proceedings of the Twenty-second International Conference on Very Large Data-Bases, 1996, pp. 28–39.
Comments