Важное место в современной комбинаторной оптимизации занимают задачи раскроя-упаковки (ЗРУ), привлекая внимание многих ученых как в России, так и за рубежом [1, 2]. Интерес к ЗРУ объясняется, в частности, их большой практической значимостью. Как правило, приложения этих задач относятся к материалоемким производствам, где одним из основных факторов снижения себестоимости выпускаемой продукции является рациональное использование ресурсов.
Существует множество разновидностей этой задачи: двумерная упаковка, двумерная упаковка в полуограниченную полосу,линейная упаковка,упаковка по весу, упаковка по стоимости и другие. Задачи упаковки могут применяться в области оптимального заполнения контейнеров, загрузки грузовиков с ограничением по весу, созданием резервных копий на съемных носителях и т.д. На сегодняшний день для решения ЗРУ используются различные оптимизационные алгоритмы [3–6].
В работе рассматривается задача упаковки полуограниченной полосы (1.5 Dimensional Bin Packing, 1.5DBP). Термин 1.5D ввел в 1980 г. A. Hinxman. Задан набор прямоугольников. Дан один большой объект (называемый полосой), чья ширина W задана, а длина L – искомое значение переменной. Цель состоит в том, чтобы минимизировать длину L полосы, содержащей прямоугольники, помещенные в полосу без их взаимного перекрытия.
Известно, что ЗРУ относятся к классу NP-трудных задач комбинаторной оптимизации. Для их решения российскими и зарубежными учеными разработано большое количество методов и алгоритмов, различающихся как областью применения, так и эксплуатационными свойствами. Методы решения ЗРУ принято разделять на две большие группы: точные и приближенные. Поскольку точные методы не позволяют решать задачи упаковки большой размерности за полиномиальное время, во многих работах большое внимание уделяется разработке приближенных и эвристических методов [3–11]. Приближенные методы не гарантируют нахождения глобального оптимума ЗРУ и ориентированы на получение некоторого приемлемого или допустимого решения [8–11]. Для практических задач значимая потеря точности не всегда является приемлемой. В связи с этим большое значение приобретают разработка и исследование методов решения ЗРУ, в том числе и методов локального поиска, обеспечивающих высокое качество решения. Результатом непрекращающегося поиска наиболее эффективных методов упаковки стало использование бионических методов и алгоритмов. Одним из новых направлений таких методов являются мультиагентные методы интеллектуальной оптимизации, базирующиеся на моделировании коллективного интеллекта биологических систем [12]. К таким методам можно отнести генетические и роевые алгоритмы [12–14]. В работе излагается метод решения задачи упаковки полуограниченной полосы, основанный на моделях роевого интеллекта.
Постановка задачи
Задача прямоугольной упаковки в полосу (1.5 Dimensional Bin Packing, 1.5DBP) состоит в следующем. Исходная информация задается набором данных:H – ширина полубесконечной полосы; R = { ri|i=1, 2, …, m} – набор прямоугольников, где m – количество прямоугольников; W = {wi|i=1, 2, …, m} – вектор ширины прямоугольников; L = {li|i=1, 2, …, m} – вектор длин прямоугольников. Вводится прямоугольная система координат XOY, у которой оси OX и OY совпадают, соответственно, с нижней неограниченной и боковой сторонами полосы. Решение задачи представляется в виде набора элементов <X, Y>, где X = {xi|i=1, 2, …, m), Y={yi|i=1, 2, …, m) – векторы координат прямоугольников. (хi, уi) – координаты нижнего левого угла прямоугольника, соответственно, по оси OX и OY. Набор элементов <X, Y> называется допустимой прямоугольной упаковкой, если выполнены следующие условия:
– стороны прямоугольников параллельны граням полосы;
– прямоугольники не перекрывают друг друга;
– прямоугольники не выходят за границы полосы.
Анализ существующих методов и алгоритмов упаковки в блоки [1–11] показал, что в их основе лежит процедура упорядочения исходного списка элементов, последовательно распределяемых по блокам. Другими словами, в качестве структуры данных, несущих информацию об упаковке, чаще всего используется последовательность номеров прямоугольников, представляющая порядок их укладки, которая называется приоритетным списком. Приоритетный список – это кодированное решение, в терминах
генетического алгоритма – хромосома. Приоритетный список является косвенной схемой кодирования решения. Фактически приоритетный список является интерпретацией решения. Существенную роль в общем процессе нахождения решения играет декодер. Переход от приоритетного списка к решению производится с помощью декодера. Декодер – оператор, осуществляющий укладку прямоугольников по заложенным в нем правилам, позволяющий перейти от косвенной (числовой) схемы кодирования решения задачи к фенотипу.
Важной характеристикой декодера является его способность получить оптимальную упаковку по заранее известному оптимальному коду (приоритетному списку), то есть способность правильно декодировать.
Исходя из вышеизложенного, представляет интерес разработка новых поисковых алгоритмов для решения ЗРУ на базе эффективных метаэвристик формирования приоритетных списков и принципов их декодирования.
Оператор декодирования
Декодер – оператор, позволяющий перейти от косвенной (числовой) схемы кодирования решения задачи к прямой (графической) схеме, он формирует карту раскроя по приоритетному списку. Таким образом, с помощью декодера можно получить координаты прямоугольников, а значит, и графическое представление решения задачи, а также вычислить значение функции пригодности.
Большинство разработанных к настоящему времени декодеров для задачи упаковки в полосу, основанных на эвристических правилах, делятся на три группы: уровневые, шельфовые, плоские.
Плоские алгоритмы размещают прямоугольники строго вплотную друг к другу.
Шельфовые рассматривают сразу несколько шельфов (полок) и распределяют по ним прямоугольники.
Подход всех уровневых алгоритмов заключается в том, что полоса разделяется на уровни, исходя из высоты имеющихся на данном этапе прямоугольников. Прямоугольники размещаются вдоль основания текущего уровня слева направо, пока это возможно; прямоугольник, который не поместился, упаковывается на следующий уровень. Высота каждого уровня определяется по самому высокому прямоугольнику в нем. Прямоугольники, расположенные на одном уровне, образуют ряд. Представим три варианта упаковки [5]:
Next fit level – открывается следующий уровень, предыдущий закрывается, и его больше не рассматриваем;
First fit level – на каждом шаге алгоритма просматривается каждый уровень, начиная с самого нижнего, и прямоугольник упаковывается на первый подходящий, на котором достаточно места;
Best fit level – на каждом шаге алгоритма просматриваются все уровни и выбирается наиболее подходящий – тот, на котором после упаковки останется минимум места.
Модификацией алгоритма Best fit level является алгоритм Floor ceiling no rotation (FCNR). Упаковка осуществляется блоками. Каждый блок ограничен двумя уровнями. Нижний уровень блока – «пол», верхний уровень блока – «потолок». Пока есть возможность, прямоугольники пакуются на «пол» слева направо. Когда место заканчивается, предпринимается попытка упаковать на «потолок» справа налево; если нет места на потолке, то только тогда начинается формирование нового блока. В соответствии с эвристикой BFDH на каждом шаге просматриваются все уровни – сначала «пол», затем «потолок» – на наличие наиболее подходящего места. Метод удачно упаковывает по «потолкам» самые мелкие прямоугольники.
В работе в качестве базовой структуры декодера выбрана эвристика FCNR. Для построения декодера и кодовой последовательности использованы модификации эвристики FCNR и метаэвристики, базирующиеся на моделировании адаптивного поведения биологических систем.
На первом этапе формируется код решения – приоритетный список прямоугольников.
На втором этапе оператором декодирования производится в соответствии с эвристикой «пол–потолок» последовательное заполнение блоков начиная с первого. При заполнении блока сначала заполняется нижний уровень, а затем верхний. Заполнение уровней производится в порядке с приоритетной последовательностью, полученной на первом этапе.
На третьем этапе в каждом блоке прямоугольники сортируются по невозрастанию высоты: на уровне «пол» слева направо; на уровне «потолок» справа налево.
На четвертом этапе заполненные уровни в каждом блоке сближаются на минимально допустимое расстояние, исключающее наложение прямоугольников.
На пятом этапе путем парных перестановок прямоугольников осуществляется сжатие блоков (дополнительное сближение верхнего и нижнего уровней блока). На заключительном этапе производится сжатие по оси OX и определяется размер заполненной части полосы – LR.
Гибридный алгоритм решения задачи упаковки в полуограниченную полосу
Для решения ЗРУ предлагается композитная архитектура многоагентной системы бионического поиска на основе интеграции роевого интеллекта и генетической эволюции [15, 16].
В гибридных алгоритмах преимущества одного алгоритма могут компенсировать недостатки другого. Интеграция метаэвристик популяционных алгоритмов обеспечивает более широкий обзор пространства поиска и более высокую вероятность локализации глобального экстремума задачи. Такой подход позволит частично решить проблему преждевременной сходимости, обеспечит выход из локальных оптимумов и повысит скорость получения результата.
В работе используется низкоуровневая гибридизация вложением, предполагающая сращивание гибридизируемых алгоритмов.
Первый и наиболее простой подход к гибридизации заключается в следующем. Сначала поиск решения осуществляется генетическим алгоритмом [16 ]. Затем на основе популяции, полученной на последней итерации генетического поиска, формируется популяция для роевого алгоритма. В формируемую популяцию включаются лучшие, но отличные друг от друга хромосомы. При необходимости полученная популяция доукомплектовывается новыми индивидами. После этого дальнейший поиск решения осуществляется роевым алгоритмом.
При втором подходе метод роя частиц используется в процессе генетического поиска и играет роль, аналогичную генетическим операторам. В этом случае на каждой итерации генетического алгоритма синтез новых хромосом, с одной стороны, осуществляется с помощью кроссинговера и мутации, а с другой – с помощью операторов направленной мутации метода роя частиц.
Связующим звеном такого подхода является структура данных, описывающая в виде хромосомы решение задачи [17]. Предлагается подход к построению модифицированной парадигмы роя частиц, обеспечивающей возможность одновременного использования хромосом с целочисленными значениями параметров в генетическом алгоритме и в алгоритме на основе роя частиц.
Метод роя частиц (particle swarm optimization, PSO) является методом стохастической оптимизации, в чем-то схожим с эволюционными алгоритмами. Этот метод моделирует не эволюцию, а ройное и стайное поведение животных [6]. В отличие от популяционных методов PSO работает с одной статической популяцией, члены которой постепенно улучшаются с появлением информации о пространстве поиска. Данный метод представляет собой вид направленной мутации (directed mutation). Решения в PSO мутируют в направлении наилучших найденных решений. Частицы никогда не умирают (так как нет селекции).
Рассмотрим каноническую парадигму метода PSO, разработанную Д. Кеннеди и Р. Эберхартом [13]. Метод PSO работает в многомерных, вещественных, метрических пространствах. Многомерное пространство поиска населяется роем частиц [14]. Каждой частице соответствует некоторое решение, определяемое позицией в пространстве решений. Основу поведения роя P = { pi|i=1, 2, …, n} частиц составляет самоорганизация, обеспечивающая достижение общих целей роя на основе низкоуровневого взаимодействия. Каждая частица pi размещается в позиции xi многомерного пространства поиска, связана и может взаимодействовать со всеми частицами роя, она тяготеет к лучшему решению роя. Процесс поиска решений итерационный и заключается в перемещении частиц на каждой итерации в новые позиции.
По аналогии с эволюционными стратегиями рой частиц можно трактовать как популяцию, а частицу как индивида. Это дает возможность построения гибридной структуры поиска решения, основанного на сочетании генетического поиска с методами роя частиц [16, 18]. Связующим звеном такого подхода является структура данных, описывающая решение задачи. В генетических алгоритмах генотип решения представляется в виде хромосомы. При решении комбинаторных задач гены в хромосомах имеют, как правило, дискретные, целочисленные значения. Положение частицы в пространстве поиска является эквивалентом генотипа в эволюционных алгоритмах. Если в качестве описания состояния частицы используется хромосома, то число параметров, определяющих положение частицы в пространстве решений, должно быть равным числу генов в хромосоме. Значение каждого гена откладывается на соответствующей оси пространства решений. В этом случае возникают некоторые требования к структуре хромосомы, значениям генов и пространству поиска.
Каноническая парадигма роя частиц предусматривает использование вещественных значений параметров в многомерных, вещественных, метрических пространствах. Однако в большинстве генетических алгоритмов гены в хромосомах имеют дискретные, целочисленные значения. В свою очередь, хромосомы являются некоторыми интерпретациями решений, которые трансформируются в решения путем декодирования хромосом.
В отличие от канонической парадигмы роя частиц гибридные алгоритмы в качестве моделей для представления решений используют широкий диапазон графовых структур (маршрут, дерево, двудольный граф, паросочетание, внутренне устойчивое множество и т.д.) [8–11]. Это не позволяет напрямую использовать каноническую парадигму роя частиц (например, задача направленной мутации одного дерева в направлении другого, с формальной точки зрения, является весьма нетривиальной).
В связи с этим актуальной является разработка модернизированной структуры пространства поиска, структуры данных для представления решений и позиций, модернизированных механизмов перемещения частиц в пространстве поиска. Исследования показали, что структуры данных для представления позиций и механизмы перемещения частиц в пространстве поиска связаны, но зависят от структуры данных для представления интерпретаций решений.
В работе предлагается подход к построению модифицированной парадигмы роя частиц, обеспечивающей возможность одновременного использования хромосом с дискретными целочисленными значениями параметров в генетическом алгоритме и в алгоритме на основе роя частиц.
Аффинное пространство поиска
Пусть имеется линейное векторное пространство (ЛВП), элементами которого являются n-мерные точки. Каждым любым двум точкам p и q этого пространства однозначным образом сопоставим единственную упорядоченную пару этих точек, которую в дальнейшем будем называть геометрическим вектором (вектором):
p, q ∈ V(p, q) – геометрический вектор (упорядоченная пара).
Совокупность всех точек ЛВП, пополненная геометрическими векторами, называют точечно-векторным, или аффинным пространством. Аффинное пространство является n-мерным, если соответствующее ЛВП также является n-мерным.
Аффинно-релаксационная модель (АРМ) роя частиц – это граф, вершины которого соответствуют позициям роя частиц, а дуги аффинным связям между позициями (точками) в аффинном пространстве. Аффинность – мера близости двух агентов (частиц). На каждой итерации каждый агент pi переходит в аффинном пространстве в новое состояние (позицию), при котором вес аффинной связи между агентом pi и базовым (лучшим) агентом p* уменьшается. Переход агентаpi в новую позицию xi( t+1) из xi(t) осуществляется с помощью релаксационной процедуры.
Специальная релаксационная процедура перехода зависит от вида структуры данных (хромосомы): вектор, матрица, дерево и их совокупности, являющейся интерпретацией решений.
Лучшие частицы (и их позиции) с точки зрения целевой функции объявляются центром притяжения. Векторы перемещения всех частиц в аффинном пространстве устремляются к этим центрам.
Переход возможен с учетом степени близости к одному базовому элементу либо к группе соседних элементов и с учетом вероятности перехода в новое состояние.
Каждую хромосому, описывающую i-е решение популяции, обозначим какHi(t)={gil|l=1, 2, …, n}. Позиция xi(t) соответствует решению, задаваемому хромосомой Hi(t), то есть xi (t)=Hi(t)={ gil|l=1, 2, …, n}. Число осей в пространстве решений равно числу n генов в хромосомеНi(t). Точками отсчета на каждой оси l являются дискретные целочисленные значения генов.
Принципы кодирования хромосом и механизмы перемещения частиц
в аффинном пространстве
Поскольку в качестве структуры данных, несущих информацию об упаковке, используется последовательность номеров прямоугольников, представляющая порядок их укладки, в работе предлагается подход к построению структур и принципов кодирования гомологичных хромосом (имеющих одинаковый набор отличающихся друг от друга генов).
Пространство поиска включает число осей, равное числу элементов списка (число генов в хромосоме). Каждая ось (номер оси) соответствует номеру позиции элемента в списке. Точками отсчета на оси являются значения элементов списка. Расположены точки счета на оси в одном заранее выбранном порядке, принятом в качестве базового.
Хромосома, описывающая решение, имеет следующую структуру: Нi(t)={gil(t)|l=1, 2, …, n}. Значение гена gil(t) равно значению соответствующего элемента списка Mi.
Пусть в качестве базового списка используется список B=<1, 7, 21, 4, 8, 18>. |B|=6. Пространство поиска X включает 6 осей: X1–X6, в соответствии с числом элементов списка. Каждая ось соответствует позиции списка. Точками отсчета xij на оси Xi=<xij|j=1, 2, …, 6> являются упорядоченные значения элементов списка В, Xi=<xi1=1,xi2 =7, xi3=21, xi4=4, xi5=8, xi6 =18>=<1, 7, 21, 4, 8, 18>.
Например , список Mi=<21, 8, 7, 1, 8, 4, 18> представляется в виде позиции Нi={x13, x25, x32, x41, x54, x66}.
Подобные списки лежат в основе интерпретаций решений в задачах упаковки, разбиения, размещения, планирования работы многопроцессорных вычислительных систем и в ряде других задач.
В связи с требованием к гомологичности хромосом в генетическом алгоритме допускается использование операторов кроссинговера и мутации, не нарушающих гомологичность хромосом.
В процессе поиска методом роя частиц каждая частица перемещается в новую позицию [14]. Новая позиция в канонической парадигме роя частиц определяется как
xi (t+1)=xi(t)+ vi(t+1), (1)
где vi(t+1) – скорость перемещения частицы из позиции xi(t) в позицию xi(t+1). Начальное состояние определяется как xi(0), vi (0) [1].
Приведенная формула представлена в векторной форме. Для отдельного измерения j пространства поиска формула примет вид
xij (t+1)=xij(t)+ vij(t+1), (2)
где xij(t) – позиция частицыpi в измерении j; vij(t+1) – скорость частицы pi в измерении j.
Введем обозначения:
xi (t) – текущая позиция частицы, fi(t) – значение целевой функции частицы pi в позиции xi(t) ;
x* i (t) – лучшая позиция частицы pi, которую она посещала с начала первой итерации, а f*i(t) – значение целевой функции частицы pi в этой позиции (лучшее значение с момента старта жизненного цикла частицы pi);
x* (t) – позиция частицы роя с лучшим значением целевой функции f*(t) среди частиц роя в момент времени t.
Тогда скорость частицы pi на шаге (t+1) в измерении j вычисляется как
vij (t+1) = w∙vij(t)+k1∙rnd(0,1)∙(x*ij(t)–xij(t))+k2∙rnd(0,1)∙(xj(t)–xij(t)), (3)
где rnd(0,1) – случайное число на интервале (0,1); ( w, k1, k2) – некоторые коэффициенты.
Скорость vi(t+1) рассматривается как средство изменения решения.
В отличие от канонического метода роя частиц в рассматриваемом случае скорость vi(t+1) не может быть представлена в виде аналитического выражения с целочисленными дискретными значениями переменных. Если в качестве позиции используется хромосома, то число параметров, определяющих положение частицы в пространстве решений (позицию), должно быть равно числу генов в хромосоме. Значение каждого гена откладывается на соответствующей оси пространства решений. В этом случае возникают некоторые требования к структуре хромосомы и значениям генов. Значения генов должны быть дискретными и не зависеть друг от друга. В качестве аналога скорости vi(t+1) выступает оператор направленной мутации (ОНМ), суть которого в изменении целочисленных значений генов в хромосоме Нi(t). Перемещение частицы pi в новую позицию означает переход от хромосомы Нi(t) к новой – Нi(t+1) c новыми целочисленными значениями генов gil. В работе предлагается подход к построению структур и принципов кодирования гомологичных хромосом (имеющих одинаковый набор генов), обеспечивающих их гомологичность и возможность одновременного использования в генетическом алгоритме и в алгоритме на основе роя частиц, полученными после применения ОНМ.
По аналогии с каноническим методом роя частиц позицию x*i(t) будем называть когнитивным центром притяжения, а позицию x*(t ) – социальным центром притяжения. Когнитивный центр выступает в роли индивидуальной памяти о наиболее оптимальных позициях данной частицы. Благодаря социальному центру частица имеет возможность передвигаться в оптимальные позиции, найденные соседними частицами.
Как уже указывалось выше, позиции задаются хромосомами. Позициям x (t), xi(t), x*i(t) , xсi(t) соответствуют хромосомы Н*(t)={g*l(t)||l=1, 2, …, nl}, Нi(t)={gil(t)|l=1, 2, …, nl}, Н*i(t)={g*il(t)|l=1, 2, …, nl} Нсi(t={gсil(t)|l=1, 2, …, ni}.
В качестве оценки степени близости между двумя позициями xi(t) и xz( t) будем использовать величину Siz расстояния (аффинной связи) между хромосомами Нi(t) и Нz( t).
Целью перемещения хромосомы Нi(t) в направлении хромосомы Нz(t) является сокращение расстояния между ними.
Для учета одновременного тяготения частицы pi к лучшей к позиции x*(t) среди частиц роя в момент времени t и к лучшей позиции x* i(t) частицы pi, которую она посещала с начала первой итерации, формируется виртуальный центр (позиция) притяжения xc i(t) частицы pi. Формирование виртуальной позиции xci(t) осуществляется путем применения процедурывиртуального перемещения из позицииx*i(t) в виртуальную позицию xci(t) по направлению к позиции x*(t). После определения центра притяжения xc i(t) частица pi перемещается в направлении виртуальной позиции xci(t) из позицииxi(t) в позицию xi(t+1). После перемещения частицы pi в новую позицию xi(t+1) виртуальная позиция xc i(t) исключается.
Локальная цель перемещения частицы pi – достижение ею позиции с наилучшим значением целевой функции. Глобальная цель роя частиц – формирование оптимального решения задачи.
Суть процедуры перемещения, реализуемой ОНМ в алгоритме роя частиц, заключается в изменении взаимного расположения элементов в списке (генов в хромосоме). Частица pi перемещается из позиции Нi(t) в направлении позиции в новую позицию Нi(t+1) c новым взаимным расположением элементов в списке.
Введем характеристику, отражающую степень различия между позициямиНi(t) и Hz( t). Для этого произведем сравнение взаимного расположения элементов у всех возможных пар генов в сравниваемых позициях Н i(t) и Hz(t). Пусть Siz(t) – число пар, у которых взаимное расположение элементов в сравниваемых позицияхНi(t) и Hz( t) не совпадает.
Чем больше Siz(t), тем больше различие междуНi(t) и Hz(t), и наоборот, чем меньше Siz( t), тем различие меньше. Тяготение частицы pi в позиции Нi(t) к лучшей позиции Hz(t) выражается в стремлении уменьшения различия между Нi( t) и Hz(t), то есть уменьшения показателя Siz(t). Будем считать, чем меньше различие между Нi(t) и Hz(t), тем ближе позицияНi(t) к лучшей позиции Hz(t).
Модификация позиции Нi(t), то есть переход к позиции Нi(t+1), производится путем выборочных групповых парных перестановок соседних элементов в позиции Нi(t). Модификация позиции Нi(t) выполняется за два такта.
На первом такте формируется множество D1 непересекающихся пар элементов в позиции Нi(t), таких, у которых индекс l – нечетное число:P1={(gil(t), gil + 1(t))|l=1, 3, 5, …}. Подсчитывается число пар Siz(t) в множестве D1, у которых взаимное расположение элементов пары в позиции Нi(t) не совпадает с взаимным расположением этих элементов в позиции Hz( t). Принимается решение о перестановке элементов каждой такой пары в позиции Нi(t), вычисляются показатели Sik(t) и осуществляется модификация Нi(t).
На втором такте формируется множество D2 непересекающихся пар элементов в позиции Н i(t), у которых индекс l – четное число: D2={(gil(t ), gil+1(t))|l=2, 4, 6, …}. Подсчитывается число пар Siz(t) множества D 2, у которых взаимное расположение элементов пары в позиции Нi(t) не совпадает с взаимным расположением этих элементов в позиции Hz(t). Принимается решение о перестановке элементов каждой такой пары в позицииНi(t), вычисляются показателиSik(t+1) и формируется позиция Н i(t+1).
Перестановка выполняется с вероятностью Р=α Siz(t)/n, где n – число пар множества D.
Отметим, что изменение взаимного расположения пары соседних элементов в позиции не приводит к изменению относительного расположения каждого элемента пары с остальными элементами позиции, а также к изменению взаимного расположения остальных элементов друг относительно друга.
Пример работы процедуры перемещения.
Пусть позиции Нi(t) иHz(t) имеют вид:Hi(t)={1, 3, 2, 10, 8}, Hz(t)={1, 10, 2, 3, 8}. Siz(t)=2.
На первом такте шага t формируется множество пар D 1=(1, 3), (2, 10). Взаимное расположение элементов пары (1, 3) в Нi(t ) и Hz(t) совпадают, пары (2, 10) – нет. Отсюда Siz(t1)=1. Переставляются в Hi(t) местами элементы пары (2, 10). Hi(t1)={1, 3, 10, 2, 8}.
На втором такте формируется множество пар D2=(3, 10), (2, 8). Взаимное расположение элементов пары (2, 8) в Нi(t1) иHz(t) совпадают, пары (3, 10) – нет. Отсюда Siz(t2)=1. Переставляются в Hi(t1) местами элементы пары (3,10). Hi(t+1)={1, 10, 3, 2, 8,} . Siz(t+1)=1.
Механизмы улучшения упаковки блоков
Сформируем для прямоугольников Rk={ rki|i=1, 2, …, m} одного блока bk полный неориентированный граф с взвешенными ребрами Gk(Xk, Uk), где Xk – множество вершин, соответствующих множеству прямоугольников Rk, ukijÎUk – ребро, связывающее вершины xki и xkj. Вес ребра φ(ukij) равен сумме высот связываемых им вершин: φ(ukij)=(lki+ lkj). Определяются множества прямоугольников X1k и X2k, расположенных соответственно на верхнем и нижнем уровнях блока bk, X1k È X 2k =Xk.
Пусть l*k1 и l0k1 – соответственно максимальная и минимальная высота прямоугольников, входящих в подмножество Rk1. Соответственно,l*k2 и l0k2 – максимальная и минимальная высота прямоугольников, входящих в подмножество Rk2. Минимально возможная высота Fk блока bk, образованного двумя уровнями Rk1 и Rk2, определится как большее из двух величин (l*k1+l0k1) и (l*k2 +l 0k2):
Fk = max((l*k1+h0k1), (l*k2+l0 k2)). (4)
Зададим ограничения на взаимное расположение прямоугольников по вертикали в одном блоке с помощью двудольного графа ограничений Dk(X1kÈX2k,Ek), где X1k и X2 k – множества вершин, соответствующих множествам прямоугольников, расположенных на нижнем и верхнем уровнях блока соответственно; Ek – множество ориентированных ребер, связывающих вершины множества X1k с вершинами множества X2 k. Наличие ребра ekij означает, что прямоугольник xkj Î Xk2 должен располагаться выше xkiÎXk1, xkjÎXk2.
В результате сближения уровней блока отдельные прямоугольники верхнего уровня будут соприкасаться с прямоугольниками нижнего уровня.
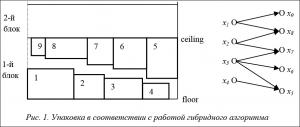
На рисунке 1 показано исходное расположение прямоугольников в блоке, полученное после работы гибридного алгоритма и выполнения процедуры сближения. На этом же рисунке представлен двудольный граф для данного расположения прямоугольников. Минимально возможная высота блока в соответствии с формулой (4) определяется как
Fk =φ(u54)=(l5 + l 4). (5)
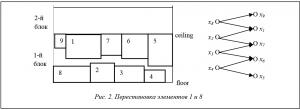
Состояние, при котором два прямоугольника соприкасаются друг с другом по вертикали, будем называть конфликтом. На рисунке 1 в состоянии конфликта находятся прямоугольники 5 и 3. Высота блока определяется размерами этих прямоугольников: φ(u 53)=(l 5 +l 3). Поскольку Fk<φ(u 53), существует потенциальная возможность улучшить решения. Для этого необходимо ликвидировать конфликт между прямоугольниками 5 и 3. Ликвидация конфликта осуществляется путем парных перестановок. Перестановка называется реализуемой, если после ее выполнения суммарная ширина прямоугольников, располагающихся как на верхнем, так и на нижнем уровнях, не превосходит ширины полосы, не появляются новые конфликты и наложения прямоугольников. Затем путем последовательного просмотра реализуемых перестановок отыскивается та, при которой ликвидируется конфликт. Отметим, что в общем случае такой перестановки может и не быть. Для нашего примера: перестановки (3:6), (3:7) нереализуемы, а перестановка (1:8) реализуема. На рисунке 2 показано расположение прямоугольников после обмена расположением прямоугольников 1 и 8.
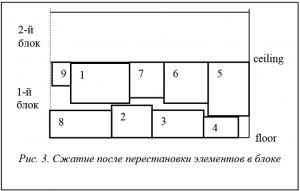
После смены расположения прямоугольников 1 и 8 появляется возможность дополнительного сближения, что приводит к уменьшению высоты блока (рис. 3).
Временная сложность этого алгоритма определяется как O(n 2).
Улучшающий алгоритм решения, полученного алгоритмом упаковки на основе гибридного алгоритма [14], формулируется следующим образом.
1. В качестве исходных данных служит множество блоков B={ bk|k=1, 2, …, nb }, сформированных гибридным алгоритмом и процедурой сужения. Для каждого блока bk задано начальное расположение Ω k уложенных в нем прямоугольников.
2. k=1 (k – номер блока).
3. Выбирается блок bk. Определяется множество прямоугольников X1k и X2k, расположенных соответственно на верхнем и нижнем уровнях блока bk.
4. Строится полный граф Gk(Xk, Uk).
5. Строится двудольный граф ограничений Dk(X1kÈX2k, Ek) для расположения Ω k в блоке bk.
6. Рассчитывается минимально возможная высота Fk блока bk в соответствии с формулой (3).
7. Отыскивается пара прямоугольников α=(rki,rkj), rkiÎX1k1 и rkjÎ Xk2, находящихся в конфликте друг с другом, такая, что Fk <φ(ukij)=(lki+ lkj) Если такой нет, то переход к пункту 9, иначе переход к пункту 8.
8. Путем последовательного просмотра парных реализуемых перестановок прямоугольников в блоке отыскивается та, при которой ликвидируется конфликт пары α=(rki, rkj). Если такая перестановка существует, то с учетом этой перестановки формируется новое расположение Ωk элементов в блоке и переход к пункту 9. Если таких перестановок нет, то переход к пункту 10.
9. Осуществляется сближение верхнего и нижнего уровней блока. Рассчитывается высота блока lк. Если Fk <lк, то переход к пункту 7, иначе переход к пункту 10.
10. Конец работы алгоритма.
Экспериментальные исследования
На основе рассмотренной парадигмы разработана программа SWARM-1.5 DBP для упаковки полуограниченной полосы. Для проведения экспериментальных исследований программы была использована процедура синтеза контрольных примеров с известным оптимумом Fопт по аналогии с известным методом AFEKO – Floorplanning Examples with Known Optimal area [19]. Оценкой качества служит величина Fопт/ F – «степень качества», где F – оценка полученного решения. На первом этапе синтезировались решения с помощью гибридного алгоритма. Затем к каждому такому решению применялся улучшающий алгоритм.
При исследовании сходимости гибридного роевого алгоритма для каждого эксперимента запоминался номер генерации, после которой не наблюдалось улучшение оценки решения. В каждой серии из 50 испытаний определялись минимальный и максимальный номера генерации. Кроме этого, рассчитывалось среднее значение числа генераций, после которого не наблюдалось улучшение оценки. Для каждой серии испытаний определялось лучшее решение, которое фактически являлось оптимальным.
Исследования показали, что число итераций, при которых алгоритм находил лучшее решение, лежит в пределах 110–130. Алгоритм сходится в среднем на 125-й итерации. При этом отклонения числа итераций в большую сторону до 10 %, а в меньшую сторону до 55 %. В результате проведенных исследований установлено, что качество решений у гибридного алгоритма на 4–6 % лучше качества решений генетического и на 4–8 % роевого алгоритмов по отдельности. Эксперименты показали, что увеличение популяции М больше 100 нецелесообразно, так как это не приводит к заметному изменению качества.
Использование улучшающего алгоритма упаковки позволило достигнуть улучшения показателя качества на 2–3 %.
Вероятность получения глобального оптимума составила 0,96. В среднем запуск программы обеспечивает нахождение решения, отличающегося от оптимального менее чем на 2 %. Временная сложность алгоритма при фиксированных значениях M и T лежит в пределах О(n). Общая оценка временной сложности лежит в пределах О(n2)–О(n 3). Задачи, на которых был протестирован разработанный алгоритм, доступны в библиотеке OR-объектов (http://www.ms.ic.ac.uk/info.html). По сравнению с существующими алгоритмами [4–11, 20] достигнуто улучшение результатов на 2–4 %.
Заключение
Исходя из анализа решений, получаемых алгоритмами, построенными на различных метаэвристиках и эвристиках, было установлено, что большинство из них может быть улучшено. На основании этих выводов была разработана новая гибридная поисковая архитектура алгоритма для решения ЗРУ прямоугольных предметов на основе интеграции роевого интеллекта и генетической эволюции. Связующим звеном в таком подходе является единая структура данных, описывающая решение задачи в виде хромосомы. Ключевая проблема, которая была решена в данной работе, связана с разработкой структуры аффинного пространства позиций, позволяющей отображать и осуществлять поиск интерпретаций решений с целочисленными значениями параметров. В отличие от канонического метода роя частиц для уменьшения веса аффинных связей путем перемещения частицы pi в новую позицию аффинного пространства решений разработан оператор направленной мутации, суть которого заключается в изменении связанных целочисленных значений генов в хромосоме. Разработаны новые структуры хромосом для представления решений. Предложенный модифицированный алгоритм декодирования повышает целенаправленность поиска, включает процедуры улучшения решения и обеспечивает более высокую вероятность локализации глобального экстремума задачи. Это позволило повысить качество решения в среднем на 2 –4 %.
Работа выполнена при финансовой поддержке гранта РФФИ № 18-07-00737.
Литература
1. Bischoff E.E. and Wäscher G. Cutting and packing. Europ. J. of Operational Research, 1995, vol. 84, pр. 503–505.
2. Ross P., Marin-Blazquez J.G., Schulenburg, S., and Hart E. Learning a procedure that can solve hard bin-packing problems: a new ga-based approach to hyper-heuristics. Proc. Conf. GECCO, Chicargo, USA, 2003, рр. 1295–1306.
3. Валеева А.Ф. Применение конструктивных эвристик в задачах раскроя-упаковки // Информ. технологии. 2006. № 11. С. 1–24.
4. Тимофеева О.П., Соколова Э.С., Милов К.В. Генетический алгоритм в оптимизации упаковки контейнеров // Тр. НГТУ. Информатика и системы управления. 2013. № 4. С. 167–172.
5. Лебедев О.Б., Зорин В.Ю. Упаковка на основе метода муравьиной колонии // Изв. ЮФУ. 2010. № 12. С. 25–30.
6. Лебедев Б.К., Лебедев В.Б. Планирование на основе роевого интеллекта и генетической эволюции // Изв. ЮФУ. 2009. № 2. С. 25–33.
7. Лебедев Б.К., Лебедев О.Б., Лебедева Е.М. Модернизированный муравьиный алгоритм синтеза идентифицированного дерева гильотинного разреза при планировании СБИС // Изв. ЮФУ. 2017. № 7.
С. 15–28.
8. Мухачева Э.А., Назаров Д.А. Конструирование прямоугольных упаковок: алгоритм перестройки на базе блочных структур // Автоматика и телемеханика. 2008. № 2. С. 97–113.
9. Месягутов М.А., Мухачева Э.А., Белов Г.Н., Шайтхауэр Г. Упаковка одномерных контейнеров с продолженным выбором идентичных предметов: точный метод поиска оптимального решения // Автоматика и телемеханика. 2011. № 1. С. 154–173.
10. Matayoshi M. Two dimensional rectilinear polygon packing using genetic algorithm with a hierarchical chromosome. Proc. IEEE Intern. Conf. SMC, 2011, рp. 989–996.
11. Ахтямов А.А., Картак В.М. Упаковка и оценка плотности упаковки ортогональных многоугольников в полубесконечную полосу // Информационные технологии интеллектуальной поддержки принятия решений : сб. тр. конф. Уфа: Изд-во УГТУ, 2014. С. 117–121.
12. Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой. М.: Изд-во МГТУ им. Н.Э. Баумана, 2014. 448 с.
13. Clerc M. Particle swarm optimization. ISTE Publ., 2006, 244 p.
14. Kennedy J., Eberhart R.C. Particle swarm optimization. Proc. IEEE Intern. Conf. on Neural Networks, 1995, pp. 1942–1948.
15. Blum C., Roli A. Metaheuristics in combinatorial optimization: overview and conceptual comparison. ACM Computing Surveys, 2003, no. 35, pр. 268–308.
16. Лебедев Б.К., Лебедев О.Б. Распределение ресурсов на основе гибридных моделей роевого интеллекта // Науч.-технич. вестн. ИТМО. 2017. Т. 17. № 6. С. 1063–1073.
17. Raidl G.R. A Unified View On Hybrid Metaheuristics. LNCS, Springer, 2006, pр. 1–12.
18 Лебедев Б.К., Лебедев О.Б., Лебедева Е.О. Роевой алгоритм планирования работы многопроцессорных вычислительных систем // Инженерный вестн. Дона. № 3, 2017.
19. Cong J., Romesis M. and Xie M. Optimality, scalability and stability study of partitioning and placement algorithms. Proc. Intern. Sympos. on Physical Design, Monterey, CA, 2003, рp. 88–94.
20 Лебедев Б.К., Лебедев В.Б., Лебедев О.Б. Гибридизация роевого интеллекта и генетической эволюции на примере размещения // Программные продукты, системы и алгоритмы. 2017. № 4. URL: http://swsys-web.ru/mechanisms-of-the-roving-algorithm-for-finding-the-solution-of-the-problem-of-distribution-of-connections.html (дата обращения: 18.05.18).
Комментарии