Идеи теории вейвлетов возникли, когда появилось достаточное количество рядов экспериментальных данных, обработка которых стандартным и хорошо развитым методом преобразований Фурье показала его ограниченность для поиска закономерностей в них. Свою роль сыграло и бурное развитие вычислительной техники, что позволило численно решать такие задачи, которые до этого были просто неподъемными. Одним из первых определенную недостаточную информативность анализа Фурье понял А. Хаар, который в 1910 году опубликовал систему базисных функций, обладающую основными свойствами вейвлетов (сам термин появился значительно позже – через 70 с лишним лет). Система функций Хаара обладала главными свойствами, специфичными для вейвлетов: локальной областью определения (ограниченными носителями), ортогональностью и единичной нормой, нулевым средним и самоподобием (автомодельностью). В настоящее время, однако, многие исследователи, особенно работающие в практических приложениях, понимают под вейвлетами более широкий класс функций. Это и вейвлет-локальные тригонометрические базисы (вейвлеты Малвара), и мультивейвлеты, и так называемые вейвлеты второго поколения, не являющиеся сдвигами и растяжениями одной базисной функции [1].
Вейвлеты непосредственно связаны с многомасштабным анализом и обработкой сигналов различной природы. Предположим, мы хотим изучить какой-то сигнал, например временной ряд. Идея многомасштабного анализа состоит в том, чтобы взглянуть на сигнал при различных масштабах: условно говоря, сначала − под микроскопом, затем − через лупу, потом − на расстоянии нескольких шагов и наконец − совсем издалека. И при каждом масштабе рассмотрения вейвлет-анализ позволяет увидеть те особенности сигнала, которые характерны для данного масштаба, эффективно отфильтровывая влияние других масштабов [1].
Перечислим некоторые области, где использование вейвлетов может оказаться (или уже является) весьма перспективным [2].
Обработка экспериментальных данных. Поскольку вейвлеты появились именно как механизм обработки экспериментальных данных, их применение для решения подобных задач представляется весьма привлекательным до сих пор. Вейвлет-преобразование дает наиболее наглядную и информативную картину результатов эксперимента, позволяет очистить исходные данные от шумов и случайных искажений и даже на глаз подметить некоторые особенности данных и направление их дальнейшей обработки и анализа.
Обработка изображений. Наше зрение устроено так, что мы сосредоточиваем свое внимание на существенных деталях изображения, отсекая ненужное. Используя вейвлет-преобразование, мы можем сгладить или выделить некоторые детали изображения, увеличить или уменьшить его, выделить важные детали и даже повысить его качество.
Сжатие данных. Особенностью ортогонального многомасштабного анализа является то, что для достаточно гладких данных полученные в результате преобразования детали в основном близки по величине к нулю и, следовательно, очень хорошо сжимаются обычными статистическими методами. Огромным достоинством вейвлет-преобразования является то, что оно не вносит дополнительной избыточности в исходные данные и сигнал может быть полностью восстановлен с использованием тех же самых фильтров. Кроме того, отделение в результате преобразования деталей от основного сигнала позволяет очень просто реализовать сжатие с потерями – достаточно просто отбросить детали на тех масштабах, где они несущественны. Стоит подчеркнуть, что изображение, обработанное вейвлетами, можно сжать в 3−10 раз без существенных потерь информации (а с допустимыми потерями – до 300 раз!). В качестве примера отметим, что вейвлет-преобразование положено в основу стандарта сжатия данных MPEG4.
Нейросети и другие механизмы анализа данных. Большие трудности при обучении нейросетей (или настройке других механизмов анализа данных) создает сильная зашумленность данных или наличие большого числа особых случаев (случайные выбросы, пропуски, нелинейные искажения и т.п.). Такие помехи способны скрывать характерные особенности данных или выдавать себя за них и могут сильно ухудшить результаты обучения. Поэтому рекомендуется очистить данные прежде чем анализировать их. По уже приведенным выше соображениям, а также благодаря наличию быстрых и эффективных алгоритмов реализации вейвлеты представляются весьма удобным и перспективным механизмом очистки и предварительной обработки данных для использования их в статистических и бизнес-приложениях, системах искусственного интеллекта и т.п.
Системы передачи данных и цифровой обработки сигналов. Благодаря высокой эффективности алгоритмов и устойчивости к воздействию помех вейвлет-преобразование является мощным инструментом в тех областях, где традиционно использовались другие методы анализа данных, например преобразование Фурье. Возможность применения уже существующих методов обработки результатов преобразования, а также характерные особенности поведения вейвлет-преобразования в частотно-временной области позволяют существенно расширить и дополнить возможности подобных систем.
Распознавание изображений, полученных в результате приема пришедшей от распознаваемого объекта пространственно распределенной электромагнитной энергии, является актуальной задачей современной радиолокации. Один из путей ее решения – создание для обработки принимаемых изображений
алгоритмов, использующих методы цифровой обработки данных. Однако вследствие трудоемкости известных алгоритмов распознавания возникает проблема обеспечения ее решения в реальном масштабе времени с высокой степенью качества. Предлагается новый алгоритм распознавания, полученный с использованием математического аппарата вейвлет-преобразования, который позволяет найти одно из решений данной задачи [3]. Блок-схема данного алгоритма распознавания представлена на рисунке.
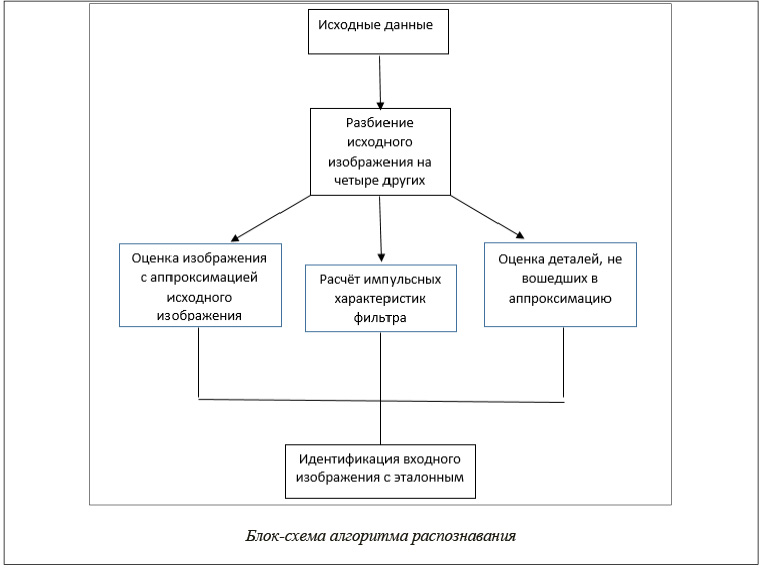
Информация о принятом кадре изображения (ПКИ) в результате его дискретизации на основе методов цифровой обработки содержится в матрице изображения (МИ). Индексы каждого элемента этой матрицы совпадают со значениями неотрицательных целочисленных координат каждого пикселя ПКИ, а значение данного элемента равно уровню яркости этого пикселя [4].
В случае двумерного изображения алгоритм прямого вейвлет-преобразования изображения (ВПИ) можно представить в следующем виде:
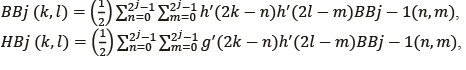
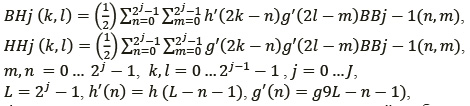
где j − cтепень разрешения; n и m − координаты пикселей изображения BBj-1; k, l − координаты пикселей изображений BBj, HBj, BHj, HHj; h(t), g(t) − импульсные характеристики пространственных фильтров
[5, 6].
Данный алгоритм осуществляет разбиение исходного изображения BBj-1 на четыре, одно из которых, BBj, содержит аппроксимацию исходного изображения BBj-1 с уменьшенным в два раза разрешением, а три других, HBj, BHj, HHj, те детали изображения, которые не вошли в полученную аппроксимацию.
Импульсная характеристика фильтра h(t) описывается вейвлетом Хаара Fh(t), а импульсная характеристика фильтра g(t) − масштабной функцией Хаара Dh(t) [6]:
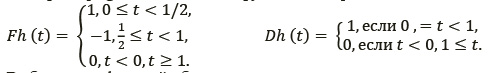
Выбор таких функций обусловлен их негладкостью в смысле конечных разрывов, позволяющих лучше выделять области изображения, имеющие уровень яркости, отличающийся от уровня яркости граничащих с ним областей, то есть позволяет связывать пиксели в бинарные изображения.
При выполнении идентификации входного изображения с эталонным используется алгоритм обратного ВПИ, восстанавливающий изображение BBj-1 из BB'j, HB'j, BH'j и HH'j [5, 6].
Соотношения описывают преобразование исходного изображения BBj в изображение с увеличенной в два раза степенью разрешения BBj-1 путем добавления в BBj деталей, содержащихся в изображениях HBj, BHj, HHj, что соответствует восстановлению исходного изображения:
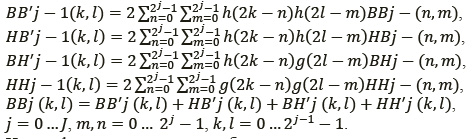
Идентификация исходного изображения на разных уровнях его разрешения при его пошаговом восстановлении в соответствии с алгоритмом определяет процедуру многоуровневой идентификации. Идентификация на каждом уровне разрешения производится путем контурного описания и расфокусировки объектов изображения и получения оценки идентичности, формируемой при свертке полученного контура в исходном изображении с эталонными [3].
Алгоритм идентификации на каждом шаге восстановления имеет вид
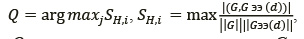
где Q − оценка идентичности контуров; G − контур распознаваемого изображения; Gэi − контур i-го эталонного изображения; d − количество векторов сдвига; Sнi − скалярное произведение векторов [3].
Расфокусировка осуществляется фильтром, имеющим импульсную характеристику вида
,
где r0 − коэффициент расфокусировки; x, y − пространственные координаты [3].
Окончательное решение об идентичности выносится только после выполнения последнего шага восстановления изображения и является конъюнкцией цепочки подтверждающих друг друга решений об идентичности изображений, полученных на разных шагах восстановления, некоторому эталонному. Так как оценка идентичности производится операцией свертки контуров, а это трудоемкая операция, идентификация на крупнодетальном разрешении, при котором контуры изображения содержат меньше векторов, осуществляется значительно быстрее. На мелкодетальном разрешении осуществляются подтверждение выбранного эталона и точная идентификация. Это позволяет решить дилемму между скоростью и качеством идентификации и снизить трудоемкость алгоритма идентификации.
Предложенный алгоритм распознавания изображений, использующий аппарат вейвлет-преобразо-вания, может быть применен при распознавании широкого класса объектов, в том числе для их обнаружения.
Литература
- Нагорнов О.В., Никитаев В.Г. Вейвлет-анализ в примерах: учеб. пособие. М.: Изд-во НИЯУ МИФИ, 2010. С. 4–5.
- Киселев А. Основы теории вейвлет-преобразований. URL: https://basegroup.ru/community/articles/
- intro-wavelets (дата обращения: 22.04.2016).
- Фисенко В.Т. Компьютерная обработка и распознавание изображений: учеб. пособие. СПб: Изд-во СПбГУ ИТМО, 2008. С. 105–107.
- Кревецкий А.В. Обработка изображений в системах ориентации летательных аппаратов. Йошкар- Ола: Изд-во МарГТУ, 1998. С. 113–115.
- Харатишвили Н.Г., Чхеидзе И.М., Ронсен Д., Инджия Ф.И. Пирамидальное кодирование изображений. М.: Радио и связь, 1996. С. 66–70.
- Mulcahy C. Ploting and Scheming with Wavelets. Mathematics Magazine, 1996, vol. 69, no. 5, pp. 323–343.
Комментарии