The task of Natural Language Understanding (NLU) is one of the most important tasks of modern computer science. There are various approaches to its solving, ranging from fairly simple methods used in numerous bots that support a dialogue in a limited problem area to original algorithms, which are implemented, for example, in systems for translating texts from one language to another.
The authors explore an approach based on the LRA semantics (Linguistic Rational Agents) [1]. The main idea of this approach is to represent the text in natural language as formulas of some logic, which would make it possible to effectively solve problems related to knowledge processing and logical inference.
The implementation of text comprehension based on LRA semantics consists in constructing linguistic and rational agents and organizing their subsequent interaction. The idea of this approach is that both aspects of the text (syntactic and semantic) are extremely important for understanding the meaning, and the main problem is to harmonize these aspects. It is assumed that a particular text allows a single syntactic meaning that a linguistic agent can construct. This value can be interpreted in different ways depending on the problem being solved. Such an interpretation that can only be obtained based on extralinguistic knowledge is the meaning of the text. It is also worth noting that from the LRA point of view, a text can have several meanings depending on the rational agents involved in the analysis, but it always has only one meaning received by the linguistic agent [2].
In order to get the meaning of the text, the linguistic agent must first perform a number of standard steps for analyzing a text, which are aimed at its structuring and disambiguation. One of the first stages is morphological analysis; its purpose is to match each source text lexeme with a set of morphosyntactic attributes (grammemes) and a dictionary form (lemma). Both of these tasks are extremely important. Grammemes are essential for deep parsing. The completeness of the set of grammes is a key factor for the subsequent extraction of semantic relationships between objects. Lemmatization allows the linguistic agent to abstract from complex word form matching rules, which simplifies the subsequent analysis stages and allows more accurate determining the meaning of specific words. This effect is especially strong when working with highly inflectional languages, such as Russian. Both of these problems can be solved jointly and separately. This work proposes an improved algorithm for solving the lemmatization problem.
The classical statement of the lemmatization problem is as follows: to find a lemma for a given word form and a set of grammes (initial word form). The problem has a unique solution in this formulation. But there are problems associated with the need to find the appropriate set of grammes that require context analysis. In practice, a number of situations require to find a lemma for a word form when grammes are completely or partially unknown. In this situation, the solution for words that have homonyms is a set of lemmas, one for each homonym.
The complexity of the lemmatization task also is in the fact that a living natural language develops dynamically and continuously, and the linguistic resources currently available do not cover it in full. Therefore, the problem of lemmatization of the so-called non-dictionary words arises.
There are recent studies comparing various software modules for solving the problem of morphological analysis [3, 4, 5]. Implementations differ in a set of functional properties, a set of grammars used, and the work quality. Classical solutions based on dictionaries, decision trees and hidden Markov models (Pymorphy [6], TreeTagger [7], MyStem [8], TnT [9], etc.) are still the most popular due to their relative simplicity, it is enough high precision and speed. Methods based on neural networks show the highest accuracy. However, various problems associated with performance and the learning process prevent their widespread use for solving applied NLU problems.
The lemmatization task in such modules is considered as a separate one, not connected in any way with the main analysis process. Most of the developed algorithms for solving it somehow use a certain dictionary, external or automatically extracted from the text corpus. The simplest dictionary has the form of a table, where each word is associated with its lemma. Then there is no parsing of non-dictionary words. Another popular approach is using prefix trees. This approach uses advantage of the morphological features of inflectional languages, namely the fact that the vast majority of forms are formed by modifying the existing form ending according to certain rules. It is assumed that words that end in the same way are parsed in the same way. This feature allows building a certain prefix tree (or several trees) by expanding words. These trees are typically depth-limited using various heuristics or hyperparameters that aim to find a sufficient suffix length needed for lemmatization.
As it was mentioned above, most of the developed algorithms consider the lemmatization problem separately from the problem of morphological analysis. However, according to the authors, an effective solution of the lemmatization problem in both given formulations can significantly simplify the problem of morphological analysis. This paper proposes a universal lemmatization algorithm UniLemm, which allows solving the lemmatization problem in both formulations for inflectional languages, does not involve optimizing hyperparameters for the particular language needs, and also makes it possible to solve the inverse problem, i.e. obtaining a form with the required grammemes using a lemma. It is also possible to use the algorithm in solving other problems that arise during morphological analysis.
UniLemm algorithm. Building a classification tree
Let us reduce the formulated lemmatization problem to the classification problem. Each word form can be assigned a certain class - a declension paradigm. The paradigm-based approach considers various word forms as special cases of general word-formation rules. At the same time, a specific word-formation rule shows how to obtain a given word form with the desired grammemes from a lemma by adding a certain suffix to the lemma stem. Lemmas with the same sets of rules form a paradigm. The approach has been successfully applied in various morphological analyzers [6, 8].
In the framework of this work, we assume the paradigm P to be the set of declination rules. P = {R1, R 2,…, Rn}. Each Ri rule specifies the following transformation:
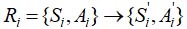
where Si is a suffix of the original word form replaced by suffix. After the replacement, the word form is transformed into a lemma. Ai are grammemes of the original word form replaced by grammemes. As a result, the resulting set of grammemes represents the lemma grammemes.
The task of lemmatization in this approach is reduced to the classification task - finding the desired paradigm and the number of the rule within the paradigm, with the subsequent application of this rule to the original word. Moreover, the rule formulation makes it possible to apply it in the reverse order, to obtain the word form from the lemma. We can get any word form knowing the paradigm and the rule.
One of the approaches used to solve the classification problem is based on the building a classification tree. The classification tree can be based on the training sample. The training sample can be viewed as a set of records with fields containing input parameter data. Each record in the training sample has an indicated class of a target parameter.
Let us take a given set of input parameters. The task of the classifier is to determine the object class from this set with the presented values. A typical example is pattern recognition. The classifier is presented with pictures of objects, in response it gives out the object class: this is a “rabbit”, this is a “hare”, this is a “wolf”. In our case, the classifier is presented with a word form and a set of its grammemes. In response, it issues a word form class - a paradigm and the corresponding rule.
An object class is a target parameter. It has a discrete type with a finite number of values. The parameter values are class names, also called class labels.
Typically, the algorithm for building a decision tree belongs to the class of greedy algorithms. It recursively builds a binary decision tree from top to bottom starting from the root. It selects the most informative parameter for each node of the tree and choses its value in the node so as to split the initial sample (database records) into two samples; the classes are separated from each other in the best possible way in each of them. Ideally, one of the selections should contain records that belong to only one class.
There are different ways to select an appropriate parameter and its value in a tree node. For example, we can use an entropy criterion. We reduce the uncertainty in choosing the appropriate class by minimizing the entropy.
We use the well-known Shannon formula to calculate the entropy criterion:
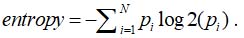
The formula uses pi that are the probabilities of class occurrence calculated as the frequency of occurring classes in the sample.
The task of classifying word forms has its own characteristics due to the choice of a grammeme format and how a training sample and a classification tree are built. Let us consider the solution of these problems in more detail.
Gramme format
A grammeme is a grammatical meaning, one of the grammatical category elements. For example, the Russian language is characterized by such grammatical categories as gender, number, case, etc. These categories can have specific meanings: singular, masculine, nominative case. A set of grammemes for a particular word form is represented as a binary vector; its elements take the value 1 if the word form has the corresponding grammeme, and
0 otherwise. Such representation makes it possible to carry out set-theoretic operations on grammemes effectively. In general, there is no restriction on a single meaning within a grammatical category. However, the order of the grammemes in the vector is important. The algorithm involves working with a fixed set of categories and grammemes, which are known at the stage of building a training set.
There is no generally accepted standard that states many categories and grammars in the Russian language. There are several grammeme annotation systems, ranging from the Russian National Corpus [10], which takes into account the most rare grammatical features, to the Universal Dependencies (UD) notation [11] that, on the contrary, is aimed at abstracting from the language details where possible.
This paper considers the OpenCorpora format [12] as the set of grammemes since it is one of the most grammeme-rich formats. Since not all grammemes are of value as automatic text processing tasks, we have selected 60 grammemes that are the most significant from the point of view of morphological and syntactic analysis tasks. The constructed set of grammemes is a subset of the set of grammemes used in the Russian National Corpus and a superset for UD grammemes, which made it possible to use any of the corpora in developing and testing the model.
A training sample format
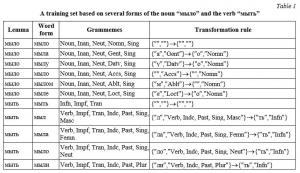
We can consider the training sample represented by the language corpus as a set of pairs containing a word form and a declension rule. The declension rule is represented as a pair including the number of the paradigm and the number of the rule within the paradigm. Let us consider a training set containing some forms of the noun “мыло” and the verb “мыть” as an example.
This training set demonstrates several examples of homonymy. For example, the forms of the noun “мыло” in the nominative and genitive case coincide with the form of the verb “wash” in the past tense and neuter gender. In addition, we can assess the impact of using declination paradigms. So, most verbs of the first conjugation (ending in “-еть”, “-ать”, “-оть”, “-ыть”, “уть” in the initial form, not including exceptions) will change similarly to the verb “мыть” representing one paradigm.
An algorithm for building a classification tree
This paper considers the algorithm that is a modification of the LemmaGen algorithm [13]. The original algorithm is based on building a data structure called the Ripple Down Rule (RDR). RDR rules were originally designed to compactly represent and organize contextual knowledge by representing some form of a decision tree. In [14], this data structure was used to solve the lemmatization problem.
Let us consider how the RDR rules that define the classification tree are built in the presented algorithm.
The tree nodes contain predicates defined over word suffixes and grammemes, and the tree leaves contain lemmatization rules.
There are three stages in the algorithm (Fig. 1). The first stage sorts the input set. As a result, training examples are arranged in lexicographic order according to the inverted word form. Then, based on the sorted set of examples, an RDR (decision tree) is built using a recursive algorithm. The final step of the algorithm is to compress the resulting tree by searching and reusing indistinguishable tree vertices:
The purpose of the LearnRecursive function is to build RDR for a sorted set of training examples.
There are several formal definitions of RDR. In this paper, RDR refers to rules with their syntax represented as a BNF definition:
RDR ∷= IF <condition> THEN <rule> [EXCEPT <RDR_list>]
Thus, RDR is an IF-THEN-EXCEPT rule, where condition is a predicate and rule is a classification rule. The RDR structure can also contain a non-empty list of exception rules that refine the original rule. Thus, RDRs have much in common with decision trees: the rules and their exceptions are ordered, the first rule whose condition is met and none of the conditions of the exception rules is met causes the corresponding rule classification rule (in this case, lemmatization) to work. In general, RDR represents a decision tree that is not binary, but can be reduced to binary by converting the set of exception predicates into a series of one-vs-all predicates.
The proposed algorithm is a recursive RDR construction procedure that splits the current training set into subsets according to some predicate. A predicate can be defined either over a suffix of a word form or over grammemes. Being rule, both RDR variants contain the transformation rule most frequently encountered in the current training set. After forming the predicate and the rule, the algorithm recursively continues its work on the obtained subsets as long as it is possible to construct the corresponding predicate.
The algorithm starts by building a subtree of suffixes. The main idea is that each rule (and therefore subtree) combines the words of the original training set that end in some common suffix. The search for a common suffix takes into account the sorting of the original set. The training set is effectively divided into subsets by the symbol preceding the common suffix. The separation procedure is repeated until only the same words remain in the subset (in the case of homonymy). Then the algorithm proceeds to building a subtree of grammemes. Otherwise, the procedure is activated recursively on the resulting subset.
The algorithm for building a grammeme tree is similar to the classical algorithm for building classification trees. First, we find the grammeme with the lowest entropy value. If several grammemes correspond to a division with the same entropy, then we choose the first grammeme in order. The order of the grammemes in the vector is important: grammemes must be arranged according to some linguistic intuition as to which ones play the biggest role in resolving homonymy. For example, for the Russian language, it is more logical to first determine the part of speech and then ask more specific questions about number, case, gender. This ordering is not necessary, but allows building trees with fewer nodes and a more human-like decision process. In practice, the situation when there are two equivalent features according to the entropy criterion is quite rare (less than 5% of all words for the Russian language). The constructed predicate allows us to divide the training set into subsets and to apply the algorithm to each of them recursively. The stopping rules allow completing the tree building in the tree leaves.
Summarizing the above, we note that the UniLemm algorithm builds a combined classification tree containing suffix subtrees and grammeme subtrees. Suffix trees are for primary classification, while grammeme trees allow resolution of homonymy if any.
At the last stage, the built combined tree is compressed to eliminate possible redundancy.
The resulting tree can be represented as a DFA (Deterministic Final Automaton) under the following
conditions:
· each node in the suffix tree is considered a separate DFA state;
· each grammeme tree as a whole is considered a separate DFA state;
· transformation rules are considered separate DFA end states.
The constructed DFA automaton can be transformed into a similar DAFSA automaton (Deterministic Acyclic Finite State Automaton), which has a minimum number of states. Such automaton can be considered as the end result of the learning algorithm.
Experimental results
We used the OpenCorpora dictionary to build the classification tree and the corresponding automaton.
As usual, a part of the vocabulary was used for learning, the other part for control. We have obtained results for three training options for 50, 80 and 90 percent of the vocabulary.
There is another interesting case when a control sample is not a dictionary but a set of marked up texts, where the word lemmas are known as in a dictionary. For such experiments, we selected two publicly available text corpora:
OpenCorpora subcorpus with removed homonymy. Ii includes texts of various subjects and styles;
UD subcorpus that includes Wikipedia articles. The grammeme format was converted to the OpenCorpora format.
The experimental results are shown in Table 2.
Obviously, the algorithm shows sufficient accuracy for practical use on all control samples.
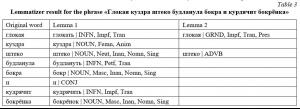
As an example, let us consider the result of the lemmatizer work on non-dictionary words using Academician Shcherba’s famous phrase: “Глокая куздра штеко будланула бокра и курдячит бокрёнка”. In the case when there are no specified grammemes for these words, the lemmatizer was able to unambiguously determine lemmas for all words, except for the words “глокая” and “штеко”. The lemmatizer has created two equivalent variants for these words; they are shown in the Lemma 1 and Lemma 2 columns of Table 3.
When grammemes are partially specified for word forms (it is enough to specify the part of speech), ambiguities are eliminated, the lemmatizer works correctly on all non-dictionary words in this example.
A qualitative analysis of lemmatization errors has shown that most errors are due to proper names and abbreviations, as well as inaccuracies in the markup itself (for example, violation of own rules for assigning infinitives as lemmas for participles and gerunds). In addition, there were found errors in reducing adverbs to adjectives and restoring abbreviations. These and other corpora features were not taken into account when building the original training set.
The accuracy of the UniLemm algorithm is comparable to other lemmatization algorithms [3, 4, 5]. The average parsing speed was 250-300 thousand words per second in a single-threaded mode. Comparative studies show an average speed of tens of thousands of words per second for TreeTagger, TnT, etc. [5, 15]. However, a direct comparison with other morphological analyzers is not entirely correct due to using different packages and hardware.
Conclusion
The UniLemm algorithm was developed as a part of this work. The algorithm accuracy and speed is at least at the level of other widely used tools that solve the lemmatization problem. The trained model can be used not only for lemmatization, but also for inflecting words, as well as generating hypotheses for morphological parsing.
Future areas of research include:
· improving the accuracy of the model for the Russian language taking into account the peculiarities of the training dictionary and the target format of morphological markup,
· learning similar models for other inflectional languages,
· developing an algorithm for morphological analysis based on the obtained model.
We plan using the presented model in the implementation of the lexical component of the text analysis system based on LRA semantics [1] as a basis for morphological analysis and synthesis.
References
1. Dikovsky A. Linguistic↔Rational Agents' Semantics. J. of Logic Language and Information, 2017, vol. 4, no. 26, pp. 1–97.
2. Smirnov I., Billig V. The role of the lexical agent in the LRA semantics. Informatics: Problems, Methods and Technologies. Proc. XX Intern. Conf., 2020, pp. 1683–1689.
3. Trofimov I. Automatic morphological analysis for Russian: Application-oriented survey. Software Engineering, 2019, vol. 10, no. 9-10, pp. 391–399. DOI: 10.17587/prin.10.391-399.
4. Sorokin A., Shavrina T., Lyashevskaya O., Bocharov V., Alexeeva S., Droganova K., Fenogenova A., Granovsky D. MorphoRuEval–2017: An evaluation track for the automatic morphological analysis methods
for Russian. Computational Linguistics and Intellectual Technologies:Proc. Int. Conf. “Dialogue”, 2017, vol. 16, pp. 314 –327.
5. Dereza O., Kayutenko D., Fenogenova A. Automatic morphological analysis for Russian: A comparative study. Computational Linguistics and Intellectual Technologies: Proc. Intern. Conf. “Dialogue”, 2016, available at: http://www.dialog-21.ru/media/3473/dereza.pdf (accessed May, 14, 2022):
6. Korobov M. Morphological analyzer and generator for Russian and Ukrainian languages. Analysis of Images, Social Networks and Texts: Proc. 4th Int. Conf., 2015, pp. 320–332. DOI:10.1007/978-3-319-26123-2_31.
7. Schmid H. Probabilistic part-of-speech tagging using decision trees. New Methods in Language Processing: Proc. Int. Conf., 1994, vol. 12, pp. 44–49.
8. Segalovich I. A fast morphological algorithm with unknown word guessing induced by a dictionary
for a web search engine. Machine Learning; Models, Technologies and Applications: Proc. Int. Conf., 2003,
pp. 273–280.
9. Brants T. TnT – a statistical part-of-speech tagger. ANLC '00: Proc. 6th Conf., 2000, pp. 224–231.
10. Lyashevskaya O.N., Plungyan V.A., Sichinava D.V. On the morphological standard of the Russian national corpus. Russian National Corpus: 2003–2005. Results and prospects, Moscow, 2005, 344 p.
11. Universal Dependencies. 2015, available at: http://www.universaldependencies.org ( accessed May 14, 2022).
12. Bocharov V., Bichineva S., Granovsky D., Ostapuk N. Quality assurance tools in the OpenCorpora. Computational Linguistics and Intelligent Technology: Proc. Intern. Conf. “Dialog”, 2011, pp. 10–17.
13. Jursic M., Mozetic I., Erjavec T., Lavrac N. LemmaGen: Multilingual lemmatisation with induced ripple-down rules. J.UCS, 2010, vol. 16, no. 9, pp. 1190–1214.
14. Plisson J., Lavrac N., Mladenic D., Erjavec T. Ripple down rule learning for automated word lemmatization. AI Communications, 2008, vol. 21, no. 1, pp. 15–26.
15. Horsmann T., Erbs N., Zesch T. Fast or accurate? – A comparative evaluation of PoS tagging models. Proc. Int. Conf. GSCL, 2015, pp. 22–30.
УДК 519.68
DOI: 10.15827/2311-6749.22.2.1
Построение многофункционального лексического компонента
для системы анализа текстов на естественном языке
И.С. Смирнов 1 , аспирант, dru0121@gmail.com
В.А. Биллиг 1 , к.т.н., с.н.с., доцент, профессор, vladimir-billig@yandex.ru
1 Тверской государственный технический университет, кафедра программного обеспечения,
г. Тверь, 170026, Россия
В работе предлагается новый улучшенный алгоритм UniLemm (универсальный лемматизатор), который позволяет решать как прямую задачу – построение леммы слова, так и обратную– построение по лемме словоформ с фиксированными граммемами.
Лемматизатор является важным компонентом продвинутых систем искусственного интеллекта, занимающихся анализом текстов на естественном языке.
Задача лемматизации заключается в приписывании каждому слову входного текста его начальной формы (леммы).
В работе задача лемматизации сводится к задаче классификации. Каждой словоформе с заданными граммемами (грамматическими категориями) приписывается некоторый класс – парадигма склонения, где под парадигмой P понимается множество правил склонения.
При построении классификатора для задачи лемматизации учитывается существование несловарных слов, а также ситуация, когда граммемы для словоформы не заданы.
Для построения дерева классификации используется обучающая выборка, роль которой играет словарь русского языка OpenCorpora. При построении узлов дерева классификации учитываются два важных ортогональных аспекта – суффиксы словоформ и множество граммем. Применяемое в работе множество граммем является подмножеством набора граммем, используемого в национальном корпусе русского языка, и надмножеством для граммем, используемых в нотации Universal Dependencies (UD).
При построении дерева классификации используется оригинальная структура данных на основе RDR-правил, позволяющих формулировать не только правило склонения для словоформы, но и возможные исключения.
Алгоритм UniLemm строит комбинированное дерево классификации, содержащее поддеревья суффиксов и поддеревья граммем. Суффиксные деревья предназначены для первичной классификации, а деревья граммем позволяют разрешать омонимию.
На заключительном этапе алгоритма итоговое дерево классификации представляется в виде детерминированного автомата DFA (Deterministic Final Automaton).
Проверка корректности и качества алгоритма проводилась как на контрольной выборке OpenCorpora, так и на двух подкорпусах, содержащих оригинальные тексты различной тематики и стилистики. Алгоритм показал хорошие результаты b по точности решения задачи лемматизации (выше 90%), и по скорости обработки текстов (250-300 тысяч слов в секунду в однопоточном режиме).
Ключевые слова: обработка естественного языка, морфология, лексикон, дерево решений, парадигма склонения, лемматизация.
Литература
1. Dikovsky A. Linguistic↔rational agents' semantics. J. of Logic Language and Information, 2017, vol. 4, no. 26, pp. 1–97 .
2. Смирнов И.С., Биллиг В.А. Роль лексического агента в семантике LRA // Информатика: проблемы, методы и технологии: матер. XX Междунар. науч. конф. 2020. С. 1683-1689. DOI: 10.17587/prin.10.391–399.
3. Трофимов И.В. Морфологический анализ русского языка: обзор прикладного характера // Программная инженерия. 2019. Т. 10. № 9–10. С. 391–399.
4. Sorokin A., Shavrina T., Lyashevskaya O., Bocharov V., Alexeeva S., Droganova K., Fenogenova A., Granovsky D. MorphoRuEval-2017: An evaluation track for the automatic morphological analysis methods for Russian. Computational Linguistics and Intellectual Technologies: Proc. Int. Conf. “Dialogue”, 2017, vol. 16, pp. 314–327.
5. Dereza O., Kayutenko D., Fenogenova A. Automatic morphological analysis for Russian: A comparative study. Computational Linguistics and Intellectual Technologies: Proc. Int. Conf. “Dialogue”. 2016. URL: http://www.dialog-21.ru/media/3473/dereza.pdf (дата обращения: 14.06.2022).
6. Korobov M. Morphological analyzer and generator for Russian and Ukrainian languages. Analysis of Images, Social Networks and Texts: Proc. 4th Int. Conf., 2015, pp. 320–332. DOI:10.1007/978-3-319-26123-2_31.
7. Schmid H. Probabilistic part-of-speech tagging using decision trees. New Methods in Language Processing: Proc. Int. Conf., 1994, vol. 12, pp. 44 –49.
8. Segalovich I. A fast morphological algorithm with unknown word guessing induced by a dictionary
for a web search engine. Machine Learning; Models, Technologies and Applications: Proc. Int. Conf., 2003, pp. 273–280.
9. Brants T. TnT – a statistical part-of-speech tagger. ANLC '00: Proc. 6th Conf., 2000., pp. 224–231. DOI:10.3115/974147.974178.
10. Ляшевская О.Н., Плунгян В.А., Сичинава Д.В. О морфологическом стандарте Национального корпуса русского языка. Национальный корпус русского языка: 2003–2005. Результаты и перспективы. М., 2005. 344 с.
11. Universal Dependencies. 2015, URL: http://www.universaldependencies.org (дата обращения: 14.05.2022).
12. Bocharov V., Bichineva S., Granovsky D., Ostapuk N. Quality assurance tools in the OpenCorpora. Computational Linguistics and Intelligent Technology: Proc. Int. Conf. «Dialog», 2011, pp. 10–17.
13. Jursic M., Mozetic I., Erjavec T., Lavrac N. LemmaGen: Multilingual lemmatisation with induced ripple-down rules. J.UCS, 2010, vol. 16, no. 9, pp. 1190–1214.
14. Plisson J., Lavrac N., Mladenic D., Erjavec T. Ripple down rule learning for automated word lemmatization. AI Communications, 2008, vol. 21, no. 1, pp. 15–26.
15. Horsmann T., Erbs N., Zesch T. Fast or accurate? – A comparative evaluation of PoS tagging models. Proc. Int. Conf. GSCL, 2015, pp. 22 –30.


Комментарии