Теория идентификации занимается решением задач построения математических моделей динамических систем по данным наблюдений за их поведением. От качества построенной модели зависит качество управления или результатов исследования с помощью построенной модели.

Идентификация динамических объектов является одной из задач, для решения которых наряду с множеством различных методов [1, 2], например статистического анализа [3], могут быть применены нейронные сети [4]. Идентификация объекта может быть затруднена, если неизвестны точная структура модели объекта или точное число параметров объекта, некоторые из параметров объекта изменяются по неизвестным законам. В таких случаях для идентификации динамических объектов могут быть применены нейронные сети. Существует множество типов нейронных сетей, применяющихся при идентификации динамических объектов. Несмотря на большое количество нейросетевых методов идентификации динамических объектов большинство из этих алгоритмов имеют некоторые ограничения или не дают необходимой точности.

Среди всевозможных архитектур нейронных сетей, которые могут быть применены для идентификации динамических объектов, выделяется класс нейронных сетей, основанных на самоорганизующихся картах Кохонена. Нейронным сетям именно такого типа будет уделено особое внимание в данной статье ввиду их все более широкого распространения и успешного применения для решения различных задач распознавания [5], идентификации [6] и др. Также будет рассмотрен ряд биоморфных нейронных сетей, архитектура которых создана в результате исследования строения коры головного мозга млекопитающих.

Нейросетевые структуры на основе самоорганизующихся карт Кохонена
для идентификации динамических объектов

Постановка задачи

Идентификацию динамического объекта, получающего на вход в момент времени t вектор входных параметров u(t) и имеющего на выходе вектор y(t), можно рассматривать как нахождение типа модели этого объекта с выходом 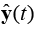 и параметров данной модели, удовлетворяющих условию минимизации ошибки  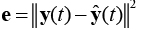этой модели (рис. 1).

Пусть заданы последовательность векторов входных признаков u(t),  , и последовательность векторов выходов y(t), , где T – число дискретных отсчетов. Будем рассматривать решения задачи идентификации как определение вида функции f:

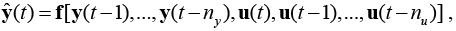
где 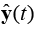 – вектор выходов модели, n_y<<T, n_u<<T. Рассматриваемая схема идентификации называется последовательно-параллельной, в каждый момент времени на вход модели подаются известные измеренные значения входного и выходного сигналов объекта.

Будем также рассматривать решение задачи в виде

,

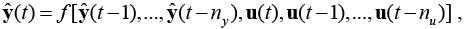где 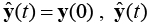, – вектор выходов модели, n_y<<T, n_u<<T. Такую схему идентификации называют параллельной, в каждый момент времени на вход модели подаются измеренные значения входного сигнала объекта и выходы модели в предыдущие моменты времени.

Такая постановка задачи является типичной задачей идентификации динамического объекта с помощью NARX-моделей.

Векторная квантированная темпоральная ассоциативная память
(VQTAM – Vector-Quantized Temporal Associative Memory)

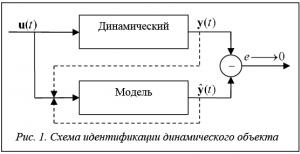
VQTAM – это модификация самоорганизующихся карт Кохонена, которая может быть применена для идентификации динамических систем [7, 8]. Структура данной сети аналогична структуре самоорганизующихся карт Кохонена, ключевое отличие заключается в организации весовых коэффициентов нейронов сети. Вектор входных признаков x(t) данной сети разделен на две части: xⁱⁿ(t ), x^out(t). Первая часть входных признаков xⁱⁿ(t) содержит информацию о входах динамического объекта и его предыдущих выходах. Вторая часть вектора входных признаков x ^out(t) содержит информацию о предполагаемом выходе данного динамического объекта, соответствующем входам xⁱⁿ(t). Вектор весов разделен аналогичным способом [8]. Таким образом 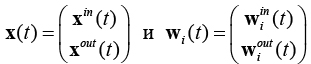, и , где w _i(t) – вектор весов i-го нейрона; w _i ⁱⁿ (t) – часть вектора весов, соответствующая части входного вектораxⁱⁿ(t); w _i^out(t) – часть вектора весов, соответствующая части входного вектора x ^out(t).

Первая часть вектора входных признаков содержит информацию о входах процесса и его предыдущих выходах:

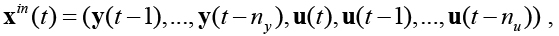
где n_y<<T, n_u <<T.

Вторая часть вектора входных признаков x ^out(t) = y(t) содержит информацию о предполагаемом выходе данного процесса, соответствующем входам xⁱⁿ(t ).

Каждый пример выборки состоит из пары векторов (y( t), u(t)), и выборка должна содержать не менее max(n_u, n_y) примеров. Вектор y(t) представляет собой вектор входов объекта в момент времени t, а u(t) – вектор выходов этого объекта в тот же момент времени.

После подачи на вход сети очередного входного вектора x(t), составленного из нескольких примеров обучающей выборки, нейрон-победитель определяется только по вектору x ⁱⁿ(t):

,

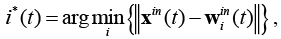где i^*(t) – номер нейрона-победителя на шаге t.

Для изменения весов может быть применено модифицированное правило изменения весов для обычной SOM:

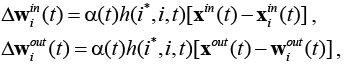
где 0 < a(t) < 1 – скорость обучения сети; h – функция соседства нейрона i и i^*. В качестве функции соседства h(i^*, i, t ) может быть выбрана, например, гауссова функция:

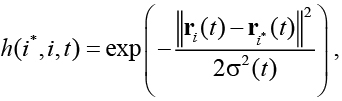
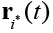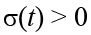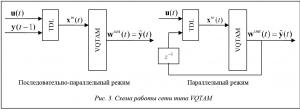
где r _i(t) и  – положения на карте нейронов i и i ^* соответственно;  – определяет радиус функции соседства на шаге t (как правило, выбирается начальное значение данного параметра, убывающее экспоненциально или линейно в зависимости от t ). После выбора нейрона-победителя i ^* выход сети устанавливается равным 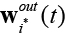 (схема обучения сети отображена на рисунке 2).

В режиме работы на вход VQTAM подается только векторx ⁱⁿ(t), для которого определяется нейрон-победитель, и выход сети устанавливается равным 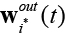 (схема работы сети отображена на рисунке 3). Вектор  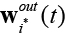может быть интерпретирован как предсказанный выход  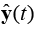объекта в момент времени t.

Также стоит отметить, что данный алгоритм применим к объектам, выход которых может быть описан с помощью как непрерывных, так и разрывных функций.

Рекуррентная самоорганизующаяся карта ( RSOM – Recurrent Self - Organizing Map )

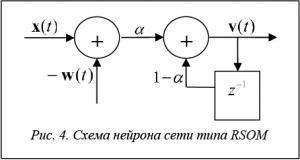
В RSOM, в отличие от обыкновенной карты Кохонена с обратными связями, для каждого нейрона определен вектор выходов, затухающий во времени, по которому определяется нейрон-победитель и по которому происходит изменение весов [9, 10].

Представим вектор входов сети следующим образом:

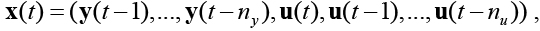
где n_y << T, n_u << T.

Выход каждого нейрона определяется следующим выражением:

,

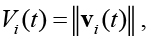где 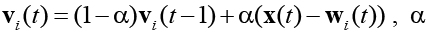– константа, коэффициент затухания выхода 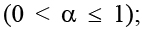V_i (t) – выход i-го нейрона на такте t;w_i(t) – вектор весов i-го нейрона, 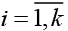, k – количество нейронов сети.

После подачи на вход сети очередного примера нейрон-победитель определяется как нейрон с минимальным выходом [10]:

.

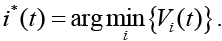Для изменения весов используется измененное правило для обучения карты Кохонена:

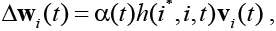
где 0 < a(t) < 1 – скорость обучения сети; h – функция соседства нейрона i и i^*. Схема нейрона такой сети изображена на рисунке 4.

После завершения обучения сеть запускается на обучающей выборке и кластеризует ее, образуя кластеры, которые могут быть аппроксимированы локальными моделями, например, линейными функциями. Для каждого кластера строится локальная модель. Таким образом, после запуска сети на тестовой выборке для каждой точки выборки определяется наиболее подходящая локальная модель, по которой может быть предсказан следующий выход объекта.

Этот процесс можно ускорить, используя алгоритмы построения локальных линейных моделей во время обучения нейронной сети. Такой метод построения моделей применим, если размерность вектора выходов объекта равна одному, поэтому рассматриваемые далее значения y(t) и 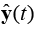 скалярные, также стоит отметить, что такой метод может быть успешно применен только к объектам, выход которых может быть описан непрерывной функцией. Каждому нейрону сети RSOM ставится в соответствие матрица A_i(t), содержащая коэффициенты соответствующей линейной модели:

Выходное значение сети определяется в соответствии со следующим выражением:

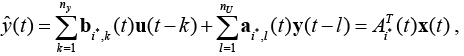
где 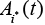– матрица коэффициентов, ассоциированная с нейроном-победителем i^*(t). Матрица  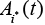используется для линейной аппроксимации выхода модели.

При построении локальных линейных моделей одновременно с обучением нейронной сети необходимо дополнительное правило для изменения коэффициентов линейных моделей:

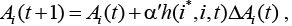
где 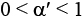– скорость обучения модели, а 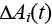– правило коррекции ошибки Уидроу–Хоффа:

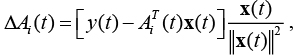
где y(t) – желаемый выход модели при подаче на вход вектора x(t).

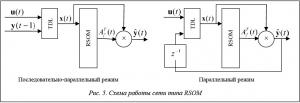
Таким образом, на каждом шаге обучения сети происходит изменение коэффициентов модели вместе с весовыми коэффициентами нейронов. В режиме работы сети после подачи на вход входного вектора сеть определяет нейрон-победитель i*(t). Затем выбирается 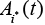 соответствующая матрица коэффициентов линейной модели. С помощью выбранной матрицы выход модели определяется по формуле 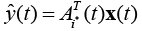. Схемы работы сети типа RSOM отображены на рисунке 5.

Модульные самоорганизующиеся карты

Модульные самоорганизующиеся карты представлены в ряде работ Тетсуо Фурукавы [11, 12]. Модульная SOM имеет структуру массива, состоящего из функциональных модулей, которые представляют собой обучаемые нейронные сети, например, многослойные персептроны (MLP), а не векторы, как в обычных самоорганизующихся картах. В случае MLP-модулей модульная самоорганизующаяся карта выделяет группы особенностей или функций в зависимостях входных и выходных значений, одновременно строя карту их похожести. Таким образом, модульная самоорганизующаяся карта с MLP-модулями представляет собой самоорганизующуюся карту в функциональном, а не в векторном пространстве [12].

Подобные нейросетевые структуры можно считать биоморфными, так как их возникновение во многом обусловлено исследованиями структуры коры головного мозга млекопитающих [13] и подтверждены рядом дальнейших исследований [14]. В основе идеи строения коры головного мозга лежит модель ячеистой структуры, где каждая ячейка является совокупностью нейронов, нейронной колонкой. Колонки нейронов объединены в более сложную структуру. В связи с этим было предложено моделировать колонки нейронов отдельными нейронными сетями [14]. Именно эта идея и легла в основу модульных нейронных сетей.

По сути модульная самоорганизующаяся карта представляет собой обыкновенную карту Кохонена, где нейроны заменены более сложными и самостоятельными структурами, такими как другие нейронные сети. Такая замена требует небольшой модификации алгоритма обучения.

В предложенном Фурукавой алгоритме [12] на начальном этапе обучения сеть запускается на i-й выборке входных данных, соответствующей I различным образам (применительно к задаче, решаемой в данной работе, различным состояниям динамического объекта), карту сходства которых может построить сеть, и рассчитывается ошибка каждого модуля сети:

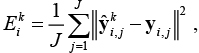
где k – номер модуля, для которого рассчитана ошибка; J – число точек в выборке; 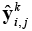 – выход k-го модуля; y _i,j – ожидаемый выход сети на предложенном наборе входных данных. Модуль-победитель определяется как модуль, минимизирующий ошибку :

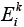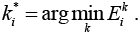
Как только модуль-победитель определен, происходит адаптация весов сети – сначала адаптируются веса модуля-победителя по одному из возможных алгоритмов обучения сетей такого типа, после этого начинается адаптация весов карты. В этом процессе параметры каждого из модулей рассматриваются как веса карты и адаптируются по стандартным алгоритмам самоорганизующихся карт Кохонена.

В статьях Фурукавы подобные нейронные сети используются для построения различных карт подобия, интерполяции, а также для распознавания образов. В данной работе модульные сети были успешно применены для идентификации динамических объектов, при этом разработаны уникальные, ранее не предлагавшиеся модульные структуры, где в качестве модулей использованы сети типа VQTAM и RSOM, описанные выше.

Нейронная модульная сеть, где в качестве модулей применены сети типа VQTAM (то есть сеть SOMxVQTAM), разработанная в ходе данной работы, обучается с помощью комбинации алгоритмов обучения модульной сети, а также по алгоритму обучения сетей типа VQTAM. На этапе обучения, после подачи очередного обучающего примера на вход сети, вычисляются выходы всех сетей типа VQTAM, использованных в качестве модулей, далее определяется модуль-победитель как модуль, выход которого минимально удален от ожидаемого выхода сети на представленном обучающем примере. После этого происходит подстройка весов сети типа VQTAM, находящейся в модуле-победителе, подстройка весов происходит по алгоритму подстройки весов сетей типа VQTAM. Далее набор весов данной сети рассматривается как один весовой вектор модуля-победителя модульной карты, и происходит подстройка весов модульной карты по стандартным алгоритмам подстройки весов, применяемых при обучении нейронных карт Кохонена.

В случае с модульной сетью, где в качестве модулей применены сети типа RSOM (то есть сеть SOMxRSOM), также полученной в ходе данной работы, обучение происходит аналогичным образом.

Далее рассмотрены некоторые примеры работы полученных новых нейронных сетей на ряде реальных данных и произведено сравнение с некоторыми другими алгоритмами.

Применение нейронных сетей на основе карт Кохонена
для идентификации динамических объектов

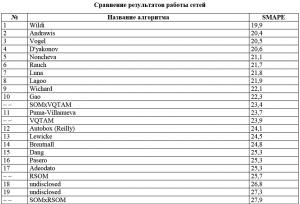
Для экспериментов и сравнительного анализа алгоритмов сети типов VQTAM, RSOM, SOMxVQTAM и SOMxRSOM были запущены на выборках, использовавшихся в 2008 году для определения победителей на соревновании нейросетевых алгоритмов прогнозирования [15]. Результаты этого соревнования были использованы в данном исследовании, так как в них детально описана методика определения места в таблице результатов, к тому же в соревновании приняли участие большое число различных алгоритмов прогнозирования, присутствуют описание работы большинства из этих алгоритмов, а также выборки данных, на которых производилось тестирование этих алгоритмов, что позволяет провести сравнительный анализ описываемых в данной статье нейросетевых алгоритмов с другими передовыми методиками. Для определения места в таблице результатов организаторами данного соревнования [15] было предложено провести прогноз на 56 шагов для каждой из 111 выборок. Для каждого из полученных прогнозов рассчитывалась симметричная средняя абсолютная процентная ошибка (Symmteric Mean Absolute Percent Error – SMAPE):

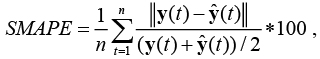
где y(t) – реальное состояние объекта в момент времени t; 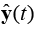 – выход модели в момент времени t; n – число точек в тестовой выборке (56 в данном соревновании). Затем место в таблице определялось по средней по всем 111 выборкам ошибке (см. таблицу).

Каждая из 111 выборок имела различную длину (выборки, представляющие собой ежемесячные и ежедневные измерения ряда экономических показателей).

Пример работы сетей на одной из 111 выборок

Для примера возьмем одну из 111 выборок и рассмотрим результаты обучения каждого из четырех представленных в данной работе типов сетей. В итоге приходим к предположению, что модульные модификации сетей приводят к значительному снижению ошибки в случае применения модулей типа VQTAM, но, с другой стороны, модульные сети значительно более чувствительны к изменению параметров обучения. Более высокая ошибка SMAPE модульных сетей типа SOMxRSOM по сравнению с сетями типа RSOM может быть объяснена тем, что RSOM-сети сами по себе содержат локальные модели, и во время процесса обучения SOMxRSOM-сети эти локальные модели рассматриваются как весовые векторы всей SOMxRSOM-сети, но локальные модели построены для различных участков входных данных (из-за различия весовых векторов RSOM, использующихся в качестве модулей), поэтому локальные модели, соответствующие нейронам на одной и той же позиции в картах разных RSOM, в общем случае построены для разных участков входной выборки, что приводит к нарушению этих локальных моделей во время процесса подстройки весовых коэффициентов модульной сети SOMxRSOM.

Заключение

В данной работе был рассмотрен ряд нейронных сетей на основе самоорганизующихся карт Кохонена, которые могут быть успешно применены для идентификации динамических объектов различной сложности. Предложены новые модульные нейросетевые архитектуры, в качестве модулей которых использованы сети типа VQTAM и RSOM. В случае с нейронными сетями, где в качестве модулей использованы сети типа VQTAM, получено улучшение качества прогноза по сравнению с обыкновенной сетью типа VQTAM. В случае же с нейронными сетями, где в качестве модулей использованы сети типа RSOM, качество прогноза снижено по сравнению с обыкновенной сетью типа RSOM, что обосновано особенностями алгоритма построения локальных линейных моделей. Эти результаты показывают возможность улучшения качества работы нейронных сетей некоторых архитектур при объединении их в модульные сети.

Литература

1. Бессонов А.А., Загашвили Ю.В., Маркелов А.С. Методы и средства идентификации динамических объектов. М.: Энергоатомиздат, 1989. 280 с.

2. Дейч А.М. Методы идентификации динамических объектов. М.: Энергия, 1979. 240 с.

3. Мишулина О.А. Статистический анализ и обработка временных рядов. М.: Изд-во МИФИ, 2004. 180 с.

4. Хайкин С. Нейронные сети: полный курс. М.: Вильямс, 2006. 1104 с.

5. Efremova N., Asakura N., Inui T. Natural object recognition with the view-invariant neural network. Proc 5th Intern. Conf. of Cognitive Science (CoSci), 2012, pp. 802–804.

6. Трофимов А.Г., Повидало И.С., Чернецов С.А. Использование самообучающихся нейронных сетей для идентификации уровня глюкозы в крови больных сахарным диабетом 1-го типа // Наука и образование. 2010. № 5. URL: http://technomag.edu.ru/doc/142908.html (дата обращения: 06.09.2017).

7. Souza L.G.M., Barreto G.A. Multiple local ARX modeling for system identification using the self-organizing map. Proc. of European Symp. on Artificial Neural Networks – Computational Intelligence and Machine Learning. Bruges, 2010.

8. Koskela T. Neural network methods in analyzing and modelling time varying processes. Helsinki University of Technology Publ., 2003, pp. 1–72.

9. Varsta M., Heikkonen J. A recurrent self-organizing map for temporal sequence pro-cessing. Springer, 1997, pp. 421–426.

10. Lotfi A., Garibaldi J. Applications and Science in Soft Computing. Advances in Soft Computing Series, vol. 24, Springer Publ., 2003, pp. 3–8.

11. Tokunaga K., Furukawa T. SOM of SOMs. Neural Networks, 2009, no. 22, pp. 463–478.

12. Tokunaga K., Furukawa T. Modular network SOM. Neural Networks, 2009, no. 22, pp. 82–90.

13. Logothetis N.K., Pauls J., Poggiot T. Shape representation in the inferior temporal cortex of monkeys. Current Biology, 1995, no. 5, pp. 552–563.

14. Vetter T., Hurlbert A., Poggio T. View-based Models of 3D Object Recognition: Invariance to Imaging Transformations. Cerebral Cortex, 1995, no. 3, pp. 261–269.

15. Artificial Neural Network \& Computational Intelligence Forecasting Competition, 2008. URL: http://www.neural-forecasting-competition.com/NN5/results.htm (дата обращения: 06.09.2017).

16. Averkin A.N., Yarushev S. Hybrid approach for time series forecasting based on ANFIS and Fuzzy Cognitive Maps. Soft Computing and Measurements (SCM). Proc. XX IEEE Intern. Conf. on. IEEE, 2017,
pp. 379–381.