В процессе управления жизненным циклом (ЖЦ) регулярно производятся измерения технологических процессов. Подобных процессов множество, и все они взаимосвязаны. Целесообразно было бы обрабатывать полученную информацию для прогнозирования развития процессов, а применение нечетких когнитивных карт позволит выявить взаимосвязи между всеми процессами. В развитии и будущих изменениях временных рядов имеет место рефлексивность между событиями, их участниками и собственно прогнозируемым процессом (временным рядом), между исследователем и исследуемым процессом. Теория рефлексивности в экономическом мире говорит о том, что возникшая ситуация действует на поведение самих участников процесса, а их мышление и поведение действуют на развитие ситуации, участниками которого они являются. Но данная теория применима не только к экономике, она имеет место быть во всех сферах человеческой деятельности. Одним из таких примеров является задача управления ЖЦ изделия. Понятно, что, пользуясь одним лишь инструментом прогнозирования временных рядов, сколь угодно мощным бы он ни был, невозможно отразить и учесть ситуацию и события, воздействующие на исследуемый процесс, так, как, допустим, нейронная сеть работает с историческими данными. Практическим выходом из положения является разработка таких методов, которые могли бы оперировать как с причинно-следственными отношениями между событиями и прогнозируемым процессом, так и с числовыми значениями временного ряда, его историческими данными. Данная ситуация моделируется с помощью гибридной системы прогнозирования, способной оперировать и качественными данными (субъективным мнением эксперта), и количественными (характеристиками исследуемого процесса).
Таким образом, представляется актуальной разработка новых гибридных моделей прогнозирования и анализа временных рядов, основанных на методах когнитивного моделирования, нечеткой логики и искусственных нейронных сетей.
В настоящей работе предлагается гибридный подход к разработке систем прогнозирования временных характеристик процессов для задач управления ЖЦ изделий, основанный на модулярной архитектуре построения систем прогнозирования и базирующийся на гибридизации нейро-нечеткой нейронной сети ANFIS и нечетких когнитивных картах. С помощью подобной гибридной архитектуры система прогнозирования способна оперировать как качественными данными (субъективными мнениями экспертов), так и количественными (характеристиками исследуемого процесса). Остановимся подробнее на модуле с нечеткой когнитивной картой. Для облегчения задачи настройки весов когнитивной карты используем генетический алгоритм для обучения когнитивной карты, благодаря чему она способна самостоятельно обучиться и производить настройку.
Обзор моделей ЖЦ
Для разработки системы, способной качественно и продуктивно работать, необходимо исследовать область, применительно к которой разрабатывается система прогнозирования. Далее приведем модели ЖЦ технических систем.
Р ассмотрим последовательную, последовательно-параллельную, инкрементальную и спиральную модели ЖЦ. Классическая последовательная (водопадная) модель (рис. 1а), опирающаяся на ГОСТ 34.601-90, широко используется в проектно-конструкторской и производственной деятельности. В ней этапы идут один за другим: каждый новый этап начинается только после окончания предыдущего.
Главными преимуществами этой модели являются простота и легкость ее понимания и использования, поскольку отсутствуют итерации и параллельно выполняемые задачи; она хорошо работает для небольших проектов и структурированного окружения. В то же время данная модель плохо работает со сложными и долгосрочными проектами, а также в условиях быстро меняющихся требований; она не поддерживает большого числа пересматриваемых решений.
Уменьшение сроков проектирования и производства в рамках ЖЦ сложных технических систем (СТС) может быть достигнуто благодаря частичному запараллеливанию отдельных этапов проектирования и производства (в русле совмещенной разработки) (рис. 1б) [1, 2].
В целом моделирование связей между этапами и стадиями ЖЦ СТС может опираться на базовые отношения между временными интервалами, лежащие в основе логики Аллена [3] (см. таблицу).
В темпоральной логике Аллена в качестве временных примитивов используются интервалы. Здесь временной интервал a есть упорядоченная пара (a-, a+), такая, что a- < a+, где a- и a+ рассматриваются как моменты времени (например, на вещественной оси). Структура времени может быть любой (например, линейной или ветвящейся) в зависимости от конкретной ситуации [4, 5].
Интервальной интерпретацией называется функция, отображающая временной интервал на числовую ось. Множество базисных интервальных отношений BTR определяется через отношения между концами интервалов (см. таблицу).
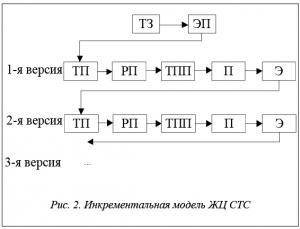
Инкрементальная модель также подразумевает линейную последовательность стадий ЖЦ, но предусматривает несколько инкрементов (версий) с запланированным улучшением продукции (рис. 2).
Достоинства и недостатки этой стратегии такие же, как и у классической (последовательной). Но, в отличие от классической модели, в данном случае заказчик может раньше увидеть результаты. Уже по результатам разра-ботки и внедрения первой версии он может незначительно изменить требова-ния к разработке, отказаться от нее или предложить разработку более совершен-ного продукта с заключением нового договора.
С одной стороны, последовательная и инкрементальная модели ЖЦ могут порой трактоваться как локальные фрагменты круговой модели, с другой – усиление достоинств и компенсация недостатков линейной и круговой моделей в отдельности достигается путем их интеграции и построения синтетической, спиральной модели ЖЦ. Итеративный характер процессов и работ на протяжении ЖЦ СТС адекватно отражается с помощью спиральной модели. При этом обеспечивается возможность перехода на следующий этап ЖЦ, не дожидаясь окончания предыдущего этапа. Более того, недостающую работу можно выполнить на следующей итерации.
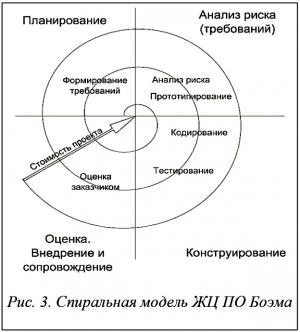
Наиболее известной спиральной моделью ЖЦ считается модель Б. Боэма [6], появившаяся в 1986 г. Она предназначена для отображения ЖЦ ПО и предусматривает анализ рисков (рис. 3). В ней последовательность «анализ требований – проектирование – реализация – тестирование» выполняется более одного раза. Для этого может быть несколько причин, например, необходимость предупреждения рисков, возможность предоставить заказчику частичную версию проекта для получения отзывов и пожеланий.
Если разрабатываемая программа достаточно сложна, необходимо выполнять промежуточные итерации, не откладывая эту фазу на самый конец, как это предписывает водопадная модель.
Общая идея спирального процесса заключается в том, чтобы на каждой итерации строить очередную версию программы, используя в качестве основы ее предыдущую версию. В этом случае процесс приобретает спиралевидный характер.
Необходимо отметить, что исторически более ранней и существенно более детальной была спиральная модель ЖЦ [7].
Управление ЖЦ изделия
Управление ЖЦ СТС означает интеграцию данных, процессов, структур, персонала ряда предприятий в рамках единой корпоративной сети [8].
Его ключевые аспекты:
– безопасный и управляемый доступ к информации о создаваемой системе, а также ее совместное использование в спецификации СТС;
– обеспечение согласованности информации о СТС на протяжении всего ЖЦ;
– поддержка процессов создания, управления, распространения, разделения и использования информации о СТС.
С одной стороны, одной из главных подсистем системы управления ЖЦ продукции является система управления данными о продукции PDM (Product data management). Сегодня PDM-система в достаточно полном объеме реализует функции управления составом СТС, структурой всех ее составных частей, деталей, узлов и агрегатов. Кроме того, сюда должны входить и структурированные информационные объекты технологической подготовки производства, состав которых отражает все необходимые данные для организации работ по производству самого изделия, структуру оснастки, инструментального парка, операций и переходов, технологических приемов. Задачи управления данными об СТС и управления работами по созданию СТС являются взаимосвязанными и должны базироваться на единых информационных ресурсах. При этом важное место занимает построение системы управления проектом, основная задача которой состоит в координации действий исполнителей проекта, в обеспечении согласованного планирования и контроля работ, в предоставлении необходимой информации о ходе выполнения проекта. Интеграцию данных на различных этапах ЖЦ удобно осуществлять на основе семантического подхода, опирающегося на онтологическое описание проблемной области в терминах теории множеств и алгебраических систем.
С другой стороны, важнейшей подзадачей задачи управления ЖЦ СТС является управление знаниями, циркулирующими на его этапах и стадиях. Управление знаниями на протяжении ЖЦ – это инновационная стратегия работы предприятия, направленная на обмен знаниями как ресурсами, коллективно используемыми на разных этапах ЖЦ, получение новых и обновление существующих знаний, позволяющих сотрудникам лучше понимать друг друга, эффективно взаимодействовать и совместно решать сложные задачи. Оно обеспечивает единый интегрированный подход к созданию, сбору, организации, распределению, использованию информационных ресурсов предприятия и доступу к ним. Эти ресурсы включают структурированные БД, документы, неявные знания сотрудников.
В конце XX–начале XXI вв. возникла концепция инженерии ЖЦ, которая предполагает широкое использование современных информационных и коммуникационных технологий в моделировании и интеграции его этапов. Главными аспектами инженерии ЖЦ выступают инженерия знаний и управление знаниями о ЖЦ, в частности, на основе наглядного представления его структуры, оптимизация временных соотношений между этапами и стадиями ЖЦ СТС (например, сокращение сроков проектирования и увеличение периода эксплуатации СТС), учет и управление неопределенностями, возникающими на разных этапах ЖЦ.
Модулярная гибридная система прогнозирования временных рядов
Для разработки качественной системы прогнозирования был проведен анализ нейросетевых гибридных подходов к прогнозированию временных рядов [9]. Как показывают исследования, наиболее качественные прогнозы получаются при помощи нейро-нечетких сетей. Все связано с тем, что в большинстве исследуемых процессов имеет место нечеткая природа. Оперировать нечеткими данными можно благодаря понятию нечеткого множества [10]. Применяя подобное понятие, можно формализовать лингвистическую информацию, на основе которой в дальнейшем строить математические модели [11, 12]. Используемые в системе прогнозирования нечеткие когнитивные карты основаны на теории, предложенной в [13].
На основе данных теорий, методов и результатов анализа была разработана модулярная система прогнозирования. Подробно она рассматривается в [14]. Задача прогнозирования на основе нечеткой когнитивной карты определяется, согласно [15] и [16], как задача определения приращений концептов, возникающих в карте при внесении в нее «возмущений» – изначального вектора приращений концептов.
Прогнозирование на основе разработанной гибридной модели имеет две основные стадии. На первой стадии разрабатывается модель нечеткой когнитивной карты по историческим данным временных рядов, используя генетический алгоритм обучения. На второй используются концепты нечеткой когнитивной карты для определения входов для нейро-нечеткой сети для повышения точности прогнозирования. Подробно стадии описаны в [17].
Прогнозирование временных характеристик ЖЦ
Для тестирования разработанной системы использовались несколько показателей, а именно, стоимость и продолжительность ЖЦ в производстве самолетов Boeing и Airbus [18].
На продолжительность влияют такие показатели, как длительность каждой стадии, возможные поломки, нештатные ситуации, отклонение от графика, сбои в производстве, а также доступность ресурсов и возможные ошибки. Многие из данных показателей имеют свою определенную степень нечеткости, это приводит к выводу, что использование теории нечеткой логики является самым правильным решением для работы в такой ситуации. Исходя из проведенного анализа методов прогнозирования, а также из приведенных выше фактов и было принято решение о разработке гибридной системы прогнозирования, в основе которой лежат нечеткие когнитивные карты и нейро-нечеткая сеть.
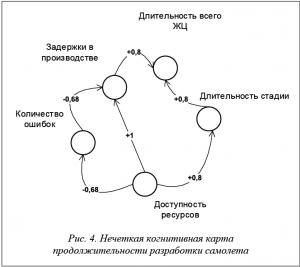
Для начала представим нечеткую когнитивную карту, отражающую влияющие стадии и факторы. Нечеткая когнитивная карта, отражающая факторы, влияющие на продолжительность ЖЦ, представлена на рисунке 4.
Благодаря построению нечеткой когнитивной карты есть возможность наглядно увидеть факторы, влияющие на продолжительность, что, в свою очередь, позволяет принимать верные управленческие решения для оптимизации процессов. Далее модуль, отвечающий за процесс прогнозирования на основе нечеткой когнитивной карты, получает данные из вершин и дает так называемый качественный прогноз, то есть прогноз, основанный на субъективных знаниях эксперта. Описание получения прогноза и обучения нечеткой когнитивной карты дано выше.
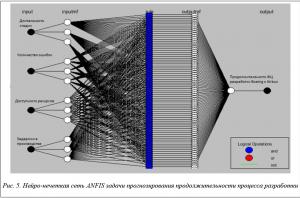
Нейро-нечеткая сеть ANFIS задачи прогнозирования временных характеристик ЖЦ на примере прогноза продолжительности процесса разработки самолета Boeing представлена на рисунке 5.
Как видно из структуры сети, на вход подаются факторы, наибольшим образом влияющие на продолжительность прогнозируемого процесса. Разработанная модель имеет довольно гибкую структуру и позволяет учитывать любое количество факторов, на основе которых возможно сделать прогноз. Благодаря использованию именно нечеткой нейронной сети появляется возможность экспертным путем вносить дополнительные правила в работу нейронной сети, чтобы она наиболее точным образом воспринимала данные обучающей выборки и давала адекватный прогноз. Полученный прогноз можно видеть на рисунке 6. Как известно, на практике разработка, опытное производство и летные испытания нового самолета занимают в среднем 5,4–6,8 лет. Для прогноза авторы выполнили нормировку данных, в рассматриваемом случае 5,4 года – это 64 месяца. Для работы был использован набор временных данных.
Как видно из графика, прогноз, получаемый в результате работы системы, довольно точно работает. Однако видна проблема в крайне неравномерном распределении временных затрат в зависимости от месяца и стадии соответственно. Благодаря тому, что имеется и когнитивная карта ситуации, есть возможность принять наиболее точные управленческие решения и оптимизировать работу, некоторые стадии организовать параллельно, что позволит сократить временные затраты, а следовательно, и финансовые.
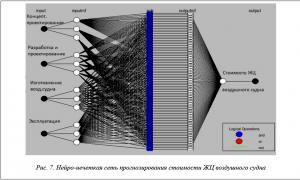
Далее рассмотрим пример прогноза стоимости ЖЦ воздушного судна. На данный показатель влияет большое количество факторов: концептуальное проектирование, непосредственная разработка и проектирование, изготовление воздушного судна, эксплуатация, ремонт и обслуживание, утилизация. Данные факторы являются составляющими стоимости ЖЦ воздушного судна. На рисунке 7 представлена сеть ANFIS для прогнозирования стоимости ЖЦ.
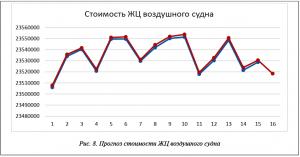
В дальнейшем целесообразно разрабатывать системы прогнозирования для каждого фактора отдельно, так как все они включают в себя определенные стадии и этапы, для которых возможно разработать когнитивные карты. На рисунке 8 представлен график прогнозных показателей стоимости ЖЦ воздушного судна.
Как видно из данного графика, стоимость ЖЦ также имеет довольно заметные скачки. Дальнейшая экспертная работа с использованием разработанной системы даст возможность решить данную проблему, так как нечеткие когнитивные карты позволяют увидеть всю ситуацию наглядно и отследить взаимосвязи между факторами влияния.
Заключение
Данная работа представляет собой исследование в области прогнозирования временных рядов на основе нейросетевых и когнитивных методов для задачи прогнозирования временных характеристик в управлении ЖЦ изделия. Детально рассмотрены нейро-нечеткие методы прогнозирования, представлен обзор наиболее успешных работ в данной области. Исследованы проблемы в области прогнозирования временных рядов, существенным образом влияющие на качество прогнозов. Разработана гибридная модель прогнозирования, сочетающая в себе нейро-нечеткие нейронные сети и нечеткие когнитивные карты. Благодаря сочетанию столь разных методов можно добиться качественного прогнозирования тогда, когда происходят сильные скачки во временном ряде и одна нейронная сеть неспособна выполнять задачу достойным образом.
Система апробирована для задачи прогнозирования временных характеристик в управлении ЖЦ изделия на примере прогноза продолжительности и стоимости ЖЦ. Результаты тестирования позволили не только получить прогноз и проверить работоспособность системы, но и выявить проблемы внутри организации стадий разработки воздушного судна. Использование нечетких когнитивных карт позволяет увидеть ситуацию более детально, выявить факторы, наиболее влияющие на исследуемый процесс, и принять правильные управленческие решения. В данной ситуации целесообразно использовать методологию Concurrent engineering, которая позволяет устроить задачи параллельно, что, в свою очередь, позволит сократить и оптимизировать трудозатраты. Дальнейшие исследования будут направлены на оптимизацию процесса разработки нечетких когнитивных карт, а также более детальное тестирование на большем количестве факторов.
Работа выполнена при поддержке РФФИ, грант № 17-37-50013.
Литература
1. Handbook of life-cycle engineering: concepts, tools and techniques. Molina A., Sanchez J.-M. and Kusiak A. (eds.). London: Chapman and Hall Publ., 1998.
2. Tarassov V.B., Kashuba L.A., Cherepanov N.A. Concurrent Engineering and AI Methodologies: Opening New Frontiers. Proc. IFIP Intern. Conf. on Feature Modeling and Recognition in Advanced CAD/CAM Systems, 1994, vol. 2, pp. 869–888.
3. Allen J.F. Maintaining Knowledge about Temporal Intervals. Communications of the ACM, 1983,
vol. 26, pp. 832–843.
4. Еремеев А.П., Троицкий В.В. Методы представления временных зависимостей в интеллектуальных системах поддержки принятия решений // Изв. РАН: Теория и системы управления. 2003. № 5.
С. 75–88.
5. Еремеев А.П., Троицкий В.В. Представление временных ограничений в интеллектуальных системах: обзор // Искусственный интеллект в XXI веке (ICAI'2001): тр. Междунар. конгр. М.: Наука, Физматлит, 2001. Т. 1. С. 61–74.
6. Boehm B. A Spiral model of software development and enhancement. ACM SIGSOFT Software Engineering Notes, 1986, vol. 11, no. 4, pp. 14–24.
7. Кашуба Л.А. Параллельное проектирование средствами CAE/CAD/CAM в жизненном цикле изделий машиностроения // Программные продукты и системы. 1998. № 3. С. 24–30.
8. Хаит Л., Солдатов В., Егошин Е., Сошин Д., Ямалов Р. Автоматизированные информационно измерительные системы испытаний авиационных двигателей/ // Современные технологии автоматизации. 1999. № 1. C. 12–16.
9. Averkin A.N., Yarushev S.A. Review of studies on time series forecasting based on hybrid methods, neural networks and multiple regression // Программные продукты и системы. 2016. №. 1. С. 75–82 (англ.).
10. Беллман Р., Заде Л. Принятие решений в расплывчатых условиях. В кн.: Вопросы анализа и процедуры принятия решений. М.: Мир, 1976. С. 172–215.
11. Ротштейн А.П., Штовба С.Д. Нечеткая надежность алгоритмических процессов. Винница, 1997. 142 с.
12. Аверкин А.Н., Батыршин И.З., Блишун А.Ф., Силов В.Б., Тарасов В.Б. Нечеткие множества в моделях управления и искусственного интеллекта. М.: Наука, 1986. 312 с.
13. Kosko B. Fuzzy cognitive maps. Intern. J. of Man-Machine Studies, 1986, vol. 24, no. 1, pp. 65–75.
14. Ефремова Н.А., Аверкин А.Н., Ярушев С.А. Гибридные нечеткие когнитивные карты в задачах поддержки принятия решений и прогнозирования // Программные продукты, системы и алгоритмы. 2017. № 4. URL: http://swsys-web.ru/hybrid-fuzzy-cognitive-maps-in-decision-support-tasks.html (дата обращения: 08.06.2018). DOI: 10.15827/2311-6749.25.291.
15. Sadiq R., Kleiner Y., Rajani B. Interpreting fuzzy cognitive maps (FCMs) using fuzzy measures to evaluate water quality failures in distribution networks. Proc. Joint ICCCBE XI, Montreal, QC, 2006, pp. 1–10.
16. Zhenbang Lu, Lihua Zhou. Advanced fuzzy cognitive maps based on OWA aggregation. Intern. J. of Comput. Cogn., 2007, vol. 5, no. 2, pp. 31–34.
17. Averkin A.N., Yarushev S. Hybrid approach for time series forecasting based on ANFIS and fuzzy cognitive maps. Proc. 2017 XX IEEE Intern. Conf. SCM, 2017, pp. 379–381.
18. Володин С.В. Управление фазами жизненного цикла проектов в наукоемкой отрасли // Вестн. Воронеж. гос. ун-та. Сер. Экономика и управление. 2013. №. 2. С. 39–47.



Комментарии