Одной из важнейших задач проектирования СБИС является задача размещения элементов на коммутационном поле (КП). В существующих алгоритмах [1], с одной стороны, связь между этими задачами недостаточно глубока, с другой, получаемые решения с точки зрения их оптимальности, как правило, неудовлетворительны. Приведенные в работе [1] обзор, сравнение и анализ разработанных алгоритмов размещения показывают, что для создания эффективного алгоритма, отвечающего современным требованиям, необходимы новые технологии и подходы. Для сокращения времени решения задач размещения используются различные эвристические способы ограничения перебора, основанные на математических закономерностях, позволяющих сократить временную и пространственную сложность алгоритма [2].
В последнее время для решения различных сложных задач, к которым относятся и задачи размещения, все чаще используются способы, основанные на применении методов искусственного интеллекта [2, 3]. Особенно стремительно растет интерес к разработке алгоритмов, инспирированных природными системами [3].

Одним из новых направлений таких методов являются мультиагентные методы интеллектуальной оптимизации, базирующиеся на моделировании коллективного интеллекта [4, 5]. Оптимизация с использованием роя частиц (Particle Swarm Optimization, PSO) – это метод поиска, который базируется на понятии популяции и моделирует поведение птиц в стае и косяков рыб [6, 7]. Рой частиц может рассматриваться как многоагентная система, в которой каждый агент (частица) функционирует автономно по очень простым правилам. В таких случаях говорят о роевом интеллекте (Swarm intelligence).

В работе излагается метод решения задачи размещения на основе роевого интеллекта [6] и генетической эволюции [8]. Предложена композитная архитектура многоагентной системы бионического поиска.

Основные положения

Пусть даны множество элементов А={a_j|j=1, 2, …, n} и множество позиций П={п_i|i=1, 2, …, с} на КП. В качестве модели схемы используется гиперграф Н=(X,E), где X={x_i|i=1, 2, …, n} – множество вершин, моделирующих элементы; E={ e_j|e_jX, j=1, 2, …, m} – множество гиперребер, моделирующих цепи, связывающие элементы. Для размещения всех элементов необходимо выполнение условия с >= n. Произвольное размещение элементов в позициях представляет собой перестановку Р=р(1), р(2), …, р(i), …, р(с), где р(i) задает номер элемента, который назначен в позицию п_i. В зависимости от выбранного критерия для оценки результатов размещения вводится целевая функция F(P). Задача размещения состоит в отыскании оптимального значения функции F на множестве перестановок Р. Для более полного учета связей между задачами размещения и трассировки используется критерий, основанный на оценках числа цепей, пересекающих заданные линии КП. Эти линии могут быть либо прямыми, пересекающими все КП, либо замкнутыми и ограничивающими некоторую область.

Пусть на КП наложена опорная сетка. Множество ребер сетки G={ g_i|i=1, 2, …, n_g} разбивает КП на дискреты. Будем считать, что позиции п_i располагаются внутри дискретов. В качестве исходных данных для КП задается множествоD={d_i|i=1, 2, …, n_d}, где d_i – пропускная способность ребра g_i, то есть число цепей (трасс), которые могут ее пересечь. Значения d_i определяются размерами ребра и ограничениями на прокладку соединений.

Назовем цикл L_k, составленный из ребер сетки G и ограничивающий некоторую область, границей области. Под пропускной способностью PS_k границы L_k будем понимать суммарную пропускную способность ребер сетки, входящих в состав L_k, то есть

Обозначим Н_к число цепей, связывающих элементы, расположенные внутри области, ограниченной L_k, с элементами, расположенными вне этой области. Введем характеристику границы:

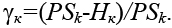
Чем большее значение имеет 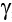_к, тем легче осуществить прокладку связей через границу L_k.

Пусть заданы некоторое размещение элементов и некоторое множество областей, для которых определены множества границ L={ L_k|k=1, 2, …, k_L}. Найдем среди характеристик границ наименьшую 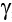_min, то есть

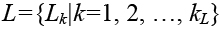. Величина F = 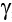_min используется в качестве критерия оптимизации. Задача оптимизации – максимизация 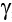_min.

Общая структура представления решений в алгоритме размещения
на основе роевого интеллекта и генетического поиска

В эвристических алгоритмах роевого интеллекта многомерное пространство поиска населяется роем частиц [6]. Каждая частица представляет некоторое решение, в данном случае – решение задачи размещения. Процесс поиска решений заключается в последовательном перемещении частиц в пространство поиска. Позиция частицы i в пространстве решений в момент времениt (t имеет дискретные значения) определяется вектором x_i(t). По аналогии с эволюционными стратегиями рой можно трактовать как популяцию, а частицу как индивида (хромосому). Это дает возможность построения гибридной структуры поиска решения, основанной на сочетании генетического поиска с методами роевого интеллекта. Связующим звеном такого подхода является структура данных, описывающая в виде хромосомы решение задачи. Если в качестве частицы используется хромосома, то число параметров, определяющих положение частицы в пространстве решений, должно быть равно числу генов в хромосоме. Значение каждого гена откладывается на соответствующей оси пространства решений. В этом случае возникают некоторые требования к структуре хромосомы и значениям генов. Значения генов должны быть дискретными и независимыми друг от друга, то есть хромосомы должны быть гомологичными.

В работе предлагается подход к построению структур и принципов кодирования хромосом, обеспечивающих их гомологичность и возможность одновременного использования в генетическом алгоритме и в алгоритме на основе роя частиц.

Как уже указывалось, размещение элементов в позициях задается перестановкой элементов P={p_i|i= 1, 2, …, n}. Хромосома, соответствующая решению Р, состоит из генов, число которых на единицу меньше числаn элементов в векторе P. H={ g_j|j=1, 2, …, (n–1)}. Возможные значения гена зависят от локуса и меняются в интервале 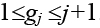. Решение Р получается путем применения к хромосоме рекурсивной процедуры декодирования.

Построение вектора Р производится последовательно с использованием опорного вектора B={b_i|i=1, 2, …, n}. Обозначим через P_j частично построенный вектор размещения на шаге j. На каждом шаге j строится вектор P_j+1 путем включения в P_j элемента b_j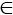B. Место включения b_j в P_j определяется в результате декодирования гена g_j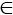H. Окончательно вектор Р будет построен на шаге n, то есть P=P_n. Вначале принимается, что P₁={b₁}, то есть P ₁ включает первый элемент b₁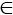B. Пусть P_j={p_i^j|i=1, 2, …, t}. Тогда P₁={p₁¹}, P₂={p₁²,p₂²}, P₃={p₁³,p₂³,p₃³} и т.д. На каждом шаге j декодирования хромосомы строитсяP_j+1. Для этого выбирается генg_j и определяется место i=g_j включения элементаb_j+1 в вектор P ₂. P_j+1 получается путем вставки в P_j элемента b_j+1 после p^j_i-1 и сдвига на одну позицию элементов p^j_i-1+k, k=1, 2, …, (j-i). Связь между элементами p_l^j и p^{j+ 1}_l определяется с помощью следующих выражений:

p_l^{j+ 1} =p^j, l= 1, 2, …, (i-1); p_i^j+1=b_t+1; p_i+k^j+1= p^j_i-1+k , k=1, 2, …, (j-i).

Рассмотрим метод декодирования на примере. Пусть имеются хромосома H=<1, 2, 2, 1> и опорный вектор B=<2, 3, 1, 5, 4>. Вначале принимаем, что P₁={b₁}={ p₁¹}={2}.

На первом шаге строится P₂ путем включения b ₂=3 в P₁. Для этого рассматривается ген g₁, i=g₁=1. Отсюда p²_i=p²₁=b₂=3; p²₂=p¹ ₁=2. Итак, P₂={3,2}.

На втором шаге строится P₃ путем включения b₃=1 в P₂. Рассматривается генg₂, i=g₂=2. Отсюда p₁³=p²₁=3; p_i³=p₂³=b₃=1; p₃³=p₂²=2. Итак, P₃={3,1,2}.

На третьем шаге строится P₄ путем включения b₄=5 в P₃. Рассматривается ген g₃. i=g₃=2. Следовательно, p₁⁴=p₁³=3; p_i⁴=p₂⁴=5; p₃⁴=p₂³=1; p₄⁴=p₃ ³=2. Отсюда P₄={3,5,1,2}.

На четвертом шаге строится P₅ путем включения b₅=4 в P₄. Рассматривается ген g₄, i=g₄=1. Следовательно, p_i⁵=p⁵₁=4, p₂⁵=p₁⁴=3, p₃⁵=p₂⁴=5, p₄⁵=p₃⁴=1, p₅⁵=p₄⁴=2. Окончательно P=P ₅={4,3,5,1,2}.

Фенотип, то есть решение задачи размещения, получается после декодирования хромосом и построения вектора P. При размещении одногабаритных элементов значением p_i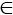P является номер элемента, размещаемого в i-й позиции. При размещении разногабаритных элементов вектор P задает порядок, в котором элементы укладываются на плоскости.

Алгоритм размещения на основе роевого интеллекта

Основу поведения роя частиц составляет самоорганизация, обеспечивающая достижение общих целей роя на основе низкоуровневого взаимодействия. Каждая частица связана с роем, может взаимодействовать со всем роем и тяготеет к лучшему решению роя. Процесс поиска решений итерационный. На каждой итерации каждая частица перемещается в новую позицию. Новая позиция определяется как

x_i (t+1)=x_i(t)+ v_i(t+1),

где v_i(t+1) – скорость перемещения частицы из позиции x_i(t) в позицию x_i(t+1). Начальное состояние определяется как x_i(0), v_i (0) [6].

Приведенная формула представлена в векторной форме. Для отдельного измерения j пространства поиска формула примет вид:

x_ij (t+1)=x_ij(t)+ v_ij(t+1), (1)

где x_ij(t) – позиция частицы i в измерении j; v_ij(t+1) – скорость частицы i в измерении j.

Введем обозначения:

f _i (t) – текущее значение целевой функции частицы i в позиции x_i(t);

x^* _i (t) – лучшая позиция частицы i, которую она посещала с начала первой итерации, а f^* _i(t) – значение целевой функции в этой позиции (лучшее значение частицы i);

F (t) – лучшее значение целевой функции среди частиц роя в момент времени t, а x(t) – позиция с этим значением.

Тогда скорость частицы i на шаге (t+1) в измерении j вычисляется как

v_ij (t+1)=w∙v_ij(t)+k₁∙rnd(0,1)∙(x^*_ij(t)-x_ij(t))+k₂∙rnd(0,1)∙( x_j(t)-x_ij(t)),           (2)

где rnd(0,1) – случайное число на интервале (0,1), ( w, k₁, k₂) – некоторые коэффициенты. Формула для расчета скорости составлена из трех компонентов.

Предыдущая скорость v_ij(t) выступает в роли памяти частицы об ее перемещениях в прошлом и является инерционным компонентом.

Значение второго компонента, называемого когнитивным, прямо пропорционально текущему расстоянию частицы от ее наилучшей позиции, которая была найдена с момента старта ее жизненного цикла. Когнитивный компонент выступает в роли индивидуальной памяти о наиболее оптимальных позициях данной частицы.

Значение третьего компонента, называемого социальным, прямо пропорционально текущему расстоянию частицы от наилучшей позиции роя в момент времени t. Благодаря социальному компоненту частица имеет возможность передвигаться в оптимальные позиции, найденные соседними частицами.

В нашем случае позиция x_i(t) задается с помощью хромосомы H_i(t)={ g_ij|j=1, 2, …, (n-1)}, структура которой рассмотрена выше. Отметим, что скоростьv_i(t) имеет ту же структуру, что и хромосома H_i(t). Позиция x_i(t), то есть хромосома H_i(t), является решением, а скорость v_i(t+1) рассматривается как средство изменения хромосомы, то есть решения.

Отличительной особенностью позиции x_i( t)=H_i(t) является то, что возможные значения гена g_ij зависят от локуса и меняются в интервале 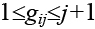. Обозначим какxc_i(t) и vc_i(t) позицию и скорость, для которых выполняются указанные выше ограничения. Рассмотрим методику получения xc_i(t) и vc_i(t). Расчет выполняется в два этапа. Вначале рассчитывается v_ij(t+1).

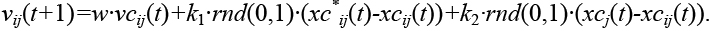        (3)

Затем по v_ij(t+1) рассчитывается vс_ij(t+1).

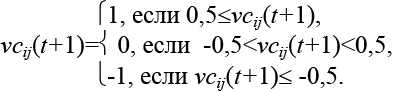                                                     (4)

Новая позиция вычисляется следующим образом.

Вначале рассчитывается

x_ij (t+1)= xс_ij(t) + vс_ij(t+1).                    (5)

Затем определяется позиция с целочисленным значением, заключенным в заданном диапазоне.

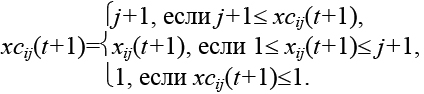
Схема работы роевого алгоритма размещения включает следующие шаги.

1. В соответствии с постановкой задачи размещения и исходными данными формируется структура данных частицы (хромосома) и устанавливаются диапазоны значений для каждого измерения (оси) пространства поиска.

2. Создается исходная случайная популяция частиц, t=0. Для каждой частицы случайным образом задаются начальная позицияxc_i(0) и начальная скорость перемещения vc_i(0). С этой целью в каждой формируемой хромосоме, соответствующей позиции xc_i(0), каждому гену, лежащему в локусе j, случайным образом присваивается целочисленное значение, лежащее в диапазоне . Генам хромосомы, соответствующей скорости перемещения vc_i(0), задаются сравнительно малые значения.

3. Вычисляется t= t+1.

4. Рассчитывается целевая функция f_i( t) для каждой частицы.

5. Для каждой частицы определяются лучшая позиции xc^* _i(t+1), которую она посещала с начала первой итерации, и значение целевой функции f^*_i(t+1) в этой позиции.

7. Определяются лучшая позиция роя на шаге t и значение целевой функции F(t) в этой позиции.

8. Лучшие частицы с точки зрения целевой функции объявляются «центром притяжения». Векторы скоростей всех частиц устремляются к этим центрам. Чем дальше частица находится от центра, тем большим ускорением она обладает. По формулам (3) и (4) для всех частиц рассчитываются скорости приращения.

9. Рассчитываются новые позиции частиц в пространстве решений.

10. Шаги 3–9 итерационно повторяются заданное число раз.

11. Последний «центр тяжести» соответствует найденному локальному оптимуму.

Таким образом, согласно алгоритму роя, после случайной инициализации популяции частиц для каждой из них вычисляется значение целевой функции f_i(t+1). Если оно окажется лучше f^*_i(t), тоf^*_i(t+1)=f_i(t+1), в противном случае f^*_i(t+1)=f^*_i(t). Далее среди f_i(t+1) выбирается лучшее значение F(t), и затем вычисляются, согласно приведенным выше формулам, новые значения скоростей частиц и их новые позиции в пространстве решений. Итерационный процесс повторяется. Отметим, что формула (1) фактически является оператором (назовем его роевым), с помощью которого изменяется текущее решение.

Гибридизация роевого интеллекта с генетическим поиском

Предлагается композитная архитектура многоагентной системы бионического поиска для решения задачи размещения на основе роевого интеллекта [8] и генетической эволюции [8]. Рассмотрены три подхода к построению такой архитектуры.

Первый и наиболее простой подход к гибридизации заключается в следующем. Сначала поиск решения осуществляется генетическим алгоритмом [9]. Затем на основе популяции, полученной на последней итерации генетического поиска, формируется популяция для роевого алгоритма. В формируемую популяцию включаются лучшие, но отличные друг от друга хромосомы. При необходимости полученная популяция доукомплектовывается новыми индивидами. После этого дальнейший поиск решения осуществляется роевым алгоритмом.

При втором подходе метод роя частиц используется в процессе генетического поиска и играет роль, аналогичную генетическим операторам. В этом случае на каждой итерации генетического алгоритма синтез новых хромосом, с одной стороны, осуществляется с помощью кроссинговера и мутации, а с другой – с помощью операторов метода роя частиц по формулам (5) и (6) и модификации формулы (3). Модифицированная формула получается путем удаления в формуле (3) второй компоненты и имеет вид

v_ij (t+1)=w∙vс_ij(t)+k∙rnd(0,1)∙(xс_j(t)-xс_ij( t)). (7)

Третий подход – это объединение первого и третьего подходов.

Оценка временной сложности операторов роя частиц не превышает оценки временной сложности генетических операторов. Оценка временной сложности генетического алгоритма не превышает оценки временной сложности алгоритма роя частиц. В связи с этим общая оценка временной сложности при любом подходе к гибридизации не превышает оценки временной сложности генетического алгоритма и лежит в пределах О(n ²)–О(n³).

Экспериментальные исследования

Для написания программы был использован язык C++ в среде Microsoft Visual Studio 2010 для ОС Windows, так как главный упор делался на скорость работы приложения.

Тестирование проводилось на ЭВМ с процессором Intel Core 2 Duo T6600 2200 МГц, 4 Гб ОЗУ под управлением операционной системы Windows 7.

В основе методики исследований лежит синтез контрольных примеров для задачи размещения с известным оптимумом (PEKO) [10]. Набор PEKO имеется в обоих форматах GSRC BookShelf и LEF/DEF, и они доступны в сети. В соответствии с приведенной методикой формирования тестовых примеров были проведены исследования гибридного алгоритма на оптимальность и масштабируемость. В среднем программа входит в локальный оптимум на 150-й итерации. Эксперименты показали, что увеличение популяции М больше 100 нецелесообразно, так как это не приводит к заметному изменению качества. Для сравнения экспериментальных данных алгоритмов размещения были выбраны наиболее известные генетические алгоритмы GASP [11], ESP [12] и алгоритм на основе моделированного отжига TimberWolf F 4.3 [13]. Тестирование производилось на бенчмарках 19s, PrimGA1, PrimGA2. По сравнению с существующими алгоритмами достигнуто улучшение результатов на 6–7 %. Вероятность получения глобального оптимума составила 0,92. В среднем запуск программы обеспечивает нахождение решения, отличающегося от оптимального менее, чем на 2 %. Временная сложность алгоритма при фиксированных значениях M и T лежит в пределах О (n).

Заключение

Гибридный подход, способы и методы представления задачи размещения в виде эволюционных процессов, основанных на интеграции моделей адаптивного поведения биологических систем, композитных архитектур нахождения решений, позволяет работать с задачами большой размерности и получать качественные результаты за приемлемое время. Улучшение работы предложенных алгоритмов разбиения по сравнению с известными методами составило по качеству от 5 до 10 % в зависимости от вида оптимизационных задач.

Работа выполнена при финансовой поддержке гранта РФФИ № 17-07-00997.

Литература

1. Sherwani N. Algorithms for VLSI physical design automation. Boston-Dordrecht-London. Kluwer Аcad. Publ, 1995, 538 p.

2. МакКоннелл Дж. Основы современных алгоритмов. М.: Техносфера, 2004. 368 с.

3. Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой. М.: Изд-во МГТУ им. Н.Э. Баумана, 2014. 448 с.

4. Курейчик В.М., Лебедев Б.К., Лебедев О.Б. Поисковая адаптация: теория и практика. М.: Физматлит, 2006. 272 с.

5. Engelbrecht A.P. Fundamentals of Computational Swarm Intelligence. John Wiley & Sons, Chichester, UK, 2005, 672 р.

6. Clerc M. Particle Swarm Optimization. ISTE, London, UK, 2006, 244 p.

7. Poli R. Analysis of the publications on the applications of particle swarm optimization. Jour. Artificial Evolution and Applications, Article ID 685175, 2008, 10 p.

8. Емельянов В.В., Курейчик В.М., Курейчик В.В. Теория и практика эволюционного моделирования. М.: Физматлит, 2003. 432 с.

9. Курейчик В.М., Лебедев Б.К., Лебедев О.Б. Решение задачи размещения на основе эволюционного моделирования // Изв. Акад. наук. Теория и системы управления. 2007. № 4. С. 78–90.

10. Cong J., Nataneli G., Romesis M., and Shinnerl J. An area-optimality study of floorplanning. Proc. of the Intern. Sympos. Physical Design, Phoenix, AZ, 2004, pp. 78–83.

11. Eisenmann H. and Johannes F.M. Generic Global Placement and Floorplanning. DAC, 1998, pp. 269–274.

12. Shahoolkar K. and Mazumder P. A genetic approach to standard cell placement. Proc. 1st Europ. Design Automation Conf., 1999.

13. Sechen C. and Sangiovanni Vincentelli A. The Timberwolf placement and routing package, IEEE J. Solid. State Circuits, 1995, vol. SC-20, pp. 510–522.