Оптимизация была и остается одним из наиболее трудоемких и ответственных этапов разработки ПО [1–4]. Ее роль по-прежнему значима для систем с высокими требованиями к производительности программных кодов, в том числе систем научного и военного назначения, бортового оборудования автономных транспортных средств, внедряемых систем (систем слежения и распознавания, датчиков мониторинга состояния опасных сред) и других. В рамках научного проекта разработаны модели и алгоритмы, позволившие программно реализовать средства автоматизации оптимизационных преобразований исходных кодов вычислительных систем. На первом этапе (2017 год) была разработана программная платформа, представляющая собой надстройку к среде Microsoft Visual Studio и интерфейсную оболочку, дополняющую стандартное меню среды Visual Studio новыми инструментальными средствами. В результате первого этапа были получены инструмент поиска оптимального состава подсистем (оптимальной декомпозиции), минимизирующего время работы с медленной памятью [5–7], а также непосредственно программная надстройка к MS Visual Studio (подробно с результатами первого этапа можно ознакомиться в [1]).
В данной статье подробно описаны результаты второго этапа работ, посвященного созданию моделей, методов и программных инструментов, реализующих оптимизационные подходы на основе методов экстремального программирования. Под этим понятием подразумевают нетрадиционные подходы к разработке ПО, в том числе методы оптимизации программ, основанные на улучшении одного из критериев программы за счет экстенсивного использования одного из ресурсов вычислительной системы, причем стоимость этого ресурса может быть достаточно высокой. Актуальность экстремальных методов программирования обусловлена двумя основными причинами.
Во-первых, развитие элементной базы вычислительных систем привело к значительному снижению стоимости различных компонент вычислительных систем. В результате цена единицы процессорного времени, а также стоимость хранения единицы информации (как в «быстрой» оперативной, так и в «медленной» внешней памяти) в течение нескольких лет значительно сократилась. В этих условиях использование экстремальных подходов довольно часто становится экономически оправданным. Вторая причина заключается в наличии классов задач, для которых заданные параметры качества должны быть достигнуты любой ценой (примеры подобных систем приведены в начале статьи0.
В большинстве случаев целью оптимизационных преобразований является улучшение производительности программы [7–11], а наиболее популярным вспомогательным ресурсом – оперативная память.
Одним из экстремальных оптимизационных подходов является метод, позволяющий изменить способ хранения переменных таким образом, чтобы минимизировать время обслуживания (которое составляют время выделения и освобождения блока памяти, необходимого для хранения элемента данных). Архитектура современных ОС предоставляет программам прикладного уровня три способа хранения переменных в быстрой памяти.
1. Память статическая, выделяемая единым блоком при запуске приложения, соответственно, алгоритм программы не несет никаких расходов по выделению либо освобождению памяти для статических данных. Эта область используется для размещения глобальных по времени жизни данных, то есть существующих от момента загрузки процесса до момента его завершения.
2. Стековая память, используемая для размещения временных данных, то есть переменных и массивов, объявленных в пределах любого из блоков программы. Начало блока сопровождается автоматическим выделением стековой памяти, необходимой для размещения локальных переменных. Завершение такого блока приводит к автоматическому освобождению памяти, выделенной для стековых переменных. Таким образом, для обслуживания каждой стековой переменной программа затрачивает время, необходимое на выполнение пары ассемблерных инструкций push/pop (вставка в стек выборка из стека).
3. Динамическая память позволяет выделять для работы программы участки оперативной памяти произвольного размера. Однако высокая дефрагментация динамической памяти (в случае запуска большого числа приложений) может существенно снизить скорость поиска подходящего по размеру блока. Таким образом, накладные расходы прикладного алгоритма составляет время обслуживание менеджером динамической памяти ОС всех данных программы переменной длины. Кроме того, следует учитывать, что по очевидным причинам вероятность успешного выделения динамического блока падает с ростом размера запрашиваемого участка, а также с ростом загруженности ОС. В общем случае накладные расходы на обслуживание динамической памяти значительно больше по сравнению со стековой.
Очевидно, что замена модели памяти для пользовательской переменной, заключающаяся в ее перемещении из медленной памяти в более быструю, позволит получить прирост производительности. Причем этот прирост будет более заметен на повторяющихся участках кода.
Обоснование эффективности метода оптимизации. Содержательная
и формальная постановки задачи
Высокая скорость выделения блоков памяти в стеке по сравнению с той же динамической памятью очевидна, однако процесс выделения стековой памяти занимает определенные объемы ресурсов процессорного времени. Для выявления зависимости времени выделения стека от запрашиваемого объема стека был создан тестовый код на языке С++, код которого представляет собой серию вызовов шаблонной функции f(), шаблонный параметр array_size которой используется в теле функции для создания локального массива (double x[array_size];) заданной длины. Результат каждого измерения – время 10 млн вызовов функции со стеком определенного размера. Тестовый код создан в среде MS Visual Studio 2015, однако не использует библиотеки, специфичные только для ОС Windows, – используются только функции библиотек, стандартизированных по ANSI C++ 11, то есть приведенный ниже код (листинг 1) фактически является мультиплатформенным.
Листинг 1. Исходный код тестовых замеров времени выделения стека
#include <iostream>
#include <chrono>
template<int array_size>
void f()
{
double x[array_size];
x[0] = 5; // данная строка предназначена для предотвращения..
//..удаления массива x встроенным оптимизатором
}
#define test(stack_size) start = std::chrono::system_clock::now();\
for (int i = 0; i < 10000000; i++) f<stack_size>();\
end = std::chrono::system_clock::now();\
diff = end - start;\
std::cout << "Stack allocation time: " << diff.count() << " s\n";
int main()
{
std::chrono::system_clock::time_point start, end;
std::chrono::duration<double> diff;
// замеряем время выделения стека функции...
// ... размер стека изменяется от 64000 байт (800 элементов * 8 байт..
// ... — размер типа double)...
// ... до 128000 байт (16000 элементов типа double) с шагом 64000 байт..
// ... (800 элементов).
test(800);
test(1600);
test(2400);
test(3200);
test(4000);
test(4800);
test(5600);
test(6400);
test(7200);
test(8000);
test(8800);
test(9600);
test(10400);
test(11200);
test(12000);
test(12800);
test(13600);
test(14400);
test(15200);
test(16000);
system("pause");
return 0;
}
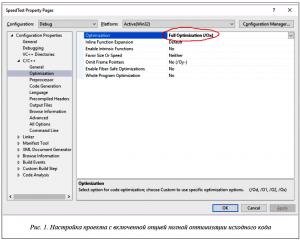
Размер стека каждого теста выбирался равным величине, кратной 64 битам, для того чтобы на производительность не влияла проблема выравнивания памяти на границу, кратной разрядности системы. Тесты проводились в конфигурации Release, причем был включен режим «Полная оптимизация» исходного кода в параметре Optimization в категории Configuration properties->C++->Optimization настроек проекта (рис. 1).
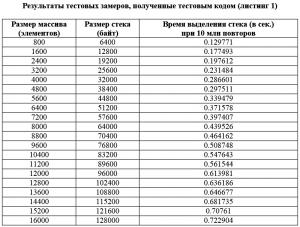
В таблице приведены усредненные экспериментальные данные, полученные по результатам 10 запусков программы.
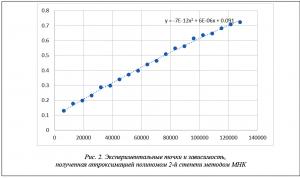
Аппроксимация экспериментальных данных методом наименьших квадратов полиномом второй степени позволила установить, что время выделения стека в зависимости от его размера носит характер практически прямой пропорциональности, так как коэффициент при x^2 стремится к нулю (рис. 2).
Результаты эксперимента и последующего анализа измерений позволяют сделать справедливые для ОС Windows и компилятора Microsoft C/C++ выводы:
– особенности реализации стековой очереди в упомянутых выше условиях (ОС/компилятор) не позволяют выделять произвольные объемы памяти за одно и то же время;
– выявлена прямая пропорциональность характера зависимости времени выделения стека от запрашиваемого размера;
– эксперименты проводились при включенной полной оптимизации в опциях компилятора, поэтому можно сделать вывод, что выявленный пропорциональный характер зависимости обусловлен в большей степени особенностью работы операционной системы и в меньшей – спецификой алгоритма компиляции.
Указанные выше выводы позволяют сформулировать положение, в соответствии с которым замена стековой переменной на статическую (то есть глобальную по времени жизни) даст очевидный прирост в производительности, пропорциональный размеру заменяемой переменной (или массива). С учетом того, что суммарный размер статических глобальных переменных увеличивает размер оперативной памяти, занимаемой программой, на некоторую постоянную величину, данный оптимизационный подход ограничен доступным клиентскому устройству объемом ОЗУ. Целевую функцию, максимизирующую суммарный выигрыш в производительности, получаемый в результате замен стековых переменных на статические, можно сформулировать в виде следующего выражения:
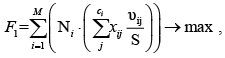 (1)
(1)
где M – число функций; – количество локальных стековых переменных, объявленных внутри блока i-й функции; Ni – количество вызовов i-й функции; S – скорость выделения стека (байт/сек.); xij – булева переменная, равная единице, если j-я локальная стековая переменная i-й функции заменяется на статическую, и нулю в противном случае; u ij – размер (в байтах) j-й локальной переменной i-й функции.
Следует отметить, что скорость выделения стека является постоянной и никак не влияет на скорость приближения к экстремуму, поэтому при расчетах ее можно либо принять равной 1 байт/сек., чтобы сохранить физический смысл значения найденного экстремума (то есть для того, чтобы размерность результата выражалась в секундах), либо множитель 1/s можно исключить из целевой функции, игнорируя тот факт, что размерность выигрыша окажется выраженной в байтах. Окончательно, с учетом упомянутого выше упрощения, а также ограничения на доступный размер оперативной памяти задачу можно представить в виде следующей дискретной [12] оптимизационной модели:
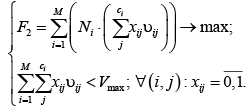 (2)
(2)
где по сравнению с моделью (1) введено новое обозначение: V max – верхняя граница доступного объема оперативной памяти, который дополнительно может быть выделен для работы программы.
В модели (2) отсутствует важное ограничение, связанное с проблемой обеспечения безопасного доступа к данным из параллельно функционирующих участков кода: Очевидно, что безопасное преобразование стековых данных в статические возможно только для такой функции, код которой ни на одном из этапов работы программы не выполняется одновременно в нескольких параллельных потоках.
Формулировка требования к потокобезопасности функции
Введем термин «блокированная переменная» для совместно используемых элементов данных, использующих механизмы синхронизации, – то есть организована безопасная работа с этими переменными в условиях многопоточности (многозадачности). Блокированной переменной считаем ту, которая заключена в блок ожидания мьютекса, семафора, события или в критическую секцию. Также введем следующие обозначения: N – количество незаблокированных переменных; M – количество одновременно выполняющихся потоков, в которых происходят чтение и запись этих переменных; R, W – матрицы размера N x M, для которых справедливо, во-первых, то, что в матрице W каждый элемент wij равен единице, если в i-ю переменную происходит запись в j-м потоке, и нулю в противном случае; во-вторых, в матрице R каждый элемент rij равен единице, если в j-м потоке i-я переменная только считывается (то есть в том же потоке нет операций записи), и нулю в противном случае. Таким образом, если в j-м потоке i-я переменная и считывается, и записывается, то rij = 0.
Ошибкой одновременного доступа являются два случая:
– когда в одну переменную запись выполняется в двух или более потоках – независимо от числа потоков чтения для этой переменной;
– когда в переменную выполняется запись только в одном потоке, но при этом количество потоков чтения этой переменной больше нуля.
Введем вспомогательные переменные:
pj – для обозначения количества потоков записи j-й переменной:
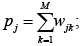 (3)
(3)
bj – для обозначения количества потоков чтения j-й переменной:
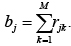 (4)
(4)
Тогда необходимость использования функций синхронизации для i-й переменной можно сформулировать в виде следующей функции:
E (j, W, R) = signum(signum(pj)(signum(bj) + signum(pj – 1))). (5)
Так как количества потоков чтения и записи для переменной – значения неотрицательные, то есть
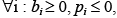 (6)
(6)
то E(j, W, R) всегда будет возвращать только два значения – ноль и единицу.
Ноль – когда ошибок синхронизации при работе с i-й переменной не было обнаружено; этому случаю соответствуют следующие сочетания значений bj и pi:
– когда bj = 0 и pj = 0;
– когда bj > 0, а pj = 0 (если нет потоков записи, то ошибки нет независимо от количества потоков чтения);
– когда bj = 0, а pj = 1 (когда нет потоков чтения, то ошибки нет, если есть только один поток записи).
Единица – в случае, когда имеет место ошибка синхронизации.
Используя указанные выше обозначения, задачу определения переменных программы, для которых имеет место ошибка синхронизации, можно сформулировать следующим образом:
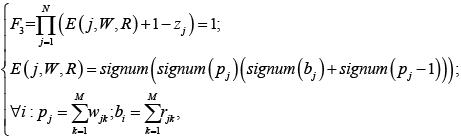 (7)
(7)
где zi – булева переменная, равная единице, если при работе с i-й переменной допущена ошибка синхронизации, и нулю в противном случае.
Неизвестными в данной модели являются булевы переменные zi. В случае, если для i-й переменной имеет место ошибка синхронизации (то есть E(i) = 1), то для компенсации этой ошибки (то есть для того, чтобы произведение F 3 стало равным 1) zi должно быть равно 1. Если же для i-й переменной ошибок синхронизации не обнаружено (то есть E(i) = 0), то zi должно быть равно единице.
Модификацию задачи (2) с учетом требования потокобезопасности можно представить в виде следующей модели:
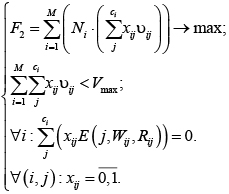 (8)
(8)
где Wij – матрица, описывающая доступ к j-й переменной i-й функции из потоков программы для записи; Rij – матрица, описывающая доступ к j-й переменной i-й функции из потоков программы для записи.
Смысл последнего ограничения заключается в том, что в каждой функции проверяются на потокобезопасность только те переменные, которые в соответствии с решением должны быть заменены на статические (то есть для которых xij = 1).
Описание программной реализации
Для автоматизации процесса поиска оптимального размещения данных в двухуровневой оперативной памяти была разработана программа «Выбор стратегии размещения пользовательских переменных в статической и стековой памяти», вошедшая в состав созданного по результатам первого этапа работ по гранту оптимизационного пакета Optimal Software Toolkit. Программа разработана на платформе .NET Framework и представляет собой форму, включающую элементы интерфейса для просмотра и редактирования исходного программного кода пользователя, ввода параметров оптимизации, вывода модифицированного кода.
Работу программы удобно проиллюстрировать на конкретном примере. Требуется выполнить оптимизацию исходного кода, текст которого приведен в листинге 2, при условии, что объем памяти, занимаемой программой, в оперативной памяти не вырастет более чем на 10 байт.
Листинг 2.
void f1()
{
int a;
float b;
}
void f2()
{
bool x;
}
void f3()
{
double c;
}
void main()
{
int k;
k=6;
f1();
if(k>5)
{
f2();
}
else
{
f1();
goto m;
}
f3();
f2();
f3();
m: f2();
}
Загрузка исходного кода в программу осуществляется двумя способами:
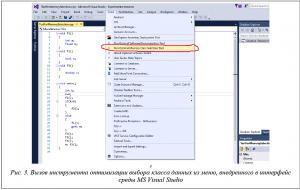
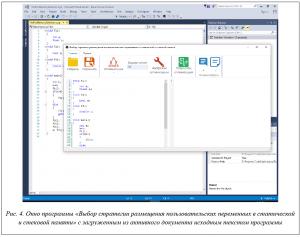
– если программа вызвана через интерфейс надстройки к MS Visual Studio Optimal Software Toolkit посредством пункта меню Tools Run Optimal Memory Class Selection Tools (рис. 2.), загрузка исходного кода будет выполнена автоматически из текущего открытого в Visual Studio файла (рис. 4).
– посредством кнопки «Открыть» на панели инструментов.
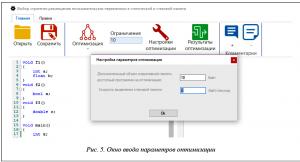
Ввод верхней границы доступных ресурсов оперативной памяти можно выполнить либо через элемент панели инструментов «Ограничение» (в верхней части рисунка 4), либо в отдельном окне «Настройки параметров» оптимизации (рис. 5), в котором, помимо верхней границы ОП, можно также задать скорость выделения стека, которая по умолчанию равна 1 – это значение не влияет на выбор оптимального плана комбинаторной задачи. Однако, если пользователю нужен отчет в единицах времени на основе реальных показателей производительности, в это поле он может ввести любые значения скорости.
После определения верхней границы доступной памяти можно приступить к выполнению оптимизации нажатием кнопки «Оптимизация». Программа анализирует исходный код, готовит предварительные данные для оптимизационной модели, в том числе выделяет все функции, подсчитывает количество вызовов каждой функции и, наконец, формирует список локальных переменных и массивов, входящих в состав каждой функции. После завершения подготовки предварительных данных на экран выводится окно промежуточных результатов анализа, содержащее список функций и количество обращений, подсчитанное анализатором для каждой функции (рис. 6). Данное окно предназначено для того, чтобы пользователь при необходимости мог скорректировать количество вызовов для той или иной функции вручную, так как на основе исходного кода не всегда можно точно определить количество обращений автоматическими алгоритмами (для пользовательских алгоритмов высокой сложности очевидным выходом из положения является ввод данных о числе вызовов, полученных при тестовом запуске оптимизируемого приложения в режиме профайлера Visual Studio).
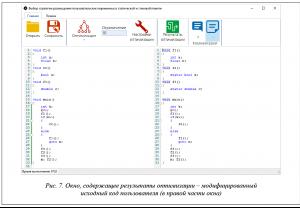
После нажатия кнопки «Продолжить оптимизацию» программа находит оптимальный план в соответствии с моделью (2) и модифицирует исходный код пользователя: для всех локальных стековых переменных, подлежащих замене на стековые, в местах объявлений добавляется ключевое слово static. Модифицированный исходный код выводится в правой части интерфейсного кона программы (рис. 7).
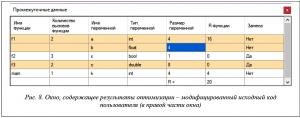
Если пользователь хочет ознакомиться с детализацией полученного решения, он может воспользоваться кнопкой «Результаты оптимизации» на панели инструментов. При этом на экран будут выведены результаты вычислений (рис. 8) в виде подробного описания оптимального плана с указанием значения целевой функции (текущего рекорда) и объема ресурсов (размера переменных).
Полученный программный продукт можно использовать как в составе оптимизационной надстройки Optimal Software Toolkit, интегрирующей его в среду MS Visual Studio, так и в виде самостоятельного оптимизационного инструмента для анализа и оптимизации исходных кодов, написанных на ANSI «Си».
Заключение
Модели оптимизации на основе экстремальных подходов к повышению качества программных продуктов, полученные в ходе реализации второго этапа работ по проекту РФФИ, являются дополнением к методам оптимизации работы с медленной памятью и позволяют охватить практически все возможные условия функционирования программных продуктов: системы с избытком оперативной памяти провоцируют разработчика на использование экстремальных методов оптимизации, экстенсивно расходующих память, в то время как в системах, функционирующих в условиях недостатка ресурсов быстрой памяти, более актуальными являются методы, в основе которых идея минимизации числа обращений к внешней медленной памяти. Результаты могут найти применение в прикладных отраслях как одно из средств автоматизации на этапе оптимизации программных продуктов. Полученная по результатам исследований платформа позволит развивать исследования в направлении расширения функциональности оптимизационного пакета с учетом различных условий функционирования приложений и специфики требований к качеству разрабатываемых продуктов.
Работа выполнена при финансовой поддержке РФФИ и Минобрнауки Республики Северная Осетия – Алания в рамках научного проекта № 17-41-150812\18.
Литература
1. Томаев М.Х. Автоматизированные инструментальные средства оптимизации исходных кодов больших программных систем // ИТпортал. 2017. № 4. URL: http://itportal.ru/science/tech/
avtomatizirovannye-instrumentalnye-/ (дата обращения: 12.02.2018).
2. Касьянов В.Н. Практический подход к оптимизации программ. Н.: Препр. ВЦ СО АН СССР, 1978. № 135. 43 с.
3. Касьянов В.Н. Введение в теорию оптимизации программ. Н., 1985. 259 с.
4. Касьянов В.Н. Смешанные вычисления и оптимизация программ // Кибернетика. 1980. № 2.
С. 51–54.
5. Гроппен В.О. Принципы оптимизации программного обеспечения ЭВМ. Ростов-н/Д: Изд-во Ростов. ун-та, 1993. 164 с.
6. Гроппен В.О., Томаев М.Х. Модели, алгоритмы и средства программной поддержки проектирования оптимальных программных продуктов // Автоматика и телемеханика. 2000. № 11. С. 175–183.
7. Томаев М.Х. Технологии глобальной оптимизации пользовательских программных кодов. Автоматизация и управление в технических системах. 2015. № 3. С. 16–30. URL: auts.esrae.ru/15-277 (дата обращения: 12.02.2018); DOI: 10.12731/2306-1561-2015-3-2.
8. Касьянов В.Н. Эквивалентные преобразования линейных участков программ // Трансляция и преобразования программ. Н., 1984. С. 56–61.
9. Касьянов В.Н. Анализ структур программ // Кибернетика. 1980. № 1. С. 48–61.
10. Касьянов В.Н. Разгрузка участков повторяемости. Н.: Препр. ВЦ СО АН СССР, 1979. № 178. 26 с.
11. Дзелинская А.А. Чистка циклов в крупноблочных схемах // Языки и системы программирования. Н., 1981. С. 64–74.
12. Родзин С.И., Родзина О.Н. Поиск оптимальных решений комбинаторных задач: теория, эволюционные алгоритмы и их приложения для проблемно-ориентированных информационных систем // Информатика, вычислительная техника и инженерное образование. 2014. № 4. С. 18–33.

Комментарии