В настоящее время наблюдается экспоненциальный рост потребности в информации, которая, как правило, имеет слабоструктурированный характер (достаточно вспомнить текстовые информационные ресурсы Интернета). В этой связи можно выделить несколько важных проблем [1].

Во-первых, большое количество источников поиска информационных объектов (документов). При этом происходит постоянное пополнение информационных источников, хранилища которых зачастую пересекаются.

Во-вторых, сужение области поиска не только источников, но и самих объектов. Результаты запроса в общем случае – это перечисление источников, отсортированных, как правило, по морфологической и синтаксической близости документа к запросу. Возможность отбора документов, семантически близких указанному из всех найденных, существует, однако пользователю приходится просматривать в этом случае сотни объектов. То есть речь должна идти о действительно семантическом поиске документов.

В-третьих, поиск нужной информации становится все более сложным, трудоемким и неэффективным технологическим процессом. Пользователь, переходя от списка к списку документов, обязан уточнять критерии поиска и доводить свой запрос до некоторого оптимального набора слов, по которому он часто получает во многом знакомый ему перечень документов. Процесс поиска зацикливается, а время поиска значительно возрастает.

В статье предложен метод адаптивной кластеризации текстовых документов – результатов работы поисковой системы. Реализация метода предполагает, что для настройки параметров кластеризации должна использоваться информация, полученная не только от пользователя, но и в результате поиска документов. Идея заключается в использовании модифицированного нечеткого алгоритма кластеризации Гюстафсона–Кесселя. Для решения задачи определения количества кластеров при инициализации алгоритма предлагается использовать самоорганизующиеся карты Кохонена с динамически изменяемыми размерами. Приведены описание используемых алгоритмов и положительные результаты апробации метода на модельной задаче об ирисах Фишера. Показано, что на основе предложенного решения может быть построен список рубрик, объединяющих семантически связанные источники информации.

Теоретическое обоснование

С точки зрения пользователя система должна обладать хорошим соотношением таких, в некотором смысле противоположных, показателей, как полнота и точность поиска, а также выполнять новый поиск на основе полученных ранее результатов. Найденные и рубрицированные документы в большинстве случаев могут пересекаться по рубрикам, но у пользователя должен быть выбор между четкой и нечеткой рубрикацией. Кроме того, от пользователя, как от инициатора поиска, могла бы быть получена некоторая информация, необходимая для настройки параметров системы, но ее объем не должен превосходить разумных пределов.

С точки зрения реализации система должна использовать информацию и от пользователя, и полученную в результате поиска документов. В частности, по запросу пользователя определенным образом строится список найденных документов и, используя обработанный определенным образом запрос, вычисляется матрица весов документов – tf × idf [2]. На основе этой информации необходимо получить список рубрик и распределение документов по ним.

Для решения этой задачи предлагается выполнять нечеткую кластеризацию векторов документов матрицы весов. Проблема в динамически изменяющемся количестве компонент этих векторов в зависимости от видоизменения запроса. Также нужно учитывать и возможность классификации из-за возможного появления новых источников информации.

Методов кластеризации документов достаточно много, однако универсального нет. Каждый из них хорош (или даже оптимален) при выполнении ряда условий, но имеются и недостатки.

Метод SuffixTreeClustering [3] предполагает повторную обработку текстов документов. LSA/LSI [4] выполняет огромное количество вычислений и в результате своей работы выдает непересекающиеся кластеры. Для метода ConceptIndexing [5] необходимо наличие обучаемого варианта, задание количества кластеров. В SingleLink, CompleteLink, GroupAverage [6] полученные кластеры также не пересекаются. Главным параметром K-means и Fuzzy-C-Means [6] является задание количества кластеров. Для карт Кохонена SOM [6] основной недостаток, как правило, – это длительный процесс обучения.

Постановка задачи

Пусть документ d представляется набором терминов , которые влияют на отнесение документа к какой-либо рубрике, то есть документ – это вектор d = {t1, t2, …, tM}. Тогда мощность M пространства терминов T будет представлять размерность пространства документов. Координатами вектора документа, который предоставляется на обработку, будут величины значимости конкретного термина для этого документа. Если в некотором документе отсутствует термин tl, то l-я координата вектора принимается равной 0. В данной работе за основу взята мера tf*idf, при этом координаты документов в пространстве терминов преобразуются в матрицу весов документов.

Кластером C в пространстве терминов T назовем множество схожих, в смысле некоторой меры , векторов весов терминов документов. Тогда семантическую схожесть документов будет определять выбранная мера схожести r представляющих их векторов. Таким образом, необходимо провести кластеризацию множества документов . В итоге необходимо получить разбиение C= C1 È C2 È …È CK множества D на возможно пересекающиеся группы, где каждому документу будет приписана степень принадлежности каждому кластеру, определяющая вес значимости документа для каждого кластера-рубрики.

Важным вопросом является определение «качества» кластеризации – разбиение множества документов на «правильное» количество кластеров. На сегодняшний день не существует единого подхода для определения наилучшего количества кластеров. Известны лишь верхняя и нижняя оценки на количество кластеров K. В качестве ограничений на количество кластеров обычно берутся границы интервала , где N – количество документов.

Описание предлагаемого метода кластеризации

Для решения указанной задачи в различных источниках ([7], [8]) предлагается вычислять так называемые функционалы качества. Далее приведены некоторые из них и условия для нахождения оптимального количества кластеров:

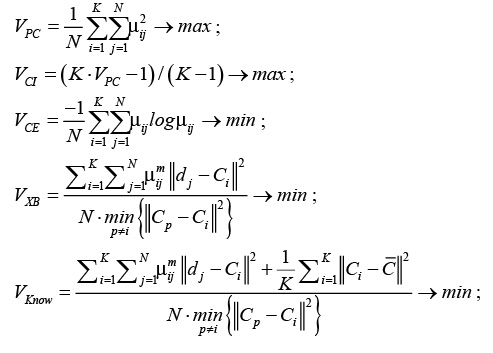
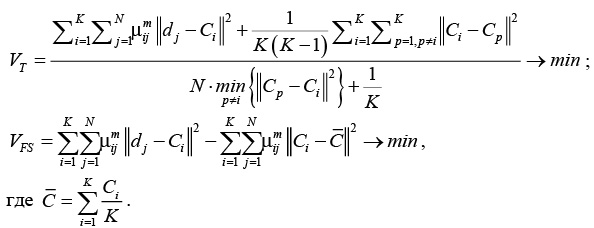
где .

Исходя из такой постановки задачи, для поиска количества кластеров и соответствующего разбиения можно следовать следующему алгоритму.

Задать Kmin, Kmax

p = Kmin

repeat

Провести кластеризацию C= C1 È C2 È …È Cp.

Вычислить индекс(-ы) для полученного варианта кластеризации:

if индекс(-ы) достиг(-ли) оптимального значения then

                 return

    else

                p = p + 1

    endif

untilp £ Kmax

Здесь на каждом шаге алгоритма необходимо запускать некоторый метод кластеризации и вычислять значения функционалов. При этом нужно следить за «скачками» этих функционалов или разработать некоторый алгоритм для вычисления оптимума того или иного функционала, что в указанной постановке весьма проблематично, так как сами функционалы содержат информацию о разбиении. Также нужно обращать внимание на варианты кластеризации, при которых произошли эти «скачки». На следующем этапе необходимо просматривать выделенные варианты кластеризации и выбрать наилучший. Очевидно, что вычислительная сложность такого подхода резко возрастает с увеличением объема входных данных. Также нужно отметить, что при изменении объема входных данных нужно заново запускать этот алгоритм, что также увеличивает временную сложность работы алгоритма.

Апробация вышеописанного алгоритма была проведена на тестовых данных, известных как ирисы Фишера. В качестве алгоритма кластеризации применялся классический алгоритм Гюстафсона–Кесселя, учитывающий формы кластеров. Количество кластеров изменялось от 2 до 7. Результат работы алгоритма приведен в таблице.

 

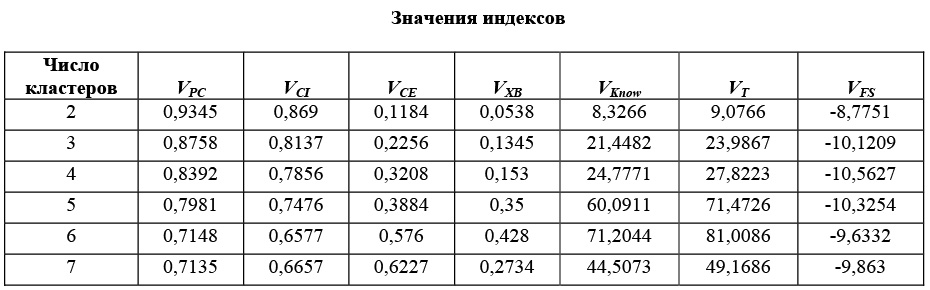
Видно, что с точки зрения оптимальности функционалов наилучшим можно считать вариант разбиения исходного множества на два кластера. В качестве подтверждения правильности оценки количества кластеров, указанной выше, можно отметить тот факт, что при выборе большего количества кластеров значения функционалов принципиально не отличаются от значений, полученных для последнего варианта кластеризации.

 

Одним из вариантов решения задачи определения количества кластеров может быть модифицированный алгоритм SOM [9].

1. Инициализация. Для исходных векторов семантических весов wj(0) выбираются случайные значения. Единственным требованием является различие векторов для разных значений j = 1, …, K, где K – общее количество нейронов в решетке. При этом рекомендуется сохранять малую амплитуду значений. Например, можно рандомизировать аргумент функции синуса. Веса нейронов рекомендуется нормализовать.

2. Подвыборка. Из входного пространства выбирается вектор d с определенной вероятностью. Размерность вектора равна M.

3. Поиск максимального подобия. Осуществляется поиск нейрона-победителя id(x, y) на шаге t, используя критерий минимума евклидова расстояния:

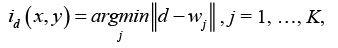
где (x, y) – координаты нейрона в решетке. На этом шаге необходимо учитывать проблему «мертвых» нейронов. Для ее решения использовались следующие положения. Учитывая тот факт, что после победы нейрон «отдыхает», необходимо «ограничить» его активность на следующем этапе обучения [10]. Для этого можно вести учет активности нейронов:

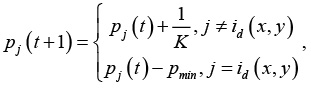
где pmin – минимальный «потенциал», разрешающий участие нейрона в конкурентной борьбе. На практике хороший результат дает pmin = 0.75. Кроме того, количество побед нейронов учитывается [9] при поиске нейрона-победителя, что позволяет задействовать часть нейронов из области пространства, где отсутствуют данные или их количество ничтожно мало:

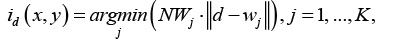
где NWj – количество «побед» нейрона j.

4. Коррекция. Корректируются векторы семантических весов всех активных нейронов, используя формулу

,

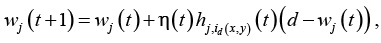где  – параметр скорости сходимости;  – функция окрестности нейрона-победителя id(x, y). Оба этих параметра динамически изменяются:

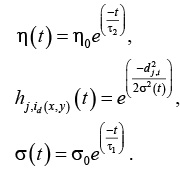
Здесь h0 – начальное значение скорости сходимости, рекомендуемое значение 0.1, при этом h(t) не должно быть менее 0.01; s(t) – ширина топологической окрестности нейрона, на начальном этапе s0 полагают равной радиусу решетки, что означает активность всех нейронов сети на начальном этапе обучения; 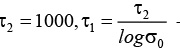 – временные параметры.

Продолжение. Возврат к шагу 2. Вычисления продолжаются до тех пор, пока в карте признаков не перестанут происходить заметные изменения.

Преимущество этого алгоритма заключается в том, что он самостоятельно может определить первоначальное распределение центров кластеров [9]. Процесс адаптации нейрона-победителя позволяет так настроить его веса, что он становится «ковариационным центром» найденного кластера.

На данном этапе открытым остается вопрос о размере решетки нейронов. В данном случае задача поиска количества кластеров преобразуется в задачу определения размера нейронной сети. Для ее решения была позаимствована идея иерархических методов кластеризации, где разбиение начинает строиться с единственного кластера, который в процессе кластеризации дробится на некоторое конечное число кластеров в соответствии с некоторым условием.

Примененный алгоритм определения размеров карты Кохонена предусматривает, что для каждого кластера вычисляется величина

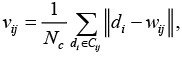
где Cij – множество векторов, отнесенных к j-му кластеру, Nc – количество документов в Cij.

В данном случае весь процесс обучения необходим для определения количества кластеров, то есть возможно изменение карты. Для определения ее новых размеров ищется нейрон w*, для которого vij максимален:

.

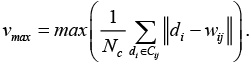Чтобы не нарушать «обученность» нейронов, вся карта не перестраивается, добавляются только строка и столбец нейронов между нейроном w* и нейроном, для которого расстояние, в смысле выбранной метрики, наибольшее. Далее инициализируются веса добавленных нейронов, для чего использовался самый простой способ – вычисление средневзвешенного веса нейронов из топологической окрестности.

В качестве критерия остановки изменения размеров карты предложен следующий критерий:

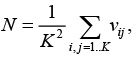
где N < 0.55vpmax, vpmax – величина, определенная на предыдущем шаге конкретизации карты.

Для дальнейших исследований необходимо в условие остановки увеличения размера сети включить семантическую «обособленность» кластеров.

На последнем этапе формируются кластеры при помощи алгоритма Гюстафсона–Кесселя.

Таким образом, в статье описан метод адаптивной кластеризации текстовых документов и показана его применимость к решению задачи построения списка рубрик, объединяющих семантически связанные источники информации.

Авторы предполагают, что предложенный метод будет использован в разработке модуля классификации и идентификации связей текстовых документов и мультимедийных объектов интеллектуальной системы информационной поддержки инноваций в науке и образовании [2]. В результате для кластеров семантически связанных данных должны быть выполнены оценка качества классификации, отбор объектов с высокой степенью релевантности и интерпретация результатов. Эти модули завершают генерацию решений, имеющих инновационный потенциал, которая осуществляется в заданном тематическом сегменте или по заданному объекту (промышленному изделию, технологии, продукту).

В настоящее время готовится программная реализация описанного в статье метода, предназначенная для включения в программный продукт GeneticAlgorithmFramework (GAF), представленном в [10].

Литература

1. Маннинг К.Д., Рагхаван П., Щютце Х. Введение в информационный поиск; [пер. с англ.].
М. :Вильямс, 2011. 528 с.

2. Палюх Б.В., Иванов В.К., Сотников А.Н. Архитектура интеллектуальной системы информационной поддержки инноваций в науке и образовании // Программные продукты и системы. 2013. № 4.
C. 197–202.

3. Zamir O.E. Clustering Web Documents: A Phrase-Based Method for Grouping Search Engine Results. Univ. of Washington, USA, 1999, pp. 65–117.

4. Deerwester S., Dumais S.T., Furnas G.W., Landauer T.K., Harshman R. Indexing by Latent Semantic Analysis. Journ. of the American Society for Information Science, 1999, vol. 41, pp. 391–407.

5. 5an E.-H. (Sam), and Kapyris G. Proc. 4th Europ. Conf. on Principles and Practice of Knowledge Discovery in Databases (PKDD), 2000, pp. 424–431.

6. Барсегян, А.А., Куприянов М.С., Холод И.И., Тесс М.Д., Елизаров С.И. Анализ данных и процессов: учеб. пособие. 3-е изд. СПб.: БХВ-Петербург, 2009. 512 с.

7. Duo С. et al. An Adaptive Cluster Validity Index for the Fuzzy CMeans. Intern. Journ. of Comp. Sc. and Network Security, 2007, vol. 7 (2), pp. 146–156.

8. Tang Y., Sun F., Sun Z. Improved Validation Index for Fuzzy Clustering, in American Control Conf., 2005, pp. 1120–1125.

9. Виноградов Г.П., Мальков А.А. Эволюционные методы кластеризации, использующие нечеткие отношения и субъективные оценки: сб. тр. Междунар. науч.-технич. конф. AIS’08, CAD-2008. М.: Физматлит. Т. 1. С. 7–15.

10. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы; [пер. с польск. И.Д. Рудинского]. М.: Горячая линия–Телеком, 2013. 384 c.

11. Иванов В.К., Мескин П.И. Реализация генетического алгоритма для эффективного документального тематического поиска // Программные продукты и системы. 2014. № 4. С. 118–126; DOI:10.15827/0236-235X.108.118-126.