Современные подходы к решению задачи стабилизации перевернутого маятника

Перевернутый маятник является классической задачей в динамике и теории управления и широко используется в качестве эталона для тестирования алгоритмов управления (PID-controllers, нейронных сетей, нечеткого управления, генетических алгоритмов и т.д.).

Существует множество методов, позволяющих осуществлять контроль над перевернутым маятником, такие как классические методы управления и методы, основанные на применении теории машинного обучения. Системы ракетного управления, робототехника, управление строительными кранами являются основными областями применения данных методов, однако наибольшее применение они нахо-
дят в стабилизации подъемных кранов в верфи. При перемещении морских контейнеров вперед-назад краны работают так, что отсутствуют какие-либо виды колебаний или раскачиваний. Кран всегда остается в хорошо зафиксированном положении, даже когда по какой-либо причине происходит экстренная остановка.

Система перевернутого маятника имеет два вида равновесий, одно из которых является устойчивым, а другое – неустойчивым. Устойчивое равновесие относится к состоянию, аналогичному подвешенному вниз маятнику. В отсутствие какой-либо удерживающей силы данная система будет возвращаться к исходному состоянию. Устойчивое равновесие не требует контроля и поэтому является более простой задачей с точки зрения управления. Неустойчивое равновесие соответствует состоянию,
в котором маятник располагается строго вверху, требуя некоторой силы для сохранения данного положения. Задача системы управления состоит в удержании перевернутого маятника в вертикальном положении за счет смещения тележки.

Система обратного маятника (закрепленного, к примеру, на валу двигателя) может быть применена
в робототехнике при движении роботов-гуманоидов. С помощью двигателей изменяется угол положения составных частей робота, что позволяет сохранить точку его равновесия и не дает роботу упасть. Также данная система применяется для стабилизации положения ракетных установок. Перевернутый маятник был центральным компонентом в разработке ранних сейсмографов. Доступное применение – балансировка, например в акробатике.

Существующие решения

Достижение устойчивости перевернутого маятника стало вызовом для исследователей. Существуют различные вариации перевернутого маятника, например, многозвенные маятники (маятник Капицы, маятник Фуруты), маятник с неподвижной точкой опоры, маятник с колеблющимся основанием и, как
в рассматриваемой задаче, маятник на тележке. Существует вариант двухколесной балансировки перевернутого маятника (сигвей) – позволяет вращаться на месте, предлагая большую маневренность. Еще одна разновидность – балансировка на одной точке. Волчок, одноколесный велосипед (юнисайкл), перевернутый маятник с закрепленной наверху сферой – все это балансировка на одной точке. Как было определено выше, маятники могут быть воссозданы при наличии вертикальной осциллирующей базы.

Уравнения движения и использование различного рода регуляторов для решения задачи
перевернутого маятника

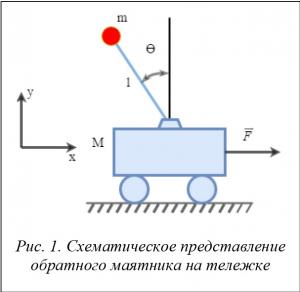
В физическом смысле перевернутый маятник на тележке состоит из массы m на вершине стержня длины l, вращающегося на горизонтально подвижной основе (тележке). Тележка ограничена линейным движением, и ее перемещение зависит от сил, приводящих в движение или препятствующих ему (рис. 1).

С математической точки зрения стабилизация перевернутого маятника может быть сведена к трем основным шагам.

Если угол наклона q смещен вправо, тележка должна ускоряться вправо и наоборот.
Положение тележки х относительно ее центра стабилизируется путем моделирования нулевого угла (погрешность угла, которую система управления пытается привести к нулю) положением тележки, то есть нулевой угол = q + kx, где k мало. Это заставляет стержень слегка отклоняться относительно центра тележки и стабилизировать положение там, где угол отклонения расположен точно по вертикали. Любые изменения или наклон тележки могут вызвать нестабильность системы, что выражается в ее постоянном перемещении. Добавочные перемещения позволяют контролировать положение системы.
Обычный маятник с учетом движущейся точки поворота (например груз, перемещаемый краном) обладает пиковым откликом при частоте колебаний маятника 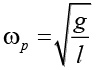. Для предотвращения бесконтрольных колебаний частотный спектр движущегося основания должен быть в пределах wp. Перевернутый маятник требует тех же пределов частоты, чтобы достичь стабильного положения.

Если перемещение тележки будет положительным, то внезапное движение вправо повлечет за собой движение влево, за которым последует движение вправо, чтобы стабилизировать положение маятника.

Уравнения движения перевернутых маятников зависят от того, какие ограничения положены на движение маятника. Перевернутые маятники могут иметь различную конфигурацию, что приводит к ряду уравнений движения, описывающих поведение маятника.

Данные уравнения могут быть получены с помощью уравнений Лагранжа. Пусть q(t) – угол между маятником длины l по отношению к вертикальной оси, а действующие силы – это сила тяжести и внешняя сила F в х-направлении. x(t) – положение тележки. Лагранжиан L = T – V системы

где v1 – скорость тележки, v2 – скорость точечной массы m. v1 и v2 могут быть выражены через x и с помощью записи скорости как первой производной положения тележки x:

Упростив выражение для v2, получим

Теперь лагранжиан задается следующим образом:

и уравнения движения имеют вид

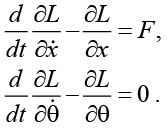
Подстановка L в эти уравнения и их упрощение ведут к уравнениям, описывающим движение перевернутого маятника:

Данные уравнения являются нелинейными, но, поскольку цель системы управления – держать маятник в вертикальном положении, уравнения могут быть линеаризованы по q ~ 0.

В некоторых случаях использовать второй закон Ньютона вместо уравнений Лагранжа удобнее, поскольку уравнения Ньютона дают силу реакции в месте соединения маятника и тележки. Эти уравнения дают два уравнения: одно для х-направления и другое для y-направления. Уравнения движения тележки представим как

В данных уравнениях и являются силами реакции в месте соединения маятника и тележки,
FN – сила реакции, приложенная к тележке. Второе уравнение зависит только от силы реакции, приложенной к тележке, следовательно, уравнение может использоваться для нахождения данной силы. Первое уравнение может быть использовано для нахождения горизонтальной силы реакции. Для дополнения уравнения движения должно быть найдено ускорение точечной массы (масса, сосредоточенная в материальной точке), прикрепленной к маятнику. Положение данной точечной массы может быть выведено
в инерциальных координатах как

Взяв вторую производную от данного уравнения, получим вектор ускорения в инерциальной системе отсчета. Далее, используя второй закон Ньютона, эти два уравнения могут быть записаны
в x-направлении и y-направлении. Отметим, что силы реакции положительны по отношению к маятнику и отрицательны по отношению к тележке. Это следствие третьего закона Ньютона:

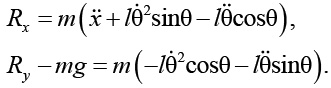
Первое уравнение дает еще один способ нахождения горизонтальной силы реакции в случае, когда приложенная сила F неизвестна. Второе уравнение может быть использовано для нахождения вертикальной силы реакции. Первое уравнение движения получено путем замены .

При детальном рассмотрении можно заметить, что получился результат, идентичный полученному методом Лагранжа.

Компоненты инерциальной системы можно записать как , это означает, что стержень может осуществлять перенос нагрузки только вдоль своей оси. Данное утверждение порождает еще одно уравнение, которое может быть использовано для нахождения силы реакции самого стержня:

После всех подстановок и упрощений будет получено уравнение

которое идентично результирующему уравнению, полученному в результате применения уравнений Лагранжа.

В свою очередь, существует подход к решению задачи, использующий различного рода регуляторы. Простой регулятор, качающий маятник из стороны в сторону, может быть рассчитан на основании физических законов, заставляющих его занять устойчивое положение. Постоянная сила может быть приложена к тележке в соответствии с направлением угловой скорости маятника, так что, маятник будет колебаться до тех пор, пока не достигнет положения в непосредственной близости от нулевого отклонения (исконно вертикальное положение). Уравновешивающий регулятор является стабилизирующим линейным регулятором, который может быть представлен как PD PID-регуляторами, а также линейно-квадратичным регулятором (LQR), или же может быть спроектирован с помощью метода размещения полюсов (метод Аккермана [1]).

Алгоритм, использующий концепцию LQR, в сравнении с традиционным методом размещения полюсов автоматически выбирает замкнутый контур в соответствии с весами, которые, в свою очередь, зависят от ограничений системы. LQR – в теории управления один из видов оптимальных регуляторов,
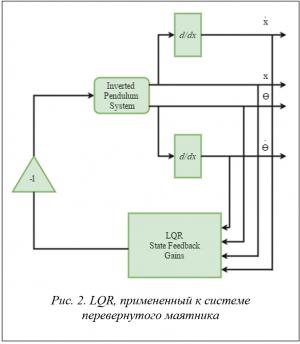
использующий квадратичный функционал качества. Гибкость – единственная причина его популярности. Система перевернутого маятника имеет множество физических ограничений, следовательно, есть смысл использовать данный алгоритм. Выбор индексов квадратичного представления зависит от физических ограничений и желаемой производительности замкнутого контура системы управления. Любое состояние обратной связи может быть обобщено для линейных стационарных систем (рис. 2):

Если все n состояний доступны для обратной связи и все состояния полностью контролируемы, то существует обратная связь, представленная матрицей коэффициентов обратной связи K. Выбор K зависит от желаемых положений стержня, где пользователь намеревается управлять положением стержня так, чтобы было достигнуто желаемое качество управления.

Для реализации LQR можно отметить следующее.

Все весовые матрицы симметричны по своей природе.
Погрешность взвешенной матрицы Q неотрицательна, чтобы квадрат ошибки оставался положительным. Из-за квадратичной природы PI-регулятора большее внимание уделяется весомым ошибкам, нежели малым. Обычно она выбирается как диагональная матрица.
Взвешенная матрица управления R всегда положительно определена.

PID-регуляторы очень популярны благодаря простоте использования. Данные контроллеры также несложно реализовать, используя какие-либо электронные компоненты. Существует несколько вариантов настройки PID-регуляторов, например, метод Циглера–Николса [2], метод реле для нелинейных систем и другие. В данной системе используется вариант настройки с использованием метода размещения полюсов. Он включает в себя случай, когда две или более динамические системы связаны таким образом, что каждая система воздействует на другую и динамика сопряжена. Самым главным преимуществом обратной связи является тот факт, что она делает управление нечувствительным к внешним помехам и изменениям параметров системы.

Управляющий сигнал u полностью основан на сгенерированной ошибке e. Входная команда r в литературе по теории управления называется установкой весов.

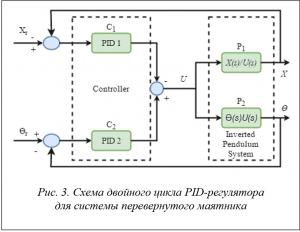
LQR-регулятор испускает нежелательные незатухающие колебания при ответной реакции тележки, что может быть предотвращено с помощью двойного цикла для PID-регулятора. Схема такого регулятора для перевернутого маятника представлена на рисунке 3.

LQR, как и PID, был успешным в обеспечении устойчивости системы при заданных входных параметрах. PID-регулятор с двойным циклом обеспечивает хорошую переносимость относительно различного рода многоканальных усилений на выходе. Из-за нелинейного поведения тележки существует отклонение от идеального поведения, что приводит к нежелательным колебаниям преимущественно в методах управления с обратной связью. Решение с LQR, полученное после выбора весов, хорошо тем, что автоматически заботится о физических ограничениях. Чтобы избежать нежелательных колебаний, применяется алгоритм, использующий PID-регулятор с двойным циклом. Данный подход приводит к упрочнению конструкции, что значительно сокращает колебания тележки.

OpenAI Gym. Сравнительная характеристика алгоритмов

Поставленная задача будет решаться при помощи платформы для разработки и сравнения алгоритмов обучения OpenAI Gym. Используемый язык для реализации – Python (v. 3). OpenAI Gym – это бесплатный инструмент для разработки и тренировки AI ботов с помощью игр и алгоритмических испытаний. Инструмент предназначен для использования вместе с обучением с подкреплением (Reinforcement Learning).

В OpenAI обучение с подкреплением – важный способ машинного обучения, который позволит в значительной степени усовершенствовать искусственный интеллект [3]. В процессе обучения таким методом испытуемая система (агент) обучается, взаимодействуя с некоторой средой. В отличие от традиционного обучения с учителем откликом на принятые решения искусственного интеллекта являются сигналы подкрепления, при этом некоторые правила подкрепления формируются динамически и трудны для понимания человеком, то есть базируются на одновременной активности формальных нейронов. OpenAI Gym состоит из набора сред [4], включая имитацию роботов и компьютерных игр Atari, а также сайт для сравнения и воспроизведения результатов. Откликом среды на принятые решения являются сигналы подкрепления, поэтому такое обучение является частным случаем обучения с учителем, но в данном случае учитель – это среда.

В статье представлены следующие алгоритмы [5]:

алгоритм случайного поиска (Random Search Algorithm);
алгоритм поиска с восхождением к вершине (Hill Climbing);
политика градиентов (Policy Gradient);
алгоритм обучения с подкреплением (Q-learning).

В моделируемой среде маятника в OpenAI Gym (рис. 4) существуют наблюдения, которые независимо от состояния системы предоставляют следующие данные: угол отклонения стержня и координаты положения тележки. Используя данные наблюдения, агенту нужно решиться на одно из возможных действий – двигать тележку влево или вправо.

Для сопоставления наблюдения и нужного действия используется линейная комбинация. Определим вектор весов, каждый вес соответствует одному из наблюдений. Объявим их в пределах [-1,1]:

parameters = np.random.rand(4) * 2 -1.

Каждый вес умножается на соответствующее значение, полученное в результате наблюдения, затем выполняется суммирование. Данная операция эквивалентна умножению матриц (или двух векторов). Если конечный результат меньше нуля, тележка двигается влево, иначе – вправо.

Action = 0 if np.matmul(parameters,
observation) < 0 else 1.

Для устойчивого положения маятника следует внести некоторые изменения.

Прежде всего необходима какая-либо концепция, чтобы расценивать полученный результат. Для каждого момента времени, когда маятник находится в равновесии, получаем +1 к награде. Далее, чтобы оценить, насколько хорош набор весов, можно запускать данный эпизод до тех пор, пока маятник не упадет, при этом наблюдая, что получится в итоге.

Def run_episode(env, parameters):

observation = env.reset()

totalreward = 0

for _ in xrange(200):

action = 0

if np.matmul(parameters,observation)<0 else 1

observation, reward, done, info = env.step(action)

totalreward += reward

if done:

break

return totalreward

Базовая модель готова, перейдем к рассмотрению алгоритма случайного поиска.

Случайный поиск – группа методов численной оптимизации, которые не требуют вычисления градиента для решения задач оптимизации.

Основная идея данного алгоритма заключается в том, что пробуются случайные веса и выбирается наилучший. В силу простоты системы перевернутого маятника данный алгоритм работает довольно быстро.

Bestparams = None

bestreward = 0

for _ in xrange(10000):

parameters = np.random.rand(4) * 2 – 1

reward = run_episode(env,parameters)

if reward > bestreward:

bestreward = reward

bestparams = parameters

if reward == 200:

break

Алгоритм поиска с восхождением к вершине представляет собой обычный цикл, в котором постоянно происходит перемещение в направлении роста некоторого значения, то есть подъем. Работа этого алгоритма заканчивается после достижения пика, в котором ни одно из соседних состояний не имеет более высокого значения.

Для начала выбираются случайные веса. С каждым эпизодом к этим значениям добавляется шум и, если поведение агента улучшается, новые веса сохраняются.

Noise_scaling = 0.1

parameters = np.random.rand(4) * 2 – 1

bestreward = 0

for _ in xrange(10000):

newparams = parameters + (np.random.rand(4) * 2 – 1)*noise_scaling

reward = 0

for _ in xrange(episodes_per_update):

run = run_episode(env,newparams)

reward += run

if reward > bestreward:

bestreward = reward

parameters = newparams

if reward == 200:

break

Основная идея алгоритма заключается в постепенном увеличении весов, а не в скачкообразном
в надежде найти какое-либо сочетание, которое работает. Если значение шума достаточно высокое по сравнению с текущим весом, этот алгоритм по существу является таким же, как и алгоритм случайного поиска.

Для воспроизведения алгоритма, использующего градиенты политик, нужно придерживаться политики постепенных изменений. Вместо одной линейной комбинации будут две: по одной на каждое возможное действие. При передаче этих двух значений через функцию активации (softmax function) появляется возможность выполнить соответствующие действия относительно полученного набора наблюдений.

Представим версию оптимизатора, который позволяет постепенно обновлять политики:

def policy_gradient():

params = tf.get_variable(“policy_parameters”,[4,2])

state = tf.placeholder(“float”,[None,4])

actions = tf.placeholder(“float”,[None,2])

linear = tf.matmul(state,params)

probabilities = tf.nn.softmax(linear)

good_probabilities = tf.reduce_sum

(tf.mul(probabilities,actions),reduction_indices=[1])

# maximize the log probability

log_probabilities = tf.log(good_probabilities)

loss = -tf.reduce_sum(log_probabilities)

optimizer = tf.train.AdamOptimizer(0.01).minimize(loss)

Если бы точно знать идеальные перемещения тележки в каждом состоянии, можно было бы просто продолжительно применять обучение с учителем и задача была бы решена. Но правильные перемещения неизвестны.

Необходимо определить лучшее действие для каждого состояния, поэтому для начала нужна база,
с которой можно сравнивать результат. В данном примере используем один скрытый слой нейронной сети:

def value_gradient():

# sess.run(calculated) to calculate value of state

state = tf.placeholder(“float”,[None,4])

w1 = tf.get_variable(“w1”,[4,10])

b1 = tf.get_variable(“b1”,[10])

h1 = tf.nn.relu(tf.matmul(state,w1) + b1)

w2 = tf.get_variable(“w2”,[10,1])

b2 = tf.get_variable(“b2”,[1])

calculated = tf.matmul(h1,w2) + b2

# sess.run(optimizer) to update the value of a state

newvals = tf.placeholder(“float”,[None,1])

diffs = calculated – newvals

loss = tf.nn.l2_loss(diffs)

optimizer = tf.train.AdamOptimizer(0.1).minimize(loss)

Чтобы натренировать данную сеть, нужно запустить несколько эпизодов для сбора данных. Это похоже на цикл в алгоритме случайного поиска или в алгоритме поиска с восхождением к вершине, за исключением того, что желательно на каждом шаге делать записи об изменениях: какое действие из какого состояния выбрано и какая награда за это получена.

# tensorflow operations to compute probabilities for each action,

# given a state

pl_probabilities, pl_state = policy_gradient()

observation = env.reset()

actions = []

transitions = []

for _ in xrange(200):

# calculate policy

obs_vector = np.expand_dims(observation, axis=0)

probs = sess.run(pl_probabilities,feed_dict={pl_state:

obs_vector})

action = 0 if random.uniform(0,1) < probs[0][0] else 1

# record the transition

states.append(observation)

actionblank = np.zeros(2)

actionblank[action] = 1

actions.append(actionblank)

# take the action in the environment

old_observation = observation

observation, reward, done, info = env.step(action)

transitions.append((old_observation, action, reward))

totalreward += reward

if done:

break

На следующем шаге нужно учесть награду от каждого изменения и обновить нейронную сеть, чтобы отобразить внесенные изменения. Важно не конкретное действие, взятое от каждого состояния, а среднее значение награды для состояния по всем действиям.

Vl_calculated, vl_state, vl_newvals, vl_optimizer = value_gradient()

update_vals = []

for index, trans in enumerate(transitions):

obs, action, reward = trans

# calculate discounted monte-carlo return

future_reward = 0

future_transitions = len(transitions) – index

decrease = 1

for index2 in xrange(future_transitions):

future_reward += transitions[(index2) + index][2] * decrease

decrease = decrease * 0.97

update_vals.append(future_reward)

update_vals_vector = np.expand_dims(update_vals, axis=1)

sess.run(vl_optimizer, feed_dict = {

vl_state: states, vl_newvals: update_vals_vector })

Понижение существенно уменьшает влияние награды, которая будет получена через несколько циклов алгоритма. Это приводит к отклонениям, которые могут уменьшить значение дисперсии, особенно
в случае удачного эпизода, который длился 100 шагов по времени, в то время как обычный эпизод длился 30.

Обновление политики может производиться в том числе и при помощи ранее полученных при различных состояниях значений. Алгоритм выбирает действия, награда за которые больше средней награды по всем возможным действиям из данного состояния. Ошибка между текущим и средним значением называется преимуществом. Как оказалось, можно просто подключить преимущество как данные и обновить политику.

for index, trans in enumerate(transitions):

obs, action, reward = trans

# [not shown: the value function update from above]

obs_vector = np.expand_dims(obs, axis=0)

currentval = sess.run(vl_calculated,feed_dict={vl_state:

obs_vector})[0][0]

advantages.append(future_reward – currentval)

advantages_vector = np.expand_dims(advantages, axis=1)

sess.run(pl_optimizer, feed_dict={pl_state: states, pl_advantages:

advantages_vector, pl_actions: actions})

Для этого необходимо внести незначительные изменения в алгоритм: добавить коэффициент масштабирования.

Был разработан алгоритм обучения с подкреплением (Q-learning). Q-learning – это метод, применяемый в искусственном интеллекте при агентном подходе. На основе получаемого от среды вознаграждения агент формирует функцию полезности Q, что впоследствии дает ему возможность уже не случайно выбирать стратегию поведения, а учитывать опыт предыдущего взаимодействия со средой.

Агент располагает некоторым множеством действий. Действия агента влияют на среду, агент в состоянии определить, в каком состоянии он находится в данный момент, и получает то или иное вознаграждение от среды за свои действия. Задачей агента является нахождение наилучшей стратегии.

Формально простейшая модель обучения с подкреплением состоит из множеств состояний окружения S, действий A, вещественнозначных скалярных выигрышей [6].

В Q-learning определяем функцию Q(s,a), обозначающую будущую награду, когда мы выполняем действие a (action) в состоянии s (state) [7]:

Q(st, at) = max Rt+1.

Если для выбора оптимальной стратегии используется функция полезности Q, то оптимальные действия всегда можно выбрать как действия, максимизирующие полезность:

p(s) = argmaxa Q(s,a),

где p представляет собой правило, по которому выбирается действие в каждом состоянии.

Функция полезности состояния s и действия a с точки зрения следующего состояния s¢ имеет вид:

Q(s,a) = r + gmaxa¢ Q(s¢,a¢) (уравнение Беллмана),

где r – будущая награда в предыдущем состоянии.

Главная идея алгоритма заключается в том, что можно итеративно приближать Q-функцию, используя уравнение Беллмана. Представим псевдокод алгоритма:

initialize Q[num_states, num_actions] arbitrarily

observe initial state s

repeat

select and carry out an action a

observe reward r and new state s’

[s,a]= [s,a] + a(r + gmaxa, Q[s¢,a¢]– Q[s,a])

until terminated

где a – скорость обучения (0 < a < 1), g – ограничивающая константа.

Одно из преимуществ Q-learning заключается в том, что данный алгоритм позволяет сравнить ожидаемую полезность доступных действий, не формируя модель окружающей среды.

На основании представленных в таблице данных можно сравнить алгоритмы по времени обучения, скорости работы и используемой памяти.

Алгоритм градиента политик оказывается сравнительно медленным по отношению к алгоритмам случайного поиска и поиска с восхождением к вершине. Отчасти это потому, что сначала нужно обучить функцию, прежде чем агент сможет сделать какие-либо предположения о том, какие действия лучше.
В то время как улучшения в первых двух алгоритмах происходят сразу, градиентному алгоритму для начала нужно собрать некоторую статистику, чтобы понять, как улучшить ее обучение.

Однако это гарантирует, что обновления всегда создают некоторые улучшения. В средах с гораздо более многомерными пространствами состояний методы случайного поиска и поиска с восхождением к вершине будут гораздо менее эффективными, поскольку вероятность улучшения при произвольных параметрах крайне мала. Градиенты политик, в свою очередь, гарантируют агенту движение к наиболее благоприятным условиям.

Простые алгоритмы всегда лучше при решении простых задач. Для более сложных сред градиенты политик позволяют агенту производить более последовательные обновления и постепенно улучшаться. В то же время стоит обратить внимание на алгоритм обучения с подкреплением, который решает поставленную задачу быстрее по времени и за сравнительно небольшое количество эпизодов, но при этом позволяет решать более сложные задачи.

Заключение

Задача стабилизации объекта управления «обратный маятник» является актуальной и имеет достаточно широкие области применения. Алгоритмы стабилизации могут быть применены в робототехнике при движении роботов-гуманоидов (с помощью двигателей изменяется угол расположения составных частей робота, что позволяет сохранить его точку равновесия и не дает ему упасть). Кроме того, перевернутый маятник являлся центральным элементом в конструкции ранних сейсмографов из-за их природной нестабильности в результате реакции на любое нарушение.

OpenAI Gym предлагает открытую платформу, в которой доступно несколько сред, имитирующих различные варианты окружающей среды, в том числе есть возможность имитации роботов и компьютерных игр Atari, а также сайт для сравнения и воспроизведения результатов. Ответом среды на принятые решения являются сигналы подкрепления, поэтому такое обучение является частным случаем обучения с учителем, но в данном случае учитель – это среда. Обучение с подкреплением (Reinforcement learning) позволяет решать любую задачу, предполагающую создание последовательности решений.

При помощи данной технологии можно управлять двигателями робота таким образом, чтобы он бегал и прыгал, или же сформировать интеллектуальную программу по ценообразованию и управлению резервами. С помощью обучения с подкреплением машины научатся понимать естественный язык, что приведет к созданию роботов нового поколения, способных быстро обучаться.

Литература

Simple reinforcement learning methods to learn CartPole. 2016. URL: http://kvfrans.com/simple-algoritms-for-solving-cartpole/ (дата обращения: 05.04.2017).
Синтез последовательных управляющих алгоритмов с использованием формулы Аккермана в пространстве состояний // Фундаментальные исследования. 2014. № 11. Ч. 7. С. 1516–1520). URL: http://www.fundamental-research.ru/ru/article/view?id=35798 (дата обращения: 05.04.2017).
Настройка типовых регуляторов по методу Циглера–Никольса. 2014. URL: http://portal.tpu.ru:7777/SHARED/b/BURKINEYU/Studing/Tab3/06-labtau-2014.pdf (дата обращения: 05.04.2017).
OpenAI Universe. Открытая платформа для тренировки сильного ИИ. 2016. URL: https://geektimes.ru/post/283384/ (дата обращения: 05.04.2017).
Как Элон Маск обесценил секретные разработки Google. 2016. URL: http://www.dsnews.ua/future/kak-elon-mask-obestsenil-sekretnye-razrabotki-google-03052016232700 (дата обращения: 05.04.2017).
Обучение с подкреплением // Machine learning. 2008. URL: http://www.machinelearning.ru/wiki/index.php?title=Обучение_с_подкреплением (дата обращения: 05.04.2017).
Guest Post (Part 1): Demystifying Deep Reinforcement Learning (Q-Learning). 2015. URL: https://www.nervanasys.com/demystifying-deep-reinforcement-learning/ (дата обращения: 05.04.2017).

Литература

Комментарии