(Работа выполнена при финансовой поддержке гранта РФФИ № 17-07-00997)

На сегодняшний день наиболее эффективным направлением в эволюционном моделировании являются вероятностные алгоритмы, основанные на процессах живой природы. Сопоставляя известные закономерности окружающего мира с некоторыми сферами человеческой деятельности, мы можем получить эффективный инструмент для решения трансвычислительных задач.

Методы и алгоритмы для решения трансвычислительной задачи разрабатываются уже не один десяток лет. Актуальность работы связана с тем, что эта задача является NP-полной и разработать алгоритм, который позволит получать оптимальное и при этом точное решение за приемлемое время, очень
сложно [1, 2]. Появление суперкомпьютеров, имеющих мощные ресурсы для вычислений, а также повышенные требования к проектируемым устройствам являются главными причинами исследования и разработки новейших методов и алгоритмов для решения поставленной задачи.

Самоорганизующиеся системы можно описать с помощью роевого интеллекта. Системы роевого интеллекта являются многоагентными; каждый агент взаимодействует с остальными агентами и с окружающей средой. Сами агенты примитивны, но все вместе, при локальном взаимодействии, создают так называемый роевой интеллект. Примером в природе могут служить рой пчел, стая птиц, колония муравьев [1, 3, 4].

В статье рассматривается одна из основных трансвычислительных задач – задача размещения. Описывается гибридный алгоритм поиска решений для задачи размещения компонентов сверхбольших интегральных схем (СБИС). Разработанный алгоритм представляет собой композицию сразу трех алгоритмов: алгоритма на основе поведения колонии пчел, модифицированных генетического (ГА) и эволюционного (ЭА) алгоритмов.

Основу поведения пчелиного роя составляет самоорганизация, обеспечивающая достижение общих целей роя на основе низкоуровневого взаимодействия. Основная идея парадигмы пчелиной колонии заключается в использовании двухуровневой стратегии поиска [1, 3, 4]. На первом уровне с помощью пчел-разведчиков формируется множество перспективных областей, на втором уровне с помощью пчел-фуражиров осуществляется исследование окрестностей данных областей. Цель пчелиной колонии – найти источник, содержащий максимальное количество нектара. Также в статье представлен способ кодирования-декодирования найденных решений методами эволюционных вычислений.

Роевой алгоритм размещения

Задача размещения включает в себя описание расположения элементов относительно друг друга на плоскости с учетом заданных критериев. На их основе формируется целевая функция (ЦФ). Сформулируем задачу размещения. Есть множество элементов и множество позиций на коммутационном поле (КП) [1, 3, 4]. Нужно распределить элементы по позициям с учетом критериев так, чтобы ЦФ имела наиболее приближенное к оптимальному значение. Моделью представления цепи является звездный граф. Центром графа будет вершина, которая ближе всех расположена к геометрическому центру области, описывающей все вершины графа.

В предложенном алгоритме все решения являются точками (позициями) x_s в многомерном пространстве, а координаты позиции x_i – параметром функции F_s, которую необходимо оптимизировать. Все позиции сопоставляются с источниками нектара. Общий объем нектара, который содержится в источнике, можно определить координатами соответствующей позиции. Значение ЦФ в каждой точке будет равно количеству найденного нектара.

Основной идеей поведенческой модели самоорганизации колонии пчел является разработка методов и механизмов

– формирования роя агентов-разведчиков и роя агентов-фуражиров;

– поиска перспективных позиций разведчиками;

– выбора базовых позиций среди перспективных для исследования их окрестностей;

– передачи информации между разведчиками и фуражирами;

– выбора фуражирами базовых позиций;

– выбора фуражирами позиций в окрестности базовой позиций;

– общей структуры оптимизационного процесса [2].

Рассмотрим организацию поисковой процедуры на основе моделирования адаптивного поведения пчелиной колонии.

Ввод схемы и параметров алгоритма. Посадочные места под компоненты имеют фиксированные габариты в виде прямоугольников. Вначале вводятся параметры полей x и y, где x – количество посадочных мест по горизонтали, y – количество посадочных мест по вертикали, после чего инициализируется количество деталей, размещенных в этих ячейках. Количество посадочных мест должно быть меньше количества компонентов. Также формируется матрица связности. В нашем случае можно генерировать матрицу связности случайным образом (random) или выбрать корректировку в ручном режиме. В матрице связности определяется привязка компонентов к посадочным местам. Схема генерируется случайным образом, поскольку не стоит задача связать программу с какой-то конкретной схемой. Вводим данные для биоинспирированного алгоритма: количество итераций, число разведчиков и фуражиров (пчелы-сборщики) [5].

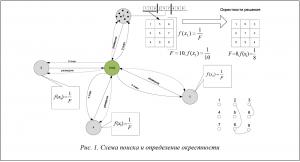
Разведчики формируют случайные решения R. Выдвигаясь из улья, они генерируют строку решений для всех ЦФ в поисковой области. Затем прилетают обратно в улей, чтобы сообщить пчелам-фуражирам о полученных решениях. Для данной задачи минимальное число связей элементов – это значение ЦФ. После этого в зависимости от значения ЦФ начинают действовать фуражиры. Полный процесс формирования показан на рисунке 1.

Опишем схему работы роевого алгоритма. Количество итераций определяется с помощью исходных данных. После выполнения последней итерации все наилучшие значения записываются. Затем производится поиск решений в окрестностях найденных точек. Пчелы-фуражиры, как только покинут улей, направляются на обследование окрестностей предположительных точек решений, производя при этом поиск наилучшего решения ЦФ в новых точках.

Формирование решений F в найденных окрестностях. После поиска в окрестностях формируются лучшие решения. Минимальное значение ЦФ будет главным критерием отбора найденных решений. Затем выводится лучшее решение. После проведения поиска лучшего решения ЦФ строится матрица смежности для найденных решений и осуществляется возврат к итерации по поиску решений. Количество решений зависит от количества итераций [5, 6].

Запись лучшего найденного результата за все пройденные итерации. После получения лучшего решения ЦФ результат записывается в матрицу связности и решение выводится на схему. Полученное решение отображается графически с помощью размещения компонентов (деталей в посадочных местах), то есть элементы, размещенные ранее, перераспределяются и устанавливаются на новые посадочные места, которые уже были размещены на коммутационном поле.

Схема гибридного поиска

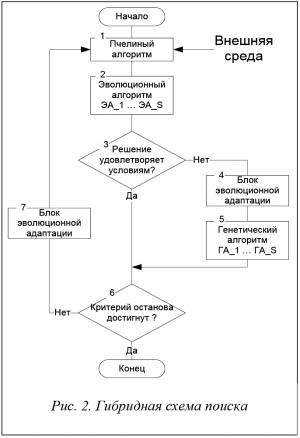
Во время разработки алгоритма использовался комбинированный подход, результатом которого является новый гибридный алгоритм, который вобрал в себя три использованных алгоритма, это гибридный алгоритм размещения элементов СБИС. Он представляет собой композицию сразу трех алгоритмов: алгоритма, основанного на поведении колонии пчел, ГА и ЭА. Основной идеей является разбиение процесса поиска на два этапа. Первый этап основан на пчелином алгоритме, который включает в себя нахождение областей с потенциально высоким значением ЦФ и строительство окрестности последующего поиска на основе полученных значений. На первой итерации множество решений генерируется автоматически. Второй этап включает в себя процесс нахождения множества решений для всех окрестностей. Окрестность – это совокупность альтернативных решений из заданной области. ЭА осуществляет поиск по каждой окрестности. В отличие от ГА данный подход работает только на основе оператора мутации, который требует меньше времени на выполнение. В конце работы ЭА производится проверка на выполнение всех условий. Если хотя бы одно решение, полученное во время работы ЭА, удовлетворяет условиям, данное решение записывается в буфер решений. Если получено несколько решений, перемещается только одно – лучшее решение. В противном случае для рассматриваемой окрестности инициализируется ГА с теми же стартовыми условиями, что и ЭА. Предложенный алгоритм имеет большую вычислительную сложность, но обеспечивает появление качественно новых оптимальных решений [6].

Укрупненная схема работы разработанного механизма поиска показана на рисунке 2.

Для начала работы ГА и ЭА генерируется начальная популяция решений. Существуют три известные стратегии создания начальной популяции: «одеяло», «дробовик», «фокусировка» [5]. Для описываемого алгоритма использована стратегия «фокусировка» для формирования начальной популяции решений, так как полученная на этапе работы пчелиного алгоритма окрестность является множеством решений для заданной области.

Кодирование решения

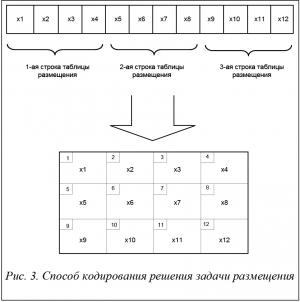
В представленном алгоритме все решения являются хромосомами, описываемыми линейной последовательностью генов. Хромосома соответствует определенному упорядочению вершин гиперграфа, описывающего схему проектируемого устройства. При этом размер хромосомы (то есть количество генов в ней) будет равно числу вершин в графе [2].

На рисунке 3 представлена структура хромосомы, используемая для перехода от хромосомы к размещению элементов на дискретном рабочем поле. Размер хромосомы 12, что равно числу элементов схемы, при этом размер дискретного рабочего поля задачи размещения – 4 на 3 ячейки. Хромосома разбивается на участки, формирующие в будущем наше дискретное рабочее поле. Значение гена представляет собой нумерацию элементов в схеме, которые размещаются в ячейках в соответствии с номером гена. Каждое новое решение является очередной перестановкой вершин. Представленный способ кодирования хромосомы является самым распространенным, но для выбранного критерия решения задачи в работе представлен новый, более эффективный подход к кодированию хромосомы, учитывающий реальные топологические параметры схемы. На рисунке 3 представлен способ кодирования хромосомы, являющийся очень простым в реализации, но при этом эффективным для метрических критериев решения задачи размещения.

Предлагаемый подход кодирования хромосом для поставленной задачи в следующем. Для каждого гена в хромосоме ставится в соответствие определенный статус:

– фиксированный элемент (позиция элемента, который кодируется текущим геном, является постоянной; в процессе выполнения генетических операторов ген не меняет своего значения, то есть положения в решетке);

– свободный элемент (элемент, который не инцидентен ни одной цепи, такие элементы размещаются в последнюю очередь);

– максимально-связный элемент (элемент с максимальной локальной степенью);

– элемент цепи критического пути (элемент, который принадлежит цепи, входящей в критический путь схемы).

Статусы генов позволят наиболее эффективно производить процесс декодирования. В процессе декодирования не участвуют неперемещаемые и свободные элементы. Все элементы критического пути размещаются максимально близко друг к другу (если позволяют параметры, критический путь можно выстроить в одну линию). Все последующие элементы располагаются так же, как и в представленном на рисунке 3 методе кодирования.

Декодирование решений

Самой значимой областью исследований является нахождение места и числа точек разрыва хромосомы для дальнейшего выполнения операторов скрещивания или мутации. Нужно учитывать, что большое количество разрывов может лишить нас лучших решений, а небольшое число чаще всего приводит к попаданию в локальный оптимум. Решение этой задачи является актуальной частью проводимых исследований [4, 7, 8].

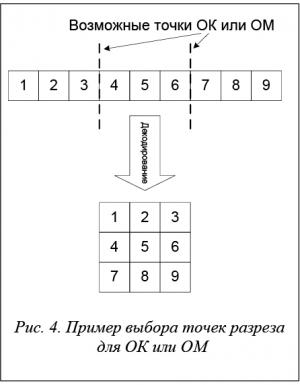
Рассмотрим оператор кроссинговера (ОК). Он представляет собой основу генетических операторов и формирует новые хромосомы (решения задачи) при помощи скрещивания двух хромосом родителей. Значение вероятности выживания потомков после применения классического ОК сильно уменьшается при увеличении размерности задачи, а следовательно, и количества генов в хромосоме. Для решения данной проблемы используется многоточечный ОК с классической схемой формирования точек кроссинговера. Предлагаемый подход заключается в разработке проблемно-ориенти-рованного ОК, который основывается на знаниях о решаемой проблеме, когда формируются точки скрещивания.

В данной статье решения задачи размещения с описанной методикой кодирования хромосом генерируются случайные точки разреза в местах (генах) перехода на новую строку решетки. Идентичным образом выбираются точки разреза при выполнении оператора мутации (ОМ).

На рисунке 4 представлен пример выбора точек разреза для ОК или ОМ.

Для хромосом большой размерности используются операторы с множеством точек разреза. Вероятность выживания хромосомы-потомка после выполнения модифицированного одноточечного проблемно-ориентированного ОК (ПООК) выражается с помощью формулы (L – длина хромосомы, N – число участков между точками скрещивания) [3]:

Экспериментальные исследования

Были проведены исследования по определению эффективности предложенного способа кодирования решений и выбора точек разреза для модифицированных генетических операторов.

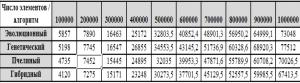
Проведена серия экспериментов для разного набора тестовых примеров, различающихся количеством элементов в схеме. Для каждого алгоритма на каждом тестовом примере было произведено 10 запусков
и на их основе определено среднее время работы алгоритма и среднее качество полученных решений. Усредненные результаты экспериментов отражены в таблице.

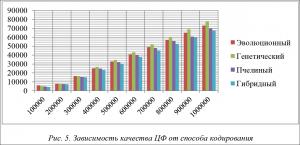
Зависимость качества ЦФ от способа кодирования

На рисунке 5 отображена зависимость качества значений ЦФ от используемого способа кодирования решений.

Заключение

На основе сравнительного анализа существующих подходов и методов для решения рассматриваемой задачи размещения использованы мультиагентные методы интеллектуальной оптимизации, базирующиеся на моделировании адаптивного поведения пчелиной колонии. В работе задача размещения представлена в виде гибридного алгоритма, включающего в себя роевой интеллект, ГА и ЭА.

Результаты исследований позволяют сделать вывод о том, что предложенный способ кодирования эффективнее классического подхода на 14–18 %. Использование предложенного подхода к кодированию в совокупности с гибридной схемой поиска позволяет эффективно управлять поиском и получать квазиоптимальные решения за полиномиальное время.

Литература

1. Лебедев Б.К., Лебедев О.Б. Методы размещения: монография. Таганрог: Изд-во ТТИ ЮФУ, 2012. C. 78–80.
2. Лебедев Б.К., Лебедев В.Б., Лебедев О.Б. Методы, модели и алгоритмы размещения: монография. Ростов н/Д: Изд-во ЮФУ, 2015. 150 с.
3. Кулиев Э.В., Лежебоков А.А., Кравченко Ю.А Роевой алгоритм поисковой оптимизации на основе моделирования поведения летучих мышей // Изв. ЮФУ: Технич. науки. 2016. № 7. С. 53–62.
4. Лебедев Б.К., Кулиев Э.В., Холопова Н.В. Генетический алгоритм разбиения с учетом принципов биогеографии. Информатика, вычислительная техника и инженерное образование. 2015. № 3. С. 1–9.
5. Лебедев В.Б., Лебедев О.Б. Роевой интеллект на основе интеграции моделей адаптивного поведения муравьиной и пчелиной колонии // Изв. ЮФУ: Технич. науки; Тематич. вып.: Интеллектуальные САПР. 2013. № 7. С. 41–47.
6. Lebedev B.K., Lebedev B.K., Kudryakova T.Y. Mechanisms of Adaptive Ant Colony Behavior in Placement Problem. Advances in Intelligent and Computing. Proc. of the I Intern. Sc. Conf. IITI’16. Springer, Czech Republic, 2016, vol. 1, pp. 443–451.
7. Кулиев Э.В., Лежебоков А.А., Дуккардт А.Н. Подход к исследованию окрестностей в роевых алгоритмах для решения оптимизационных задач // Изв. ЮФУ: Технические науки, 2014. № 7. С. 15–25.
8. Кулиев Э.В., Лежебоков А.А. Исследование характеристик гибридного алгоритма размещения // Изв. ЮФУ: Технические науки. 2013. № 3. С. 255–261.
9. Неупокоева Н.В., Курейчик В.М. Квантовые и генетические алгоритмы размещения компонентов ЭВА: монография. Таганрог: Изд-во ТТИ ЮФУ, 2010. 144 с.
10. Курейчик В.В., Запорожец Д.Ю. Современные проблемы при размещении элементов СБИС // Изв. ЮФУ: Технич. науки; Тематич. вып. Интеллектуальные САПР. Таганрог: Изд-во ТТИ ЮФУ, 2011. № 7. С. 68–73.
11. Курейчик В.М. Кажаров А.А. Использование роевого интеллекта в решении NP-трудных задач // Изв. ЮФУ: Изв. ЮФУ: Технич. науки; Тематич. вып. Интеллектуальные САПР. Таганрог: Изд-во ТТИ ЮФУ, 2011. № 7. С. 30–37.