Объектами исследования выбраны системы бионического поиска на основе роевого интеллекта и генетической эволюции для решения задачи планирования перевозок. Планирование перевозок грузов – одна из важнейших функций в системе распределения продукции. Ее математическая модель широко освещалась в литературе под самыми различными названиями: обобщенная  транспортная задача, задача о взвешенном распределении, λ-задача, задача о расстановке флота и др. [1–3].

Основной целью планирования перевозок является повышение эффективности использования транспорта.

Для решения задачи планирования перевозок были предложены различные подходы. В основном это алгоритмы, основанные на эвристиках, обеспечивающих получение приемлемого результата за полиномиальное время [4–8]. Тем не менее, возросшие сложность решаемых задач и требования к качеству решения делают актуальной разработку новых, более эффективных методов. Приведенный анализ разработанных алгоритмов покрытия (последовательных, итерационных и т.д.) показывает, что для создания эффективного алгоритма планирования перевозок, отвечающего современным требованиям, необходимы новые технологии и подходы.

Результатом непрекращающегося поиска наиболее эффективных методов стало использование биинспирированных методов и алгоритмов интеллектуальной оптимизации, базирующихся на моделировании коллективного интеллекта [9]. Анализ методов решения сложных прикладных задач показывает, что применение любого одного алгоритма оптимизации (как классического, так и популяционного) далеко не всегда приводит к успеху. В связи с этим в настоящее время одним из основных путей повышения эффективности методов для решения задач глобального поиска является разработка гибридных алгоритмов [10]. В гибридных алгоритмах преимущества одного алгоритма могут компенсировать недостатки другого. Интеграция метаэвристик популяционных алгоритмов обеспечивает более широкий обзор пространства поиска и более высокую вероятность локализации глобального экстремума задачи [11, 12]. Предлагается композитная архитектура многоагентной системы бионического поиска на основе роевого интеллекта и генетической эволюции.

Постановка задачи. Пусть имеется множество L={ l_j|j=1, 2, …, n} транспортных линий (допустим, пассажирских); по линииl_i нужно выполнить b_j рейсов. В наличии множество D={ d_i|i=1, 2, …, m} транспортных единиц. Резервы полезного времени транспортной единицы d_i составляют a_i. На выполнение транспортной единицей d_i рейса на линииl_j требуется время t_ij, а затраты на рейс составляют c_ij. Требуется указать наиболее экономную расстановку транспортных единиц по линиям [2].

Метод решения задачи планирования перевозок (транспортная задача, задача о взвешенном распределении) построен на допущении, что объемы имеющихся в наличии ресурсов (b_i), требуемые объемы ( a_j) и затраты (c_ij) точно известны.

Обозначая через x_ij количество рейсов, которое транспортная единица d_i должна выполнить по линии l_j, приходим к следующей задаче.

Требуется минимизировать

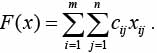                                                  (1)

Искомый набор x_ij должен удовлетворять ограничениям:

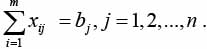                                        (2)

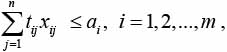                                  (3)

x_ij ≥ 0, i = 1, 2, ..., m, j = 1, 2, ..., n.                                 (4)

При этом соотношения (2) обеспечивают выполнение плана перевозок, а соотношения (3) учитывают ограничения на ресурс транспортной единицы d_i.

Если общий объем наличных ресурсов Σb_j(j = 1, …, n) равен общей потребности в них Σa _i (j=1, …, m), то имеет место сбалансированная (закрытая) распределительная задача. Если же Σa_i≠Σb_j , то задача называется несбалансированной (открытой).

В результате решения задачи планирования перевозок для каждой транспортной линии l_j формируется вектор X_j={x_ij|i=1, 2, …, m}, задающий распределение количества b_j рейсов на транспортной линии l_j между транспортными единицами d_i. Если для некоторого решения X_j задачи распределения не выполняется одно из ограничений (3), то такое распределение считается нелегальным. Общее решение задачи планирования перевозок определяется набором векторов X={X_j | j=1, 2, …, n}.

Общий подход к представлению решений в алгоритме планирования перевозок на основе роевого интеллекта и генетического поиска. В эвристических алгоритмах роевого интеллекта многомерное пространство поиска населяется роем частиц [3]. Каждая частица представляет некоторое решение, в рассматриваемом случае – решение распределительной задачи планирования перевозок. Процесс поиска решений заключается в последовательном перемещении частиц в пространство поиска. Позиция частицы i в пространстве решений в момент времени t (t имеет дискретные значения) определяется вектором x_i(t). По аналогии с эволюционными стратегиями рой можно трактовать как популяцию, а частицу как индивида (хромосому). Это дает возможность построения гибридной структуры поиска решения, основанной на сочетании генетического поиска с методами роевого интеллекта. Связующим звеном такого подхода является структура данных, описывающая решение задачи в виде хромосомы.

Каноническая парадигма роя частиц предусматривает использование вещественных значений параметров в многомерных, вещественных, метрических пространствах. Однако в большинстве генетических алгоритмов гены в хромосомах имеют целочисленные значения. Это не позволяет напрямую использовать каноническую парадигму роя частиц (например, задача направленной мутации одного дерева в направлении другого, с формальной точки зрения, весьма нетривиальна).

В связи с этим актуальной является разработка модернизированной структуры пространства поиска, структуры данных для представления решений и позиций, модернизированных механизмов перемещения частиц в пространстве поиска. Если в качестве частицы используется хромосома, то число параметров, определяющих положение частицы в пространстве решений, должно быть равно числу генов в хромосоме. Значение каждого гена откладывается на соответствующей оси пространства решений. В этом случае возникают некоторые требования к структуре хромосомы и значениям генов. Значения генов должны быть дискретными и независимыми друг от друга, то есть хромосомы должны быть гомологичными.

В работе предлагается подход к построению модифицированной парадигмы роя частиц, обеспечивающей возможность одновременного использования хромосом с целочисленными значениями параметров в генетическом алгоритме и в алгоритме на основе роя частиц.

Принципы кодирования хромосом. Разработка структуры хромосомы производилась так, чтобы гены в одних и тех же локусах хромосом являлись гомологичными, так как это упрощает выполнение генетических операторов. Общее решение планирования перевозок – совокупность векторов X={X_j|j=1, 2, 3, …, n}, X_j={ x_ij|i=1, 2, …, m} представляется в виде совокупности хромосом H={H_j|i=1, 2, …, n}. Каждая H_j соответствует вектору X_j={x_ij|i=1, 2, …, m} и наоборот. Каждая хромосома H_j представляет собой совокупность (m–1) генов g_ij, значения которых могут изменяться в пределах диапазона, определяемого параметром b_j.

Для удобства введено обозначение φ = m–1.

Рассмотрим механизмы кодирования и декодирования на примере одного вектора.

Пусть имеется вектор X_j={ x_ij|i=1, 2, …, m} с фиксированной суммой значений элементов b_j=∑ _i(x_{i j}).

Подобные списки лежат в основе интерпретаций решений в задачах покрытия [14], распределения ресурсов [11, 12] и др.

Хромосома H_j={g_ij| i=1, 2, …, (m–1)} представляет собой совокупность (m–1) генов g_ij, значения которых могут изменяться в пределах диапазона, определяемого параметром b_j:

g_ij 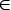H_j, 0 g_ij b_j, i = 1, 2, ..., m.                             (5)

Изначально гены в пределах каждой хромосомы H_j упорядочены по возрастанию их значений.

Процесс перехода от хромосомы H_j к списку осуществляется следующим образом. Сначала гены упорядочиваются по возрастанию их значений, то есть, если g_ij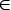H_j и g_i+1,j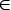H_j, то . Значения g_ij в пределах от 0 до b_j рассматриваются в качестве координат опорных точек на отрезке длиной b_j (от 0 до b_j), разбивающих отрезок на интервалы. Длина интервала между двумя соседними опорными точками и является величиной соответствующего элемента x_ij списка X_j, при этом сумма значений элементов списка X_j равна b_j.

Например. Пусть имеется хромосома H_j={6, 11, 15, 27}, b_j=35, m=5. На отрезке длиной b_j=35 наносятся опорные точки с координатами <0, 6, 11, 15, 27, 35>, разбивающими отрезок на интервалы длиной
< 6, 5, 4, 13, 7>. Эти значения являются значениями списка X_j. X_j =<6, 5, 4, 13, 7>, b_j=35.

Временная сложность декодирования хромосомы, то есть переход от H_j к вектору X_j , имеет линейную зависимость О(m).

Для генетического поиска формируется исходная популяция особей П={ H^k|k = 1, 2, …, θ}, где θ – размер популяции.

Популяция П представляет собой репродукционную группу – совокупность индивидуальностей, каждая из которых может размножаться, выступая в роли родителей.

В работе используется принцип случайного формирования исходной популяции. Для этого в пределах каждой хромосомы Н^к, в каждой части H_j^k, каждый ген принимает случайное значение в диапазоне (0–b_j ), то есть от 0 до b_j.

Кроссинговер К₁ выполняется следующим образом. Пусть имеются две родительские хромосомы – Н¹ и Н². Последовательно просматриваются локусы хромосом, и с вероятностью Р^k_i осуществляется обмен генами в текущем локусе при условии соблюдения ограничения на кроссинговер. Напомним, что в хромосомах H¹_j и H ²_j значения генов упорядочены по возрастанию. Суть ограничения в следующем.

Если текущий локус не является ни первым, ни последним в хромосомах H¹_j и H²_j, то обмен генами g1_i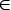H¹_j и g2 _i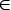H²_j может быть произведен при соблюдении ограничений, имеющих вид:

(g2_li–1 g1_i g2_i+1) и (g1_{i –1}  g2 _i g1_i+1);

(g1_ig2_i+1) и (g2_ig1 _i+1), если локус i является первым в хромосомах Н¹_j  и Н²_j;                         (6)

(g2_i-1 g1_i) и (g1_i-1 g2_l), если локус i является последним в хромосомах Н¹_j  и Н²_j.

Если выполняется одно из ограничений (6), то после обмена генами g1_i и g2_i в новых хромосомах гены будут упорядочены.

Оператор мутации для хромосом второго вида отличается от рассматриваемого выше различными диапазонами возможных значений мутируемого гена, которые регламентируются ограничениями на диапазон.

Если в ходе последовательного просмотра локусов в текущем локусе i выпадает с вероятностью P_м событие «мутация», то ген мутирует. При этом он приобретает случайное значение в диапазоне:

0  g_i  g_i+1, если локус i является первым в части h_i;

g_{l - 1}  g_l  g_l+1, если локусl не является ни первым, ни последним в части h_i; (7)

g_{l- 1} g_lb_i, если локус l является последним в части h_i.

Выполнение ограничений на кроссинговер и на диапазон мутации при выполнении операций кроссинговера и мутации обеспечивает сохранение основного свойства хромосом второго типа, заключающегося в том, что в пределах каждой части Н_i гены упорядочены по возрастанию их значений.

Как видно из алгоритмов, реализующих процедуры кроссинговера и мутации, временная сложность операторов кроссинговера t_k и мутации t_м применительно к одной хромосоме имеют линейную зависимость и оценки временной сложности имеют вид: t_k=О(L), t_м=О( L), где L – длина хромосомы.

Аффинное пространство поиска. Пусть имеется линейное векторное пространство (ЛВП), элементами которого являются n-мерные точки. Каждым любым двум точкам p и q этого пространства однозначным образом сопоставим единственную упорядоченную пару этих точек, которую в дальнейшем будем называть геометрическим вектором (вектором):

p, q 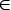V(p,q) – геометрический вектор (упорядоченная пара).

Совокупность всех точек ЛВП, пополненная геометрическими векторами, называют точечно-векторным, или аффинным, пространством. Аффинное пространство является n-мерным, если соответствующее ЛВП также является n-мерным.

Аффинно-релаксационная модель (АРМ) роя частиц – это граф, вершины которого соответствуют позициям роя частиц, а дуги аффинным связям между позициями (точками) в аффинном пространстве. Аффинность – мера близости двух агентов (частиц). На каждой итерации каждый агент p_i переходит в аффинном пространстве в новое состояние (позицию), при котором вес аффинной связи между агентом p_i и базовым (лучшим) агентом p_* уменьшается. Переход агента p_i в новую позицию x_i(t+1) из x_i( t) осуществляется с помощью релаксационной процедуры.

Специальная релаксационная процедура перехода зависит от вида структуры данных (хромосомы): вектор, матрица, дерево и их совокупности, являющейся интерпретацией решений.

Лучшие частицы (и их позиции) с точки зрения целевой функции объявляются «центром притяжения». Векторы перемещения всех частиц в аффинном пространстве устремляются к этим центрам.

Переход возможен с учетом степени близости к одному базовому элементу либо к группе соседних элементов и с учетом вероятности перехода в новое состояние.

Каждую хромосому, описывающую i-е решение популяции, обозначаем как H_i(t)={g_il|l=1, 2, …, n}. Позиция x_i(t) соответствует решению, задаваемому хромосомой H_i(t), то есть x_i (t)=H_i(t)={ g_il|l=1, 2, …, n}. Число осей в пространстве решений равно числу n генов в хромосоме Н_i(t). Точками отсчета на каждой оси l являются дискретные целочисленные значения генов.

Перемещение частиц в пространстве поиска. Пусть имеется рой частиц P={p _k|k=1, 2, …, n_p}. Каждая частица p_k на шаге t размещена в позиции р_k(t).

Введем обозначения:

– р_k(t) – текущая позиция частицы, f_к(t) – значение целевой функции частицы p_k в позиции р _k(t);

– p^*_k(t) – лучшая позиция частицы p_k, которую она посещала с начала первой итерации, а f^* _k(t) – значение целевой функции частицы p_k в этой позиции (лучшее значение с момента старта жизненного цикла частицы p_i);

– p^*(t) – позиция частицы роя с лучшим значением целевой функции f^*( t) среди частиц роя в момент времени t.

Пусть k-е решение X^k={X_j^k|j=1, 2, 3, …, n} задачи планирования перевозок определяется совокупностью векторов X_j^k={x_kij|i=1, 2, …, m}. Позиция p_k(t), соответствующая частице p _k, определяется набором из n хромосом, соответствующим n векторам X_j^k: p_k(t)=Н^k(t)={Н^k_j(t)| j=1, 2, …, n}.

Хромосома Н^k_j(t)={g_kij|i=1, 2, …, (m–1)} представляет собой совокупность (m–1) генов g_kij, значения которых могут изменяться в пределах диапазона, определяемого параметром b_kj:

g_kij 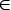H^k_j, 0 g_kij  b_kj.

Пространство поиска включает число осей, равное числу генов в хромосоме Н^k_j(t). Каждому гену в хромосоме Н^k_j( t) соответствует ось (номер оси). Точками отсчета на каждой оси OX_i являются целые числа в интервале от 0 до b_kj.

Перемещение частицы p_k из позиции p_k(t) в позицию p_k(t+1) под воздействием притяжения к позицииp_z(t) осуществляется путем применения оператора направленной мутации (ОНМ) к хромосомам позиции p_k(t) следующим образом.

В качестве оценки степени близости между двумя хромосомами Н^k_j(t)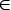Н^k(t) и Н^z_j(t)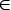Н^z(t) будем использовать величину S_kzj расстояния между хромосомами Н^k_j(t) и Н^z_j(t):

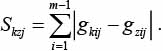                               (8)

В качестве оценки степени близости между двумя позициями Н^k(t) и Н^z(t) используется величина расстояния между Н^k(t) и Н^z( t):

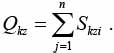                                         (9)

Суть процедуры перемещения, реализуемой ОНМ, заключается в изменении разности между значениями каждой пары генов ( g_kij , g_zij) двух хромосом Н^k_j(t) и Н^z_j(t): i=1, 2, …, m–1; j=1, 2, …, n.

Последовательно просматриваются (начиная с первого) локусы хромосом Н^k_j(t) и Н^z_j(t), и сравниваются соответствующие им гены. Если в ходе последовательного просмотра локусов в текущем локусе i выпадает с вероятностью P событие «мутация», то ген g_kij 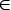Н ^k_j(t) мутирует.

Пусть R_kzi(t) – число локусов в хромосомах Н^k_j(t) и Н^z_j(t), в которых значения генов g_kil(t)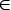Н^k_j(t) и g_zil(t)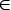Н^z _j(t) не совпадают.

Вероятность π мутации в хромосоме Н^k_j(t) зависит от числа R_kzj(t) несовпадений между значениями генов и определяется следующим образом:

π=α× R_kzj(t)/( m–1),                                (10)

где α – коэффициент, а (m–1) – длина хромосомы. Таким образом, чем больше число R_kzi(t) несовпадающих генов между хромосомами Н^k_j(t) и Н^z_j(t), тем более вероятно, что значение g_kij(t)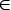Н ^k_j(t) будет изменено.

Простой лотереей L (1, π, 0) назовем вероятностное событие, имеющее два возможных исхода – 1 и 0, вероятности наступления которых обозначим, соответственно, через π и (1–π). Другими словами, с вероятностью π лотерея L(1, π, 0)=1, а с вероятностью (1–π) лотерея L(1, р, y₂)=0_. Значения генов новой позиции частицы р _k(t+1) в результате мутации определяются как

g_kij (t+1)= g_kij(t), если (g_kij(t) = g_zij(t));

g_kij (t+1)= g_kij (t)+L (1, π, 0), если (g_kij(t)< g_zij(t));                              (11)

g_kij (t+1)= g_kij(t) –L (1, π, 0), если (g_kij(t)> g_zij(t)).

Пример. Пусть b_kj=23, m=6, Н^k_j(t) =<1, 2, 4, 8, 8>, X^k_j( t) =<1, 1, 2, 4, 0, 15>,

Н^z _j (t) =<3, 3, 4, 6, 7>, X^z _j(t) =<3, 0, 1, 2, 1, 16>,

S_kzj (t)=6.

Пусть с некоторой вероятностью в Н^k _j(t) мутировали гены в 1-м и 4-м локусах. В результате направленной мутации

Н ^k _j (t+1) =<2, 2, 4,7, 8>, X ^k_j(t+1) =<2, 0, 2, 3, 1, 15>,

S_kzj (t+1)=4.

Для учета одновременного тяготения частицы р_k(t) к лучшей позиции р _k(t)^* среди частиц роя в момент времени t и к лучшей позиции р_k(t)^* частицы р_k(t), которую она посещала с начала первой итерации, формируется виртуальный центр (позиция) притяжения р_k(t)^c частицы р_k(t). Формирование виртуальной позиции р_k(t)^c осуществляется путем применения процедурывиртуального перемещения из позиции р _k(t)^* в виртуальную позицию р_k(t)^c по направлению к позиции р _k(t)^*. После определения центра притяжения р_k(t) ^c частица р_k(t) перемещается в направлении виртуальной позиции р_k(t)^c из позициир_k(t) в позицию р_k(t+1). После перемещения частицы р_k(t) в новую позицию р_k(t+1) виртуальная позиция x^c_i(t) исключается. Локальная цель перемещения частицы p _i – достижение ею позиции с наилучшим значением целевой функции. Глобальная цель роя частиц – формирование оптимального решения задачи.

Механизмы генетического поиска. На первом этапе гибридного алгоритма выполняется генетическая эволюция популяции позиций П={X^k|k=1, 2, …, K}, в которых помещен рой частиц
P= {p_k|k=1, 2, …, K}. На каждой генерации вначале реализуются операторы кроссинговера, мутации, а затем расширенная популяция подвергается редукции с помощью селективного отбора, то есть уменьшению до начального объема.

Основными генетическими операторами являются кроссинговер и мутация [11]. Структура кроссинговера в основном определяет эффективность ГА.

Поскольку хромосомы гомологичны, кроссинговер выполняется путем взаимного обмена генами между парой хромосом в случайно выбранных локусах.

Каждая хромосома позиции подвергается мутации.

Оператор мутации выполняется путем изменения взаимного расположения двух (случайно выбранных) генов в хромосоме. Затем на основе популяции, полученной на последней итерации генетического поиска, формируется популяция для роевого алгоритма. В формируемую популяцию включаются лучшие, но отличные друг от друга хромосомы. При необходимости полученная популяция доукомплектовывается новыми индивидами. После этого дальнейший поиск решения осуществляется роевым алгоритмом.

При втором подходе метод роя частиц используется в процессе генетического поиска и играет роль, аналогичную генетическим операторам. В этом случае на каждой итерации генетического алгоритма синтез новых хромосом осуществляется с помощью, с одной стороны, кроссинговера и мутации, а с другой – операторов направленной мутации (ОНЦ) методами роя частиц.

Как видно из алгоритмов, реализующих процедуры кроссинговера и мутации, временная сложность операторов кроссинговера и мутации применительно к одной хромосоме имеют линейную зависимость оценки временной сложности.

Экспериментальные исследования. Целью исследований являлось определение эффективности интеграции роевого и генетического алгоритмов. Для этого сначала по отдельности проводились исследования роевого и генетического алгоритмов, разработанных авторами. А затем исследовался гибридный алгоритм.

Исследованию подвергались примеры задач планирования перевозок на сети транспортных линий размером от 20 до 100, обслуживаемых множеством транспортных единиц размером от 5 до 15. Каждый пример тестировался на 20 независимых прогонах генетическим, роевым и гибридным алгоритмами по отдельности.

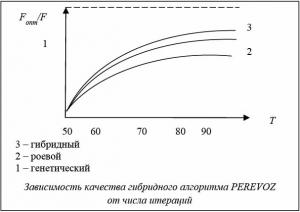
При исследовании сходимости алгоритмов для каждого эксперимента запоминался номер генерации, после которой не наблюдалось улучшения оценки. В каждой серии из 20 испытаний определялись среднее значение числа генераций, после которого не наблюдалось улучшения оценки. Для каждой серии испытаний определялось лучшее решение. На основе обработки экспериментальных исследований для алгоритмов была построена средняя зависимость качества решений от числа итераций.

Исследования показали, что число итераций, при которых алгоритм находил лучшее решение, лежит в пределах 110–130. Алгоритм PEREVOZ сходится в среднем на 125-й итерации (см. рисунок). Эксперименты показали, что увеличение популяции М больше 120 нецелесообразно, так как это не приводит к заметному изменению качества.

В результате проведенных исследований установлено, что качество решений у гибридного алгоритма на 10–15 % лучше качества решений генетического и роевого алгоритмов по отдельности.

Сравнение значений критерия, полученных гибридным алгоритмом на тестовых примерах с известным оптимумом, показало, что вероятность получения глобального оптимума составила 0,96. В среднем результат, полученный предложенным алгоритмом на 130-й итерации, отличается от точного на 0,15 %. В среднем запуск программы обеспечивает нахождение решения, отличающегося от оптимального, менее чем на 2 %.

Сравнение с известными алгоритмами показало, что при меньшем времени работы у полученных с помощью разработанного алгоритма решений отклонение целевой функции от оптимального значения меньше в среднем на 6 %.

Задачи, на которых был протестирован разработанный алгоритм, доступны в библиотеке OR-объектов (http://www.ms.ic.ac.uk/info.html) [15–17]. Временная сложность алгоритма при фиксированных значениях M и T лежит в пределах О(n). Общая оценка временной сложности практически совпадает с теоретическими исследованиями и для рассмотренных тестовых задач лежит в пределах О(n²)–О(n³).

Заключение . Предложена композитная архитектура многоагентной системы бионического поиска на основе интеграции роевого интеллекта и генетической эволюции для решения задачи планирования перевозок. Связующим звеном такого подхода является единая структура данных, описывающая решение задачи в виде хромосомы. Интеграция метаэвристик популяционных алгоритмов обеспечивает более широкий обзор пространства поиска и более высокую вероятность локализации глобального экстремума задачи.

Ключевая проблема, которая была решена в данной работе, связана с разработкой структуры аффинного пространства позиций, позволяющей отображать и осуществлять поиск интерпретаций решений с целочисленными значениями параметров. В отличие от канонического метода роя частиц для уменьшения веса аффинных связей путем перемещения частицы p_i в новую позицию аффинного пространства решений разработан оператор направленной мутации, суть которого заключается в изменения целочисленных значений генов в хромосоме. Разработаны новые структуры хромосом для представления решений.

Разработанный алгоритм планирования перевозок имеет универсальный характер и может использоваться для решения широкого круга комбинаторных задач линейного целочисленного программирования. Эксперименты показали, что качество решений, полученных гибридным алгоритмом, на 10–15 % лучше, чем у генетического и роевого алгоритмов. Вероятность получения глобального оптимума составила 0,9. Общая оценка временной сложности при любом подходе к гибридизации лежит в пределах О(n²)–О( n³) и не превышает оценки временной сложности генетического алгоритма.

Работа выполнена при финансовой поддержке гранта РФФИ № 18-07-00737.

Литература

1. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. М., 2004. 234 с.

2. Андерсон Д. Дискретная математика и комбинаторика. М.: Вильямс, 2003. 305 с.

3. Корниенко В.П. Методы оптимизации. М.: Высш. шк., 2007. 189 с.

4. Brucker P. Scheduling algorithms (5th ed.). Springer, 2007, pp. 345 –357.

5. Peter B. Scheduling algorithms. Springer-Verlag Berlin Heidelberg, 2006, pp. 48–59.

6. Серая О.В. Распределительная задача линейного программирования // Системы обработки информации. 2013. № 2. С. 167–170.

7. Акулич И.Л. Математическое программирование в примерах и задачах. Лань, 2011. 190 с.

8. Пантелеев А.В., Скавинская Д.В., Алёшина Е.A. Метаэвристические алгоритмы поиска оптимального программного управления. М.: ИНФРА-М, 2017. 168 с.

9. Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой. М.: Изд-во МГТУ им. Н.Э. Баумана, 2014. 459 с.

10. Wang X. Hybrid nature-inspired computation method for optimization. Thesis Doct. Dis. Helsinki Univ. of Technology, Espoo, 2009, 577 р.

11. Лебедев Б.К., Лебедев В.Б. Планирование на основе роевого интеллекта и генетической эволюции // Изв. ЮФУ. 2009. № 4. С. 25–33.

12. Лебедев Б.К., Лебедев О.Б., Лебедева Е.М. Распределение ресурсов на основе гибридных моделей роевого интеллекта // Науч.-технич. вестн. ИТМО. 2017. Т. 17. № 6. С. 1063–1073.

13. Kennedy J., Eberhart R.C. Particle swarm optimization. Proc. IEEE Intern. Conf. on Neural Networks, 1995, pp. 1942–1948.

14. Лебедев Б.К., Лебедев В.Б. Покрытие методом роя частиц // Интегрированные модели и мягкие вычисления в искусственном интеллекте: матер. VI Междунар. науч.-практич. конф. М.: Физматлит, 2011. С. 611–619.

15. Beasley J.E. Distributing test problems by electronic mail. JORS, 1990, pp. 1069–1072.

16. Job shop scheduling benchmarks, URL: OR Library online, http://mscmga.ms.ic.ac.uk (дата обращения: 18.08.2018).

17. J. Romesis Cong M. and Xie M. Optimality, scalability and stability study of partitioning and placement algorithms, Proc. Intern . Sympos. on Physical Design, Monterey, CA, 2003, pp. 88–94.