Основным и широко распространенным техническим средством, используемым для измельчения руды перед ее обогащением, являются шаровые мельницы. Они отличаются большими габаритами и массой, а также высокой стоимостью (рис. 1). Как правило, это главный орган обогатительной фабрики, который определяет и ограничивает ее производительность [1].

После крупного, среднего и мелкого дробления руда поступает в цех мельнично-флотационного отделения для дальнейшего измельчения. Все технологическое оборудование связано системой конвейерных линий, обеспечивающих нормальную работу комплексов измельчения.

Дробленая руда из разгрузочных бункеров с помощью ленточных конвейеров питателями равномерно распределяется на наклонные конвейеры (рис. 2). С наклонных конвейеров руда через улитковые питатели (хоботы), проходя по спиральной полости, попадает в корпус барабана мельницы. Под действием возникающих сил (в результате падения металлических шаров) внутри барабана происходит дальнейшее измельчение. Готовый подрешетный продукт измельчения, проходя через систему сепарации, подается по трубопроводу с помощью насосов на процесс флотации.

Производительность мельницы при достижении одной и той же крупности помола зависит от крупности подаваемого в нее материала и возрастает при уменьшении его крупности. В то же время крупность используемых в мельнице шаров зависит от крупности подаваемой на помол руды. Наибольшая производительность мельниц достигается при подаче в них мелкодробленой руды с крупностью зерен до 3–5 мм. При такой крупности измельчаемой руды нет необходимости подавать в мельницу крупные шары, что способствует снижению износа защитного покрытия барабана мельницы.

Для защиты барабанов МШР-3,6×4,0 и МШР-4,5×5,0, входящих в комплексы измельчения на обогатительной фабрике, от изнашивающего и разрушающего воздействия шаров и измельчаемого материала в настоящее время применяются сменные футеровочные элементы: бронеплиты цилиндрической поверхности барабана, торцевая бронь, разгрузочная решетка и футеровка цапф – загрузочный патрубок и разгрузочная воронка.

При создании наиболее эффективной системы диагностики оборудования, входящего в комплекс измельчения, необходимо учитывать состояние защитной футеровки барабанов мельниц. Износ футеровки (в допустимых пределах) приводит к увеличению объема барабана мельницы, что влияет на производительность комплекса измельчения. Диагностика необходима для своевременного вывода мельницы в ремонт и предотвращения аварийного износа защитной футеровки.

Срок службы защитной футеровки как детали, наиболее полно влияющей на эксплуатационные показатели мельницы, является определяющим параметром при формировании структуры ремонтного цикла агрегата измельчения.

С экономической точки зрения наиболее целесообразным будет вариант, при котором срок службы футеровки цилиндрической части барабана равняется сроку службы торцевой футеровки, разгрузочной решетки. В этом случае перефутеровка всей мельницы производится одновременно, сокращаются трудозатраты и время простоя. В настоящее время, основываясь на практических данных, можно говорить, что торцевая бронь и решетка выдерживают установленный ресурс в 8640 м/ч, чего нельзя сказать о футеровке цилиндрической части барабанов МШР.

В целях уточнения ремонтных нормативов должен вестись систематический учет фактического времени работы и простоя основного оборудования. По мере необходимости представляются обоснованные предложения по применению данных нормативов.

К числу показателей, существенно влияющих на интенсивность износа защитной футеровки горно-обогатительного оборудования, относятся следущие:

– свойства стали футеровок;

– степень абразивного износа;

– свойства стали и размеры мелющих тел;

– профиль футеровки;

– размеры барабана мельницы;

– схема измельчения и классификации;

– оптимальное пульповое наполнение.

Материал футеровки должен иметь высокую ударную вязкость, абразивную стойкость, стойкость под ударными нагрузками и постоянство свойств в процессе работы. Наиболее полно этим требованиям удовлетворяет высокомарганцевая сталь 110Г13Л, применяющаяся в качестве материала футеровок МШР и по настоящее время. Комплекс механических и эксплуатационных характеристик изделий из стали 110Г13Л в значительной степени зависит от содержания в ней примесей, тщательного соблюдения технологии литья, закалки и температурных режимов при этих операциях, модифицирования, легирования, выбора рациональных конструкций литых деталей. К настоящему моменту нельзя говорить о том, что в литейном производстве, поставляющем защитную футеровку, произошли какие-либо изменения в части повышения износостойкости стали 110Г13Л.

Степень абразивного износа защитной футеровки находится в прямой зависимости от абразивности, крупности и крепости измельчаемого материала. За последние годы наблюдается тенденция снижения содержания полезных компонентов в исходной руде, вовлечение в производство трудно измельчаемых руд. Также существенным фактором, влияющим на износ футеровки, является процентное заполнение барабана мелющими телами и удельное соотношение типоразмеров шаров. Для апатитонефелиновых руд оптимальное шаровое наполнение мельниц составляет 48 %.

В значительной степени определяет срок службы футеровки ее профиль. В настоящее время применяется «волновой» (с одной волной) профиль с наибольшей толщиной по гребню для МШР 3,6×4,0–120 мм, для МШР 4,5×5,0–150 мм. Выбор применения той или иной профильной конструкции футеровки должен производиться с учетом типа, расхода и режимов работы измельчающей среды, физико-механических свойств размалываемого материала, производительности и эффективности работы мельницы, удельных расходов энергии, стоимости материалов и величины эксплуатационных расходов.

За последние годы существенно изменились факторы, определяющие условия работы агрегатов мокрого измельчения: внедрение барабанов новых типоразмеров, изменение физико-механических свойств перерабатываемой руды, изменение технологических параметров процесса измельчения и т.д.

Защитная футеровка барабанов мельниц подвергается большей степени износа и установленный межремонтный период (ресурс) в 8640 м/час не выдерживает. Снижение ресурса износостойкости защитной футеровки подтверждается количественными данными о замене футеровок при проведении ремонтов, при аварийных остановках в течение 5-6 межремонтных циклов (то есть после достижения мельницей пробега в 5760 м/ч).

В работе [2] предложено несколько возможных рекомендаций по изменению графика планово-предупредительного ремонта мельниц для оптимального использования бронеплит и выдерживанию времени межремонтных интервалов, в том числе и план, разработанный на базе модели данного исследования, когда диагностика происходит в процессе работы и остановка агрегата осуществляется только при достижении оценок докритических величин.

Механизм управления

Отправной точкой предлагаемого механизма предупреждения является тот факт, что только одна методика не может быть абсолютно достоверной в рамках диагностики рассматриваемой системы или агрегата. Сигналы, выдаваемые одной системой мониторинга, должны иметь подтверждение от другой, альтернативной, основанной на ином подходе, возможно, другом математическом аппарате.

Сигналы, снимаемые датчиками с технологического оборудования, по своей природе носят нестационарный характер. Для анализа будущего развития таких сигналов, а значит, и характеристик работы агрегатов и систем, необходимо использовать комплексный подход [3, 4].

Параметры технологического оборудования по своей природе чаще всего носят нестационарный характер. Предлагается рассматривать параметр оборудования как комплексный сигнал, состоящий из конечных временных интервалов, в рамках которых динамика процесса относительно постоянна, и моменты времени, в которые происходит так называемый фазовый переход системы из одного устойчивого состояния в другое, что обусловлено нестационарностью сигнала и системы по своей природе (рис. 3).

Для отслеживания и прогнозирования будущего развития состояния системы внутри временных интервалов стационарности, выраженного множеством состояний оборудования, используется аппарат теории случайных процессов, а именно стохастический процесс с непрерывным временем модели Маркова, которая с успехом используется во многих областях для описания систем с заданными свойствами.

Для предупреждения фазового перехода (кардинальной смены тенденции, аварии) применяется альтернативная методика из области статистической физики и критических явлений.

Данные методы с успехом применяются для описания поведения систем и моделирования околофизических явлений во множестве приложений. Это различные критические явления: лавины, землетрясения, описание поведения таких сложных систем, как рынки, перколационные модели в физике [5].

Модель стационарных состояний технологической системы комплекса измельчения

Рассмотрим классификацию возможных состояний комплекса измельчения. Выделим четыре возможных состояния: исправное состояние агрегата, работоспособное, неработоспособное, аварийное.

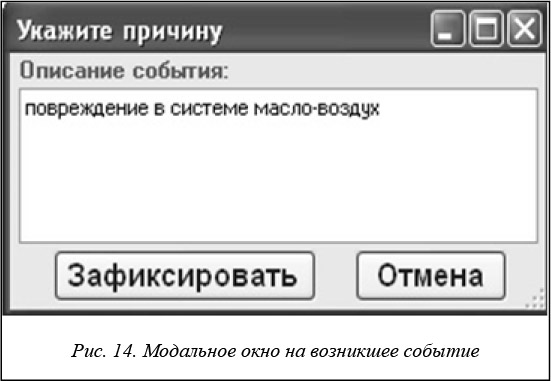
В исправном состоянии все элементы комплекса измельчения (далее мельницы) находятся в исправном, то есть рабочем состоянии. Работоспособное состояние характеризуется тем, что один или несколько элементов находятся в нерабочем состоянии, но агрегат продолжает функционировать (например, повреждение трубки подачи масла). Таким образом, система может перейти из исправного состояния в работоспособное в результате повреждения (рис. 4).

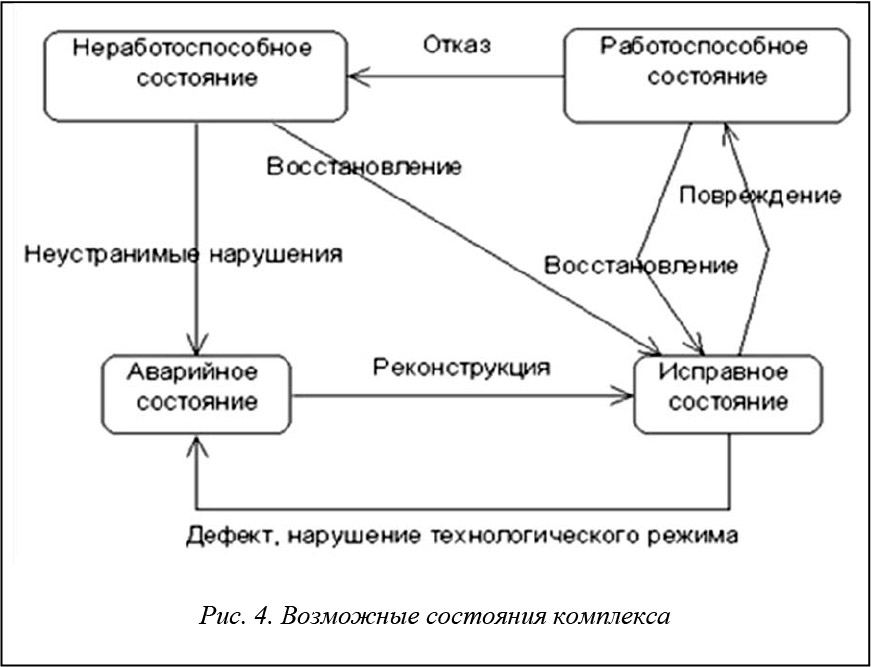
При проведении ремонта (восстановлении) поврежденных узлов либо их замене мельница может снова из работоспособного состояния вернуться в исправное.

Очевидно, если система однажды попала в работоспособное состояние, увеличивается вероятность оказаться в неработоспособном. Это может произойти в результате возникновения отказов по цепочке, когда на одном из этапов система не может функционировать и останавливается на ремонт, либо настало время планового осмотра (ремонта). Из неработоспособного состояния агрегат в результате проведения процедур восстановления сразу переходит в исправное состояние.

В аварийное состояние система может попасть как из полностью исправного состояния, так и из неработоспособного. Аварийное состояние возникает при неустранимых нарушениях и ведет к длительной остановке всей системы. Повреждения связаны с разрушением внутренних плит футеровки, которые защищают внутреннюю часть корпуса мельницы от разрушительного действия ее «начинки».

В процессе работы происходит постепенное изнашивание плит из-за сил трения и, главным образом, из-за систематических ударов быстрых подвижных элементов внутри. Это приводит к полному либо частичному раздроблению плит футеровки (рис. 5). Чтобы не допустить повреждения корпуса в случае разрушения защитной плиты, на производстве периодически производится останов мельницы.

Построим для данной системы дифференциальные уравнения Колмогорова:

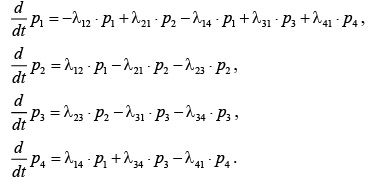
Интегрируя по времени, находим вероятности состояний для каждого состояния как функции времени:

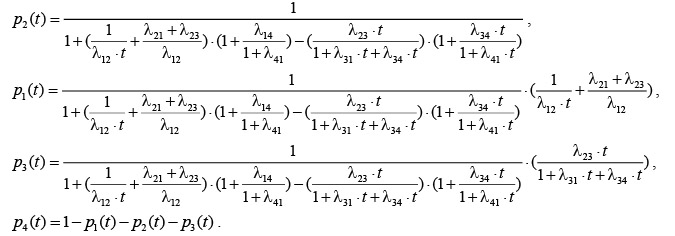
Введем понятие предельной вероятности состояний для системы S. Предположим, что все интенсивности потоков событий, переводящих систему из состояния в состояние, постоянны, то есть l_ij = const.

Записав систему дифференциальных уравнений Колмогорова для вероятностей состояний и проинтегрировав эти уравнения при заданных начальных условиях, получим вероятности состояний как функции времени при любом t, дающие в сумме единицу .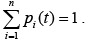

Рассмотрим, что будет происходить с системой S при t ®¥. Функции , P₂(t), …, P_n( t) будут стремиться к пределам, называемым предельными (финальными) вероятностями состояний. Если число состояний системы S конечно и из каждого состояния можно перейти (за то или иное число шагов) в каждое другое, то предельные вероятности состояний существуют и не зависят от начального состояния системы.

Предположим, что поставленное условие выполнено и предельные вероятности существуют: , (i=1, 2, ..., n).

Таким образом, при t ®¥ в системе S устанавливается некоторый предельный стационарный режим. Он состоит в том, что система случайным образом меняет свои состояния, но вероятность каждого из них уже не зависит от времени: каждое из состояний осуществляется с некоторой постоянной вероятностью. Эта вероятность представляет собой не что иное как среднее относительное время пребывания системы в данном состоянии. Например, если у системы S три возможных состояния: S1, S2, S3, причем их предельные вероятности равны 0,2; 0,3 и 0,5, то это означает, что после перехода к установившемуся режиму система S в среднем две десятых времени будет находиться в состоянии S1, три десятых – в состоянии S2 и половину времени – в состоянии S3.

В предельном (установившемся) режиме все вероятности состояний постоянны, значит, их производные равны нулю, то есть для вычисления предельных вероятностей состояний системы в системе уравнений Колмогорова нужно положить все левые части (производные) равными нулю. В этом случае система дифференциальных уравнений превратится в систему линейных алгебраических уравнений. Совместно с нормировочным условием эти уравнения дают возможность вычислить все предельные вероятности: P₁, P₂, …, P_n.

Рассмотрим систему, представленную размеченным графом на рисунке 4. Для данного графа условие существования предельных вероятностей выполняется, так как из каждого состояния системы S можно перейти (за конечное число шагов) в любое другое. Приравнивая нулю производные в уравнениях Колмогорова, получаем:

В марковском случайном процессе его будущее развитие зависит только от настоящего состояния и не зависит от предыстории процесса, то есть от развития процесса в прошлом. Если рассматривать некоторое техническое устройство в реальности, характеристики работы системы в будущем, очевидно, будут зависеть не только от текущего состояния агрегата, но и от того, насколько он уже «износился» в процессе эксплуатации до данного момента времени. Эта зависимость в некоторой степени исчезает при рассмотрении «чисто» вероятностных систем, то есть когда будущие состояния определяются некоторыми случайными факторами [6, 7].

Таким образом, если рассматриваемый реальный процесс заменяется моделью Маркова, значит, можно утверждать, что строится вероятностная модель процесса и рассматриваемый реальный процесс с некоторыми допущениями можно считать таковым.

Предполагается, что процесс в технологической системе носит стационарный и эргодический характер своего развития (почти всюду).

Коснемся вопроса о допущениях для технического агрегата или технологического комплекса. Рассмотрим математическую модель технического устройства, представляющую марковскую однородную цепь, заданную своим графом состояний и матрицей вероятностей переходов (рис. 6).

В период временной стационарности система будет совершать переходы в некотором множестве состояний M1, сгруппированных на рисунке в левой части от пунктирной линии. Если система в результате нелинейности своего поведения совершает скачок в правое множество состояний M2 и начинает работать там на протяжении некоторого времени, статическая матрица P марковской цепи уже не учитывает новый сценарий поведения адекватно, так как отражает некоторое усредненное распределение для данных двух классов состояний (M1, M2) как результат, неточность предсказания будущего поведения. Количество классов (множеств) состояний равно двум для упрощения изложения, в реальности таких устойчивых классов можно выделить больше.

В некоторой степени улучшить модель позволяет использование неоднородной марковской цепи либо модели с непрерывным временем, если переходы осуществляются асинхронно, что более точно отражает работу технического агрегата.

При таком подходе матрица вероятностей

P(t) переходов изменяется динамически во времени, и, чем дольше времени система находится в одной из частей графа, тем ближе будет «расположена» матрица к реальному положению дел в системе (рис. 7).

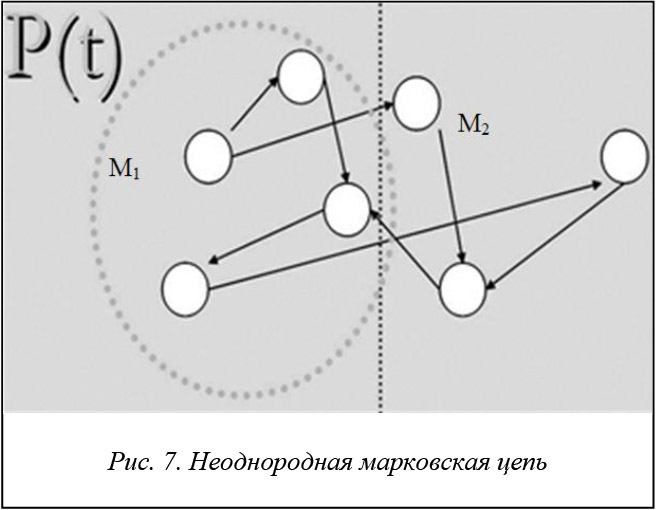
Приведенный пример системы с двумя множествами состояний можно ошибочно идентифицировать как процесс с двумя эргодическими классами (возможно, периодическими). Далее приводятся рассуждения авторов в контексте реального производства. В примере выделены два множества состояний, которые отражают временные интервалы стационарности. Возникающая нелинейность в работе технического агрегата заставляет его совершить переход во второе множество состояний, которое можно определить как его предаварийное либо аварийное множество (например, возникающие цепочечные отказы, когда отказ одного узла ведет к отказу второго, отказ второго – к отказу третьего и так далее, возможно, до полного останова агрегата – аварии). Очевидно, что состояние, попав во второе множество, необязательно в реальности приведет к тому, что это множество окажется поглощающим. Если бы это было так, то при t ® ¥ агрегат всегда, попав во второе множество, оказывался бы либо в предаварийном, либо в аварийном состоянии. Но так как на реальном производстве имеются обслуживающий персонал и системы технической диагностики, агрегат, попав во второе множество, имеет высокие шансы попасть обратно в первое множество и продолжить работу в штатном режиме. Таким образом, ни одно из двух множеств состояний не может быть поглощающим. Система (агрегат) асинхронно может оказаться как в первом множестве, так и во втором и совершать между ними переходы в произвольные моменты времени. Последнее утверждение противоречит определению эргодического класса, которое гласит, что, однажды попав в такое множество состояний, система никогда уже не покинет его. Также это противоречит определению периодического эргодического класса, так как возврат из одного множества состояний в другое (из одного класса в другой) происходит асинхронно.

Процесс, имеющий более одного эргодического класса, уже не будет эргодическим, что противоречит сделанным допущениям о допустимости использования марковских моделей. Только при наличии точно одного эргодического класса марковский процесс будет эргодическим. Действительно, независимо от начального состояния система в конце концов попадет в этот класс и будет совершать переходы между его состояниями. Однако если процесс имеет два или более эргодических классов, то свойство эргодичности не выполняется; если система выходит из какого-либо состояния одного класса, то она будет совершать переходы внутри него и никогда не попадет в другой класс состояний. В этом смысле каждый эргодический класс является обобщенным поглощающим состоянием: попав в него однажды, система не может его покинуть.

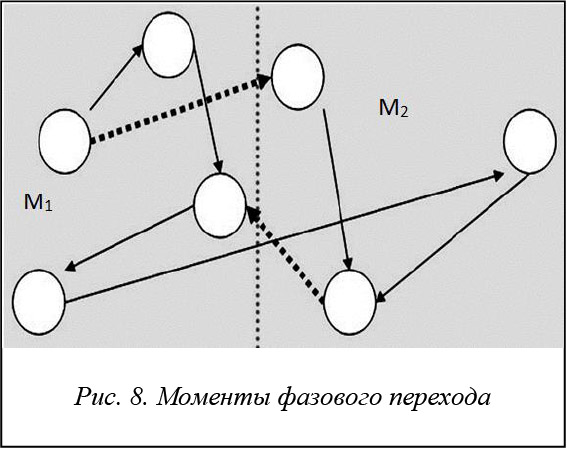
Таким образом, на данном этапе выявляется главный недостаток (ограничение, свойство) любой марковской модели. Ни одна марковская модель не учитывает моменты переходов из одного подграфа к другому, так как сама носит только вероятностный характер описания системы, а момент такого перехода не может быть ей известен. Эти переходы показаны пунктирными стрелками на рисунке 8.

В конструируемой математической модели марковской модели отводится роль описания системы внутри интервалов времени, в которых система носит стационарный характер своего поведения, то есть внутри временных интервалов стационарности (множество 1 в приведенном примере). Множество 2 (второе множество, класс состояний – предаварийное, аварийное) также присутствует в графе марковской модели, но вероятностная оценка перехода во второе множество (пунктирные стрелки на рисунке 8) подконтрольна другой модели – модели фазовых переходов статистической физики, которая будет рассмотрена далее.

Таким образом, в системе мониторинга должна присутствовать процедура (некая нелинейная подмодель) отслеживания с некоторой вероятностью момента перехода (скачка) системы из одного стационарного состояния в другое, которая рассматривается далее.

Метод обнаружения фазового перехода системы в случае нестационарного сценария поведения технологического оборудования

Из обобщенного (универсального) класса «технологическая система» можно выделить подкласс (подмножество) «многоагентная технологическая система». Такой объект представляет собой множество, которое включает в себя большое количество элементарных элементов (агентов) с некоторыми свойствами (заданными статистически по результатам оценок для данного объекта). Следующим свойством объекта является наличие некоторого механизма взаимодействия между элементами множества. Механизм взаимодействия, как и механизм появления и исчезновения элементарных взаимодействий, между отдельно взятыми элементами проследить не представляется возможным. Можно сделать вывод, что рассматриваемый объект представляет собой сложную систему. Для построения модели такого объекта существуют три базовых подхода:

– макроскопический (анализируются свойства системы как единого целого);

– микроскопический (исследователь проникает в механизм взаимодействия элементарных агентов и обобщает полученный результат на всю систему);

– топологический (строится графоподобная модель взаимодействия элементарных агентов и далее обобщается для количества элементов N ® ¥).

В последнее время намечается тенденция, когда для создания более точной модели результаты, полученные в одном из методов, становятся входными данными (аргументами) в уравнениях, полученных по другому методу. Таким образом, намечается не объединение данных методов, а их взаимодополнение с целью разработки качественно новой модели, так как характеристики, полученные в одном из методов, не могут быть получены из другого и наоборот.

Основная гипотеза состоит в том, что аварии вызываются усилением медленно нарастающих низкочастотных корреляций в поведении агентов, приводя к коллапсу системы в критической точке. На языке математики сложные системы в своем поведении могут проходить точки, определяемые как взрывоподобный рост некоторых величин, которые в обычных условиях ведут себя достаточно плавно. Обычно для нелинейных динамических систем существование критических точек является правилом, нежели исключением. Отмечая своеобразный характер возникновения аварий и повреждений технологического оборудования, можно сравнить их с фазовыми переходами известных из физики критических явлений.

Предлагаемый подход основан на положении, что вся информация о прошлых состояниях и будущих ожиданиях работоспособности агрегата или системы полностью «сокрыта» и уже содержится в значениях временных рядов технологических параметров показаний датчиков, считываемых с объекта.

Когда технологическая система или агрегат начинают функционировать в предаварийном состоянии, параметры этого объекта строят сигнатуры, которые интерпретируются в теории критических явлений как потеря устойчивости. При определенных условиях значительно возрастает вероятность того, что технологическая система выйдет из состояния равновесия и перейдет в новое устойчивое состояние, например аварийное, со значительным изменением технологических параметров функционирования. В этом случае произойдет фазовый переход, означающий для технического агрегата потерю его работоспособности. Данные сигнатуры зарождаются в технологических параметрах как предвестники аварии и представляют собой некоторую структуру, которая зарождается в ряде. Правильно идентифицировав данную структуру, с некоторой долей вероятности можно утверждать, что данный переход может произойти в ближайшем будущем.

Описание модели обнаружения фазового перехода и получение функции-сигнатуры

Обоснованность применения модели базируется на свойствах, которым должна удовлетворять производственная система:

– в системе должно присутствовать большое количество элементов;

– элементы характеризуются множеством возможных воздействий;

– взаимодействие отдельных элементов дает суммарную величину, известную как потенциал всей системы;

– в зависимости от уровня общего потенциала отдельные элементы воздействуют на систему определенным образом.

Эти требования общие, будем исследовать систему в рамках указанных предположений при отсутствии внешних воздействий, то есть изолированную систему. Сначала рассмотрим вариант теории среднего поля, потом сформулируем микроскопическую модель.

Можно предположить, что при данных свойствах система будет стремиться минимизировать некоторую потенциальную функцию. Это означает, что в отсутствие внешних возмущений система стремится к состоянию равновесия, которому соответствует минимум энергии некоторого силового поля (рис. 9), причем природа этого поля может быть различной [8].

Макроскопический подход . В духе среднего поля для коллективных систем простейший подход для описания имитационных процессов состоит в предположении, что скорость наступления аварии (краха) h(t) управляется уравнением

,

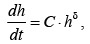где d > 1; C – положительная константа. Приближение среднего поля заменяет действие всего множества элементов неким усредненным поведением, на которое ориентируются остальные элементы. В этом смысле h(t) есть результат взаимодействия между всеми элементами. Член h ^d как раз и описывает это взаимодействие. Интегрируя уравнение, получаем

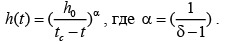, где .

Отсюда видно, что величина d должна быть больше единицы для роста h(t) при приближении к точке фазового перехода. Параметр a должен лежать в диапазоне от 0 до 1 по технологическим причинам, в противном случае технологический параметр уйдет на бесконечность.

Микроскопический подход. Рассмотрим сеть элементов, помеченных индексом i = 1, 2, …, N, и выделим набор элементов, связанных с рассматриваемым элементом посредством некого механизма. Отдельный элемент системы может пребывать в определенном состоянии. Предположим, что состояния элемента i определяются уравнением

,

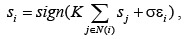где функция sign(×)равна +1 и -1; K – положительная константа, e_i – нормально распределенная случайная величина. Это уравнение относится к классу стохастических динамических систем, описывающих ансамбль взаимодействующих частиц. Такие модели активно изучаются в физике магнетизма, математике и биологии. Здесь тенденция к имитации отдельных элементов описывается константой K, тенденция к случайному поведению – s. Таким образом, отношение K к s определяет борьбу между порядком и беспорядком во временной последовательности и вероятность аварии (фазового перехода). Можно выбрать много величин, описывающих ансамбль элементов как целое. Одной из величин, описывающих ситуацию, когда большая группа элементов находится в состоянии сильной коррелированности (ведут себя одинаково), является восприимчивость системы. Для ее определения в предыдущее уравнение введем новый глобальный параметр влияния G:.

Этот параметр будет устанавливать состояния всех элементов, равных +1, если G > 0 и -1, если G < 0. Определим среднее состояние . Из симметричных соображений очевидно, что, когда E[M] = 0, элементы поровну распределены по состояниям +1 и -1.

Восприимчивость системы определяется как производная.

Видно, что восприимчивость системы определяет чувствительность среднего состояния на малое глобальное влияние. Восприимчивость имеет вторую интерпретацию – это изменение среднего на изменение случайных параметров e_i. Эта интерпретация означает следующее: если рассмотреть два элемента и один из них привести к определенному состоянию, тогда мера того, что и второй придет к тому же состоянию, будет пропорциональна c. По этой причине можно надеяться, что восприимчивость есть корректная мера способности элементов воздействовать согласованно. В этом случае два состояния, в которых может находиться отдельный элемент, дают глобальный механизм синхронизации через локальную имитацию, которая вызывает при определенных параметрах фазовый переход.

Таким образом, за основу берется поведение восприимчивости и предполагается, что а h(t) (скорость наступления аварии) зависит от c.

Модель сетевой топологии. При данном подходе рассматривается ансамбль элементов, связанных друг с другом в многоуровневую сеть. Структура имеет свойства, характерные для физических иерархических систем, и отдельные элементы, которые покрывают все уровни иерархии. Фактически в системе присутствует горизонтальная структура для взаимодействия индивидуальных элементов.

В данном подходе строится модель кристаллической решетки алмаза. Рассмотрим два связанных друг с другом элемента. Заменим эту пару на элементарную ячейку кристалла алмаза, где эти элементы займут противоположные точки на гранях алмаза. Кристалл алмаза содержит четыре связи. Каждую из них заменим опять на ячейку кристалла и будем продолжать эту операцию далее. После P итераций получим элементов в качестве вершин и 4 ^P связей между ними. Большинство элементов имеет только двух соседей, некоторые – 2 ^P, а другие – в промежутке между ними. Такая сетевая модель отражает более реалистичную картину связей в иерархических системах между элементами, чем на евклидовой плоскости (рис. 10).

Данная модель была решена в 1983 г. в работе Derrida [8]. Основные свойства ее решения: существует критическое значение P_C, причем при T < T_C восприимчивость конечна, при стремлении T к критическому значению она расходится. Существенное отличие данного подхода от рассмотренных выше – наличие комплексного критического индекса. Это приводит к качественно иному поведению перед фазовым переходом (аварией). Общее выражение для c следующее:,

где – вещественные числа. Видно, что степенной закон в данном случае «подправлен» осцилляциями, причем их период стремится к нулю при приближении к критической точке. Ускоряющиеся осцилляции называются лог-периодическими колебаниями, а – их лог-частота.

Вероятность наступления аварии (фазового перехода).

Таким образом, если в поведении какого-либо показателя (считываемой характеристики) видны лог-периодические осцилляции, то можно утверждать, что в этой системе зарождается кооперативное поведение отдельных ее элементов, приводящее к качественному изменению всей системы. Сигнатура h(t) была обнаружена в различных околофизических системах: подобное колебание демонстрирует цена на рынке перед большими падениями, та же сигнатура возникает в считываемом параметре концентрации изотопа хлора в родниках перед землетрясением. Последний пример показывает, что данная сигнатура может наблюдаться там, где свойства многоагентности не выражены четко либо не выражены вообще. Последние работы, изученные авторами, демонстрируют присутствие данной сигнатуры в том или ином виде во множестве приложений, начиная от теории турбулентного движения жидкостей и заканчивая физикой твердого тела области высокотемпературной сверхпроводимости (ВТСП) [5].

Изложение сущности подхода

Для многоэлементной системы идентификация сигнатуры h(t) означает, что некоторая часть элементов (агентов) в ней начинает свое воздействие в одном направлении, то есть элементарные векторы их сил однонаправленные. В этом случае физики говорят, что происходит самоорганизация в поведении агентов, и они начинают действовать кооперативно или сообща. Примечательным является тот факт, что нет никакой внешней силы, которая устанавливала бы множество элементарных агентов в однонаправленное состояние (система изолирована). Очевидно, существует некоторый механизм передачи информации между элементарными агентами, но интерпретировать и считывать элементарные взаимодействия для каждого отдельного агента не представляется возможным в силу их большого количества либо недоступности.

Если потенциал кооперативного действия подмножества объектов многоагентной системы окажется достаточным по величине, он может изменить направленность (вектор воздействия) ближайших к данному подмножеству элементов, которые до этого создавали однородное поле из-за хаотичности своего поведения. В этом случае произойдет так называемая передача информации через ближайших соседей. Последние элементы примкнут к кооперативному подмножеству, еще больше увеличив потенциал кооперативного подмножества. Распространение начнет происходить по цепочкам по множеству направлений. Там, где сила связи с ближайшим соседом сильная, скорость распространения (вовлечение новых элементов в кооперативное подмножество) будет продолжаться. Там, где сила связи мала либо отсутствует, цепочка распространения оборвется. Если оборвутся все цепочки по всем направлениям, распространение остановится и авария (кооперативный, мощный удар внутри технологической машины) не произойдет, если она не произошла до этого.

Комплексная модель диагностирования – интеграция модели Маркова
и модели обнаружения фазового перехода

Как уже было сказано выше, в конструируемой математической модели марковской модели отводится роль описания системы внутри интервалов времени, в которых система носит стационарный характер своего поведения, то есть внутри временных интервалов стационарности (множество М₁ в приведенном примере). В данное множество входят состояния: М₁ = {S₁, S₂, S₃}. К множеству М₂ относится одно состояние: М₂ = {S₄} (класс состояний аварийный).

Согласно графу состояний технологической системы (рис. 4), из М₂ система выходит с интенсивностью l₄₁ и сразу же после аварийного ремонта переходит в исправное состояние. Начальное значение для l₄₁ в модели зависит от примерной оценки времени, затраченного на проведение ремонта, включая время на заказ деталей с завода-изготовителя, доставку и прочее. Таким образом, можно с вероятностью, равной единице, утверждать, что в течение 3 недель технологический комплекс перейдет из аварийного состояния в исправное. Из

имеем .

В М₂ система может оказаться под управлением интенсивностей l₁₄, l₃₄, l₁₄ – интенсивность перехода из исправного состояния, l₃₄ – из неработоспособного. Необходимо проанализировать, должны ли отличаться данные интенсивности в зависимости от того, из какого состояния они направлены, или напротив, иметь одинаковые значения, исходя из того, что они ведут к одному и тому же аварийному состоянию. Если система оказалась в неработоспособном состоянии в контексте рассматриваемой далее системы – технологического комплекса измельчения, это означает, что пришло время текущего ремонта и в этом случае вероятность (соответственно и интенсивность) ничтожно мала, так как после планового ремонта комплекс переходит сразу в исправное состояние. Вероятность оказаться в аварийном состоянии, пройдя неработоспособное, имеет значения, гораздо большие нуля, только при возникновении цепочечного отказа. По результатам проводимых прогонов модели на исторических данных оборудования при условии l₁₄ = l ₃₄ имеется несколько завышенная оценка для P₄(t), что в условиях недопустимости аварийного состояния комплекса измельчения приемлемо.

Для вычисления интенсивности попадания в аварийное состояние необходимо в каждый момент времени после пуска комплекса знать мгновенную вероятность фазового перехода. До начала пуска эксперт (главный механик, технологи) устанавливает максимальное количество кооперативных ударов, которое может выдержать защитное покрытие барабана данного типа агрегата (МШР-3,6×4,0 или МШР-4,5×5,0) на данном рабочем интервале (пробеге) N(Ц_т), где Ц_т – межремонтный период (пробег, периодичность ремонта), измеряемый в часах. Если количество идентифицированных кооперативных ударов в мельнице на момент времени t равно , где t₀ – момент пуска комплекса, t – текущий момент времени, тогда вероятность фазового перехода в момент времени t.

Исходя из того, что D T = t – t₀, получим выражение для интенсивности фазового перехода для произвольного момента времени t:.

Начальные значения для интенсивностей устанавливаются исходя из статистических данных по частоте поломок и вероятности восстановления и равны соответственно: ; l₁₂ показывает, с какой интенсивностью в среднем происходят поломки, приводящие к неработоспособному состоянию, l₂₁ – вероятность восстановления системы приближается к 1 за час работы.

Таким образом, на основе рассчитываемых в реальном времени на основе модели идентификации сигнатур определяются новые значения матрицы интенсивностей переходов, и для каждого такого изменения пересчитываются новые будущие вероятности локально-стационарных состояний системы. Затем по вычисленным значениям вероятностей состояний, по рассматриваемому далее алгоритму выдаются рекомендации оптимального момента останова системы на техническое обслуживание.

Построение системы управления технологической безопасностью процессов измельчения

Рассмотрим контур управления процессом измельчения по оптимизации остановов машины на текущий ремонт (рис. 11).

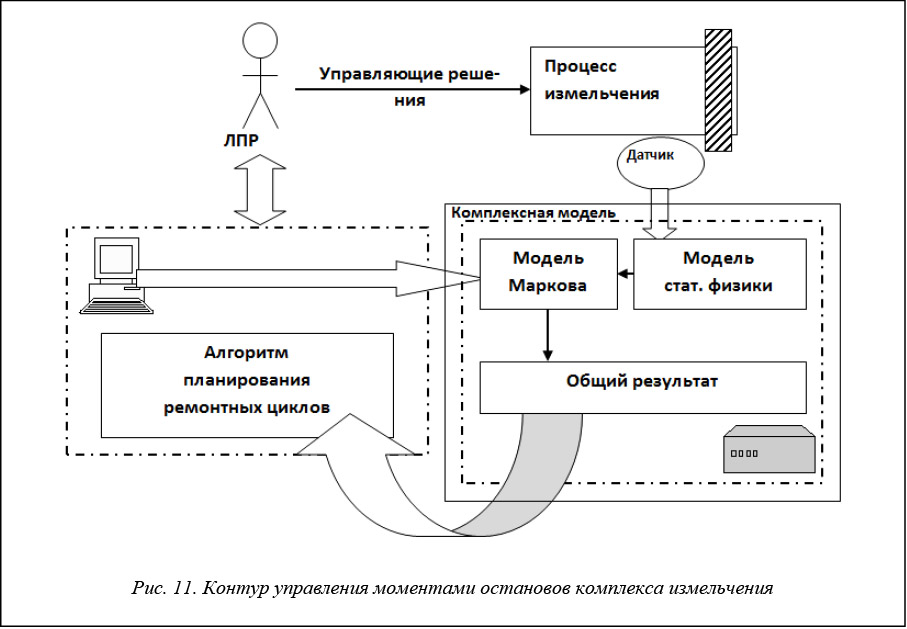
Диагностическая модель состояния комплекса измельчения (комплексная модель), образованная интегрированием модели Маркова и модели статистической физики по идентификации кооперативных ударов, может быть реализована на базе микроконтроллера. Последний имеет интерфейсный вход для поступающих данных от датчика вибрации области измельчения, вход для фиксаций сигналов о событиях по изменению состояния периферийного оборудования, поступающих от ЛПР (лицо, принимающее решение), и выход, на котором формируется вектор вероятностей состояний оборудования всего комплекса измельчения, представленного как общий результат комплексной модели диагностирования.

На базе персональной ЭВМ реализованы терминал по управлению микроконтроллером, отображению данных и запрограммированный алгоритм планирования оптимальных моментов остановов линий комплексов измельчения (машин) на проведение текущего ремонта. Анализируя рекомендации, выдаваемые системой, в виде рассчитываемых оптимальных моментов остановов, главный механик, технолог (эксперт) принимают решение остановить соответствующую линию на текущий ремонт либо продолжить эксплуатацию комплекса.

Последовательность расчетов, выполняемых в системе диагностики и управления по комплексной модели, рассмотрим в виде алгоритма (рис. 12), организованного посредством нескольких потоков, каждый из которых может быть создан асинхронно, по мере необходимости, в зависимости от результата расчета новых поступивших данных по шуму или действий оператора. Именно на базе такой схемы организован процесс расчета в комплексе программного обеспечения для персональной ЭВМ, рассматриваемый далее.

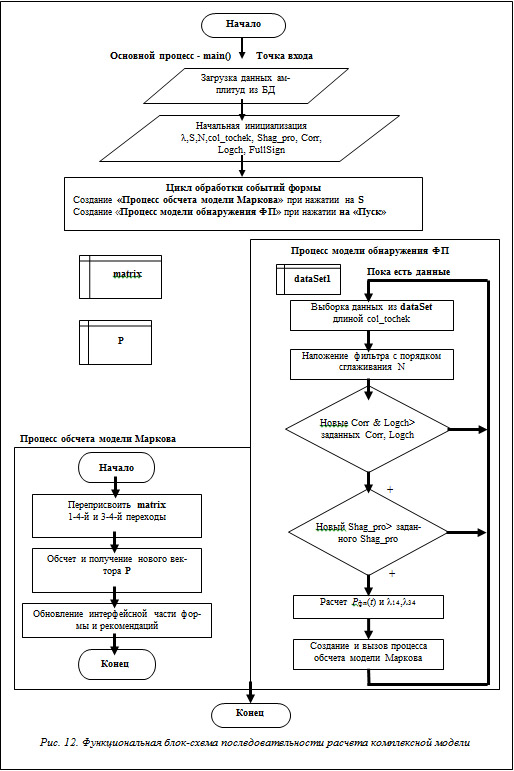
На этапе загрузки данных осуществляется инициализация переменных модели сохраненными прежде значениями, такими как матрица интенсивностей переходов λ на текущий момент времени для модели Маркова, различными параметрами моделирования (количество точек анализа (col_tochek) для метода статистической физики идентификации сигнатур, пороги идентификации – значение коэффициента корреляции и лог-частота (Corr, Logch)), указываются начальное состояние системы S на момент пуска, максимальное количество кооперативных ударов, которое может выдержать покрытие на данном пуске FullSign, и некоторые другие параметры (рис. 13).

Далее выполняется цикл опроса действий оператора ЭВМ (пользователя), который работает с данным программным комплексом. Если оператор хочет указать программной системе, что технологическая система (комплекс измельчения) перешла в новое состояние (например, из исправного в работоспособное), он щелкает мышью на соответствующее состояние и вводит причину перехода в появившемся окне (рис. 14).

Матрица интенсивностей изменяет свои значения во времени в зависимости от информирования программного средства пользователем посредством его интерфейса о возникающих на производстве инцидентах, посредством модуля «Процесс обсчета модели Маркова» обсчитываются новые значения вероятностей состояний. Таким образом, выполняется перерасчет предельных вероятностей для каждого из четырех состояний агрегата на момент работы (текущий момент времени). Результаты анализа выводятся в графическом и символьном видах.

Для каждого вновь поступившего значения сигнала датчика шума производится пересчет модели идентификации сигнатур посредством процесса «Процесс модели обнаружения ФП». Он создается постоянно от начала запуска и до момента останова. Если новые поступившие данные удовлетворяют заданным параметрам сигнатуры, удар считается идентифицированным и добавляется в общее количество, после чего на основе этого значения и максимально допустимого значения ударов рассчитываются P_фп(t) и λ₁₄, λ₃₄. Далее временно создается поток «Процесс обсчета модели Маркова» – так матрица интенсивностей обновляется и вероятности состояний системы пересчитываются вновь.

Разработанное программное обеспечение комплексной диагностической модели запускается для каждой линии измельчения отдельно. Вероятностные оценки эффективностных отказов (вероятность аварии), выдаваемые с каждой линии, поступают на вход алгоритма планирования оптимальных моментов остановов, который рассчитывает времена останова для каждого агрегата.

Поскольку состояния системы могут изменяться со временем случайным образом и система может подвергаться внешним случайным воздействиям, оценка качества функционирования также является случайным процессом. Наиболее часто в качестве показателей функционирования применяется математическое ожидание этих случайных величин. При непрерывной работе линии измельчения с течением времени по ряду причин происходит ухудшение условий работы, среди которых износ и повреждение как внутренней поверхности агрегата измельчения, так и периферийного оборудования (улитковые питатели и прочее). Это находит свое выражение в увеличении затрат, среди которых наибольший вес имеют затраты на замену износившихся футеровочных плит.

Будем понимать под C (Dt, S(t)) случайную величину удельных потерь на замену футеровочных плит от эффективностного отказа по истечении времени Dt после последнего ремонта этой линии.

Тогда

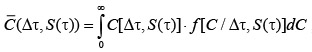, (1)

где – условный дифференциальный закон распределения вероятностей удельных потерь по футеровкам от эффективностных отказов линии. Для общих удельных затрат можно записать

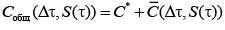. (2)

Есть математическое ожидание указанных удельных потерь в каждый момент времени t, характеризуемый величиной отрезка Dt и нагрузкой линии комплекса измельчения S(t).

В дальнейшем при разработке системы оптимального управления мельнично-флотационным отделением будет использоваться функция общих удельных затрат C _общ (Dt,S(t)). Данная функция была получена методом Брандона [10]. Исходные данные для определения функции общих удельных затрат получены на основе статистических данных по производству. По методу Брандона уравнение регрессии записывается в виде

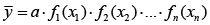. (3)

В нашем случае функция удельных затрат C_общ, у.е./ч, зависит от времени пробега комплекса измельчения (линии) с момента последнего текущего ремонта Dt и от нагрузки S(t) и имеет вид

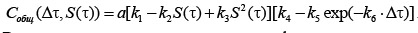. (4)

Результаты расчетов показывают, что функция удельных затрат имеет по нагрузке явно выраженный экстремум, а по продолжительности работы линии измельчения со времени последнего текущего ремонта затраты на футеровку увеличиваются, затем этот процесс устанавливается.

Основными управляющими воздействиями для мельнично-флотационного отделения можно назвать нагрузки на линии измельчения (комплексы) S_j (t), моменты остановок отдельных комплексов на ремонт t_jx. Поэтому задача оптимального управления системой параллельно работающих агрегатов измельчения состоит в минимизации основных технологических составляющих затрат на планируемом периоде при ограничениях на производительность отделения. В качестве таких составляющих были взяты затраты, имеющие наибольший вес в себестоимости продукции. В данном случае это затраты на футеровочные плиты. Ставится задача оценочного планирования нагрузок отдельных линий и продолжительности работы между остановками линий (комплексов измельчения) на ремонт.

В качестве критерия оптимума целесообразно использовать математическое ожидание потерь футеровок от эффективностных и функциональных отказов.

Общие потери отделения от эффективностных отказов за планируемый промежуток времени T:

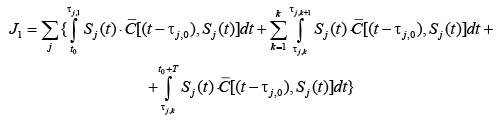(5)

где t _j,0 – момент времени, соответствующий последнему ремонту j-го комплекса до начала текущего интервала планирования; t₀– начало текущего интервала планирования; k_j – число остановок j-го агрегата на ремонт в течение интервала T.

С другой стороны, потери, возникающие в результате функциональных отказов комплексов измельчения на отрезке времени T, определяются как сумма затрат на проведение всех ремонтных работ за это время:

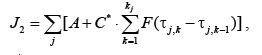, (6)

где

A– минимально возможные затраты на проведение ремонта комплекса (когда он находится в хорошем состоянии);

A+A ^*– полные затраты на ремонт при возникновении функционального отказа на линии;

F– интегральный закон распределения вероятностей возникновения функционального отказа по истечении времени после последнего ремонта агрегата.

Таким образом, необходимо определить такую совокупность управляющих воздействий S_j(t) и t_jx (для всех j) на протяжении планируемого периода Т, чтобы

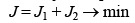 (7)

и соблюдались ограничения на выработку продукта (8), нагрузки (9) и несовпадение моментов останова различных линий на ремонт (10):

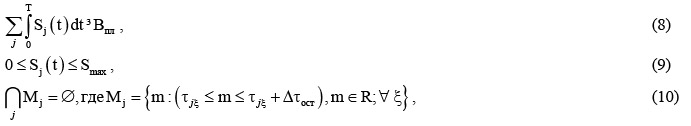
где B_пл – планируемая выработка за время; S_max – предельно возможная нагрузка на линию; Dt_ост – средняя продолжительность ремонта линии.

Упрощенная структурная схема алгоритма оптимизации приведена на рисунке 15.

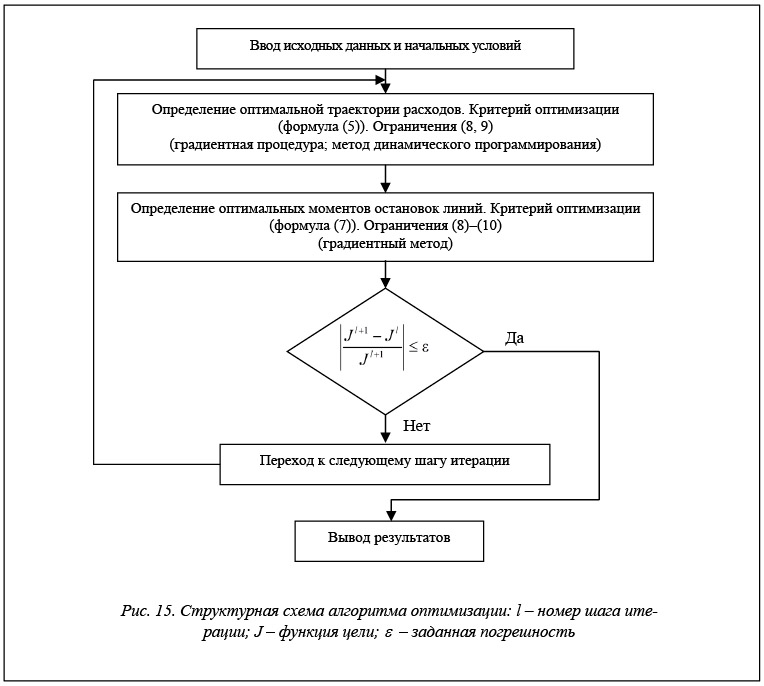
Основными этапами являются определение оптимальной траектории усредненных нагрузок на комплексы и расчет оптимальной продолжительности работы между текущими ремонтами.

В заключение эксперт (обслуживающий персонал) на основании рассчитанных значений модели, а именно знания вероятности ближайших состояний и количества уже произошедших кооперативных ударов, а также на основе рекомендаций, выдаваемых алгоритмом планирования текущих остановов, принимает решения о продолжении эксплуатации либо останове того или иного комплекса измельчения на текущий ремонт.

Литература

1. Перов В.А., Андреев Е.Е., Биленко Л.Ф. Дробление, измельчение и грохочение полезных ископаемых. М.: Недра, 1990. 300 с.

2. Охота С.В., Кулаков А.Г., Пророков А.Е. Оптимальное планирование межремонтных циклов агрегатов измельчения // Прикладные проблемы управления макросистемами: матер. VII Всерос. школы-семинара, 31 марта–4 апреля 2008, г. Апатиты. Апатиты: Изд-во КНЦ РАН, 2008. С. 74–78.

3. Палюх Б.В. Приложения метода разделения состояний к управлению технологической безопасностью на основе индекса безопасности. Тверь: Изд-во ТГТУ, 2009. 368 с.

4. Новые технологии диагностики состояний и управления безопасностью промышленных процессов. Тверь: Изд-во ТвГТУ, 2012. 64 с.

5. Кузнецов С.П. Динамический хаос. М.: Физмалит, 2000. С. 294.

6. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения. М.: Высшая школа, 2000. 383 c.

7. Булинский А.В., Ширяев А.Н. Теория случайных процессов. М.: Физматлит, 2005. 408 c.

8. Johansen A., Ledoit O. and Sornette D. Crashes as critical points, International Journal of Theoretical and Applied Finance. 2000, no. 3 (2), pp. 219–255.

9. Derrida B., De Seze L., Itzykson C. 1983. Fractal structure of zeros in hierarchical models. Journal of Statistical Physics, 1983, no. 33, p. 559.

10. Чавкин А.М. Методы и модели рационального управления в рыночной экономике. М.: Финансы и статистика, 2001. 320 с.