Т-система представляет собой концепцию автоматического динамического распараллеливания, в которой сочетаются наиболее удачные черты функционального программирования, dataflow-систем и традиционных языков и методов программирования [1, 2].
Современная реализация концепции Т-системы (OpenTS [3]) обладает открытой и масштабируемой архитектурой, легко адаптируемой к стремительно меняющимся аппаратным платформам современных суперкомпьютеров. Поддерживаемый системой OpenTS входной язык программирования Т++ является синтаксически и семантически гладким расширением языка программирования Си++, а среда исполнения Т-приложений представляет собой надстройку (Т-суперструктуру) над стандартной последовательной средой программирования.
Для системы OpenTS разработаны решения, с помощью которых были реализованы основные положения адаптивного отказоустойчивого алгоритма в системе активного хранения и обработки данных. Алгоритм позволяет системе принимать решения о необходимости резервного копирования внешних данных большого размера в среде с заданной вероятностью отказа.
Работа Т-системы в отказоустойчивом режиме с одним «безотказным» узлом
Наиболее общепринятым способом обеспечения отказоустойчивости приложения является создание контрольных точек, то есть записей на внешнем хранилище состояний программы, значений ключевых переменных. При сбое системы программу запускают не с начала, а с последней контрольной точки. Создание контрольных точек для программы требует от программиста дополнительных усилий: в определенных местах исходного текста нужно расставлять вызовы подпрограмм сохранения контрольных точек.
В системе OpenTS применяется другой подход [4] к обеспечению отказоустойчивости параллельных приложений, который состоит в том, что на кластере выделяется узел, который объявляется «безотказным», и с помощью него осуществляется обеспечение отказоустойчивости параллельного счета. В этом случае заботу об обеспечении отказоустойчивости берет на себя не программист, а Т-система, программист при написании программы лишь должен следовать нескольким простым правилам. Т-система в отказоустойчивом режиме сама адаптируется к сбоям, автоматически восстанавливая отказавшие задачи.
Отказоустойчивость приложения проверяется следующим образом. Выполняется запуск параллельного приложения на нескольких узлах вычислительного кластера с числом процессов на узле, равным числу процессорных ядер. Выполняется проверочный останов процесса (например командой kill) на одном из счетных узлов. Планировщик Т-системы, работающий на «безотказном» узле, обнаруживает факт останова процесса, находит идентификатор Т-задачи, которую выполнял этот процесс, и перенаправляет задачу другому процессу на одном из доступных узлов. Таким образом, при отказе любого узла кластера, кроме «безотказного», приложение переназначает на другие узлы задачи, работавшие на отказавшем узле.
Чтобы Т-приложение имело свойство отказоустойчивости, программист должен соблюдать следующие правила.
1. Вместо mpirun/mpiexec для запуска приложений использовать командный файл trun.sh.
Т-приложение запускается с помощью mpirun/mpiexec или через вызов специального командного файла trun.sh (см. Приложение A). В отказоустойчивом режиме Т-приложение следует запускать только с помощью командного файла trun.sh. При подготовке командного файла к работе программисту следует в первой строке файла в переменной окружения «path» указать полный путь к каталогу с приложением и создать файл конфигурации trun.cfg, каждая строка которого содержит IP-адрес узла кластера. Первый IP-адрес в файле конфигурации – это адрес «безотказного» узла кластера. Запуск приложения осуществляется на узле, который следует первым в файле конфигурации. Вызывается сценарий trun.sh, которому в качестве аргументов командной строки передаются путь к приложению и параметры командной строки. Результат работы приложения выводится в журнал регистрации событий (для каждого узла свой журнал).
2. Вместо стандартного вывода (stdout) использовать стандартный вывод ошибок (stderr).
Например, отказоустойчивая версия задачи Фибоначчи [5] отличается от обычной только тем, что вывод результата производится на системный вывод stderr (см. Приложение B).
3. Избегать использования выражений, содержащих ранг.
Поскольку при отказе задачи происходит ее перезапуск на другом узле и ей будет назначен другой ранг, результат задачи не должен зависеть от ее ранга. Поэтому в приложении не рекомендуется использовать выражения, содержащие ts::myRank. Если все же есть необходимость в использовании таких выражений, следует предусмотреть корректное восстановление таких выражений при перезапуске задачи с новым рангом. Например, это можно сделать с помощью внешнего хранилища (см. Приложение C).
4. При необходимости осуществлять резервное копирование входных файлов.
Если приложение имеет входные файлы, расположенные на внешнем хранилище, которое может отказать, следует сделать копии этих файлов на резервном хранилище. При открытии файла, если он не обнаружен, приложение должно попытаться открыть резервную копию файла.
Планировщики системы OpenTS
Планировщик системы OpenTS принимает решения о порядке исполнения задач. Его назначение в том, чтобы путем пересылок Т-задач между узлами кластера свести общее время исполнения программы к минимуму. Это означает, что в каждый момент времени каждый узел кластера должен быть занят какой-либо работой. Узел простаивает, если его очередь пренатальных задач (ptq) пуста, а все исполняемые задачи находятся в ожидании ресурсов. Таким образом, главная задача планировщика – обеспечить наличие задач в очереди на каждом узле.
Пусть имеется высокопроизводительная вычислительная система, состоящая из N узлов. На каждом узле выполняется множество задач. Задачи делятся на пренатальные и исполняемые (непренатальные). Пренатальные задачи могут перемещаться между узлами кластера, исполняемые не могут. Исполняемые задачи, в свою очередь, делятся на ожидающие неготового значения и готовые к исполнению (ожидающие процессорного времени).
Планировщик может предпринимать следующие действия:
– переслать одну или несколько пренатальных задач на другие узлы;
– возобновить одну из исполняемых задач;
– запустить одну из пренатальных задач, тем самым переводя ее в категорию исполняемых.
При сборке по умолчанию Т-приложение будет использовать основной планировщик, но с указанием параметра сборки «–sched=gs» этот планировщик будет заменен на метапланировщик [6] для работы в условиях распределенной сети вычислителей. Его можно использовать в том случае, когда обмен информацией между узлами происходит с задержкой. Метапланировщик обеспечивает пересылку задач с узла на узел задолго до того, как на одном из них закончится работа. Таким образом, вероятность простоя узла уменьшается.
Эффективное планирование работы Т-системы при заданном начальном количестве
параллельных задач (задача оптимизации с закрепленным концом)
Часто в приложениях возникают задачи типа «запустить максимально возможное количество параллельных подзадач». К таковой, например, относится задача распараллеливания оператора цикла «for». При таком распараллеливании область значений переменной индекса оператора цикла разбивается на N областей и запускаются N параллельных подзадач, в каждой из которых переменная индекса оператора цикла пробегает по одной из этих областей. При этом подзадачи распределяются равномерно по всем рангам, которые предоставлены Т-системе средой MPI. Пример того, как это можно реализовать в
Т-системе, показан в [5], приложение F. Естественно, планировщик при этом не отключается, а продолжает эффективно распределять ресурсы при выполнении приложения.
Задача обеспечения эффективности и отказоустойчивости приложений
с входными файлами большого объема
При наличии у задач входных файлов большого объема при планировании задачи следует принять (адаптивное) решение, сохранять копии этих файлов в резервном хранилище или нет, поскольку копирование таких файлов может занять продолжительное время. Пока для определенности мы рассматриваем следующую задачу: приложение порождает N независимых счетных задач, причем для каждой задачи свои входные данные.
Сначала оценим время выполнения задачи t. Если оценка времени превосходит некоторый порог Ts, будет сохранена копия входного файла на резервном хранилище, в противном случае копия не сохраняется.
Пусть t зависит от размера входного файла Vi и N, i=1, …, N.
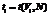 .
.
Например, если ti зависит квадратично от Vi (квадратичная сложность алгоритма), то
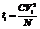
и решающее правило будет выглядеть следующим образом.
При выполнении 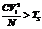 будем сохранять копию входного файла на резервном хранилище, в противном случае копия не сохраняется.
будем сохранять копию входного файла на резервном хранилище, в противном случае копия не сохраняется.
Если вероятность отказа подчиняется распределению Пуассона, то вероятность того, что за время t произойдет n отказов, равна
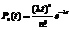 ,
,
a вероятность безотказной работы за время t равна
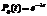 .
.
Вычислим вероятность отказа за время Тs:
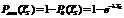 .
.
Использование «облачного» внешнего хранилища
При использовании внутри Т-функции директивы tct(cloud) ее входные параметры при ее вызове сохранятся во внешнем удаленном хранилище [7] и будут там храниться до тех пор, пока не завершится порожденная при этом вызове задача. При отказе задачи данные будут отправлены во внешнее хранилище и системный программист сможет восстановить задачу, запустив Т-функцию с сохраненными параметрами.
Таким образом, в статье описаны две модели обеспечения отказоустойчивости в Т-системе с открытой архитектурой: отказоустойчивый режим с одним «безотказным» узлом мультипроцессорной вычислительной системы и модель с использованием «облачного» внешнего хранилища, в которой значения параметров Т-функций сохраняются в базе данных, что позволяет перезапустить отказавшие задачи. Рассмотрена задача обеспечения эффективности и отказоустойчивости приложений с входными файлами большого размера. Приведен пример отказоустойчивой версии программы умножения матриц.
Работы, положенные в основу данной статьи, были выполнены в рамках Программы фундаментальных исследований Президиума РАН № 14 «Проблемы создания национальной научной распределенной информационно-вычислительной среды на основе GRID-технологий, облачных вычислений и современных телекоммуникационных сетей».
Литература
1. Абрамов С.М., Васенин В.А., Мамчиц Е.Е., Роганов В.А., Слепухин А.Ф. Динамическое распараллеливание программ на базе параллельной редукции графов. Архитектура программного обеспечения новой версии Т-системы // Науч. сессия МИФИ-2001. Т. 2. Информатика и процессы управления. Информационные технологии. Сетевые технологии. Параллельные вычислительные технологии: сб. науч. тр. М., 2001. С. 34–235.
2. Абрамов С.М., Кузнецов А.А., Роганов В.А. Кроссплатформенная версия Т-системы с открытой архитектурой // Параллельные вычислительные технологии: тр. Междунар. науч. конф. Т. 1 (29 января–2 февраля 2007 г., г. Челябинск). Челябинск: Изд-во ЮУрГУ. С. 115–121.
3. Абрамов С.М., Кузнецов А.А., Роганов В.А. Кроссплатформенная версия T-системы с открытой архитектурой // Вычислительные методы и программирование. 2007. Т. 8. № 1. Раздел 2. С. 175–180; URL: http://num-meth.srcc.msu.su/ (дата обращения: 10.02.2014).
4. Кузнецов А.А., Роганов В.А. Экспериментальная реализация отказоустойчивой версии системы OPENTS для платформы WINDOWS CCS // Суперкомпьютерные системы и их применение: тр. II Междунар. науч. конф. (27–29 октября 2008 г., г. Минск). Минск: ОИПИ НАН Беларуси, 2008. С. 65–70.
5. OpenTS. Руководство программиста. URL: http://www.opents.net/index.php/ru/ruk-progr (дата обращения: 10.02.2014).
6. Степанов Е.А. Планирование в OpenTS – системе автоматического динамического распараллеливания // Информационные технологии и программирование: межвуз. сб. статей; [под ред. В.А. Васенина, Д.Л. Ревизникова, Е.А. Роганова]. М.: Изд-во МГИУ, 2005. Вып. 2 (14). С. 31–42.
7. Кузнецов А.А., Роганов В.А. Поддержка отказоустойчивых хранилищ данных в системе OpenTS // Программные системы: теория и приложения: электрон. науч. журн. 2011. № 3 (7). С. 53–60; URL: http://psta.psiras.ru/read/psta2011_3_53-60.pdf (дата обращения: 10.02.2014).
Приложение A. Командный файл для вызова Т-приложения без mpirun/mpiexec
# set your path here
path="/home/user/msort"
cd $path
configfile="trun.cfg"
master="127.0.0.1"
port="8600"
b=0;
ETH0=$(/sbin/ifconfig eth0 | sed -n "2s/[^:]*:[ \t]*\([^ ]*\) .*/\1/p")
count=`awk '{if (!index($1,"#")) nmatches++} END { print nmatches}' $configfile`
for i in `awk '{ if (!index($1,"#")) print $1 }' $configfile`
do
if [ $b = 0 ] ; then
node=$master
fi
comm="export DMPI_MASTER=$node;export DMPI_MASTER_PORT=$port; export DMPI=\"chrys $count\"; cd $path ; $@ > $i.log 2>&1 "
if [ $i != $ETH0 ] ; then
eval /usr/bin/ssh $i "\"${comm//\"/\\\"}\"" &
else
comm2=$comm
fi
if [ $b = 0 ] ; then
node=$i
b=1
fi
done
sleep 1
eval "$comm2"
Приложение B. Отказоустойчивая версия задачи Фибоначчи
#include <stdio.h>
#include <stdlib.h>
tfun int fib (int n) {
return n < 2 ? n : fib(n-1) + fib(n-2);
}
tfun int main (int argc, char *argv[]) {
if (argc != 2) { printf("Usage: fib <n>\n"); return 1; }
int n = atoi(argv[1]);
fprintf(stderr,"fib(%d) = %d\n", n, (int)fib(n));
return 0;
}
Приложение C. Отказоустойчивая версия задачи умножения матриц (демонстрационный пример)
#include <stdio.h>
#include <cstdio>
#include <stdexcept>
#include "array.h"
#define DELAY 30
#define SAVED_RANKS_FILENAME "rank.bin"
struct RankInfo {
short n;
short rank;
};
typedef Array<float,2> matrix;
int status;
#if !defined(TEST1) && !defined(TEST2)
#define TEST1
#endif
#ifdef TEST1
#define N 1000
#endif
#ifdef TEST2
#define N 6
float a[6][6] =
{{1,1,1,1,1,1},
{1,2,3,4,5,6},
{1,3,6,10,15,21},
{1,4,10,20,35,56},
{1,5,15,35,70,126},
{1,6,21,56,126,252}};
float b[6][6] =
{{6,-15,20,-15,6,-1},
{-15,55,-85,69,-29,5},
{20,-85,146,-127,56,-10},
{-15,69,-127,117,-54,10},
{6,-29,56,-54,26,-5},
{-1,5,-10,10,-5,1}};
float c[N][N];
#endif
#ifndef TEST2
float a[N][N];
float b[N][N];
float c[N][N];
#endif
#ifdef TEST1
int init() {
for ( int i=0; i<N; i++)
for (int j=0; j<N; j++) {
a[i][j] = rand() % 9 - 4;
b[i][j] = rand() % 9 - 4;
}
return 0;
}
#endif
#ifdef TEST2
int init() {
return 0;
}
#endif
int saveRank(int n, int rank) {
FILE *file;
struct RankInfo buf;
buf.n = n;
buf.rank = rank;
file = fopen(SAVED_RANKS_FILENAME,"a");
fwrite(&buf, sizeof(RankInfo), 1, file);
fflush(file);
fclose(file);
return 0;
}
int getFileSize() {
struct stat filestatus;
int rc = stat( SAVED_RANKS_FILENAME, &filestatus );
if (rc != 0)
throw std::runtime_error("Can not find saved ranks file.");
return filestatus.st_size;
}
int getSavedRank(int n) {
FILE *file;
uint size;
int i=0;
while ((size = getFileSize()) != ts::realsuperSize*sizeof(RankInfo)) {
usleep(100*1000);
i++;
if(i > DELAY) {
throw std::runtime_error("getSavedRank is delayed\n");
}
}
struct RankInfo buf;
if (i <= DELAY) {
file = fopen(SAVED_RANKS_FILENAME,"r");
while (!feof(file)) {
fread(&buf, sizeof(RankInfo), 1, file);
if (buf.n == n) {
fclose(file);
return buf.rank;
}
}
fclose(file);
}
return -1;
}
tfun int mult( int n, matrix tout tarr, int rank) {
int nproc = ts::realsuperSize;
int imin = N*rank/nproc;
int imax = N*(rank+1)/nproc;
tval matrix ta;
matrix &arr = (matrix&) ta;
arr.Resize(imax-imin,N);
for (int i=imin; i<imax; i++) {
for (int j=0; j<N; j++) {
arr[i-imin][j] = 0;
for (int k=0; k<N; k++)
arr[i-imin][j] += a[i][k] * b[k][j];
}
}
tarr = (matrix&)ta;
status = 3; // Application is finished
return 0;
}
tfun int g(int n, int tout rank, matrix tout tarr) {
fprintf(stderr, "g rank%d n=%d\n", ts::myRank, n);
if (status == 0) {
init();
saveRank(n, ts::myRank);
rank = ts::myRank;
status = 1; // Initialization is done
}
rank = getSavedRank(n);
if (rank == -1) { // rejected task
tval matrix ta;
matrix &arr = (matrix&) ta;
arr.Resize(1,1);
tarr = (matrix&)ta;
return 1;
}
status = 2; // Application is started
(int)mult(n, tarr, rank);
return 0;
}
void print(float c[N][N]) {
for (int i=0; i<N; i++) {
for (int j=0; j<N; j++)
printf("%.0f\t",c[i][j]);
printf("\n");
}
}
tfun int f(int n) {
int res;
tval int rank;
tval matrix tarr;
if (n < 1)
res = g(n, rank, tarr);
else
res = f(n-1)+g(n, rank, tarr);
if (rank == -1)
return res;
matrix &arr = (matrix&) tarr;
int imin = N*rank/ts::realsuperSize;
int imax = N*(rank+1)/ts::realsuperSize;
for (int i=imin; i < imax; i++)
for (int j=0; j<N; j++)
c[i][j] = arr[i-imin][j];
return res;
}
tfun int main(int argc, char* argv[]) {
std::remove(SAVED_RANKS_FILENAME);
int res = (int)f(ts::realsuperSize);
printf("res=%d\n", res);
if (res > 1)
throw std::runtime_error("Can not allocate ranks. Please try again.");
print(c);
return 0;
}
Комментарии