Классификация методов представления иерархий в РСУБД

На сегодняшний день реляционный сервер является неотъемлемым компонентом современной информационной системы. Практически все корпоративные приложения в различных предметных областях используют реляционные серверы для хранения и оперирования большими объемами данных. В свою очередь, реляционная модель, разработанная Коддом [1–3], позволяет отображать большинство структур данных, поддерживать их целостность и актуальность. Однако реляционные таблицы являются «плоскими» структурами, и это осложняет представление сложно структурированных данных, таких как деревья и графы.

Задача представления иерархий в реляционном сервере является достаточно важной и освещается в различной литературе [1–4, 6–13]. Метод хранения деревьев был даже описан в стандарте SQL. Однако, несмотря на большое количество исследований по этой теме [4–5, 7–9] и аналитические работы по сопоставлению методов отображения иерархии в реляционные таблицы [1–4, 6–13], остается ряд вопросов.

В частности, исследователи используют различные способы классификации рассматриваемых ими методов, зачастую относя один и тот же подход к различным классификационным группам [4, 5, 7, 8], что вносит путаницу в изучение вопроса. Поэтому актуальной задачей является разработка единой классификации для известных (или, по крайней мере, наиболее распространенных) способов записи деревьев в реляционный сервер. Рассмотрим основные подходы к взаимному отображению данных.

Исторически первым методом является использование классической модели с рекурсивным указателем (рис. 1). По сути это помещение матрицы смежности в таблицу, то есть один столбец – родительский узел, а другой столбец в той же самой строке – дочерний узел (пара представляет собой дугу в графе). Данный подход был предложен еще Е.Ф. Коддом и реализован в учебной базе ORACLE "Scott/Tiger", которая поставлялась с этим продуктом [3].

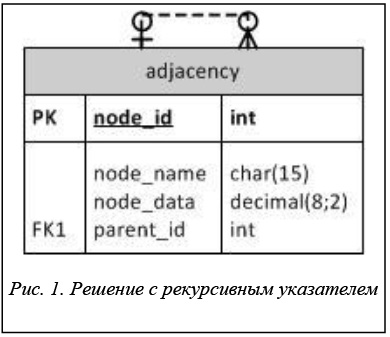
К недостаткам рекурсивного подхода к получению данных из модели списков смежности являются медленность и неэффективность. К тому же, помимо того, что таблица является денормализованной и значения столбцов node_id и parent_id в нормализованной таблице должны располагаться в одном столбце, модель списка смежных вершин не моделирует подчинение [4].

Наиболее распространенным усовершенствованием основной модели является отделение структуры от данных, как показано на рисунке 2. Одна таблица содержит только данные, а структура выносится в дополнительную таблицу nodes_chart, имеющую два отношения «один-ко-многим»
с таблицей данных nodes_list. Таким образом, node_id и parent_id – внешние ключи, ссылающиеся на таблицу nodes_list.

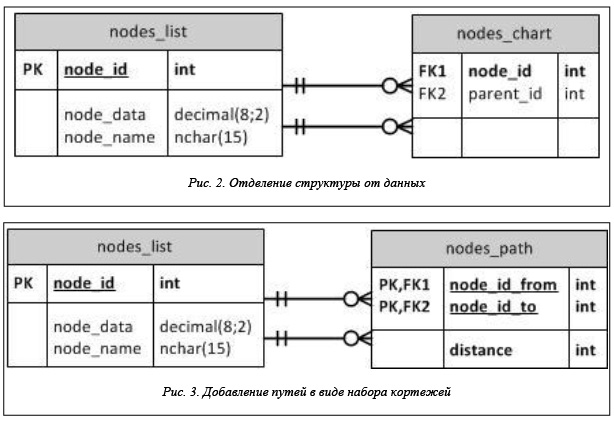
Назовем этот подход моделью с рекурсивным указателем и вспомогательной таблицей. Однако в ряде задач классическая модель рекурсивного указателя требует для поиска данных объемных и сложных запросов с самообъединениями и временными таблицами [4]. Отделение структуры от данных не дает особых преимуществ. Требуется новая, более сложная модель хранения, и таковой является модель с хранением пар предок–потомок с добавлением глубины. В этом случае требуются две таблицы (рис. 3).

Здесь для каждого родителя хранятся не только его непосредственные дети, но и все его потомки с соответствующей глубиной потомка для каждой пары предок–потомок.

Другая из усовершенствованных моделей списка смежных вершин также описывается двумя таблицами [10–12]. Есть базовая таблица, которая реализует иерархические отношения родитель–ребенок, и есть отдельная таблица, содержащая все отношения потомок–наследник, как и в предыдущем случае. Схемы таблиц приведены на рисунке 4.

Таким образом, таблица Tree получается из таблицы nodes_path удалением поля depth, а таблица adjacency является классической моделью рекурсивного указателя. Назовем ее моделью с рекурсивным указателем и хранением пар предок–потомок. В [10] предлагается некоторая математическая формализация, ориентированная на данную модель.

В [12, 13] предлагается добавлять в дополнительную таблицу поле, представляющее расстояние между узлами (то есть использовать таблицу nodes_path). Схема хранения принимает вид, представленный на рисунке 5.

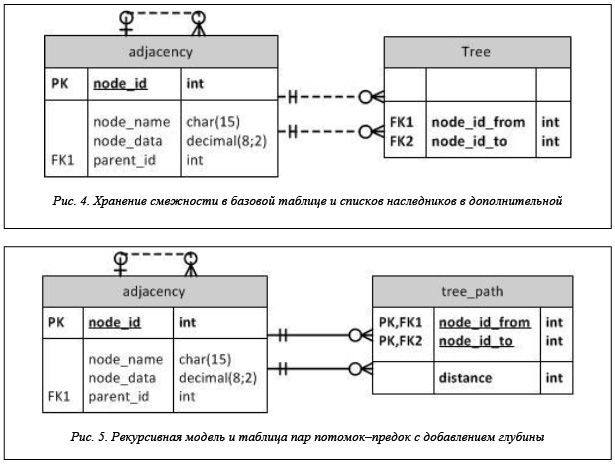
Этот подход можно охарактеризовать как модель с рекурсивным указателем и хранением пар предок–потомок с добавлением глубины.

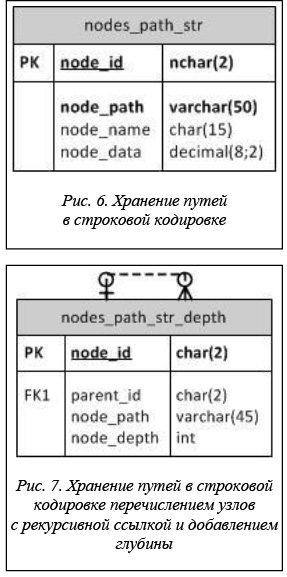
Еще одним подходом является использование моделей с хранением пути в строковом виде (рис. 6). Здесь можно выделить два основных подхода: модель хранения путей в строковой кодировке перечислением узлов [8] и модель хранения путей в строковой кодировке вложенными множествами (или вложенными списками) [7]. Здесь и далее последний случай будем называть моделью хранения путей в строковой кодировке вложенными списками, чтобы не путать с рассмотренной далее моделью вложенных множеств [8]. Также существует модификация этого подхода (для обоих вариантов) с хранением рекурсивного указателя.

Назовем эти варианты моделью с рекурсивным указателем и хранением путей в строковой кодировке перечислением узлов и моделью с рекурсивным указателем и хранением путей в строковой кодировке вложенными списками.

Рассматривается также расширение этих моделей с добавлением глубины (рис. 7) [9].

Также необходимо отметить принципиально другой подход – множественную модель деревьев, предложенную Joe Celko [8]. является модель с хранением пар предок–потомок с добавлением глубины. В этом случае требуются две таблицы (рис. 3). В работе [7] она обозначена как модель «маршрут обхода».

Метод отображения использует результат обхода дерева в глубину, присваивая каждому узлу два числовых значения: одно при «входе» в узел в процессе обхода, другое при «выходе» из него. Нумерация начинается с корня дерева.

Таким образом, оперируя полученными значениями, можно представить иерархию как набор вложенных друг в друга вершин, взаимное вхождение которых определяется вложенностью их номеров (рис. 8).

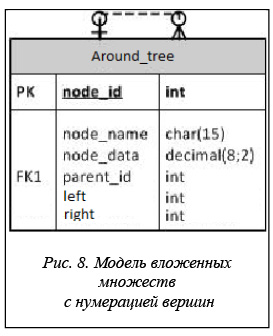
Исходя из принципиального подхода к представлению дерева, а также из возможности существования других способов присвоения вершинам вложенных или непересекающихся диапазонов номеров, назовем эту модель моделью вложенных множеств с нумерацией вершин. Стоит также отметить, что в описании и работе с моделью также используется рекурсивная ссылка, так что, наиболее правильным было бы название модель с рекурсивным указателем и вложенными множествами с нумерацией вершин.

Подобное обилие подходов и вариаций на их базе требует упорядочения и систематизации для общего подхода к именованию и описанию моделей. Проанализировав все рассмотренные способы, выделим следующие классификационные признаки.

1. Подход к представлению дерева.

В данном аспекте можно выделить два подхода. Все рассмотренные схемы либо основаны на рекурсивном представлении дерева, либо используют множественную модель деревьев. Ко второму случаю, в частности, можно отнести модель вложенных множеств с нумерацией вершин (хотя в ней и присутствует элемент рекурсивного представления) и модель с хранением путей в строковой кодировке вложенными списками.

2. Используемый метод хранения связей между вершинами.

Эта категория рассматривает хранение непосредственной связи между вершинами. В большинстве случаев методом хранения является рекурсивная ссылка. Избежать ее внедрения в модель позволяют метод вложенных множеств Joe Celko и хранение путей в строковой кодировке. Однако этот критерий очень близок к механизмам хранения и пересекается с ними. Будем считать, что основной метод хранения представлен одним из механизмов, рассмотренных далее.

3. Механизмы хранения данных.

Механизмы хранения данных – это методы представления тех или иных сведений об иерархии, повышающие эффективность работы с моделью на том или ином классе задач и в то же время увеличивающие избыточность данных, а в ряде случаев имеющие некоторые другие недостатки. В качестве таких механизмов можно назвать следующие:

– рекурсивная ссылка;

– хранение пар предок–потомок;

– строковое хранение путей;

– хранение глубины.

Так как в ряде подходов, не основанных на рекурсивном представлении дерева, может использоваться рекурсивная ссылка для упрощения работы с моделью, необходимо вынести ее в дополнительные механизмы, которые могут наличествовать или отсутствовать в ряде отображений. Для рекурсивного подхода этот дополнительный механизм будем считать обязательным. Также включим в этот список хранение путей, так как оно может использоваться дополнительно при рекурсивном подходе. Необходимо
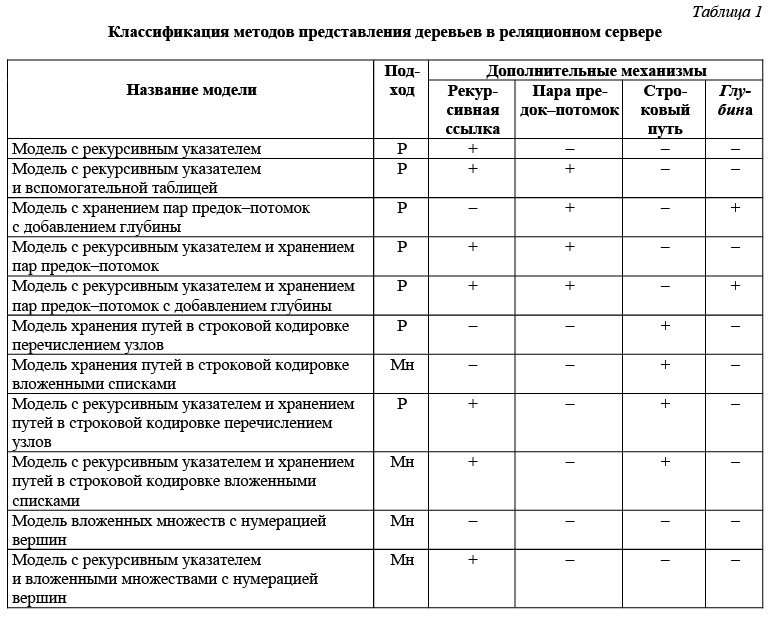
отметить, что первые три механизма – рекурсивная ссылка, хранение пар предок–потомок и строковое хранение путей – могут выступать как самостоятельные механизмы хранения, а глубина – только как дополнительный к строковому представлению или парам предок–потомок. Таким образом, можно выделить подход к классификации методов представления деревьев в реляционном сервере, представленный в таблице 1, где Р – рекурсивный подход к представлению иерархии; Мн – множественный подход к представлению иерархии.

Проанализировав приведенную в таблице 1 классификацию, отметим, что она позволяет охватить описанные на сегодняшний день модели и отразить их уникальность и многообразие. Также она позволяет формирование и оценку моделей, еще не описанных в источниках, но предполагаемых по сочетанию признаков.

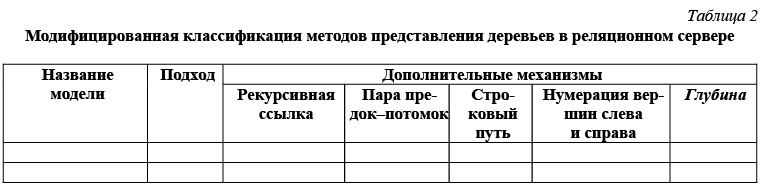
С другой стороны, у данной классификационной схемы есть один недостаток: модель вложенных множеств с нумерацией вершин не относится ни к одному механизму хранения, что позволяет установить подход, не используемый в ней, но ничего не говорит о реальном хранении данных. Очевидно, предложенный Joe Celko метод требует введения отдельного механизма хранения, расширяющего типовой набор и применимого вместе с уже существующими (что демонстрирует модель с рекурсивным указателем и вложенными множествами с нумерацией вершин). Вариант заголовка классификационной схемы с учетом этого факта приведен в таблице 2.

Используя такой подход, можно предложить унифицированный способ именования различных способов хранения сложных структур данных (в частности, иерархий) в реляционной БД. В качестве базового названия модели можно применить подход к отображению, а для уточнения привести используемые механизмы. Например, рекурсивный метод с парами предок–потомок и добавлением глубины или множественный метод с рекурсивной ссылкой и хранением путей в строковой кодировке. Возможно, при разработке новых схем отображения классификация будет нуждаться в уточнении, однако на сегодняшний день некоторая громоздкость наименования компенсируется однозначностью и отображением всех используемых в реальной схеме механизмов.

Таким образом, предложены классификация моделей представления деревьев в реляционном сервере, содержащая расширяемые средства описания существующих моделей, и принцип единого именования способов отображения иерархии для унификации терминологии в этой области исследований.

Литература

Codd E.F. Extending the Relational Database Model to Capture More Meaning. IBM Research Report RJ2599 1979. Republ. in ACM Transactions on Database Systems, 1979, no. 4, vol. 4, pp. 46–92.
Codd E.F. The Relational Model for Database Management. Version 2. Addison-Wesley Publ., 1990, 243 p.
Codd E.F. Data Models in Database Management. Proc. Workshop in Data Abstraction, Databases, and Conceptual Modelling / (M.L. Brodie and S.N. Zilles, eds.), Pingree Park, Colo. (June 1980): ACM SIGART Newsletter, 1981, no. 74; ACM SIGMOD Record 1981, no. 11, vol. 2; ACM SIGPLAN Notices, 1981, no. 16, vol. 1.
Полтавцева М.А. Хранение сложных структур данных в реляционной базе данных: монография. Тверь, 2013. 172 с.
Маликов А.В. Ориентированные графы в реляционных базах данных // Докл. Томского гос. ун-та систем управления и радиоэлектроники. 2008. № 2 (18). Ч. 2. С. 57–63.
Полтавцева М.А. Программные реализации схем представления структурированных данных в реляционной базе данных // Программные продукты и системы. 2008. № 1. С. 20–22.
Тарасов С.В., Бураков В.В. Способы реляционного моделирования иерархических структур данных // Информационно-управляющие системы. 2013. № 6 (67). С. 58–66.
Celko J. A Look at SQL Trees. DBMS, March 1996, pp. 27–36.
Henderson K. Guru's Guide to Transact SQL. Addison-Wesley Publ., 2000, 592 p.
Lennart J. Representing Trees in relational DB, 2001. URL: http://fungus.teststation.com/~jon/treehandling/TreeHandling.htm (дата обращения: 15.01.2016).
Lepekhin E. Trees in SQL databases, 2004. URL: http://www.codeproject.com/KB/database/Trees_in_SQL_databases.aspx/ (дата обращения: 15.01.2016).
Štih T. Modeling Hierarchies. 2002. URL: http://www.codeproject.com/KB/database/modhierarchies.aspx (дата обращения: 15.01.2016).
Tulder G. Storing Hierarchical Data in a Database. 2003. URL: http://www.sitepoint.com/print/hierarchical-data-database.htm (дата обращения: 15.01.2016).

Литература

Комментарии