Повышение уровня требований к качеству управления объектами различной природы обусловливает необходимость совершенствования алгоритмов обработки и анализа поступающей информации. Исследование рынка современных диагностических систем позволяет констатировать факт значительного увеличения видов объектов и оборудования, в котором реализуются диагностические процедуры. Это вызвано рядом факторов, в частности:

– снижением удельной стоимости вычислительных ресурсов;

– уменьшением размеров электронных схем и, соответственно, появлением возможности их применения для диагностики в устройствах, критичных к габаритам;

– повышением требований к экологической безопасности оборудования и технологических циклов производств;

– появлением новых методов обработки данных, позволяющих реализовывать ранее недоступные диагностические процедуры.

Отличительной чертой новых методов обработки выступает их интеллектуализация, чем достигается возможность анализа ситуаций на объекте на уровне экспертов с помощью экспертных систем. Примером такого применения может быть диагностическая система ЭСКСИСО для оценки состояния изоляционной системы маслонаполненного оборудования, дающая возможность отсрочить плановую замену еще работоспособного оборудования [1]. Другое применение интеллектуальных диагностических алгоритмов иллюстрируют комплексы «умный дом» – системы, обеспечивающие согласованную и автоматическую работу всех инженерных сетей дома, в функции которых входят и диагностика различных ситуаций, происходящих в жилом доме, и соответствующая реакция на них. При этом сама система строится по иерархическому принципу: одна из систем может управлять поведением других по заранее выработанным алгоритмам [2]. Интеллектуализация алгоритмов также позволяет расширять понятие диагностики на более высокие уровни иерархии систем управления и проводить диагностику состояний целых предприятий, оценивать риски нежелательных тенденций развития [3, 4].

Указанные аспекты отражают актуальность исследований в области совершенствования методов обработки информации в диагностических системах для объектов различной природы. В данной работе при выборе направлений исследований был учтен тот факт, что по своей сути диагностика является представителем так называемых обратных задач, относящихся к классу некорректно поставленных [5]. Методы решения этих задач часто сложны, поэтому мало представлены в диагностических алгоритмах. Другим учтенным обстоятельством было наличие шумов, поступающих от измерительной аппаратуры, которые вносят свой негативный вклад в общую процедуру контроля и распознавания ситуаций. Эти соображения привели к идее объединить решения этих проблем в одном алгоритме за счет использования оценивания состояния объектов при наличии шумов.

Присутствие некорректности требует применения специальных методов решения, которые можно разделить на точные и приближенные. Точные методы базируются на аналитических зависимостях между симптомами и причинами и сложны в применении. Кроме того, далеко не всегда такое решение удается получить ввиду сложности выкладок или принципиальной невозможности его нахождения. В этой связи востребованными остаются приближенные методы, базирующиеся на различных процедурах регуляризации [5–7], а также аппроксимационные подходы, позволяющие получать приемлемые с точки зрения использования на практике решения на основе численных схем, например, на основе применения
искусственных нейронных сетей [8–10]. Однако нейронные сети, хорошо решая задачи, сводящиеся к аппроксимации, имеют недостаток – не позволяют управлять процессом самого решения и вносить корректировки в алгоритм своей работы [11].

Один из методов регуляризации использует понятие фильтра Калмана и основан на применении метода квадратур при решении уравнений Фредгольма [5]. В частности, при рассмотрении интегрального уравнения Фредгольма I рода проводится замена интеграла конечной суммой, расписывая его, например, по формуле трапеций. В результате получается векторно-матричное уравнение, только по форме напоминающее описание дискретного формирующего фильтра, а дальше просто применяется калмановский алгоритм. Недостатком такого подхода, помимо его «искусственности», является то, что размерность матрицы системы зависит от количества интервалов разбиения: так, если область интегрирования разбивается всего на 10 участков, то количество столбцов матрицы возрастает до 11.

Предлагаемый метод решения обратных задач также базируется на применении фильтра Калмана и представлении исследуемого объекта в форме дифференциальных уравнений или соответствующих им разностных. Однако процессы, используемые при описании классического фильтра, как бы меняются местами – выходные рассматриваются как входные и наоборот. Для лучшего понимания излагаемого метода представим вначале краткую постановку задачи для фильтра Калмана для дискретного времени, не останавливаясь на описании параметров сигналов, что можно найти в соответствующей литературе [12].

Пусть состояние объекта в момент времени k получается из состояния в момент времени (k − 1) по правилу

Xk = Ak Xk-1 + Bk uk + vk,                                                    (1)

где Xk  – вектор состояния; Ak – матрица преобразования объекта; Bk – матрица управления uk,; vk – векторная случайная погрешность, имеющая нормальное распределение (на практике часто так оно и есть – на основании центральной предельной теоремы, так как на погрешность влияет совокупность большого множества неизвестных случайных факторов).

Измерения Yk производятся в дискретные моменты времени в соответствии с моделью

Yk = Сk Xk + Nk,

где Сk –  матрица модели наблюдения, отображающая пространство векторов состояния системы в пространство векторов результатов наблюдений; Nk – аддитивный шум измерений, который, как считается, имеет нулевое математическое ожидание и нормальное распределение.

Очевидно, что такая форма описания является приближенной для многих динамических систем, но, учитывая, что и фильтр Калмана предназначен для работы с зашумленными данными, результаты, получаемые фильтром, часто являются хорошим приближением к правильному ответу.

Оценка  состояния системы Xk вычисляется в соответствии с выражением, которое запишем в развернутом виде:

,                                              (2)

где Kk  – коэффициент усиления фильтра Калмана, который определяется на основании решения уравнения Риккати [12].

Приведенные уравнения кратко отражают классическую постановку задачи калмановской фильтрации. С другой стороны, на объектах АСУ ТП измерения производятся как на входе, так и на выходе объекта и оба этих измерения имеют соответствующую шумовую составляющую. Далее сам объект можно рассматривать не только как преобразователь входного сигнала в выходной, но и как реализующий обратную функцию, соответственно, применяя калмановский алгоритм, можно попробовать реализовать решение обратной задачи – оценка входного процесса по известному выходному.

В данном контексте встает вопрос физической реализуемости устройства, обеспечивающего оценку состояния для объекта, рассматриваемого с точки зрения обратного процесса, так как следствие не может наступить раньше причины. Здесь следует отметить, что задача оценивания разбивается на три подзадачи: сглаживания, фильтрации и экстраполяции. В задаче сглаживания проводится обработка результатов уже имеющихся измерений и в данном случае можно использовать дискретные отсчеты, опережающие рассматриваемый момент времени. Поэтому, абстрагируясь от пространственного соотношения процессов и рассматривая объект как преобразователь выходного сигнала во входной, можно сделать предположение о возможности инверсного применения фильтра по аналогии, например, как это уже используется в радиотехнике [13]. В таком случае описание объекта следует представить в форме, аналогичной (1):

Xrk = Dk Xrk-1 + Сk  + Nk,                                                                                                                                       (3)

где Xrk  – вектор состояния инверсной системы (здесь в обозначении используется добавочная буква r как первая буква в английском слове reverse); Dk – матрица инверсного преобразования.

На входе объекта измерения uk производятся в дискретные моменты времени в соответствии с моделью

urk = Lk Xrk + vk . 

По формуле, с точностью до обозначений аналогичной (2), находится оценка  состояния системы:

,

где Krk  – коэффициент усиления инверсного калмановского алгоритма сглаживания.

Уравнения (1), (3) представляют собой модели оцениваемой системы (объекта), структура их задана, но остается проблема определения матриц Ak и Dk соответственно, которые в стационарном случае не зависят от k. Структура предлагаемого алгоритма отражена на рисунке 1, где большинство обозначений уже введено ранее, кроме следующих: FLB – блок нечетко-логического вывода; FK – фильтр Калмана при обычной постанове задачи оценивания; OPT – процедура оптимизации для получения значений матрицы D, о чем будет сказано далее.

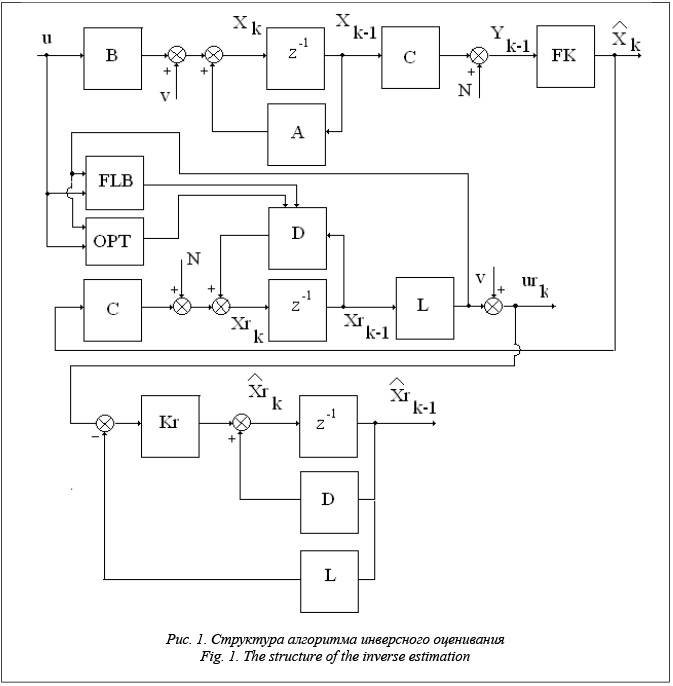
Если для (1) матрицу A можно определить исходя из физической взаимосвязи входных и выходных сигналов, то для D это сделать более затруднительно. Однако в данной ситуации становится оправданным применение подхода, базирующегося на нечетком логическом выводе, когда отправные значения элементов матрицы D формируются на основе базы знаний, сформированной экспертом, а дальнейшее их уточнение осуществляется оптимизационной процедурой. В основу базы знаний заложена система правил, учитывающая величину рассогласования выхода модели обратной системы и его измеренного значения на самой системе. Общая форма правил имеет вид:

,                                                                                              (4)

где TUj , TDUj – терм-множества для значений разности элементов и скорости изменения разности; TSUj, – терм-множества для значений разности элементов при формировании второй группы правил; TDi,j, TSDi,j  – терм-множества для элементов матрицы D в первой и второй группах правил соответственно; n1, n2 – количество правил; m1, m2, m3 – количество переменных, участвующих в правилах; Dkj = (LkXrk – uj) – (Lk–1Xr k–1 – uj) – разность текущих i-х значений процессов и предыдущих, отражающая скорость изменения значений процессов при переходе от отсчета с номером k–1 к отсчету с номером k.

Итерационная процедура, оптимизирующая настройку формирующего фильтра, имеет следующий вид (представлены фрагменты кода программы на языке MatLAB).

1. Задаются начальные значения элементов матрицы D.

2. Рассчитывается следующее значение выходного сигнала формирующего фильтра: Xm(1, i+1)=D*Xr(1, i)+v(1, i).

3. Вычисляется разность delta=Xm(1, i+1)-Xr(1, i+1).

4. Рассчитывается выход нечеткой системы BNV, содержащей базу правил вида (4): dD=evalfis(delta,BNV).

5. Выполняется коррекция модели D=D+dD.

6. Если обучающая выборка не закончена, осуществляется переход к п. 2.

7. Конец процедуры настройки.

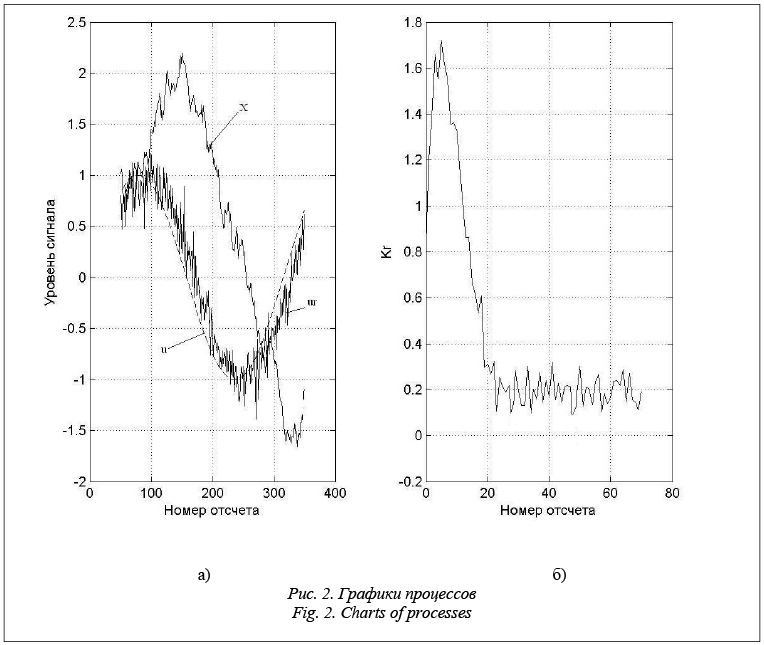
Математическое обоснование корректности предложенного метода решения обратных задач приводит к сложным выкладкам, поэтому ограничимся результатами модельного примера для линейного объекта. Пусть стационарный скалярный процесс с дискретными временем описывается уравнением вида xk+1 = xk  + 0.01u + v; yk  = xk + N. Другие исходные данные следующие: модель сигнала управления u=sin(0.02t); ковариация входного шума RV=0.004; ковариация выходного шума измерений QN=0.02.
Результаты расчетов отражены на рисунке 2. Как видно из рисунка 2а, оценка ur сигнала u имеет запаздывание по сравнению с самим сигналом u, однако форма и уровни сигнала ur имеют явное соответствие с сигналом u. Представляется, что для целей оценки корректности работы измерительной аппаратуры такое запаздывание может быть допустимо, так, такой углубленный анализ данных находится на верхнем уровне иерархии системы обработки измерительной информации, оставляя контроль аварийных ситуаций за нижними уровнями указанной системы. На рисунке 2б показано изменение коэффициента усиления инверсного фильтра в зависимости от шага расчета. После переходного процесса значение коэффициента усиления стабилизируется, что характерно для рекуррентных алгоритмов калмановского оценивания.

Кратко достигнутые результаты можно сформулировать следующим образом:

– предложен новый подход к решению обратных задач, базирующийся на калмановском подходе к задаче оценивания состояния объекта, но в инверсном рассмотрении сигналов и с применением нечетко-логической итерационной процедуры настройки параметров формирующего фильтра;

– представлены уравнения, отражающие соотношение сигналов и параметров алгоритмов прямого и инверсного оценивания;

– показаны результаты модельного эксперимента, демонстрирующие работоспособность инверсного оценивания по крайней мере для линейных объектов.

Предложенный подход еще требует детальной проработки, но уже полученные результаты позволяют сделать вывод о перспективности данного направления исследований.

Литература

1. Чернышев В.А., Кисляков М.А., Чернов В.А. Диагностическая система ЭСКСИСО, предназначенная для оценки состояния изоляционной системы маслонаполненного оборудования // Вестн. Мурманского гос. техн. ун-та. Вып. № 4. Т. 18. 2015. С. 729–739.

2. Джесси Р. Умный дом. М.: Изд-во VSD, 2013. 156 с.

3. Дли М.И., Гимаров В.В., Иванова И.В. Иерархические мультиагентные модели для управления телекоммуникационным предприятием // Журн. правовых и экономических исследований. 2012. № 4.
С. 86–89.

4. Мешалкин В.П., Белозерский А.Ю., Дли М.И. Методика построения комплексной математической модели управления рисками предприятия металлургической промышленности // Прикладная информатика. 2011. № 3 (33). С. 100–120.

5. Сизиков В.С. Обратные прикладные задачи и MatLab. СПб: Лань, 2011. 256 с.

6. Hansen P.C. Discrete Inverse Problems: Insight and Algorithms. Philadelphia: SIAM, 2010, 213 p.

7. Кривых А.В. Повышение разрешения спектроанализаторов на основе математической обработки измерительных данных: автореф. дис. … к.т.н. СПб, 2014. 23 c.

8. Пучков А.Ю., Павлов Д.А. Варианты построения алгоритма поиска решения обратных задач с применением нейронных сетей // Программные продукты и системы. 2012. № 2 (98). С. 149–153.

9. Puchkov A.Yu. Influence of the signal-noise ratio on the accuracy of the approximating metod of the solution of inverse problems. Proc. VII Intern. Research and Practice Conf. Germany, 2014, vol. II, pp. 543–546.

10. Павлов Д.А. Нечеткий фильтр Калмана в структуре алгоритма решения обратных задач для экономических объектов // Программные продукты и системы. 2013. № 4. С. 199–203.

11. Мешалкин В.П., Стоянова О.В., Дли М.И. Исследование искусственных нейронных сетей, используемых для моделирования свойств создаваемых композиционных наноматериалов // Изв. вузов: Химия и химическая технология. 2011. Т. 54. Вып. 5. С. 124-127.

12. Сейдж Э.П., Уайт Ч.С. III. Оптимальное управление системами; [пер. с англ.; под ред. Б.Р. Левина]. М.: Радио и связь, 1982. 392 с.

13. Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. М.: Радио и связь, 2004. 608 с.

 

 

INVERSE TASKS SOLUTION ON THE BASIS OF FUZZY INVERSE KALMAN ALGORITHM

(The work is written with the support of the grant of RFBR № 16-07-00491 А)

 

Dli M.I., Dr.Sc. (Engineering), Professor; Puchkov A.Yu., Ph.D. (Engineering), Associate Professor;
Malevich E.P., Undergraduate; putchkov63@mail.ru

(Smolensk Branch of the Moscow Power Engineering Institute, Energeticheskiy proezd 1, Smolensk, 214013, Russian Federation)

 

Abstract. The article is headlined the solution of the tasks of the ill-posed problems subclass, viz. inverse tasks of control systems dynamics, based on the Kalman state estimation application, that can be applied in different objects dynamics.

In contrast to a direct task, the process of the finding solution in an inverse task begins with the exit of the object and goes to the entry, meaning it is required to give an estimate to input actions that have leaded to the observing state, basing on the available information.

The Kalman filter algorithm application in reverse direction constitutes the novelty of the concerned solution structure, when the state of input process should be estimated on the basis of the observed output process. It is given the name of the filter – an “inverse filter” that characterizes the application feature.

During the Kalman filter implementation model construction in the form of differential equation, so-called forming filter is demanded, that needs complex calculations in a number of cases, in particular, process spectral characteristic factorization holding. The author proposes the iterational procedure of forming filter the parametric adjustment, based on fuzzy logic deduction, which is realized at the initial stage of the inverse task general algorithm application.

The results of the model experiment on the basis of the inverse Kalman type estimation software implementation in the programming environment MatLAB are represented in this article. These results have shown the probability of the proposed approach to the problem of inverse task solving application. Furthermore, the author describes the directions of the further researches within the chosen subject.

Keywords: inverse tasks, Kalman filter, fuzzy logic, data mining.