Проектирование СБИС – это сложный, занимающий много времени процесс. Одним из важнейших этапов в САПР ЭВА, результаты которого наиболее сказываются в производстве, является конструкторское проектирование [1–3]. Трудоемкость задач конструирования резко возрастает. Поэтому автоматизация конструкторского проектирования в связи с непрерывным изменением технологий производств и появлением новых элементов с большой степенью интеграции является актуальной и важной задачей. Все задачи, относящиеся к этому этапу, носят комбинаторно-логический характер и в основном являются NP-трудными и NP-полными. Непрерывно разрабатываются различные эвристики для нахождения квазиоптимальных решений за приемлемое время. Причем изменяющаяся технология ставит все новые задачи перед конструкторами электронно-вычислительной аппаратуры [4–6].
Среди этих задач сжатие топологии имеет особое значение, так как является одним из заключительных этапов конструкторского цикла проектирования. После выполнения детальной трассировки топологическая схема функционально готова. На этой стадии топология готова для создания микросхемы. Однако в результате неоптимальности размещения и трассировки в топологии присутствуют некоторые свободные пространства. Для уменьшения цены, улучшения характеристик и преимуществ топология сжимается в размерах удалением свободного пространства без изменения функциональности топологии. Эта операция уменьшения площади топологии называется сжатием топологии [7–10].
Цель сжатия топологии – минимизация общей площади топологии без нарушений правил проектирования, определенных проектировщиком. Площадь может быть минимизирована тремя путями:
– уменьшением пространства между элементами;
– уменьшением размеров каждого элемента;
– изменением формы элементов.
Сжатие топологии является комплексной фазой конструкторского этапа проектирования. Она требует понимания многих деталей процесса конструирования, таких, как правила проектирования.
Данная работа посвящена разработке алгоритма сжатия топологии СБИС на основе роевых методов, позволяющих получать более эффективные решения.
Постановка задачи сжатия топологии
Топология СБИС состоит из геометрических элементов (преимущественно прямоугольной формы). Каждый элемент соответствует компоненту схемы или проводнику [11–13]. Проблема сжатия формулируется следующим образом: имеется набор геометрических элементов M = {M1 , M2, …, Mn}, представляющих топологию. Для каждого элемента Mi задается минимальный размер s(Mi), определяемый правилами проектирования. Этими же правилами определяются минимальные интервалы, d(Mi, Mj), между элементами Mi и Mj, где 1 ≤ i, j ≤ n. Целью сжатия является минимизация общей площади топологии путем возможного изменения размеров элементов и их передвижением с соблюдением ограничений:
size (Mi) ≥ s(Mi),
dist (Mi, Mj) ≥ d( Mi, Mj),
где size(Mi) и dist(Mi, Mj) – размерыMi и расстояние между Mi иMj после сжатия, 1 ≤ i, j ≤ n. Если элемент s имеет фиксированные размеры, то задача сжатия заключается в переразмещении элементов топологии для уменьшения общей площади [8–10].
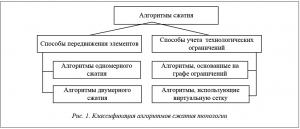
Алгоритмы сжатия могут быть классифицированы по двум направлениям (рис. 1).
Первое направление определяет, как компоненты перемещаются в ходе сжатия. В соответствии
с этим признаком алгоритмы делятся на алгоритмы одномерного и двумерного сжатия.
В первом случае компоненты топологии могут передвигаться только в одном направлении (по оси X либо по оси У) (рис. 2).
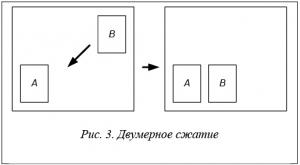
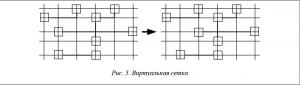
Для перемещения компонента по плоскости сначала осуществляется сжатие по одной оси, затем по другой. Во втором случае возможно передвижение компонента по двум направлениям (как по оси X, так и по оси У) (рис. 3).
Второе направление (признак) определяет принцип вычисления позиций размещаемых компонентов с соблюдением технологических ограничений. Этот класс образует два наиболее важных типа алгоритмов. Это алгоритмы, основанные на графе ограничений, и алгоритмы, использующие виртуальную опорную сетку.
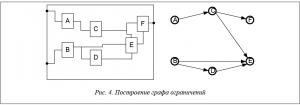
Граф ограничений строится по одному из направлений – X или Y. Ребро между вершинами существует в том случае, если соответствующие им объекты соседние и являются друг для друга препятствием (рис. 4).
Сжатие осуществляется просмотром графа ограничений в обратном направлении. Каждый раз при просмотре вершин определяется, на какое расстояние придвинуть смежные ей вершины. Но возможны и возвраты.
Алгоритмы, основанные на использовании виртуальной сетки, работают следующим образом. Через все компоненты проводятся линии, образуется сетка. Затем определяется минимальное расстояние между линиями сетки, при котором не будут нарушены технологические ограничения. Метод виртуальной сетки находит позиции элементов путем рассмотрения схемы. Он перемещает все компоненты на линию сетки вместе таким образом, что соседние линии виртуальной решетки находятся насколько возможно близко, пока удовлетворяют всем требуемым правилам разделения между символами на двух виртуальных сетках. Сеть деформируется (рис. 5).
Обширный класс алгоритмов сжатия, основанный на этих трех идеях, отличается способами организации поисковых процедур: либо это последовательные, либо итерационные, либо алгоритмы случайного поиска и т.д. Во многих алгоритмах используется комбинированный подход, когда эти идеи применяются одновременно. Для сложных схем используется иерархический подход, когда элементы (ячейки) нулевого уровня объединяются в блоки первого уровня и далее. Сжатие последовательно проводят в элементах 0-го уровня, 1-го уровня и т.д.
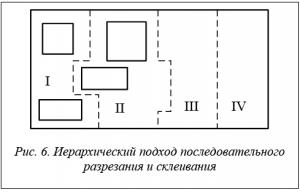
Существует иерархический подход последовательного разрезания и склеивания. Вначале топологический чертеж разрезается на части вертикальными сечениями. При этом вертикальные сечения проводятся таким образом, чтобы они не проходили через элементы топологии (рис. 6).
Образуются области с неизменяемой конфигурацией границ. Затем последовательно и независимо друг от друга производится компакция в каждой области по оси X.
После этого области склеиваются в единый чертеж. Затем аналогичным образом проводятся горизонтальные сечения, которые также разбивают чертеж на области, в которых осуществляется компакция по оси Y. Общая процедура подразумевает чередование этих процедур до тех пор, пока возможно сжатие.
Разработка общей структуры алгоритма
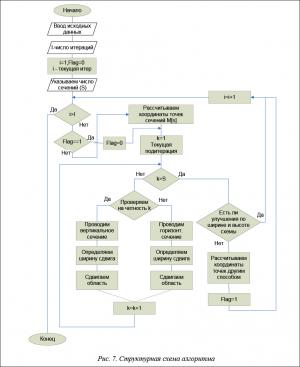
В работе используется подход, при котором задача сжатия на плоскости решается алгоритмом одномерного сжатия, основанным на использовании виртуальной сетки [5–8]. Компоненты топологии могут передвигаться только в одном направлении (по оси X либо по оси У). Для перемещения компонентов по плоскости поочередно осуществляется сжатие по одной оси, затем по другой. Предложенный алгоритм основан на применении так называемых сечений (путей) деформации (сжатия) (рис. 7). Сечение деформации должно соединять противоположные края рисунка топологии, не должно пересекать ни одной параллельной ему трассы и ни одного компонента. Если такой путь найти не удается, делается попытка построить путь ломаной формы, применяя лабиринтный алгоритм для обхода препятствий. После определения путей деформации определяется ширина сдвига области. Для этого используется модифицированный алгоритм Ли – метод соединения комплексами [10, 11]. После этого производится сдвижение областей.
Основные пункты разработанного алгоритма.
1. Начало. Вводятся исходные данные. Загружается исходная схема. Задаются число итераций (I) и число сечений (S) на подитерациях.
2. Проверяется условие на количество итераций: i > I, где i – текущая итерация. Если условие выполняется, осуществляется переход к пункту 13, иначе переход к пункту 3.
3. Проверяется условие Flag = 1. Если условие выполняется, то Flag = 0 и осуществляется переход к пункту 5, иначе переход к пункту 4.
4. Рассчитываем координаты точек сечений. Для проведения как горизонтального, так и вертикального сечения необходима только начальная точка сечения. В начальной точке для горизонтального сечения генерируется только координата y, а координата x приравнивается к 0. И наоборот, для вертикального сечения горизонтальные и вертикальные сечения проводятся равномерно по всей ширине и высоте схемы. Для их проведения рассчитывается приращение по x (dx) и по y ( dy). Определяется количество горизонтальных и вертикальных сечений. Для этого в ряду 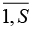 определяется количество четных и нечетных чисел, которое будет соответствовать количеству вертикальных (V) и горизонтальных (H) сечений соответственно. Рассчитываются приращения по x и по y по формулам dx = F2/V, dy = F1/H, где F 1 и F2 – высота и ширина схемы. Тогда массив координат начальных точек будет заполнен следующим образом: M[S] = [Sdy-a1, Sdx-a2, (S–1)dy, (S–1)dx, (S–2)dy, (S–2)dx, …, 3dy, 3dx, 2dy, 2dx, dy, dx], где a1, a2 – отступы от краев по ширине и высоте схемы.
определяется количество четных и нечетных чисел, которое будет соответствовать количеству вертикальных (V) и горизонтальных (H) сечений соответственно. Рассчитываются приращения по x и по y по формулам dx = F2/V, dy = F1/H, где F 1 и F2 – высота и ширина схемы. Тогда массив координат начальных точек будет заполнен следующим образом: M[S] = [Sdy-a1, Sdx-a2, (S–1)dy, (S–1)dx, (S–2)dy, (S–2)dx, …, 3dy, 3dx, 2dy, 2dx, dy, dx], где a1, a2 – отступы от краев по ширине и высоте схемы.
5. Проверяется условие на количество подитераций: k > S, где k – текущая подитерация. Если условие выполняется, то переход к пункту 10, иначе переход к пункту 6.
6. Проверяется условие на четность подитерации (k). Если условие выполняется, то переход к пункту 7, иначе переход к пункту 8.
7. Проводится вертикальное сечение лабиринтным алгоритмом. Координата начальной точки сечения берется из массива M[k–1] .
8. Определяется ширина сдвига методом соединения комплексами. Сдвигаем области. Переход к пункту 9.
9. Проводится горизонтальное сечение лабиринтным алгоритмом. Координата начальной точки сечения берется из массива M[k –1] .
10. Определяется ширина сдвига методом соединения комплексами. Сдвигаем области. Переход к пункту 9.
11. Увеличиваем подитерацию на один: k = k+1. Переход к пункту 5.
12. Проверяется условие: есть ли улучшения по ширине (F 2) и высоте (F1) схемы. Если условие выполняется, то переход к пункту 11, иначе переход к пункту 12.
13. Увеличиваем итерацию на один: i = i+1. Переход к пункту 2.
14. Случайно генерируем координаты точек сечений. Flag = 1. Переход к пункту 11. Конец.
Механизмы сжатия топологии СБИС на основе поведения муравьиной колонии
Пусть дан граф G(X, U), где Х – множество вершин, |X| = n, U – множество ребер. Необходимо разбить множество X на два непустых и непересекающихся подмножества 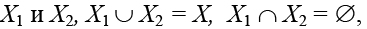
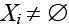 . На формируемые узлы (блоки, компоненты) накладываются ограничения: |X1| = n1, |X2| = n2, n1 + n2= n. Критерий оптимизации – число связей F между X1 и X2. Цель оптимизации – минимизация критерия F.
. На формируемые узлы (блоки, компоненты) накладываются ограничения: |X1| = n1, |X2| = n2, n1 + n2= n. Критерий оптимизации – число связей F между X1 и X2. Цель оптимизации – минимизация критерия F.
Для поиска решения задачи используется полный граф решений R( X, E), где E – множество всех ребер полного графа, связывающих множество вершин X. На множестве ребер E будем откладывать феромон. На начальном этапе на всех ребрах графа R откладывается одинаковое (небольшое) количество феромона Q/m, где m = |E|. Каждый из агентов формирует множество X1 k, где k – номер агента. Формирование множества X1k осуществляется последовательно (пошагово). На каждом шаге t у k-го агента есть список вершин, уже включенных в формируемое множество – X1k(t) и список оставшихся (свободных) вершин 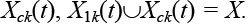 На первом шаге в каждое формируемое множество X1k(t), где t = 1, включается вершина графа G, причем вершины графа G распределяются по узлам равномерно, то есть в каждом узле своя вершина,
На первом шаге в каждое формируемое множество X1k(t), где t = 1, включается вершина графа G, причем вершины графа G распределяются по узлам равномерно, то есть в каждом узле своя вершина,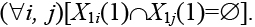 Такое распределение необходимо, чтобы все вершины графа G имели одинаковые шансы быть отправной точкой при формировании узла X1. В модификациях алгоритма использовались также ln муравьев, причем каждая группа изl муравьев использует в качестве начального одно и то жеX1i(1). На конечном шаге t = n1 k-м агентом будет сформирован узел X1k (n1) = X1k. |X1( n1)| = n1.
Такое распределение необходимо, чтобы все вершины графа G имели одинаковые шансы быть отправной точкой при формировании узла X1. В модификациях алгоритма использовались также ln муравьев, причем каждая группа изl муравьев использует в качестве начального одно и то жеX1i(1). На конечном шаге t = n1 k-м агентом будет сформирован узел X1k (n1) = X1k. |X1( n1)| = n1.
Моделирование поведения муравьев в задаче сжатия топологии связано с распределением феромона на ребрах графа R [14, 15]. При этом вероятность включения вершины 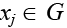 в формируемое отдельным муравьем множество X1k(t) пропорциональна суммарному количеству феромона на ребрах, связывающих вершину xjс X1k( t). Количество откладываемого феромона пропорционально числу связей между сформированными узлами. Чем меньше число связей междуX1k и X2k, тем больше феромона будет отложено на ребрах полного подграфа
в формируемое отдельным муравьем множество X1k(t) пропорциональна суммарному количеству феромона на ребрах, связывающих вершину xjс X1k( t). Количество откладываемого феромона пропорционально числу связей между сформированными узлами. Чем меньше число связей междуX1k и X2k, тем больше феромона будет отложено на ребрах полного подграфа 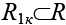 , построенного на вершинах узла X1k, следовательно, большее количество муравьев будет включать вершины узла X1k в синтез собственных узлов. Для избегания преждевременной сходимости используется отрицательная обратная связь в виде испарения феромона [15]. Процесс поиска решений итерационный. Каждая итерация t включает три этапа. На первом этапе муравей находит решение, на втором этапе откладывает феромон, на третьем осуществляется испарение феромона. В работе используется циклический (ant-cycle) метод муравьиных систем. В этом случае феромоны откладываются агентом на ребрах после полного формирования решения [14, 15].
, построенного на вершинах узла X1k, следовательно, большее количество муравьев будет включать вершины узла X1k в синтез собственных узлов. Для избегания преждевременной сходимости используется отрицательная обратная связь в виде испарения феромона [15]. Процесс поиска решений итерационный. Каждая итерация t включает три этапа. На первом этапе муравей находит решение, на втором этапе откладывает феромон, на третьем осуществляется испарение феромона. В работе используется циклический (ant-cycle) метод муравьиных систем. В этом случае феромоны откладываются агентом на ребрах после полного формирования решения [14, 15].
На первом этапе каждой итерации каждый k-й муравей формирует свое собственное множество X1k. Процесс построения множества X1k пошаговый. На каждом шаге агент применяет вероятностное правило выбора следующей вершины для включения ее в формируемое множество X1 k(t).
Первый этап осуществляется следующим образом. Агент просматривает все свободные на данном шаге вершины Xсk(t). Для каждой вершины 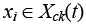 рассчитываются два параметра:
рассчитываются два параметра:
– fik – суммарный уровень феромона на ребрах графаR, связывающих xi с вершинами узла X 1k(t);
– sik – число связей на графе G междуxi и X1k( t).
Потенциальная стоимость Fik связейxi с Xс k(t) при мультипликативной свертке определяется по формуле
Fik = (fik)α·(sik+1) β, (1)
при аддитивной свертке по формуле
Fik = (fik)α + (sik) β, (2)
где α, β – управляющие параметры, которые подбираются экспериментально.
Вероятность Pik включения вершины 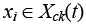 в формируемый узел X1k(t) определяется следующим соотношением:
в формируемый узел X1k(t) определяется следующим соотношением:
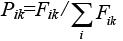 (3)
(3)
Агент с вероятностью Pik выбирает одну из вершин, которая включается в множество X1k(t) и исключается из множества Xс k(t).
При α = 0 наиболее вероятен выбор вершины xi, максимально связанной с вершинами узла X 1k(t), то есть алгоритм становится жадным.
При β = 0 выбор происходит только на основании феромона, что приводит к субоптимальным решениям.
Поэтому необходим компромисс между этими величинами, который находится экспериментально.
После формирования за n шагов муравьями узлов (у каждого муравья свой узел X1k) на втором этапе итерации каждый муравей откладывает феромон на ребрах полного подграфа 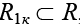 , построенного на вершинах узла X1k.
, построенного на вершинах узла X1k.
Количество феромона Dτk(l), откладываемое k-м муравьем на каждом ребре подграфа ![]() , построенного на l-й итерации, определяется следующим образом:
, построенного на l-й итерации, определяется следующим образом:
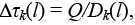 (4)
(4)
где l – номер итерации; Q – общее количество феромона, откладываемое k-м муравьем на ребрах подграфа 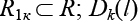 – число связей на графе G между множествами X1k и X2k, сформированными k-м муравьем на l-й итерации. (Другими словами, целевая функция для данного решения.)
– число связей на графе G между множествами X1k и X2k, сформированными k-м муравьем на l-й итерации. (Другими словами, целевая функция для данного решения.)
После того как каждый агент сформировал решение и отложил феромон, на третьем этапе происходит общее испарение феромона на ребрах полного графа R в соответствии с формулой
Fik = fik(l – ρ), (5)
где ρ – коэффициент обновления (0.93–0.99).
После выполнения всех действий на итерации находится агент с лучшим решением, которое запоминается. Далее осуществляется переход на следующую итерацию. Временная сложность этого алгоритма зависит от времени жизни колонии l (число итераций), количества вершин графа n и числа муравьев m и определяется как O(l∙n 2∙m).
Экспериментальные исследования
В данной работе проводились экспериментальные исследования в целях установления эффективности алгоритма сжатия топологии СБИС.
Основная цель экспериментальных исследований – оценка трудоемкости алгоритма: зависимость времени работы от размеров топологической схемы, а также исследования влияния на плотность элементов [15].
Перед началом экспериментов необходимо определить порядок их проведения, чтобы за счет оптимального планирования с минимальными затратами получить всю информацию относительно объектов исследования.
Для получения объективных оценок в результате экспериментов и составления достоверных выводов необходимо провести серию экспериментов для различных тестовых примеров, определяя время работы. В качестве критерия эффективности алгоритма принимается максимальное найденное значение целевой функции за определенное число итераций.
Для подтверждения теоретических оценок ВСА необходимо исследовать зависимость быстродействия от числа вершин гиперграфа.
Экспериментальные исследования состояли из двух частей.
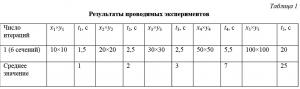
В первой части исследовалась зависимость времени сжатия от размера топологической схемы. Каждый экспериментальный опыт проводился десять раз, координаты задавались случайным образом, из полученных результатов рассчитывалось среднее значение. Приведем ряд результатов, полученных в проводимых экспериментах (табл. 1).
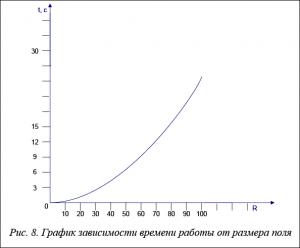
На рисунке 9 приведен график зависимости времени работы от размеров коммутационного поля, зависимость квадратичная.
В результате эксперимента было установлено, что оценка трудоемкости имеет вид О(n2), где n – число связываемых контактов, и совпадает с теоретической оценкой.
Во второй части исследований разработанный алгоритм сравнивался с аналогичными алгоритмами [14, 15]. В таблице 2 приведены результаты: показатели (в процентах) уменьшения площади СБИС после сжатия с помощью разработанного алгоритма А3 в сравнения с алгоритмом А1 (Boyer) и алгоритмом А2 (Eichenberger).
Таким образом, разработанный алгоритм сжатия топологии СБИС на основе роевых методов в среднем на 3 % эффективнее аналогичных алгоритмов.
Работа выполнена при финансовой поддержке гранта РФФИ № 17-07-00997.
Литература
1. Малышев И.В., Немудров В.Г. Состояние и перспективы отечественных разработок СБИС типа «система на кристалле» // Системы и средства связи, телевидения и радиовещания. 2003. №. 1, 2. С. 56–57.
2. Норенков И.П. Основы автоматизированного проектирования. М.: Изд-во МГТУ им. Н.Э. Баумана, 2009. 430 с.
3. Курейчик В.М., Лебедев Б.К., Лебедев В.Б. // Решение задач оптимизации и проектирования схем ЭВА на основе использования гибридных интеллектуальных методов: Проблемы разработки перспективных микро- и наноэлектронных систем-2010 (МЭС-2010): сб. трудов IV Всерос. науч.-технич. конф. «Проблемы разработки перспективных микро- и наноэлектронных систем-2010 (МЭС-2010)». М.: Изд-во ИППМ РАН, 2010. С. 170–178.
5. Dorigo M. and Stützle T. Ant Colony Optimization. MIT Press, Cambridge, MA, 2004, 328 p.
6. Кулиев Э.В., Лежебоков А.А. Исследование характеристик гибридного алгоритма размещения // Изв. ЮФУ. Технич. науки. Тематич. вып. Интеллектуальные САПР. 2003. № 3 (140). С. 255–261.
7. Запорожец Д.Ю., Кудаев А.Ю., Лежебоков А.А. Многоуровневый алгоритм решения задачи параметрической оптимизации на основе биоинспирированных эвристик // Изв. КБНЦ РАН. 2013.
№ 4 (54). С. 21–29.
8. Lebedev B.K., Lebedev O.B., Lebedeva E.O., Kostyuk A.I. VLSI planning based on the ant colony method . Advances in intelligent and computing. Proc. 2nd Intern. SciConf. IITI’18, Springer, Czech Republic, 2018, vol. 1, pp. 388–397.
9. Alpert C.J., Mehta D.P., and Sapatnekar S.S., Handbook of algorithms for physical design automation. Boston, MA. Auerbach, 2009, 1044 p.
10 Лебедев Б.К., Лебедев В.Б., Лебедев О.Б. Гибридизация роевого интеллекта и генетической эволюции на примере размещения // Программные продукты, системы и алгоритмы. 2017. № 4. URL: http://swsys-web.ru/hybridization-of-swarm-intelligence-and-genetic-evolution.html (дата обращения: 12.03.2018).
11 Курейчик В.М., Кажаров А.А. Использование роевого интеллекта в решении NP-трудных задач // Изв. ЮФУ. Технич. науки. 2011. № 7. С. 30–36.
12 Clerc M. Particle Swarm Optimization. ISTE, London, UK, 2006.
13. Лебедев Б.К., Лебедев О.Б., Лебедева Е.М. Муравьиный алгоритм построения бинарного дерева решений // Изв. ЮФУ. Технич. науки. № 7 (180). С. 74–88.
14. Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой. М: Изд-во МГТУ им. Н.Э. Баумана, 2014. 446 с.
15. Poli R. Analysis of the publications on the applications of particle swarm optimisation. Jour. of Artificial Evolution and Applications, 2008, Article ID 685175, 10 p.


Комментарии