Определение координат и скоростей динамических объектов с максимально возможной точностью по наблюдаемым измерениям, формируемых системой ГЛОНАСС, является центральной задачей любой системы слежения в гражданской сфере.
Точность навигации зависит от количества спутников в используемом созвездии и их взаимного расположения. Кроме того, данные о позиции транспортного средства постоянно меняются, проявляется своего рода шум, связанный с движением спутников, отражением от поверхности, процессами в атмосфере и излучением со стороны солнца, влияющими на сигнал [1].
В навигационной аппаратуре потребителей системы ГЛОНАСС выполняются измерения псевдодальности и радиальной псевдоскорости до четырех спутников ГЛОНАСС, а также прием и обработка навигационных сообщений, содержащихся в составе спутниковых навигационных сигналов (СНС). Помимо основной функции – навигационных определений, система позволяет производить высокоточную взаимную синхронизацию стандартов частоты и времени на удаленных наземных объектах и взаимную геодезическую привязку. Кроме того, с ее помощью можно определять ориентацию объекта на основе измерений, производимых от четырех приемников сигналов навигационных спутников.
Навигационная аппаратура пользователя выдает значения координат и проекций скорости транспортного средства в дискретные моменты времени через заданный интервал посредством их расчета по псевдодальностям до космического аппарата. Псевдодальности рассчитываются по временным задержкам Tt сигнала по трассе «i-й космический аппарат–потребитель» и известной скорости распространения радиоволн. Рассмотрим случай определения двухмерных координат навигационного подвижного объекта (НПО) в некоторой (любой) двухмерной прямоугольной системе координат [2, 3].
Постановка задачи
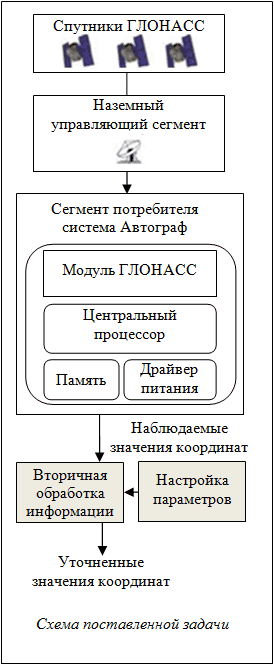
В настоящей статье рассматривается задача оценивания вектора системы на основании наблюдения ее выхода с учетом случайных возмущений и ошибок измерений. Задача наблюдения, сформулированная в стохастических терминах, именуется задачей фильтрации, ее общая схема представлена на рисунке.
Чтобы предложить один из вариантов вторичной обработки показаний аппаратуры пользователя СНС, необходимо записать достаточно общую формальную дискретную модель движения НПО.
 Для моделирования и расчетов необходимых параметров местоположения объекта необходимо представить все рассмотренные модели в дискретном времени. Учитывая инерционность объектов и малые интервалы ti – ti-1 = ∆t временной дискретизации, можно ограничиться линейным приближением производных в общей модели.
Для моделирования и расчетов необходимых параметров местоположения объекта необходимо представить все рассмотренные модели в дискретном времени. Учитывая инерционность объектов и малые интервалы ti – ti-1 = ∆t временной дискретизации, можно ограничиться линейным приближением производных в общей модели.
В дискретные равноотстоящие на малую величину ∆t моменты времени t1, t2, …, tk, tk+1, … для двухмерных координат xi(k) и проекций скорости vi(k) НПО на оси двухмерной прямоугольной системы координат модель изменения от момента к моменту представим в виде
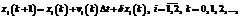 (1)
(1)
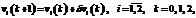 (2)
(2)
где dxi (k) и dмi (k) будем называть возмущениями координат и проекций скорости соответственно, которые могут содержать случайную и регулярную составляющие и обусловлены криволинейностью траектории НПО и наличием ненулевых ускорений и их производных [4].
Целевую функцию задачи оптимизации удельного расхода топлива зададим в следующем виде:
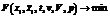 при
при 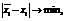 (3)
(3)
где xi – действительные значения координат объекта; 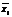 – наблюдаемые значения координат объекта; v – скорость подвижного объекта; V – удельный расход топлива; p – прочие факторы, влияющие на объем удельного расхода топлива.
– наблюдаемые значения координат объекта; v – скорость подвижного объекта; V – удельный расход топлива; p – прочие факторы, влияющие на объем удельного расхода топлива.
Целевая функция задана неявно, так как достаточно трудно учесть все параметры, влияющие на расход топлива. Неявное задание целевой функции означает, что в алгоритме оптимизации не будет использоваться алгебраическое выражение функции пригодности, так как полное описание всех параметров, влияющих на расход топлива, приведет к очень сложному и громоздкому алгебраическому выражению, на расчет которого потребуется недопустимое количество машинного времени.
Критерием остановки алгоритма может быть как время поиска, так и динамика изменения целевой функции, возможно также объединение двух этих критериев остановки.
Алгоритм Калмана
В радиолокационных станциях автоматического сопровождения и обработки сигналов в инерциальных навигационных системах наиболее распространенным алгоритмом вторичной обработки является фильтр Калмана.
В алгоритме типа многомерной калмановской фильтрации начальными условиями на каждом новом цикле служат оценка состояния системы и величина, характеризующая ее погрешность. Данный алгоритм последовательно обрабатывает заново поступающие векторы измерений, учитывая при этом значения, вычисленные на предшествующем цикле. Эта черта отличает способ фильтра Калмана от нерекуррентных алгоритмов, которым ради работы требуется оберегать целый массив обрабатываемых данных. На следующем шаге с помощью обрабатываемых на данном цикле измерений уточняются начальные условия. По мере последовательной обработки новых измерений происходит накопление фильтром полезной информации, вследствие этого суммарная погрешность оценок, как правило, должна снижаться [4], если элементы вектора состояния твердо выражаются сквозь измеренные величины.
Алгоритм расширенного фильтра Калмана представляется следующим образом:
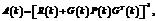 (4)
(4)
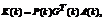 (5)
(5)
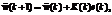 (6)
(6)
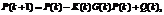 (7)
(7)
где вектор 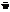 – оценка состояния системы на k-м шаге. Эта оценка является функцией от матрицы усиления Калмана K(k) и вектора ошибки
– оценка состояния системы на k-м шаге. Эта оценка является функцией от матрицы усиления Калмана K(k) и вектора ошибки 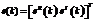 . Матрица усиления Калмана является функцией от ковариационной матрицы приближенной ошибки P(k), матрицы градиента G(k) и матрицы A(k). Наконец, матрица A(k) является функцией от ковариационной матрицы шума наблюдения R(k), матриц P(k) и G(k) [3, 4].
. Матрица усиления Калмана является функцией от ковариационной матрицы приближенной ошибки P(k), матрицы градиента G(k) и матрицы A(k). Наконец, матрица A(k) является функцией от ковариационной матрицы шума наблюдения R(k), матриц P(k) и G(k) [3, 4].
Нейросетевой подход
Один из основных недостатков представленного метода фильтрации состоит в том, что для построения алгоритма на основе фильтра Калмана требуется исчерпывающая априорная информация о свойствах оцениваемых процессов и ошибок их измерений. Кроме того, реализация фильтра Калмана характеризуется низкой скоростью сходимости [5].
Одним из перспективных подходов к решению данной задачи является использование теории нейронных сетей. Нейронные сети применяются в измерительных приложениях достаточно давно. Однако такие вопросы, как оптимальный выбор архитектуры нейронной сети, выбор алгоритма обучения и исследование метрологических характеристик нейросетевых моделей, а также применение нейронных сетей, остаются открытыми.
Основная идея использования многослойного персептрона в качестве фильтра для сглаживания и экстраполяции координат основывается на известной способности нейронных сетей проводить экстраполяцию временного ряда. Поступающие на вход вторичной обработки координаты обнаруженных отметок представляют собой временной ряд, только имеющий векторный вид.
В основе нейросетевой технологии лежит концепция распределенных адаптивных нелинейных вычислений. Нейронные сети строятся из большого числа простых элементов, каждый из которых обрабатывает свою часть единой задачи. Принципы вычислений для стандартного элемента достаточно просты. Вся мощь нейронных сетей основывается на множестве взаимосвязей между этими простыми элементами, которые совместно участвуют в решении задачи, а также в адаптивной настройке параметров (весов), связывающих элементы между собой.
В настоящее время известно очень много различных нейросетевых моделей, или парадигм, как их принято называть в литературе, посвященной теории нейронных сетей [5, 6].
При проведении настоящего исследования среди нейросетевых моделей авторами выбрана модель трехслойного персептрона, которая имеет достаточно прочное экспериментальное обоснование; при ее анализе могут быть применены результаты статистической теории. В качестве алгоритма обучения нейронной сети выбран классический алгоритм обратного распространения ошибки и алгоритм, использующий результаты фильтра Калмана. Помимо реализации стандартной вычислительной процедуры оценки вектора состояния движущегося объекта, фильтр Калмана находит применение в качестве алгоритма обучения искусственной нейронной сети. В отличие от наиболее распространенного алгоритма обратного распространения фильтр Калмана позволяет избежать многих недостатков, характерных для метода градиентного спуска, лежащего в его основе. При обучении с помощью фильтра Калмана искусственная нейронная сеть представляет собой нелинейную динамическую систему, состояние которой задается множеством синаптических связей. Выходные значения параметров, измеряемые фильтром, принимаются равными желаемому отклику нейронной сети. Таким образом, нейронная сеть привлекается для уточнения оценок, вырабатываемых в фильтре Калмана.
Методы параметрической идентификации
Один из наиболее общих подходов к решению задачи повышения точности оценки неизвестных параметров динамической системы заключается в использовании методов параметрической идентификации [2, 3]. Традиционно при разработке практических алгоритмов используются методы идентификации, базирующиеся на принципах регрессионного анализа и статистического синтеза.
Задача восстановления зависимостей по эмпирическим данным в общей постановке выглядит следующим образом. Есть набор данных Х, каждый элемент которого характеризуется вектором признаков (параметров) ξ=(x1, x2, ..., xN), множество ответов Y и множество отображений (функций) U из X в Y. Существует отображение y*: X →Y (необязательно принадлежащее U), значения которого априорно известны только на конечном наборе элементов y(n) = y* (ξ(n)), n = 1, ..., N (обучающей выборке).
Требуется по априорной информации построить функцию y=f*(ξ), f*∈U, наилучшим образом восстанавливающую зависимость не только на элементах обучающей выборки, но и на всем множестве объектов X [5].
Рассмотрим задачу восстановления регрессии, используя среднеквадратичный критерий близости как функционал качества:
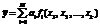 (8)
(8)
Наиболее распространенные варианты решения задачи восстановления регрессии следующие.
1) Линейная и полиномиальная аппроксимации. Будем искать аппроксимацию в классе линейных по параметрам функций 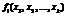 , где
, где 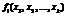 – заданные заранее функции; ai – неизвестные коэффициенты. Если
– заданные заранее функции; ai – неизвестные коэффициенты. Если 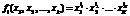 , где
, где 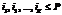 – степень полинома, получим аппроксимацию полиномиальной функцией степени P.
– степень полинома, получим аппроксимацию полиномиальной функцией степени P.
2) Древовидная аппроксимация. Суть анализа с помощью построения деревьев регрессии сводится к нахождению множества условий «если–тогда». Таким образом, разделяя множество исходных наблюдений, требуется минимизировать ошибку предсказания.
Применим оба метода к задаче идентификации динамического объекта по зашумленным измерениям в режиме реального времени.
Реализация
Для решения задачи фильтрации данных разработана программа в среде Delphi, осуществляющая реализацию рассмотренных методов, алгоритма обратного распространения ошибки и алгоритма, основанного на результатах фильтра Калмана для обучения построенной нейронной сети, методов параметрической идентификации.
Для сравнения качества работы рассмотренных алгоритмов использовались данные, полученные с помощью навигационной аппаратуры фирмы «Техноком» (г. Москва) об отдельном рейсе транспортного средства, отражающие динамику движущегося объекта в течение 10 часов. В качестве тестирующего множества использованы данные о динамике транспортного средства в течение другого рейса.
Для оценки точности построенной регрессии применялась оценка по тестовой выборке, когда вся совокупность наблюдений разбивается на пару подвыборок Z1 и Z2 (в качестве Z2 возьмем наблюдения за другой рейс). Оценка среднеквадратической ошибки по тестовой выборке проводится следующим образом: пусть учебная выборка Z размера N разбита на подвыборки Z1 и Z2 размером N1 и N2 соответственно, тогда
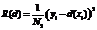 , (9)
, (9)
где Z2 – подвыборка, которую не использовали при построении предиктора.
Таким образом, повышение точности оценивания в режиме реального времени состояний и параметров динамических систем по зашумленным измерениям выходных переменных по-прежнему представляет актуальную проблему оценки состояния, которая включает в себя решение задач сглаживания и фильтрации.
На основании полученных в результате тестирования данных можно говорить о преимуществе использования построенной нейронной сети в задаче уточнения наблюдаемых параметров движущихся объектов в системе ГЛОНАСС по сравнению с работой фильтра Калмана, методов параметрической идентификации, хотя метод построения деревьев регрессии показывает более высокую скорость построения функции аппроксимации.
Предложенный нейросетевой подход может быть использован при построении программно-инструментальных средств для определения местоположения подвижных объектов в реальном масштабе времени. Это позволит более точно определить координаты, а значит, уменьшить стоимость затрат на топливо в процессе наблюдения за транспортным средством.
Литература
1. Решетников В.Н. Космические телекоммуникации. Системы спутниковой связи и навигации. СПб: Ленинград изд-во, 2010. 134 с.
2. Карабутов Н.Н. Адаптивная идентификация систем: информационный синтез. М.: КомКнига, 2006.
3. Понятский В.М. Исследование способов реализации адаптивной системы управления с фильтром Калмана // Стохастическая оптимизация в информатике. 2008. Т. 4. № 1-1. С. 196–210.
4. Сучилин В.И., Волобуев Г.Б. Оценка возможностей повышения точности местоопределения наземного подвижного объекта путем вторичной обработки показаний аппаратуры пользователя систем GPS NAVSTAR и/или ГЛОНАСС // Кибернетика и высокие технологии XXI века: сб. докл. VIII Междунар. науч.-технич. конф. Воронеж. 2007. Т. 2. С. 1066–1073.
5. Сергеев В.В., Копенков В.Н., Чернов А.В. Сравнительный анализ методов аппроксимации функций в задачах обработки изображений // Автометрия. 2006. Т. 42. № 2. С. 100–106.
6. Чернодуб А.Н., Новицкий Д.В., Дзюба Д.А. Прогнозирование временных рядов на основе одиночных нейронных сетей и комитетов нейронных сетей: сравнительный эксперимент // НЕЙРОИНФОРМАТИКА-2011: XIII Всерос. науч.-технич. конф. М., 2011. Ч. 2. С. 192–201.
7. Болодурина И.П., Решетников В.Н., Таспаева М.Г. Методы уточнения интегрированного наземно-космического мониторинга в системе ГЛОНАСС // Программные продукты и системы. 2011. № 4. С. 130–134.
Комментарии