Объем сохраняемых данных в наше время растет экспоненциально. Если данные сохраняют, то, как писал поэт, это кому-то нужно. Анализ данных позволяет выявлять присущие им закономерности. Статистика, занимающаяся сбором и анализом данных, является одной из древнейших наук. Математическая статистика предложила рассматривать собираемые данные как выборки из генеральной совокупности возможных значений случайных величин и случайных процессов. Теория вероятности изучает закономерности, присущие случайным величинам, законы их распределения, характеристики этих законов. Математическая статистика, оперируя с данными, позволяет выяснить, какому закону распределения и какой генеральной совокупности подчиняется сделанная выборка. Такой подход позволяет решать самые разные практические задачи, связанные с классификацией данных, прогнозированием, установлением оптимальных значений.
Вероятностный подход далеко не единственный подход, получивший широкое распространение при анализе собираемых данных. Можно упомянуть такие подходы, как экспертные системы, генетические алгоритмы, нейронные сети. Все они так или иначе занимаются выявлением скрытых закономерностей, присущих данным. Для этой деятельности Григорий Пятецкий-Шапиро предложил термин Data Mining, ставший весьма популярным. Буквально этот термин означает «раскопки данных», чаще всего переводится как «интеллектуальный анализ данных» или «извлечение знаний из данных» (Knowledge Data Discovery – KDD) [1].
Одним из важных алгоритмов, характерных именно для процесса извлечения знаний из данных, является алгоритм обнаружения в данных ассоциативных правил. Алгоритм «Априори» (Apriori), предложенный Р. Аграваем и Р. Шрикантом в 1994 году [2], позволил строить ассоциативные правила для больших БД, избегая полного перебора вариантов. Многочисленные реализации этого алгоритма стали основой различных инструментальных систем, поддерживающих Data Mining. Сегодня практически все коммерческие системы для работы с БД поддерживают основные алгоритмы Data Mining. Имеются и специализированные Data Mining-системы, как коммерческие, так и системы открытого доступа, ориентированные на излечение знаний из данных.
Целями данной работы являются рассмотрение и сравнительный анализ нескольких систем, позволяющих строить ассоциативные правила. Первые две системы – это популярные системы от крупных производителей:
– инструментарий фирмы Microsoft (Excel + SQL Server), позволяющий строить ассоциативные правила для данных, подготавливаемых в Excel и обрабатываемых затем в SQL Server;
– инструментарий arules, встроенный в RStudio, – инструментальную среду для программирования на языке R; пакет arules, разработанный Х. Борглетом [3], использует реализацию алгоритма Apriori на языке C.
Третья система – это система Ментор, разработанная авторами статьи. В ее основе лежит реализация на языке C# алгоритма Apriori, предложенная В. Биллигом [4].
Ассоциативные правила и алгоритм Apriori
Будем полагать, что мы имеем дело с объектами, где каждый объект vk характеризуется некоторым набором свойств Pk:
Pk = {pk, pk1, …, pkm}. (1)
Наборы Pk являются подмножествами общего для всех объектов множества свойств Properties:
Pk Í Properties = {p1, p2, …, pm}. (2)
Будем также полагать, что все свойства объектов являются бинарными. Это означает, что объект vk может либо обладать, либо не обладать свойством pj. Введем в рассмотрение БД dbp, содержащую интересующие нас наборы свойств объектов:
dbp = {P1, P2, …, PN}. (3)
Пусть X – некоторый набор свойств:
X = {pi1, pi2, …, piq}. (4)
Частоту набора или его поддержку в базе dbp будем определять как долю тех наборов БД, которые содержат набор X:
Support(X) = . (5)
Ассоциативным правилом Rule будем называть правило вида
X ® Y. (6)
Здесь X и Y – непересекающиеся наборы свойств:
X Ç Y = Æ. (7)
Важной характеристикой правила является его поддержка (support), которая определяется следующим образом:
Support(Rule) = Support(X ® Y) = Support(X È Y). (8)
Поддержка правила – это поддержка набора, включающего посылку и заключение правила. Правило Rule следует рассматривать как импликацию, правило вида «если то». Если в некотором наборе имеет место X, то предполагается, что в нем имеет место и Y. Другими словами, появление в наборе X с некоторой долей уверенности влечет появление Y. Для того чтобы правило имело практическую ценность, достоверность появления Y должна быть достаточно высокой.
Достоверность или уверенность (confidence) является второй важнейшей характеристикой правила, которая определяется как доля всех наборов БД, содержащих как X, так и Y, среди тех наборов, которые содержат X:
Confidence(Rule) = Confidence (X ® Y) = . (9)
Нетрудно заметить, что достоверность правила можно выразить через функцию поддержки Support:
Confidence(Rule) = Confidence (X ® Y) = . (10)
Еще одной важной характеристикой правила является параметр lift, задающий корреляцию между двумя событиями – появлением посылки правила и появлением заключения.
Обсудим роль этого параметра. Будем рассматривать параметр support, задающий частоту появления элемента в БД, как вероятность появления соответствующего события.
Тогда для правила A => B параметр lift определяется следующим образом:
(11)
Для независимых событий вероятность P(A, B) совместного появления событий A и B равна произведению вероятностей появления этих событий – P(A) * P(B), так что, параметр lift в этом случае равен 1. Для зависимых событий P(A, B) = P(A) * P(B/A), где условная вероятность P(B/A) – вероятность появления события B при условии, что произошло событие A, может быть значительно выше вероятности P(B). Для полностью зависимых событий, когда появление события A однозначно влечет появления события B, параметр lift получает максимальное значение: 1/P(B).
Возвращаясь к частотам, для правила A => B параметр lift определяется следующим образом:
. (12)
Заметьте, при расчете параметра lift по формуле (12) его значение может быть меньше 1, что свидетельствует об отрицательной корреляции – появление A уменьшает вероятность появления B.
Поскольку для правил A => B и B => A значения параметра lift совпадают, параметр lift характеризует не правило, а набор (A, B), задавая корреляцию между частями набора.
Для отображения корреляции между посылкой правила и его заключением вводят еще один параметр, называемый importance (важность правила).
В [8] важность определяется следующим образом:
Importance_1 = . (13)
В [9] важность определяется иначе:
Importance_2 = . (14)
Строгого определения этого параметра в документации [9] не дано, его описание можно перевести так: «Важность правила вычисляется как логарифм вероятности (правдоподобия) правой части правила при заданной левой части правила. Например, в правиле A => B вычисляется отношение случаев с A и B к случаям, когда появляется B, но не появляется A».
Соотношения (13) и (14) связаны следующим образом:
Importance_2 = Importance_1 + logP(A). (15)
Поскольку значение logP(A) не влияет на корреляцию посылки и заключения правила, а также учитывая, что определение, данное на сайте Microsoft, не является определением в строгом смысле этого понятия, далее под параметром «важность правила» будем полагать значение, определяемое соотношением (13).
Проведем анализ этого определения. Когда вероятность появления события B при условии, что произошло событие A, совпадает с вероятностью появления события B при условии, что событие A не произошло, значит, отсутствует всякая корреляция между событиями A и B. В этом случае отношение вероятностей равно 1, а логарифм этого отношения равен 0. Так что, значения параметра importance, близкие к 0, свидетельствуют об отсутствии корреляции между посылкой и заключением правила. Такие правила следует признать бесполезными даже в случае, если параметры support и confidence превосходят заданные минимальные значения.
Проанализируем другие крайние ситуации. Рассмотрим максимально возможную отрицательную корреляцию. Пусть обязательно должно появиться либо событие A, либо событие B. Если событие A не произошло, то событие B появится с вероятностью 1. В этой ситуации P(B/A) = 0, P (B/!A) = 1, отношение вероятностей равно 0, а логарифм этого отношения равен -∞. В другом крайнем случае положительной корреляции отношение вероятностей равно + ∞.
Анализ показывает, что параметр importance, рассчитываемый по формуле (13), может меняться в широких пределах. Переход к логарифмической шкале, конечно, сжимает интервал значений параметра, но не устраняет проблему полностью, особенно в случае жесткой корреляции.
Заметим, что реальные значения параметра importance, вычисляемые инструментарием Microsoft, не соответствуют формуле (13).
Следует также сказать, что терминология в этой области еще не сложилась окончательно. Так, параметр support принято называть поддержкой или частотой правила. Но часто, как это делали авторы статьи, этот параметр рассматривают как вероятность правила, учитывая ту объективную связь, которая существует между частотой появления события и его вероятностью.
Параметр confidence называют уверенностью или достоверностью правила. Но в инструментарии Microsoft этот параметр называют вероятностью правила. Параметр lift, характеризующий корреляцию между посылкой правила и его заключением, часто называют параметром corr (сокращение слова correlation).
О неопределенности в определении параметра importance, активно используемом в инструментарии Microsoft, уже говорилось. Понятно, что этот параметр учитывает, как и параметр lift, корреляцию между посылкой и заключением правила, но точный алгоритм вычисления этого параметра службами Microsoft Analysis Services авторам пока установить не удалось.
Цель алгоритма Apriori:
Найти все ассоциативные правила, у которых поддержка и достоверность выше заданных минимальных значений:
Rules = {Rule| Support(Rule) > support_min&Confidence(Rule) > confidence _min}.
Основная идея алгоритма Apriori
Идея, предложенная еще в работе [2], позволяет избавиться от полного перебора всех возможных наборов при построении ассоциативных правил. Суть идеи такова: назовем набор свойств X частым, если Support(X) > support_min. Справедливо следующее утверждение:
Если X – частый набор, то и все его подмножества являются частыми наборами.
Более важным является утверждение, следующее из отрицания этой импликации:
Если X не является частым набором, то и все его надмножества не являются частыми наборами.
Это свойство наборов, называемое антимонотонностью, при построении правил позволяет исключить из рассмотрения большое число наборов. Так, например, обнаружив, что некоторое свойство q редко появляется в наборах БД, можно не рассматривать все наборы БД, содержащие q.
Отсюда следует и общая схема реализации алгоритма Apriori. Вначале строится множество частых наборов F, содержащее наборы длины 1, и множество правил R, где посылка и заключение содержат наборы из F. Затем в цикле на основе уже построенных множеств частых наборов F и R длины k строится множества F и R длины k+1. Цикл завершается, когда не существует частых наборов длины k+1.
Свойство антимонотонности частых наборов лежит в основе всех известных реализаций построения ассоциативных правил.
Построение ассоциативных правил в системе Ментор
Разработанная авторами система Ментор является специализированной системой, ориентированной на построение ассоциативных правил. В ее основе лежит новая версия алгоритма Apriori, отличающаяся от известных нам реализаций этого алгоритма.
Две основные идеи лежат в основе модификации классического алгоритма Apriori: первая связана со способом представления данных, вторая носит более фундаментальный характер и связана со способом построения достоверных правил.
Представление данных в алгоритме Apriori_Scale
Как представлять записи БД? Естественный способ состоит в том, чтобы каждую запись рассматривать как переменную типа List, содержащую список свойств объекта.
Оценим при таком способе представления данных сложность функции Support(X), лежащей в основе всех вычислений. При расчете поддержки набора X необходимо в цикле по числу записей в БД определять, содержится ли список свойств набора X в списке, характеризующем k-ю запись Pk БД. Проверка вхождения данных одного списка в другой список требует O(M2) достаточно трудоемких операций. Общая сложность функции Support представима как O(N * M2), где N – число записей в БД, а M – число свойств.
В алгоритме Apriori_Scale авторы постарались избежать указанных трудностей. С этой целью для представления свойств объектов выбран тип Enumeration (перечисление). Особенностью этого типа является то, что внутреннее представление данных задается целыми числами, на которые отображаются элементы перечисления. Внешним же представлением данных, с которым работает пользователь, остаются строки текста, описывающие свойства объектов.
Более того, для представления данных выбран не просто тип Enumeration, а специальный вид этого типа, называемый шкалой. Шкала характеризуется тем, что k-й элемент перечисления отображается в число 2k. Такое представление позволяет для множества из M бинарных свойств установить взаимно однозначное соответствие между всевозможными наборами свойств и целыми числами из диапазона [0 – 2M+1 -1]. Это означает, что каждый элемент БД, задающий набор свойств, представляется одним целым числом. В двоичном представлении этого числа единица в k-м разряде говорит о том, что соответствующий объект обладает k-м свойством в перечислении. Подробности работы со шкалами даны в [7].
Представление данных перечислением, заданным шкалой, имеет немаловажную полезную особенность. Над элементами перечисления определены логические побитовые операции. Это позволяет крайне эффективно решать базовую для алгоритма операцию – определение вхождения элементов одного множества в другое множество. Пусть X – заданный набор свойств, а Pk – элемент БД. Объекты X и Pk принадлежат типу Enumeration, заданному шкалой. Тогда для установления того, что X Í Pk, достаточно вычислить следующее булевское выражение:
(X & Pk) = X. (16)
В этом выражении & – побитовая конъюнкция, выполняемая над двоичными представлениями X и Pk. Также будем использовать знак операции | для логической побитовой операции дизъюнкции. Операции & и | можно рассматривать и как операции пересечения и объединения соответствующих множеств.
Выбранное представление позволяет сложную операцию определения вхождения множества X в множество Y выполнять за константное время, не зависящее от размера множеств, практически мгновенно, поскольку для выполнения требуются две машинные операции компьютера. Отсюда существенно упрощается сложность вычисления функции Support. При выбранном представлении сложность вычисления этой функции O(N) линейно зависит от размера БД с минимальной константой.
Итеративный расчет достоверных ассоциативных правил
Уже отмечалось, что основная идея алгоритма Apriori связана с итеративной схемой построения частых наборов. Частые наборы длины k строятся на основе частых наборов длины k–1 и единичных частых наборов. Нечастые наборы в построении правил не участвуют. В этом суть алгоритма Apriori.
В алгоритме Apriori Scale, помимо свойства антимонотонности, характеризующего частые наборы, используется похожее свойство, характеризующее достоверные правила. Это свойство позволяет строить достоверные правила на шаге k на основании достоверных правил, построенных на шаге k–1. В основе алгоритма лежит следующее утверждение:
Если X => Yk достоверное правило, то достоверным является и любое правило X =>Yj с той же посылкой X и заключением Yj , представляющим собственное подмножество Yk .
Докажем справедливость этого утверждения.
Так как Yj – собственное подмножество Yk, то Yk можно представить в виде Yk = Yj | add. Эта запись учитывает, что переменные заданы перечислением, так что, объединение множеств выразимо через операцию дизъюнкции.
Достоверность правила X => Yk вычисляется следующим образом:
Q(X ® Yk) = . (17)
Достоверность правила X => Yj вычисляется следующим образом:
Q(X ® Yj) = . (18)
Знаменатели в формулах (17) и (18) совпадают, а числитель в формуле (17) по свойству частоты множеств меньше или равен числителю в формуле (18). Отсюда следует справедливость нашего утверждения.
Следствие
Из отрицания доказанного утверждения следует справедливость утверждения:
Если правило X => Yj недостоверно, то недостоверно и правило X => Yk.
Свойство антимонотонности имеет место не только для частых наборов, но и для достоверных правил. Отсюда следует, что достоверные правила с заданной посылкой X можно строить на основе ранее построенных достоверных правил с той же посылкой.
Заметим, что утверждение касается только правил с заданной посылкой. Возможна ситуация, когда правила X => Y и Z => Y недостоверны, а правило X | Z => Y достоверно. Поэтому недостаточно построить достоверные правила на шаге k, используя только достоверные правила шага k–1. К этому множеству правил достаточно добавить достоверные правила, посылка которых выбирается из множества частых правил длины k, а заключение является частым единичным набором.
Отсюда следует схема алгоритма Apriori_Scale. Вначале строится множество частых достоверных правил с единичной посылкой и заключением. Далее итеративно уже построенное множество достоверных частых правил на шаге k–1 расширяется. Затем к этому множеству добавляются достоверные правила, посылка которых выбирается из множества частых правил длины k, а заключение является частым единичным набором. Процесс продолжается, пока можно строить новые правила.
Рассмотрим, как происходит расширение множества достоверных правил на каждом шаге.
Пусть на шаге k–1 построено частое достоверное правило X => Y.
Пусть cand – частый единичный набор. Тогда данное правило позволяет породить четыре правила:
X | cand => Y; Y => X | cand; X => Y | cand; Y | cand => X.
Заметим, все эти правила имеют одинаковую поддержку – Support(X | Y | cand). Так что, если значение поддержки меньше минимального значения, то ни один из четырех кандидатов не включается в список правил следующего шага. Для подсчета достоверности правил достаточно вычислить два значения функции Support: Support(X | cand) и Support(Y | cand).
Теорема
Алгоритм Apriori Scale строит все частые достоверные правила.
Доказательство этого утверждения по сути приведено выше.
Итоги
Подводя промежуточные итоги, отметим, что алгоритм Apriori Scale позволяет:
– существенно упростить и сократить объем БД; БД из N записей может быть представлена файлом из N целых чисел;
– для пользователя программы сохраняется естественное для данной проблемной области описание свойств рассматриваемых объектов;
– вычисление базисной для алгоритма функции Support может быть выполнено за линейное время, пропорциональное размеру БД и не зависящее от числа исследуемых свойств;
– в отличие от классического алгоритма Apriori, учитывающего только свойство антимонотонности частых множеств, в алгоритме учитывается свойство антимонотонности достоверных правил, позволяющее строить достоверные правила на основе ранее построенных достоверных правил меньшего размера.
Ограничения алгоритма и их преодоление
Рассмотрим ограничения, присущие алгоритму AprioriScale, и возможные способы их преодоления.
Количественные свойства
В алгоритме Apriori_Scale, как и в алгоритме Apriori, предполагается, что все свойства носят бинарный характер: свойство либо наличествует у объекта, либо нет. В то же время на практике свойство может быть представлено числом из некоторого диапазона. Примеров можно привести сколь угодно много, например, температура или давление, измеряемое у пациента, цена товара, длина запроса. Как поступить в таких случаях?
Нужно понимать, что ассоциативные правила носят качественный, а не количественный характер. Поэтому для правил точные значения измеряемых параметров чаще всего не столь важны. В большинстве ситуаций достаточно разбить диапазон возможных значений параметра на несколько непересекающихся интервалов, обычно не более пяти. Например, при разбиении на три интервала каждому интервалу можно поставить в соответствие три свойства: норма, ниже нормы, выше нормы. В общем случае такой подход позволяет каждый количественный параметр заменить k бинарными свойствами, где k – число разбиений диапазона возможных значений исходного параметра. Следует заметить, что свойства «норма» или «ниже нормы» носят качественный характер и для ассоциативных правил более важны, чем знание количественных значений.
Число свойств
Важной особенностью алгоритма Apriori Scale является то, что набор свойств объекта имеет тип перечисления, представленного шкалой. Это означает, что каждому свойству ставится в соответствие число 2 в степени k. Отсюда следует, что максимальное число свойств не должно быть больше шестидесяти трех; поскольку стандартное перечисление при программировании на C# необходимо проецировать на целочисленный тип, максимальную возможность дает проецирование на тип long.
Можно заметить, что для исследователя, занимающегося анализом ассоциативных правил, 60 – это большое число. Так что, вряд ли при построении правил следует вводить более 60 свойств. Тем не менее, если такая задача возникает, то существует разработанная авторами данной работы модификация алгоритма. В этой модификации вместо стандартного класса enum используется собственный класс longenum, задающий перечисление, в котором нет ограничения на длину перечисления при сохранении всех достоинств работы с перечислениями.
Реализация алгоритма Apriori Scale на языке C#
Рассмотрим ключевые моменты реализации алгоритма на языке программирования C#.
Задание перечисления
Класс Properties для тестового примера представляет перечисление элементов, заданное шкалой. Вот его описание:
[Flags]
public enum Properties : long
{
I1 = 1L << 0, I2 = 1L << 1, I3 = 1L << 2, I4 = 1L << 3, I5 = 1L << 4
}
В данном перечислении заданы пять факторов. Атрибут класса [Flags] и указание для каждого фактора числа, задающего внутреннее представление фактора, показывает, что перечисление является шкалой. Запись 1L ≪ k является C# аналогом математической записи 2k, где значение 2k принадлежит типу long. Операция << в C# является операцией сдвига влево на k разрядов, что и дает число 2k типа long.
Построение правил
Основной метод, строящий правила, достаточно прост, так что, можно привести его полную реализацию:
/// <summary>
/// Создание списка правил
/// Основной метод
/// </summary>
public void Create_Rules()
{
Create_Rules_1();
bool exist_new_rules = true;
while(exist_new_rules)
{
exist_new_rules = Create_Rules_K();
}
}
Вначале создается список достоверных правил, где посылка и заключение имеют длину 1, то есть содержат по одному элементу. Затем в цикле по уже построенным правилам и множеству частых примеров длины k–1 строятся правила длины k, когда на 1 расширяется длина посылки и/или заключения. Процесс построения заканчивается, когда новые правила построить не удается.
Функция Support
Как уже отмечалось, функция Support при данном выборе представления данных имеет линейную сложность и вычисляется просто. Вот ее текст:
/// <summary>
/// Поддержка объекта в базе данных
/// </summary>
/// <param name="bask">объект, для набора свойств которого
/// вычисляется поддержка (частота появления в базе данных) </param>
/// <returns> частота появления набора </returns>
public double Support(Bask bask)
{
double count = 0;
foreach (Bask item in db)
{
if ((bask.Bask_prop & item.Bask_prop) == bask.Bask_prop)
count++;
}
return count / n;
}
В цикле по записям БД счетчик count увеличивается на единицу, если все свойства объекта bask содержатся в записи БД. Выражение if построено в полном соответствии с выражением (16).
Построение частых наборов и правил длины 1
Метод Create_Rules_1, строящий список частых примеров и достоверных правил длины 1, достаточно прост и понятен. Его реализация очевидна, так что нет необходимости приводить его полный текст. Достаточно лишь упомянуть, что редкие одиночные свойства и недостоверные правила в соответствии с принципом антимонотонности в дальнейшем рассмотрении участвовать не будут.
Построение частых наборов и достоверных правил длины k
Метод Create_Rules_k, строящий достоверные правила длины k, является центральным методом в реализации алгоритма. Его основные идеи достаточно подробно описаны. Приводить его полную реализацию на языке программирования здесь не имеет смысла.
Инструментарий системы Ментор
При создании программного инструментария главной задачей являлось построение на основе алгоритма Apriori Scale достоверных ассоциативных правил, извлекаемых из БД. Не менее важным являлось создание средств, удобных для проведения анализа правил, выбор из множества правил тех, которые несут содержательный смысл и позволяют отвечать на поставленные исследователем вопросы.
Основная форма построения правил
На рисунке 1 показана форма, позволяющая создавать правила на основе выбранной БД и граничных характеристик частоты и достоверности правил.
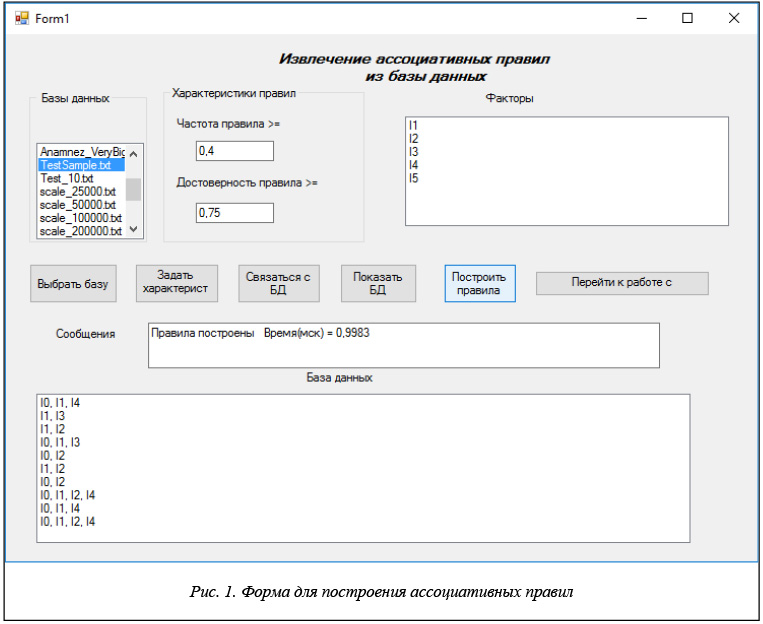
Элемент управления ListBox «Факторы» содержит cписок анализируемых свойств.
Элемент управления ListBox «Базы данных» содержит список БД, которые могут использоваться для построения правил.
Два текстовых поля «Частота правил» и «Качество (достоверность) правил» содержат минимальные значения частоты и качества правила, ниже которых правила не строятся.
Ряд командных кнопок позволяют пользователю выполнять различные действия, необходимые для построения правил.
Выбрав из списка БД и нажав кнопку «Выбрать базу», получаем имя БД, с которой будем работать, и путь к соответствующему файлу, хранящему БД.
Задав в текстовых полях значения минимальной частоты и минимального качества и нажав кнопку «Задать характеристики», получаем характеристики правил, которые будут использоваться при построении правил.
Нажатие кнопки «Связаться с БД» приводит к открытию соответствующей БД.
Нажатие кнопки «Показать БД» приводит к отображению соответствующей БД в элементе управления ListBox «База данных».
Предполагается, что командные кнопки нажимаются в указанном порядке. Если БД открыта, характеристики правил заданы, то при нажатии кнопки «Построить правила» строятся ассоциативные правила, частота и достоверность которых выше заданных минимальных характеристик.
Последняя в ряду командная кнопка «Перейти к работе с правилами» открывает новую форму.
Важную роль играет текстовое окно «Сообщение». При нажатии каждой командной кнопки в этом окне появляется информация о результатах выполнения действия, заданного командной кнопкой. Если действие выполнено в соответствии со спецификациями, то сообщение подтверждает успешность выполнения действия. Так, на рисунке 1 показано, что после нажатия командной кнопки «Построить правила» в окне «Сообщение» отображается текст, уведомляющий, что правила успешно построены и на их построение потребовалось 5 микросекунд времени. Если же по каким-либо причинам действие выполнить не удалось, то в окне появляется сообщение, указывающее причину, по которой не удалось выполнить действие. Например, если пользователь нажал кнопку «Выбрать базу», не выбрав предварительно базу в списке БД, то появится сообщение «Выберите из списка имя базы данных, после чего нажмите кнопку <Выбрать базу>».
Форма для работы с построенными правилами
После того как в основной форме построены правила и нажата командная кнопка «Перейти к работе с правилами», открывается новая форма, позволяющая выполнять некоторые действия над правилами.
Основная операция, выполняемая на этом этапе, это фильтрация правил. Алгоритм чаще всего строит правила, лишь часть из которых интересуют исследователя при решении его специфических задач. Поэтому возникает необходимость фильтрации правил. Конечно, фильтр можно было бы задавать еще на этапе построения правил, но это осложнило бы алгоритм построения. Учитывая, что правила строятся быстро, удобнее иметь возможность задавать фильтр для уже построенного полного множества правил.
На рисунке 2 показана форма для работы с построенными правилами.
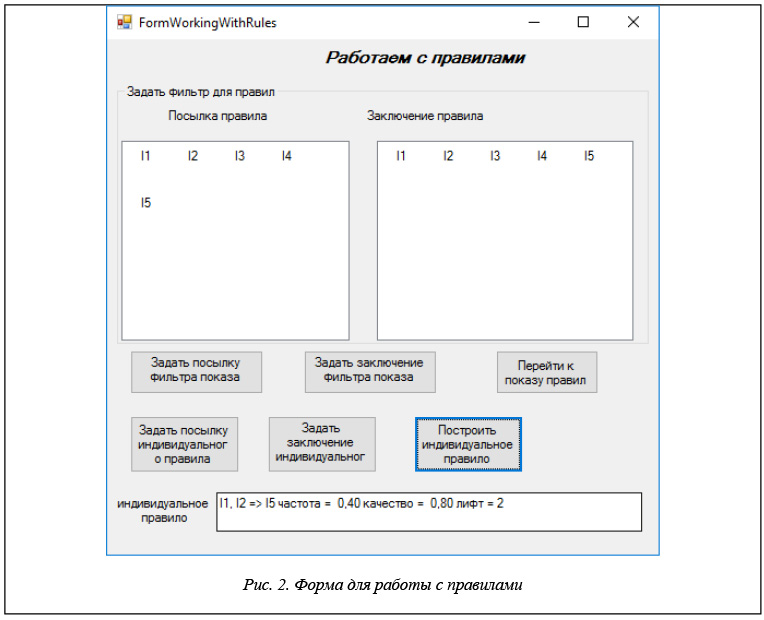
Два элемента управления ListView отображают в нескольких столбцах все исследуемые свойства.
В каждом из них можно выбрать ряд свойств. В элементе управления «Посылка правила» задаются свойства, накладываемые фильтром на посылку правила. Фильтр из всех правил будет отбирать лишь те правила, свойства которых содержатся в свойствах, заданных фильтром. Аналогично в элементе управления «Заключение правила» можно выбрать свойства, которые будут включаться в заключение правила.
Выбрав свойства в «Посылке правила» и нажав командную кнопку «Задать посылку фильтра показа», задаем первую часть фильтра – фильтр посылки правил. Аналогично, выбрав свойства в «Заключении правила» и нажав командную кнопку «Задать заключение фильтра показа», задаем вторую часть фильтра – фильтр заключения правила. После этого можно перейти к показу отфильтрованных правил, нажав командную кнопку «Перейти к показу правил».
Еще одна полезная возможность, предоставляемая этим инструментом, состоит в том, что исследователя может интересовать некоторое конкретное правило. Используя те же элементы управления «Посылка правила» и «Заключение правила», можно выбрать те свойства, которые будут включены в посылку и заключение конкретного правила. Командные кнопки «Задать посылку индивидуального правила»
и «Задать заключение индивидуального правила» выполняют указанные действия. Командная кнопка «Построить индивидуальное правило» строит правило с заданной посылкой и заключением, рассчитывает его характеристики – частоту и достоверность и выводит результаты в текстовое окно «индивидуальное правило». На рисунке 2 показан результат построения одного из таких правил.
Форма показа правил
На рисунке 3 показана форма завершающего этапа работы с правилами.
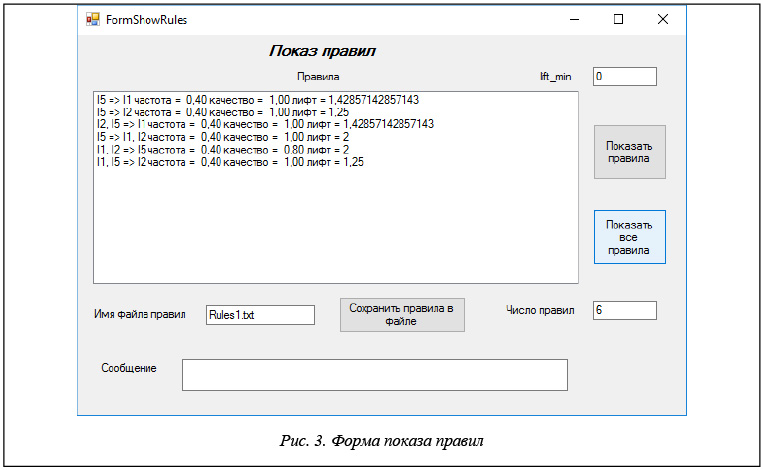
Нажав командную кнопку «Показать правила», в списке «Правила» можно видеть все правила, соответствующие фильтру, построенному на предыдущем этапе. Командная кнопка «Показать все правила» позволяет просмотреть полный список построенных ассоциативных правил без учета фильтрации.
Показанные правила можно отфильтровать по параметру lift, задав его минимальное значение в соответствующем окне формы. На рисунке 4 показаны отфильтрованные правила.
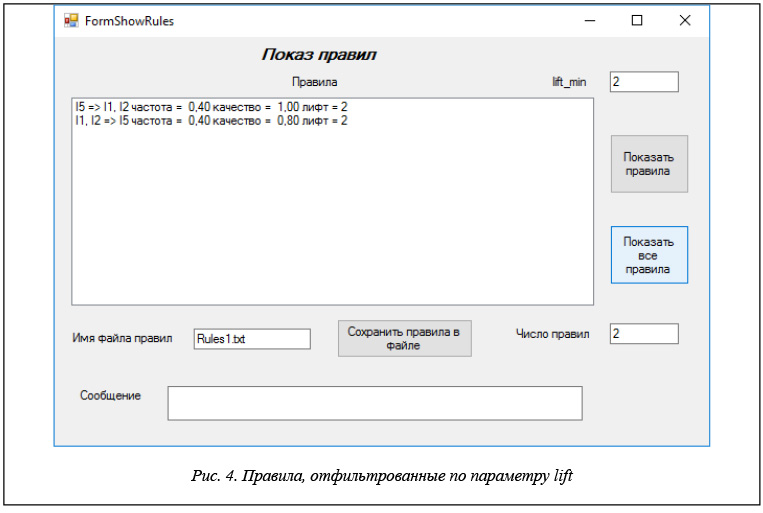
Правила, отображаемые в окне списка, можно сохранить в файле, имя которого указывается в соответствующем текстовом окне. Результат выполнения этой операции и полный путь к файлу показываются в окне «Сообщение».
На рисунке 5 показан сохраненный файл из шести правил, открытый в блокноте.
Язык R, RStudio и инструментарий «ARules» построения ассоциативных правил
Язык R – предметно-ориентированный язык, предназначенный для статистической обработки данных и работы с графикой. Его авторами являются Росс Айхэка и Роберт Джентлмен. Язык назван по первой букве имен авторов. Разработан в университете Окленда в Австралии в 1993 году [5].
Одним из важных достоинств языка, сделавших его весьма популярным не только в предметной области, связанной со статистической обработкой данных, но и как универсального языка программирования, явился способ расширения возможностей языка за счет включения специализированных пакетов.
В настоящее время число пакетов достигает нескольких тысяч. Существует множество реализаций языка R, включенных в различные среды разработки, начиная от MatLab, OracleDatabase и кончая реализацией от фирмы Microsoft.
Язык R и дополнительные пакеты, не вошедшие в основную поставку, распространяются через CRAN (Comprehensive R ArchiveNetwork) [6].
RStudio – среда разработки программ на языке R с графическим интерфейсом. Все примеры на R, появляющиеся в данной статье, построены в этой среде.
Пакет arules поддерживает построение ассоциативных правил.
Структура пакета arules
На рисунке 6 представлены классы, входящие в пакет arules, и их взаимосвязи.
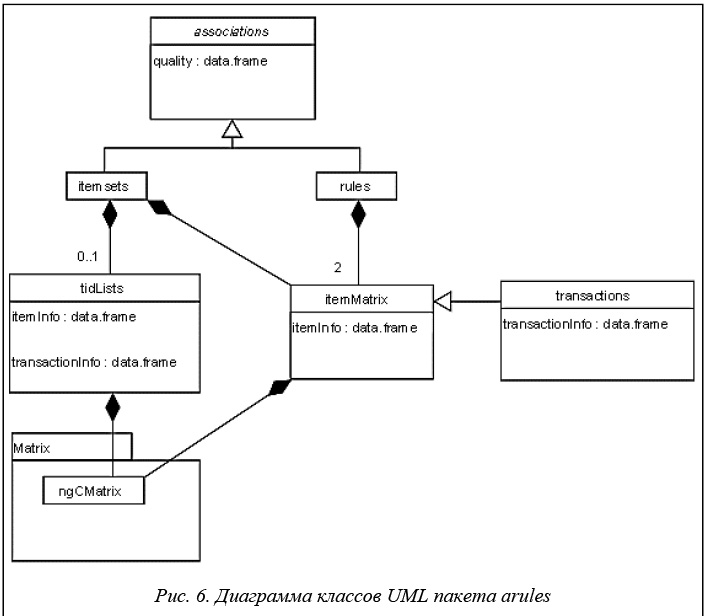
Отношение наследования (отношение is – является) между классами показано на рисунке 7.
В этом случае говорят, что класс transactions является наследником класса itemMatrix или класс transactions расширяет класс itemMatrix.
Отношение композиции (отношение has – имеет) показано на рисунке 8.
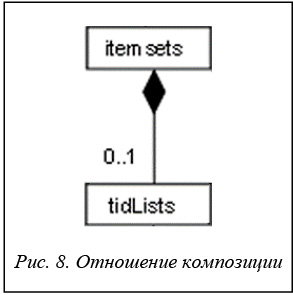
В этом случае говорят, что класс itemSets может содержать в себе от 0 до 1 экземпляра класса tidLists. Композиция имеет жесткую зависимость времени существования экземпляров класса контейнера и экземпляров содержащихся классов. Если контейнер будет уничтожен, то все его содержимое также будет уничтожено.
Входные данные представлены классами transactions и tidLists (списки идентификаторов транзакций как альтернативный способ представления данных транзакций). Эти классы хранят ассоциативные правила в горизонтальном (transactions) или вертикальном (tidLists) виде. На рисунке 9 показана небольшая база данных покупок в магазине в этих двух видах.
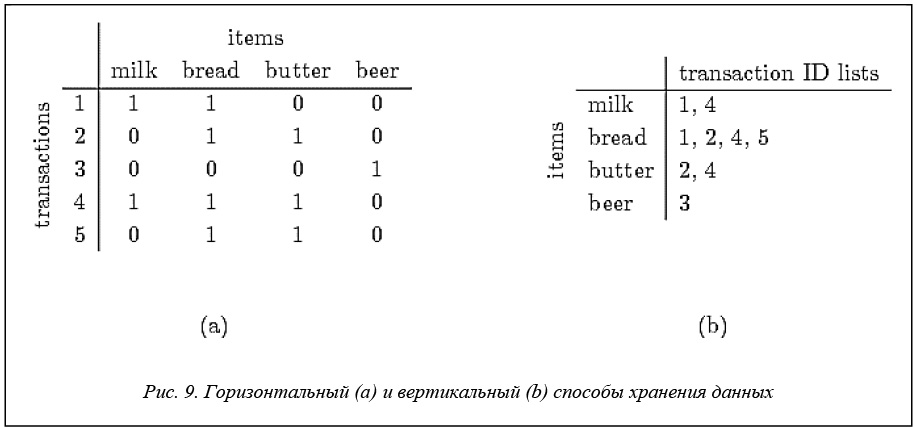
Выходными данными пакета являются классы itemsets и rules, представляющие соответственно наборы элементов и правил. Оба класса расширяют виртуальный класс associations, обеспечивающий общий интерфейс. Данная структура позволяет легко добавлять новые алгоритмы поиска ассоциативных правил путем добавления нового класса, расширяющего associations.
Элементы в классах associations и transactions реализованы классом itemMatrix, который обеспечивает необходимую реализацию класса разреженной матрицы ngCMatrix из пакета R Matrix. Наборы элементов, используемые для БД транзакций и наборов ассоциаций, можно представить в виде двоичной матрицы инцидентности, где колонки соответствуют элементам, а строки – наборам. Двоичные элементы матрицы говорят о наличии (1) или отсутствии (0) элемента в наборе.
Реализация алгоритма построения ассоциативных правил в пакете arules
Как уже отмечалось, в пакете arules используется алгоритм, разработанный Христианом Борглетом на языке C. Псевдокод алгоритма представлен на рисунке 10.
Этот псевдокод приводит сам Борглет, предваряя полное описание алгоритма на С. Судя по псевдокоду, реализация основывается на предварительном генерировании множества кандидатов на частые наборы, не используя такие приемы, как сжатие исходной БД в виде FP-дерева частых наборов. Построенная реализация весьма эффективна, что будет продемонстрировано на примерах работы с большими БД. Она достаточно сложна, но доступна для изучения на сайте Борглета [3]. Исследования показывают, что реализация фактически использует предварительное сжатие БД и построение структуры данных, позволяющей эффективно определять систему правил. В результате время нахождения правил практически не зависит от задаваемых характеристик частоты и достоверности правил.
Работа с БД в RStudio
Язык R поддерживает работу с самыми разнообразными форматами данных. Данные могут храниться в реляционной базе (PostgreSql, MySql и др.), в файле Excel, приниматься удаленно от сервера.
Для тестирования данного алгоритма все БД хранились в .csv файлах. CSV (от англ. Comma-Separated Values – значения, разделенные запятыми) – текстовый формат, предназначенный для представления табличных данных. Каждая строка файла – это одна строка таблицы. Значения отдельных колонок отделяются разделительным символом (delimiter) – запятой (,). Однако большинство программ вольно трактуют стандарт CSV и допускают использование иных символов в качестве разделителя. В частности, в русскоязычных ОС, где десятичным разделителем является запятая, в качестве табличного разделителя, как правило, используется точка с запятой. Значения, содержащие зарезервированные символы (двойная кавычка, запятая, точка с запятой, новая строка), обрамляются двойными кавычками ("); если в значении встречаются кавычки, они представляются в файле в виде двух кавычек подряд. Строки разделяются парой символов CR LF (0x0D 0x0A) (в DOS и Windows эта пара генерируется нажатием клавиши Enter). Однако конкретные реализации могут использовать другие общепринятые разделители строк, например LF (0x0A) в UNIX.
Этот формат является наиболее простым и удобным для использования.
Тестовый пример
Дальнейшее рассмотрение ведется на тестовом примере, в котором БД содержит 10 транзакций (объектов). Каждая транзакция задается подмножеством элементов (бинарных свойств) из полного множества, включающего 5 свойств. БД тестового примера (в горизонтальном представлении) показана на рисунке 11.
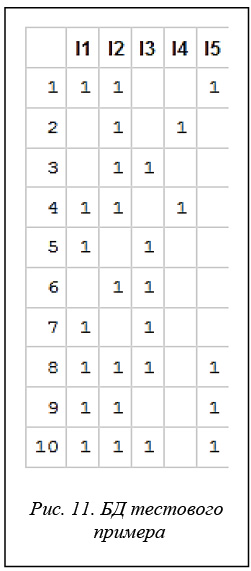Построение ассоциативных правил в RStudio
Для построения ассоциативных правил в RStudio авторами при помощи пакета shiny разработано приложение «Анализ данных».
Shiny – пакет RStudio, предназначенный для создания интерактивных веб-приложений на базе R.
В простейшем виде приложение, созданное при помощи Shiny, состоит из двух файлов, которые хранятся в одной папке. Один из этих обязательных файлов с фиксированным именем ui.R содержит определения элементов пользовательского интерфейса; второй – с именем server.R – содержит скрипт, определяющий работу сервера.
Важными концепциями, реализованными в пакете Shiny, являются следующие:
– входные данные хранятся в объекте input, выходные – в объекте output; извлечение необходимых данных выполняется обычным для R способом – при помощи оператора $;
– объект с данными, над которыми выполняются вычисления, инициализируется в момент запуска приложения;
– для обновления выводимой на экран информации в реальном времени используются «реактивные» функции (функции, мгновенно реагирующие на выполненные пользователем изменения тех или иных параметров).
На рисунке 12 показана первая форма приложения, позволяющая выбрать нужный набор данных или загрузить свой набор. Все данные представлены в виде .csv файлов. Также присутствуют различные способы настройки отображения выбранной базы (элементы «Разделитель», «Кавычки» и «Заголовки»). Элемент «Квантование» предоставляет возможность разбиения численных переменных базы на категории.
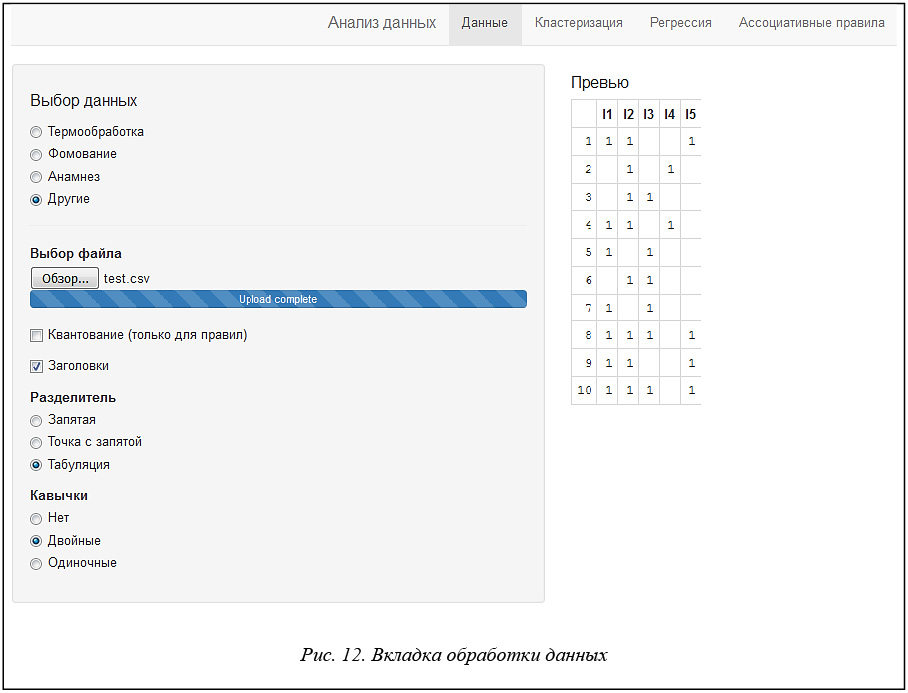
Выбрав и настроив нужную БД, можно переходить к вкладке «Ассоциативные правила», представленной на рисунке 13.
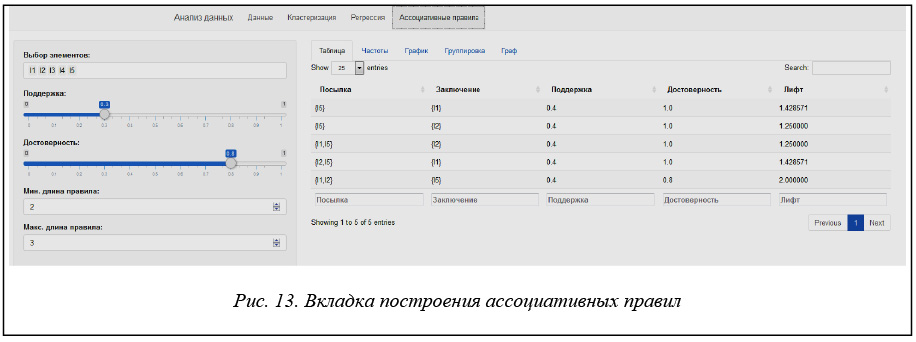
На данной вкладке производится основная работа по нахождению ассоциативных правил. Приложения пытаются автоматически построить правила при переходе на эту вкладку. При этом используются параметры по умолчанию. В левой части вкладки производится выбор настроек правил. Настройки будут подробно описаны в следующем разделе. В правой части представлено несколько способов отображения построенных правил.
На внутренней вкладке «Таблица» правила представлены в виде таблицы, в которой показываются найденные правила, их поддержка, достоверность и лифт.
Видим, что из тестовой базы было извлечено 5 правил при минимально допустимой поддержке 0,3 и минимально допустимой достоверности 0,8. При изменении этих параметров количество найденных правил будет меняться.
Извлечение из БД правил, имеющих высокую достоверность (0,8 и выше), позволяет обнаружить существование сильных ассоциативных связей между элементами I1, I2 и I5.
Наряду с построением ассоциативных правил система позволяет визуализировать закономерности, присущие данным.
Графическое представление в R закономерностей, присущих данным
Известно, что, как правило, картинка информативнее текста. Поэтому в R большое внимание уделяется графическому представлению анализируемых данных. К сожалению, для ассоциативных правил эффект графического представления не столь значителен из-за многомерности данных. Ассоциативное правило, представляющее интерес, многомерно. Такое правило, извлекаемое из данных, устанавливает тот факт, что некоторая совокупность факторов влечет появление определенного фактора или группы факторов. Отображать графически связи в многомерном пространстве факторов достаточно трудно, теряется эффект визуализации.
На внутренней вкладке «Частоты» (рис. 14) отображается частота появления в базе отдельных факторов.
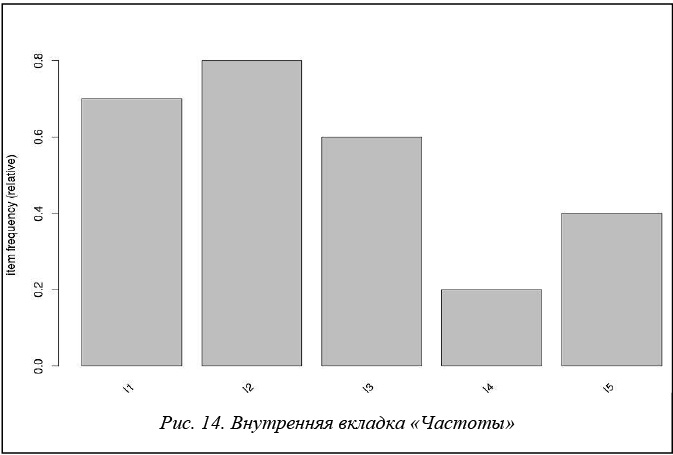
Информация о частотах отдельных факторов в графическом виде полезна, но становится проблематичной при большом числе факторов.
На внутренней вкладке «График» (рис. 15) показана возможность отображения множества построенных правил в пространстве параметров, характеризующих правило: поддержка, достоверность и лифт.
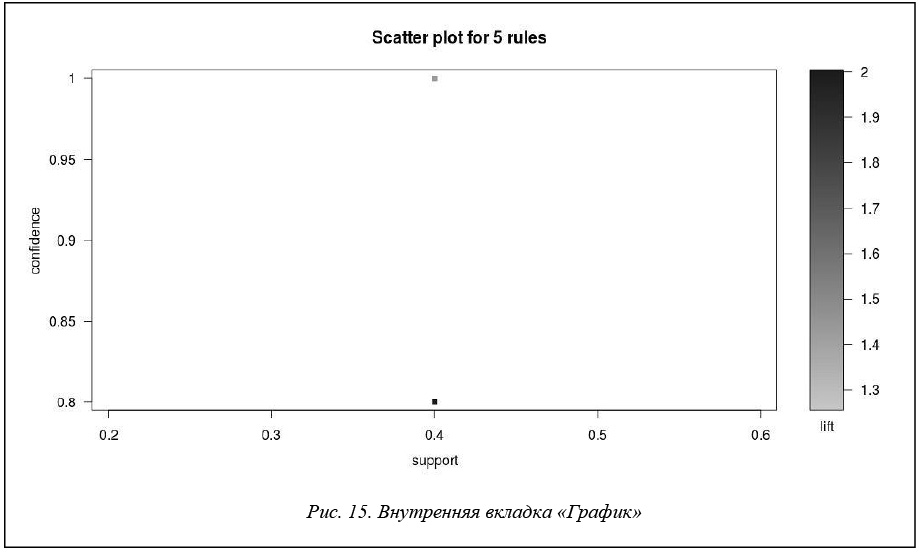
Первые два параметра, support и confidence, играют роль координатных осей плоскости.
Лифт задает степень затененности точки плоскости, в которую отображается правило. N построенных правил отображаются в M точек плоскости, где M <= N, позволяя наглядно видеть на графике существование правил с высокой частотой, достоверностью и корреляцией.
Для нашего примера тестовой БД пять построенных правил отображаются на графике двумя точками. Все построенные правила имеют одинаковую поддержку – 0,4 и два значения достоверности – 0,8 и 1, так что, четыре построенных правила отображаются в одну точку с координатами 0,4 и 1, а одно правило – в точку с координатами 0,4 и 0,8.
Точке с координатами 0,4 и 0,8 соответствует правило I1, I2 => I5, у которого значение параметра lift максимально и равно 2, так что, соответствующая точка выглядит более яркой.
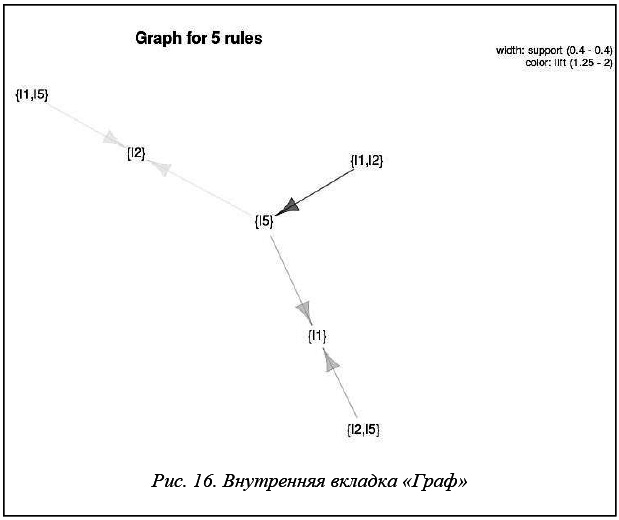
Внутренняя вкладка «Граф» (рис. 16) показывает отношения между посылкой и заключением правил в виде графа. Направление стрелки указывает на заключение правила, толщина – на поддержку, а цвет – на лифт.
Настройки и управление построением правил в RStudio
Все настройки алгоритма добычи ассоциативных правил представлены на рисунке 17.
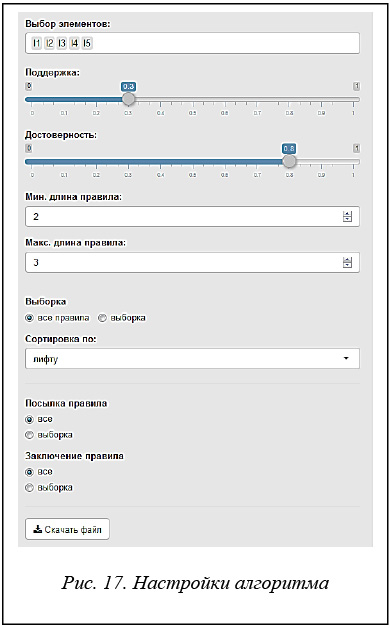
Слайдеры «поддержка» и «достоверность» регулируют минимально допустимый предел поддержки и достоверности найденных ассоциативных правил. Правила ниже этого предела исключаются.
Элементы «Мин. длина правила» и «Макс. длина правила» регулируют количество элементов в найденных правилах (посылка плюс заключение). Правила, не удовлетворяющие
этому условию, исключаются.
Элементы «Выборка» и «Сортировка по:» служат для настройки графиков на внутренних вкладках «График», «Группировка» и «Граф». Если количество найденных правил слишком велико, эти элементы позволяют отфильтровать и отсортировать результаты.
Элементы «Посылка правила» и «Заключение правила» позволяют искать правила, содержащие только заданные посылки и заключения. При нажатии на кнопку «Выборка» под соответствующим элементом появится меню для выбора необходимых переменных из БД.
Инструментарий Microsoft построения ассоциативных правил
Начиная с версии 2005, Microsoft SQL Server предоставляет интегрированную среду для обработки больших массивов данных. Среда SQL Server включает в себя службу Analysis Services, созданную для интеллектуального анализа данных, – набор алгоритмов Data Mining.
Для удобства пользователей разработан сервис Data Mining Client как надстройка к MS Excel, позволяющий обрабатывать данные, представленные таблицей MS Excel. Данные передаются из Excel в SQL Server, где и обрабатываются сервисами Analysis Services [10].
Архитектура обмена данными показана на рисунке 18.
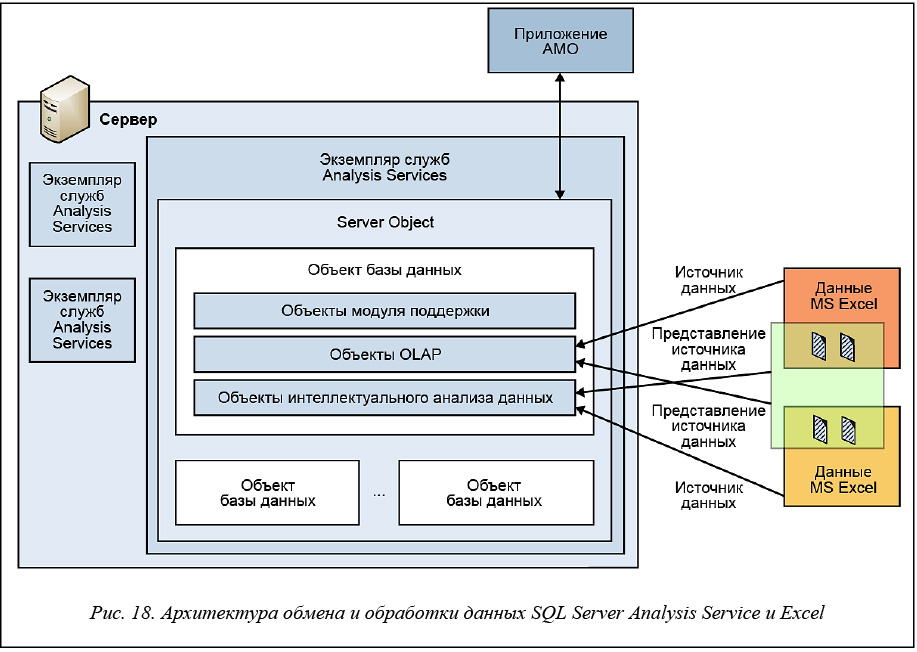
Сервер представляет собой изолированную службу Microsoft Windows и обменивается данными с клиентами. В роли клиента выступает надстройка интеллектуального анализа данных для MS Excel.
Прослойкой между пользовательским приложением и экземпляром служб Analysis Services является служба Analysis Management Objects (AMO) – библиотека классов, которая отвечает за взаимодействие клиента и сервера и помогает управлять службой SQL Server Analysis Service и размещенными в ней БД через пространство имен Microsoft.AnalysisServices [11].
Иерархия основных классов библиотеки приведена на рисунке 19.
Служба AMO позволяет создавать, редактировать и удалять экземпляры моделей, которые создаются в клиенте SQL Analysis Services. Доступ к библиотеке можно получить в среде MS Visual Studio, указав в проекте ссылку на данную сборку.
Как установить требуемый инструментарий
Для построения ассоциативных правил с помощью инструментария Microsoft необходимо на компьютере иметь установленное приложение Excel. В этом случае можно установить свободно распространяемую надстройку Data Mining Add-ins for Excel, отметив в мастере настройки приложения пункты «Средства анализа таблиц Excel» и «Клиент интеллектуального анализа данных для Excel» (рис. 20).
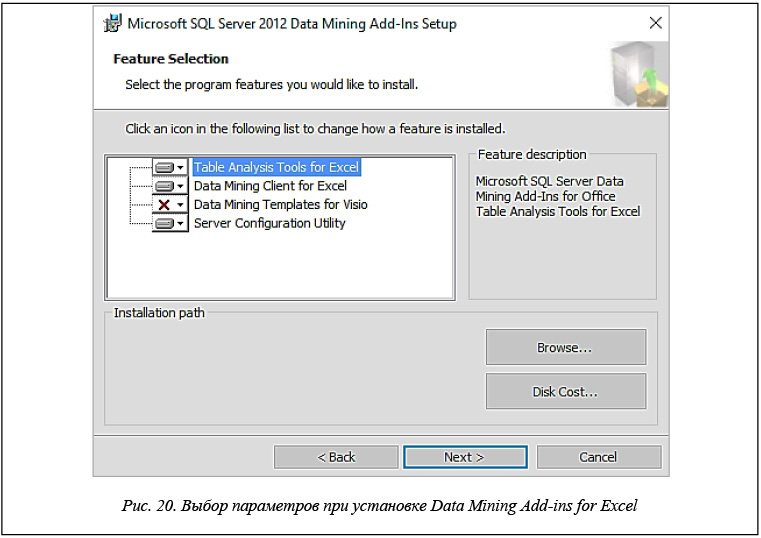
При открытии приложения MS Excel после установки надстроек мастер настройки автоматически запускает следующее окно, представленное на рисунке 21.
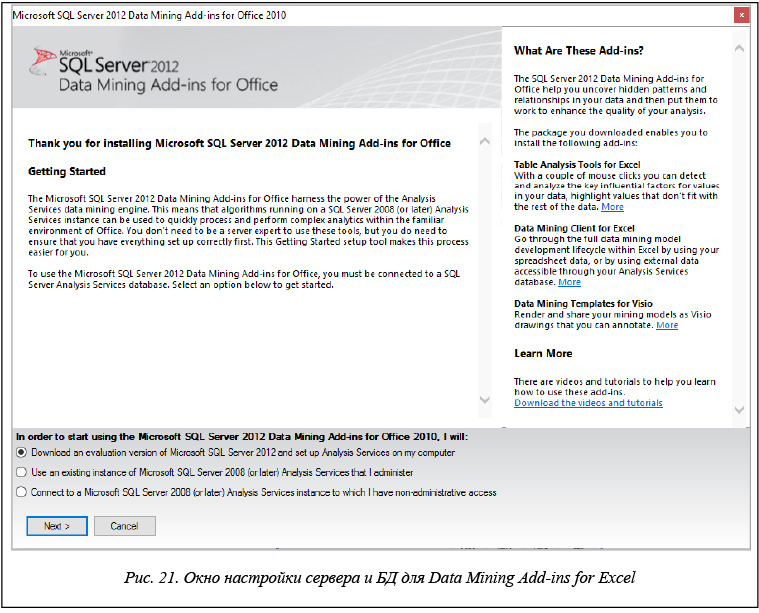
Для установки необходимо выбрать SQL-сервер, с которым будет работать клиент. При отсутствии установленного SQL Server Enterprise на компьютере мастер настройки предложит установить демо-версию сервиса с сайта Microsoft или выбрать установочный диск с программой. Необходимо отметить, что надстройка Data Mining Add-ins for Excel работает только с версией сервера Enterprise.
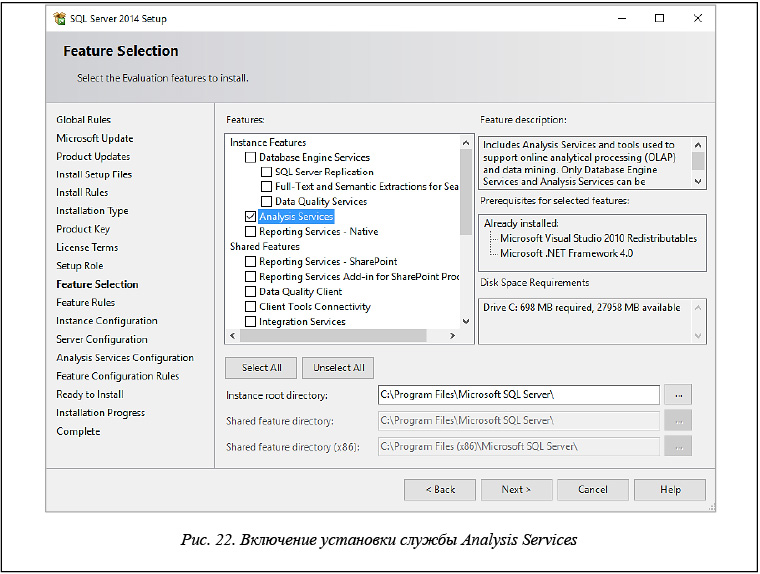
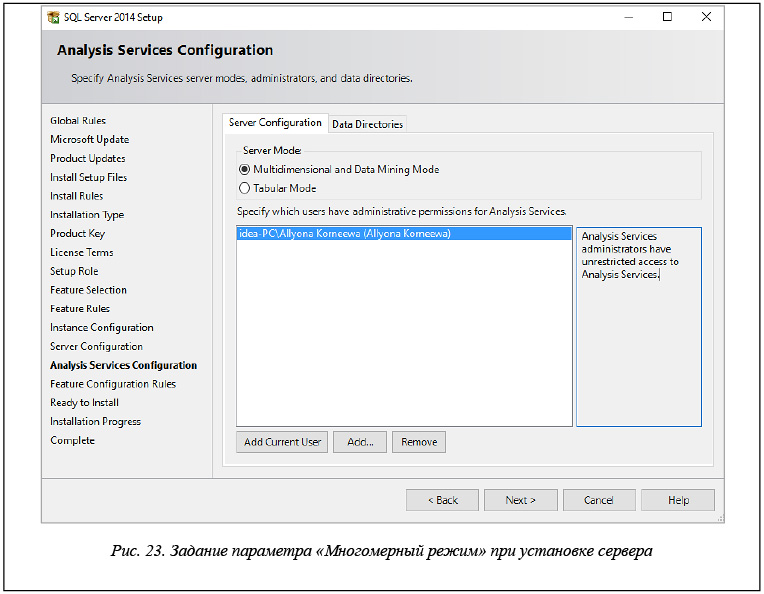
При установке сервера требуется отметить необходимость установки компонента Analysis Services (рис. 22) и создать экземпляр служб Analysis Services, работающий в многомерном режиме (табличный режим не поддерживает интеллектуальный анализ данных) (рис. 23).
После выбора сервера будет произведена настройка подключения клиента Excel и сервера. В ходе настройки рекомендуется создать новую БД на сервере для хранения моделей интеллектуального анализа данных и разрешить клиенту создание временных моделей. Временные модели, или «модели сеанса», хранятся в памяти только в то время, пока открыт текущий сеанс соединения с сервером. Как только соединение закрывается, все подобные модели удаляются.
Что входит в надстройку
На рисунке 24 показаны вкладки интеллектуального анализа данных, появляющиеся в Excel после установки надстройки и запуска программы и доступные после настройки службы Analysis Services.
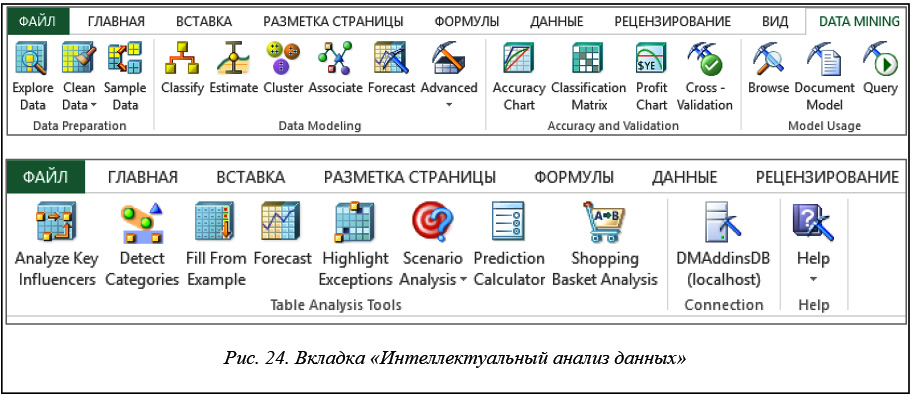
В набор SQL Server Analysis Services входят девять основных алгоритмов Data Mining.
Для решения задач классификации и прогнозирования в надстройку входит алгоритм построения деревьев решений (Microsoft Decision Trees).
Для выявления в исследуемом массиве данных связей, которые невозможно обнаружить простым просмотром этих данных, используется алгоритм кластеризации (Microsoft Clustering). В надстройке используются алгоритмы максимизации ожидания (Expectation Maximization) и K-ближайших соседей (K-Means).
Для решения задач классификации и прогнозирования Microsoft предлагает алгоритм «Наивный Байес» (Microsoft Naive Bayes).
Для осуществления прогнозирования по нескольким непрерывным переменным, а также для анализа корреляции между различными прогнозируемыми характеристиками по времени можно использовать алгоритм временных рядов (Microsoft Time Series). Алгоритм временных рядов является разновидностью алгоритмов построения деревьев авторегрессии ART (Auto Regressive Trees).
Если необходимо проанализировать последовательность каких-либо фактов, представляющих собой временные последовательности дискретных переменных, то можно использовать алгоритм кластеризации последовательности действий (Microsoft Sequence Clustering). Алгоритм является гибридом алгоритма последовательностей действий и алгоритма кластеризации и прогнозирует наступления последующих событий на основании уже осуществленного перехода между состояниями.
Для создания моделей классификации и регрессии путем конструирования многослойной нейронной сети перцептронов предназначен алгоритм построения нейронных сетей (Microsoft Neural Network).
В качестве частного случая алгоритма деревьев решений представлен алгоритм линейной регрессии (Microsoft Linear Regression), результат в котором получается при запрете на разбиение узлов в дереве решений.
В качестве частного случая алгоритма построения нейронных сетей Microsoft представлен алгоритм логистической регрессии (Microsoft Logistic Regression), получаемый при удалении скрытого слоя нейросети.
Для поиска частых закономерностей в исходном массиве данных предназначен алгоритм поиска взаимосвязей (Microsoft Association). В нашем случае будет применяться именно этот алгоритм, так как он является реализацией Apriori в SQL Server Analysis Services. Модели исходных данных по данному алгоритму создаются на основании исходных данных, и в них служба Analysis Services подсчитывает потенциальные наборы элементов (событий, продуктов, значений атрибутов и т.д., в зависимости от типа анализируемых данных).
Пример применения алгоритма поиска взаимосвязей на тестовой БД
БД службы SQL Server Analysis Services может быть представлена моделью на основе технологии OLAP, реляционной структуры или табличных данных. Приведем пример построения ассоциативных правил в Excel на тестовом примере, который организуем в виде наиболее простого и удобного для использования формата – таблицы MS Excel.
По требованиям алгоритма, входные табличные данные должны состоять из двух столбцов – столбца с уникальными идентификаторами элементов и столбца с атрибутами. Значения атрибутов должны быть текстовыми, и в БД не должно быть пустых строк. Исходную БД преобразуем к данному виду (рис. 25).
Для вызова «Мастера взаимосвязей» выберем кнопку на панели ИАД (рис. 26).
Далее необходимо задать исходные данные, параметры алгоритма и параметры структуры данных для построения модели службы Analysis Services.
На странице «Выбор исходных данных» задаем диапазон значений нашей таблицы (рис. 27).
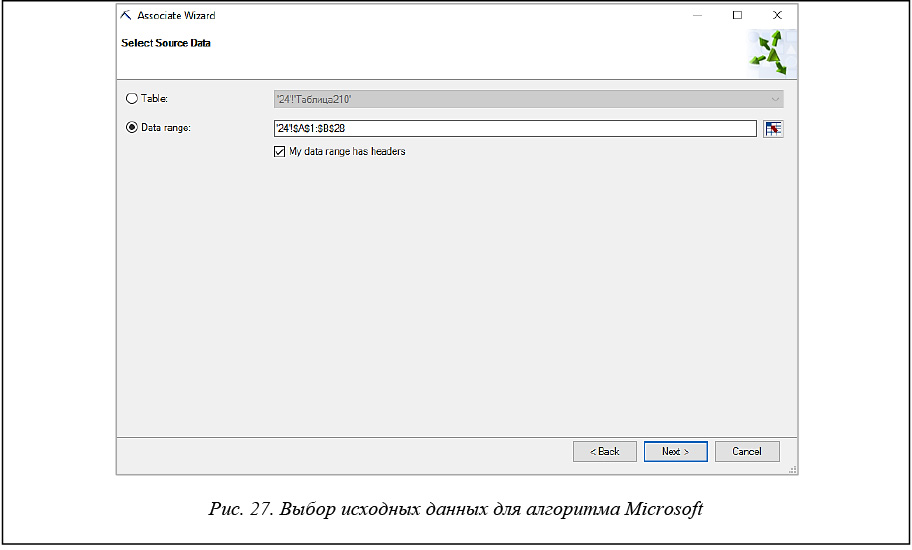
Далее необходимо выбирать столбец, определяющий транзакцию на странице «Поиск взаимосвязей» (рис. 28). В поле «Идентификатор транзакции» выбираем столбец-идентификатор (в данном случае TID), в поле «Элемент» – столбец с анализируемыми данными (List of items_IDs).
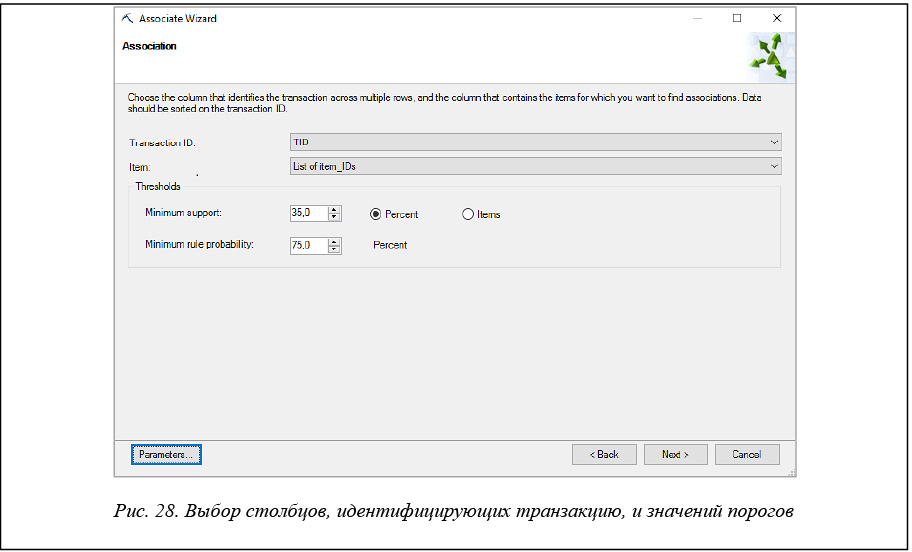
Также на этом этапе задаются пороги фильтрации результатов – минимальное несущее множество (поддержка) и минимальная вероятность правила.
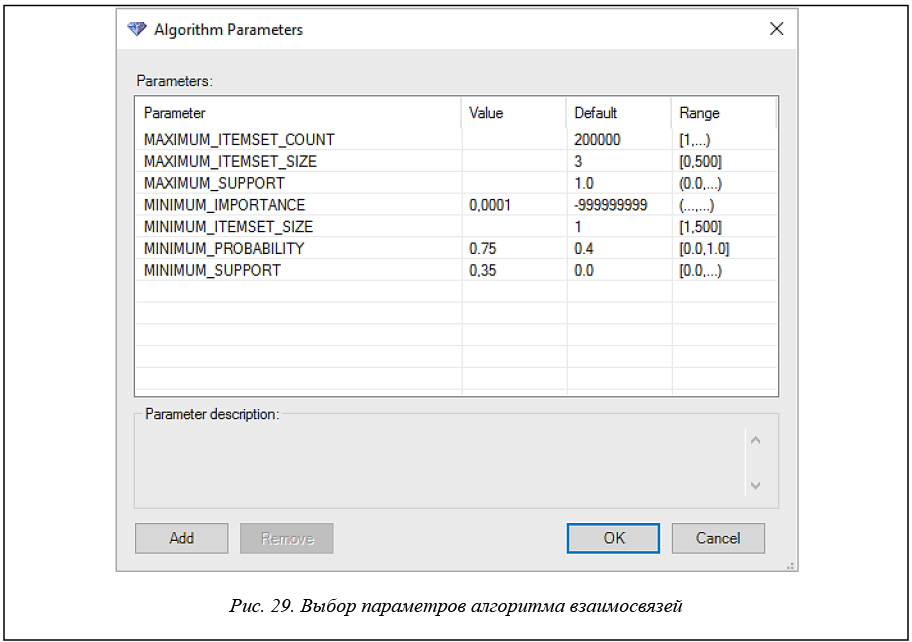
В помощнике «Параметры алгоритма» (рис. 29) задаются другие, необходимые параметры алгоритма. Значения порогов из предыдущей вкладки переписываются автоматически.
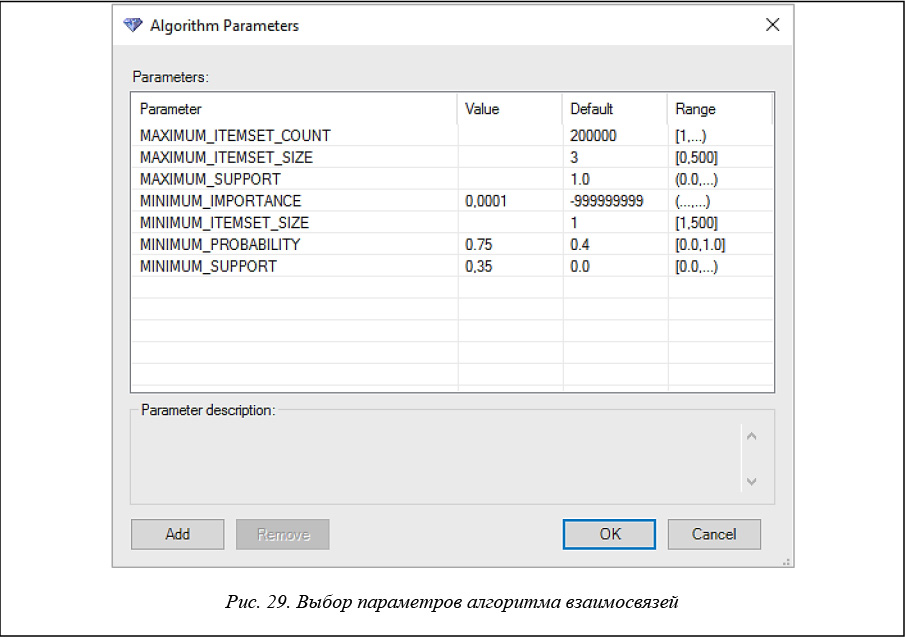
Опишем значения задаваемых параметров.
MAXIMUM_ITEMSET_COUNT задает максимальное число наборов элементов. При отсутствии данного параметра алгоритм формирует все возможные наборы.
MAXIMUM_ITEMSET_SIZE определяет максимальное число допустимых элементов в наборе. Если значение параметра равно 0, предельный размер набора элементов не задается.
MAXIMUM_SUPPORT задает верхнюю границу числа вариантов, поддерживаемых в наборе. Значение может быть задано как в процентах, так и числом.
MINIMUM_IMPORTANCE является пороговым значением важности для ассоциативных правил. Если важность правила меньше данного значения, то оно отфильтровывается.
MINIMUM_ITEMSET_SIZE определяет минимальное число элементов в наборе.
MINIMUM_PROBABILITY – минимальная вероятность точности правила. Правила с вероятностью, меньше заданной, не создаются.
MINIMUM_SUPPORT – минимальная поддержка правила.
Самыми значимыми для алгоритма являются параметры вероятность (MINIMUM_PROBABILITY) и поддержка (MINIMUM_SUPPORT). С их помощью можно регулировать количество и качество правил, которые будут получены в результате работы алгоритма взаимосвязей Microsoft.
Для каждого создаваемого правила службы Analysis Services вычисляют такой параметр, как важность. Задание параметра (MINIMUM_IMPORTANCE) позволяет фильтровать правила по этому параметру, рассматривая только правила с важностью, большей минимальной. Ранее мы уже говорили, что по документации авторам не удалось восстановить алгоритм расчета значения параметра importance. Судя по анализу результатов экспериментов, этот параметр является аналогом параметра lift, сохраняя порядок на правилах, задаваемый параметром lift [8].
На странице «Готово» (рис. 30) можно ввести уникальное имя для структуры данных и модели, под которыми данный экземпляр модели будет храниться на сервере. На этой странице можно выбрать также следующие параметры модели:
– параметр «Использовать временную модель» отвечает за сохранение модели на сервере; если не отметить данный параметр, модель удалится при закрытии окна надстройки Excel;
– параметр «Разрешить детализацию» позволяет получить доступ к данным модели; при включенном параметре будет доступна возможность просмотра исходных данных при щелчке на том или ином наборе элементов;
– параметр «Обзор моделей» отвечает за открытие окна, где выводятся правила, наборы элементов и диаграмма сети зависимостей элементов наборов.
После нажатия кнопки «Готово» клиент начнет обрабатывать входные данные и строить обучающую модель для алгоритма. Во время работы надстройки будет показано окно, отображенное на рисунке 31.
Так как включен параметр «Обзор модели», после выполнения алгоритма всплывает окно «Обзор», включающее следующие вкладки:
– правила (рис. 32);
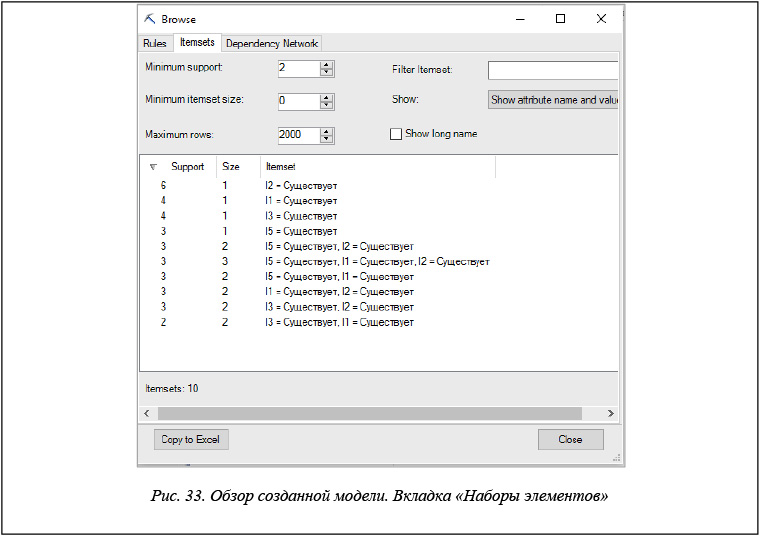
– наборы элементов (рис. 33);
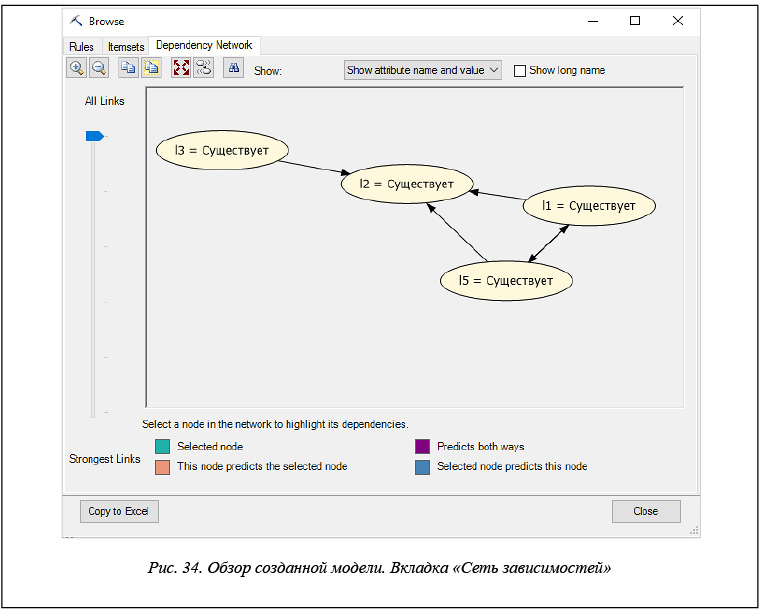
– сеть зависимостей (рис. 34).
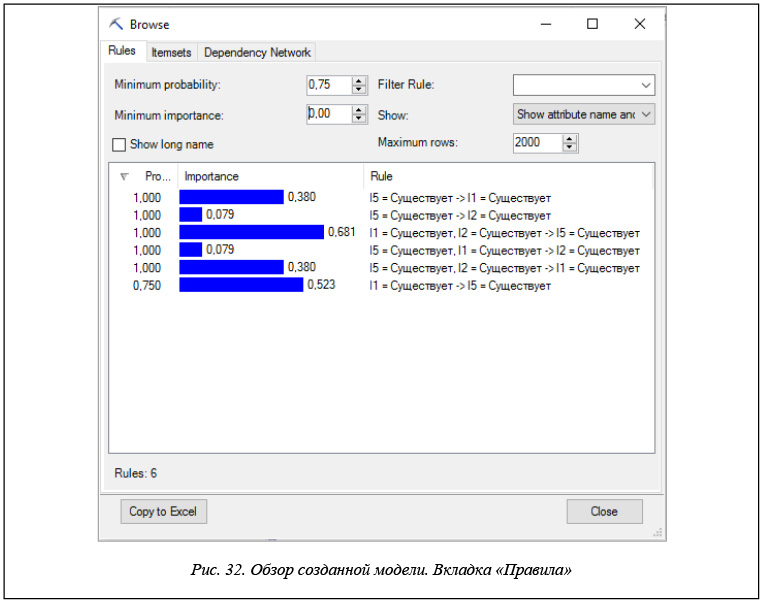
Во вкладке «Правила» представлена информация о
созданных алгоритмом правилах и их относительных значениях. Для каждого набора правил средство просмотра дает возможность посмотреть значения вероятности и важности.
Вероятность показывает, с какой достоверностью выполняется то или иное правило. В данной вкладке можно изменить значение минимальной вероятности для того, чтобы выбрать более достоверные правила. Изначальное значение «Минимальной вероятности» – это пороговое значение, которое задается при создании модели. Понизить его нельзя, но повысить можно.
Важность – необходимая характеристика для измерения степени информативной ценности правила. Есть возможность задать фильтр посылки правила с помощью параметра «Правило фильтра». Параметр «Максимальное число строк» позволяет ограничить количество правил на экране.
Изменение параметров в данной вкладке влияет только на отображение и не влияет на созданную модель. Если нужно снизить значение вероятности, придется строить еще одну модель и задавать соответствующий параметр в окне «Параметры алгоритма».
На вкладке «Наборы элементов» можно просмотреть список наборов, составляющих правила. Для каждого набора указываются его поддержка, размер и вероятность.
Размер набора отражает количество элементов в наборе. Если видеть одиночные наборы в списке не требуется, можно задать значение соответствующего параметра в окне «Наборы элементов».
Количество строк наборов элементов в данной вкладке можно также ограничить параметром «Максимальное число строк».
Изменение параметров в данной вкладке, как и в предыдущей, влияет только на отображение модели. При необходимости изменить значение поддержки нужно построить другую модель.
Во вкладке «Сеть зависимостей» надстройка Excel дает граф зависимостей между элементами наборов. Каждый узел графа представляет пару «атрибут–значение. Каждое ребро показывает направление корреляции.
В графе зависимостей можно найти нужный элемент и отобразить наиболее прочные связи.
Данные всех вкладок окна «Обзор» можно поместить на отдельный лист документа Excel кнопкой «Копировать в Excel».
Сравнение трех инструментов. Анализ результатов. Эффективность
Сравнение трех инструментов построения ассоциативных правил начнем с выяснения вопроса о том, дают ли все инструменты одинаковые результаты на одной и той же БД, что заодно позволяет убедиться в корректности их работы. Выяснять этот факт удобнее всего на тестовом примере, для которого нетрудно самому построить правила и провести их фильтрацию в соответствии с определениями параметров, характеризующих правила.
Приведем ранее показанный файл с правилами, построенными для тестового примера системой Ментор (рис. 35).
Правила построены при поддержке support, большей 0,35, и достоверности confidence, большей 0,75. Таких правил шесть, и для тестового примера нетрудно проверить, что построены все правила и лишних правил нет. Правила отфильтрованы по двум критериям – support и confidence. Если отфильтровать правила и по параметру lift, например, рассматривать правила, для которых lift >= 2, то останутся для рассмотрения только два правила:
I1, I2 => I5 и обратное правило I5 => I1, I2.
Какие же результаты показывают другие инструменты на тестовом примере? Инструментарий R строит пять правил из шести. Все характеристики построенных правил совпадают с характеристиками правил, построенными системой Ментор. Единственное, но важное отличие в том, что пропущено правило I5 => I1, I2. Причина в том, что система R заточена на построение ассоциативных правил для решения задачи классификации. В задачах классификации заключение правила содержит только один элемент, задающий класс объекта. Поэтому правила, содержащие в заключении несколько элементов, просто не строятся. Это, конечно, упрощает систему построения правил, но, на взгляд авторов, является
серьезным ограничением для широкого круга задач, отличных от задачи классификации.
В системе Ментор возможность учета специфики задачи классификации решается по-другому. Здесь строятся все правила с заданной частотой и достоверностью, а потом можно задать дополнительный фильтр на посылку и заключение правила. Так что легко получить все правила, характеризующие данный класс объектов.
Что же показывает инструментарий Microsoft на тестовом примере? Если задать те же характеристики поддержки и достоверности (в терминах Microsoft – support и probability), то будет построено одиннадцать правил (рис. 36).
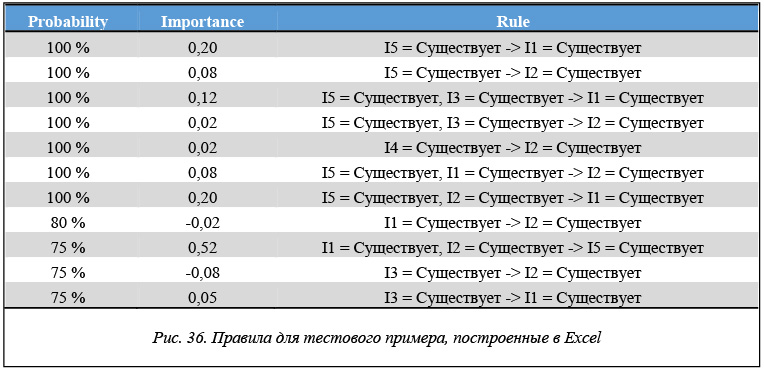
Пять из одиннадцати построенных правил совпадают с правилами, построенными инструментарием R и системой Ментор. Шесть правил – это дополнительные правила, которые не были построены ни в R, ни в системе Ментор. Чем это объясняется? Дело в том, что построенные одиннадцать правил отфильтрованы по двум параметрам – probability и importance, но не отфильтрованы по параметру поддержки support, хотя граничное значение для него задавалось. Удивительно, но среди правил присутствует правило, содержащее параметр I4, который не является частым набором и потому в соответствии с концепцией алгоритма Apriori ни одно правило, содержащее этот параметр, не должно появляться.
Отметим еще одну особенность инструментария Analysis Services при построении правил на тестовом примере. При многократном запуске тестового примера результаты носят отчасти случайный характер. Пять правил, которые строятся системами Ментор и R, строятся всегда, а дополнительные правила могут меняться. На рисунках 37 и 38 показаны результаты двух сеансов работы в Excel для тестового примера с одним и тем же набором параметров.
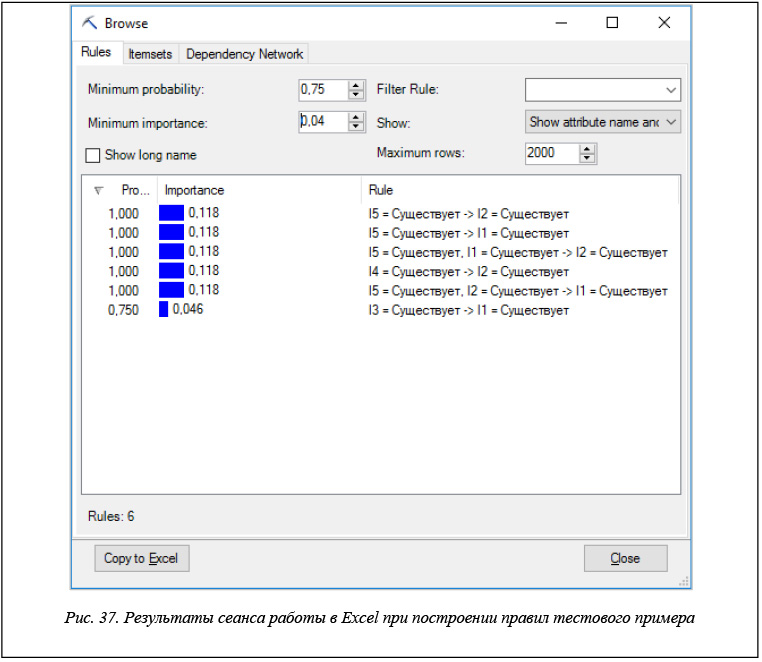
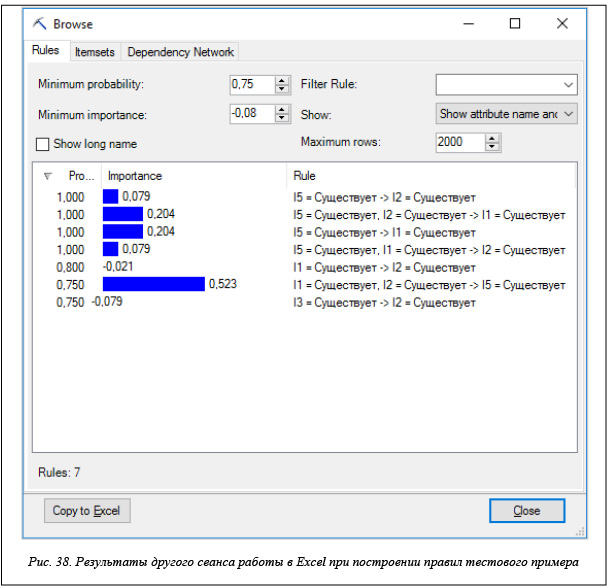
Случайность получаемых результатов объясняется тем, что каждый сеанс отличается значением минимальной важности, которое случайно от сеанса к сеансу и не зависит от того, какое значение устанавливается в настройках для этого параметра.
Нетрудно заметить, что от сеанса к сеансу меняется не только число дополнительных правил, но и характеристики правил – вероятность и важность.
Эти результаты свидетельствуют, что данный сервис в инструментарии Microsoft недоработан и пользоваться им следует с осторожностью. Он действительно позволяет построить нужные правила, но может построить и дополнительные правила, не удовлетворяющие требованиям частоты и достоверности. После построения правил, повышая их важность, можно отфильтровать лишние правила, но гарантировать это нельзя.
Наши эксперименты показывают, что эффект случайности на больших БД сказывается в меньшей степени.
Ранее мы говорили, что параметр probability является аналогом параметра confidence, однако количественные значения этих параметров не совпадают. Так, для построенного правила I1 => I2 указанное значение probability = 0,8, в то время как confidence для него равен 5/7, что меньше 0,72, и потому это правило отфильтровывается в R и Ментор.
Подводя итог, можно заметить, что правила, строящиеся инструментарием Microsoft Analysis Services, позволяют получить набор правил, строящихся в R. Однако этот набор дополняется правилами, которые в R будут отфильтрованы по параметрам support и confidence.
Фильтрация правил по параметру importance позволяет прийти к согласованным с R правилам, однако гарантировать полное совпадение нельзя.
Важно также отметить, что так же, как и в R, инструменты Analysis Services не строят правил, заключение в которых содержит несколько параметров. Из трех рассматриваемых инструментов такие правила строятся только в системе Ментор.
Эффективность
Одной из важнейших характеристик инструментария является время построения правил для больших БД.
В таблице 1 и на рисунках 39 и 40 приведены данные времени расчета правил для каждого инструмента в зависимости от размера БД. Эти данные получены для модельной БД, каждая транзакция которой представляет набор из 60 возможных свойств. Правила строятся при минимальной поддержке и достоверности support = 0,05, confidence = 0,1.
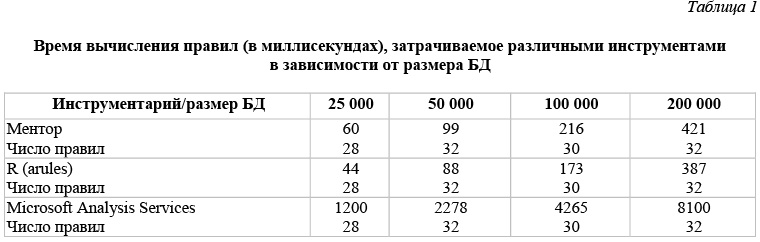
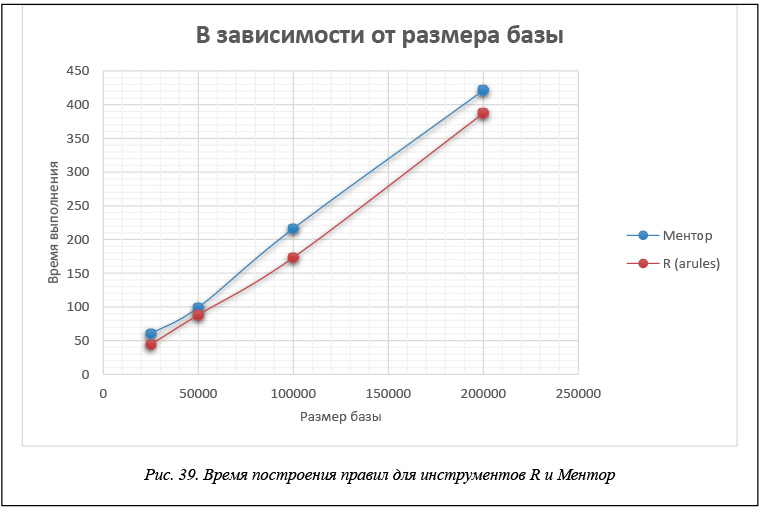
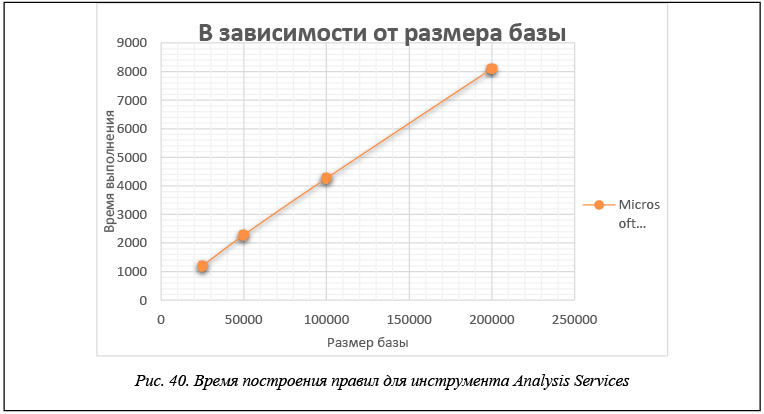
В таблице 2 и на рисунках 41 и 42 приведены данные времени расчета правил для каждого инструмента в зависимости от значения минимальной поддержки support. Эти данные получены для модельной БД, каждая транзакция которой представляет набор из 60 возможных свойств, когда размер базы составляет 200 000 транзакций. Правила строятся при минимальной достоверности confidence = 0,1.
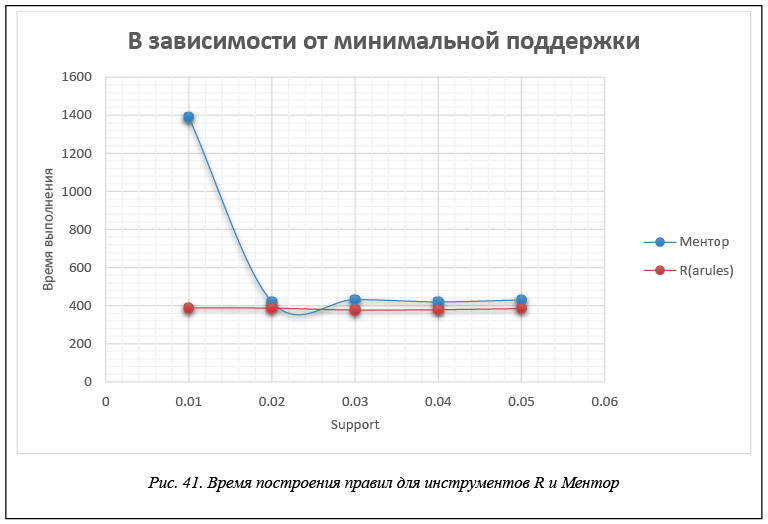
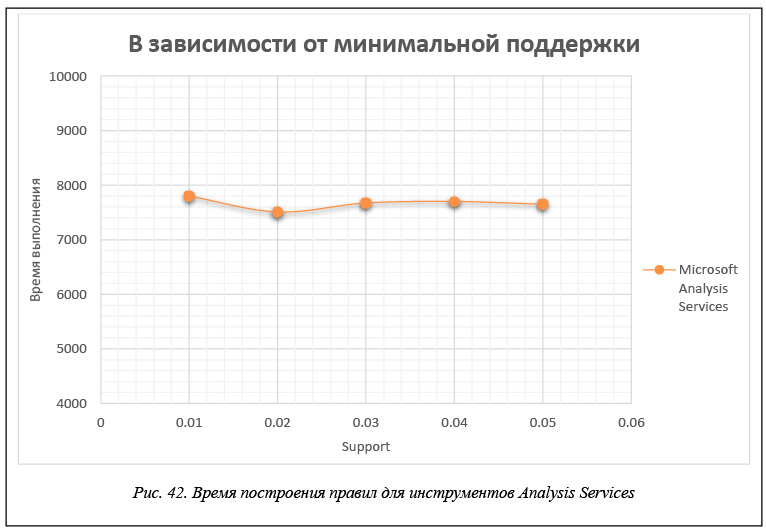
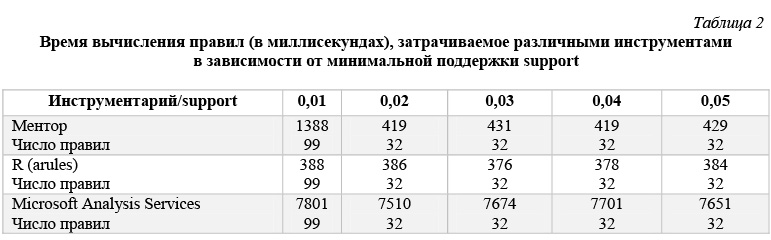
В таблице 3 и на рисунках 43 и 44 приведены данные времени расчета правил для каждого инструмента в зависимости от значения минимальной достоверности confidence. Эти данные получены для модельной БД, каждая транзакция которой представляет набор из 60 возможных свойств, когда размер базы составляет 200 000 транзакций. Правила строятся при минимальной поддержке support = 0,01.
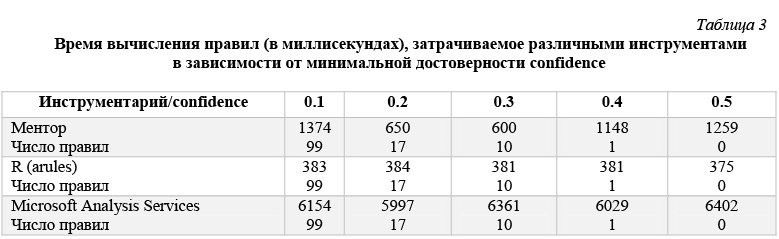
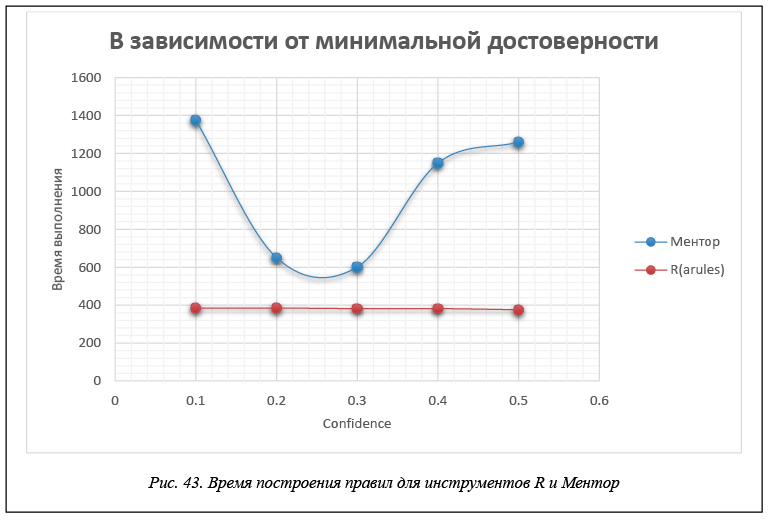
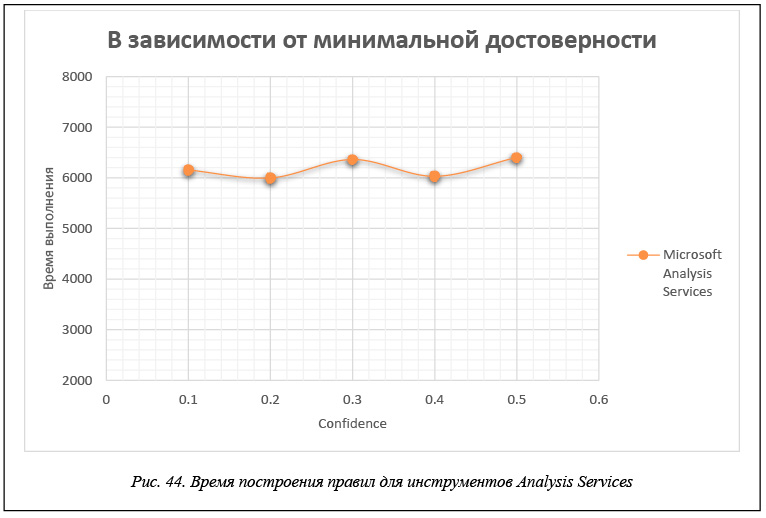
Тестовые базы, по данным которых построены таблицы 1–3, моделируют ситуацию, достаточно часто возникающую при анализе потребительских корзин, когда строятся правила типа «один–один» с единичной посылкой и единичным заключением. Как показывают приведенные результаты, все рассматриваемые инструменты строят одинаковое число правил для этой БД и все построенные правила совпадают. Что касается времени вычислений, то измерить точное время, требуемое для построения правил, возможно только для инструментов R и Ментор. Для инструмента Microsoft Analysis Sevices, где происходит передача данных от клиентского приложения, роль которого играет Excel, к серверу – Microsoft SQL Server, измерить время построения правил не удается, и поэтому приводимое время следует считать условным.
Правила вида «один–один» представляют определенный интерес. Однако наибольший интерес представляют такие БД, в которых найденные правила в посылке и заключении содержат несколько элементов. Примером может служить задача классификации, когда совокупность признаков позволяет отнести объект к тому или иному классу. Не менее интересна ситуация, когда удается установить, что одна совокупность признаков указывает на высокую вероятность появления другой совокупности.
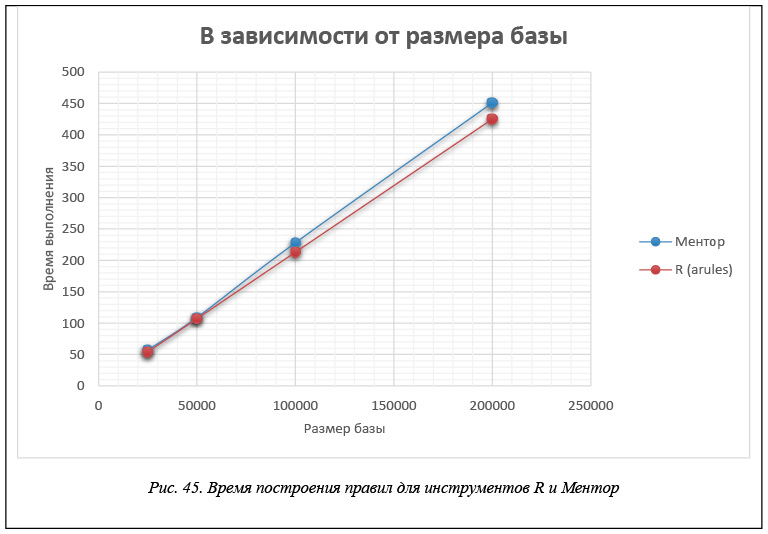
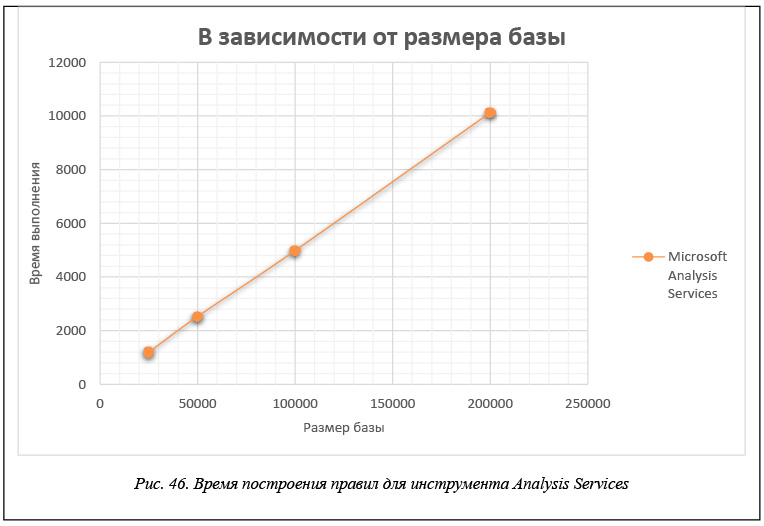
Мы построили тестовые БД для таких ситуаций. Приведем таблицы 4–6, аналогичные таблицам 1–3, и соответствующие им графики на рисунках 45–50 для тестовых БД, извлекаемые правила которых содержат несколько элементов в посылке и в заключении.
Правила строятся при минимальной поддержке support = 0,25 и достоверности confidence = 0,4.
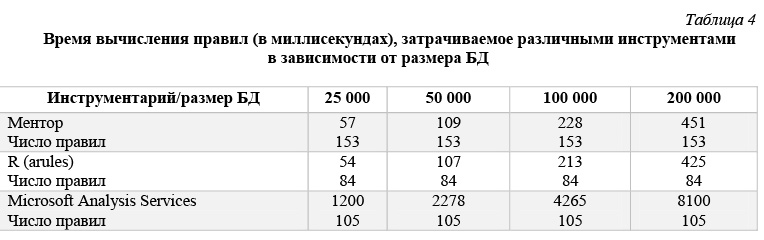
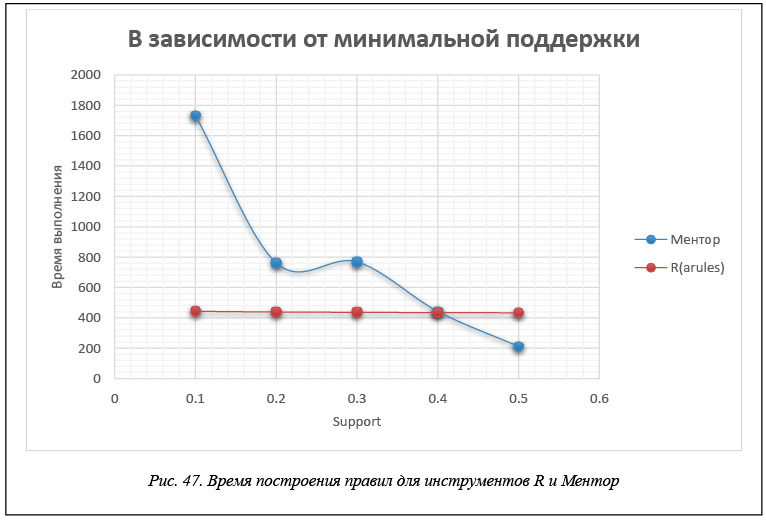
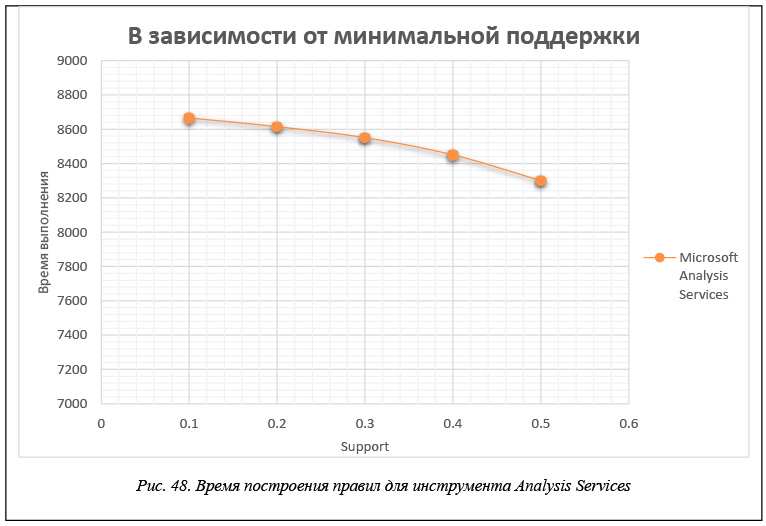
В таблице 5 и на рисунках 47 и 48 приведены данные времени расчета правил для каждого инструмента в зависимости от значения минимальной поддержки support. Эти данные получены для модельной БД, каждая транзакция которой представляет набор из 60 возможных свойств, когда размер базы составляет 200 000 транзакций. Правила строятся при минимальной достоверности confidence = 0,75.
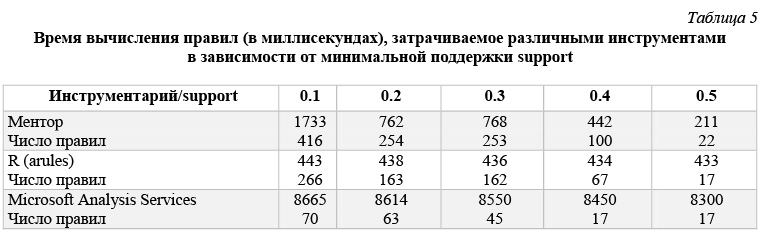
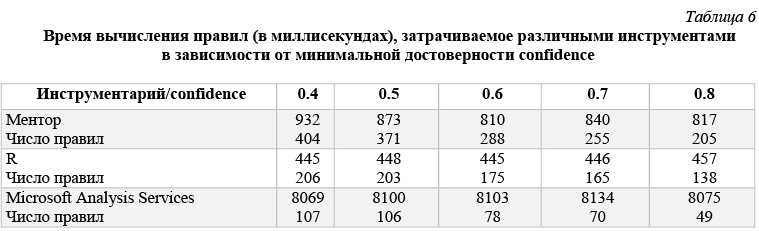
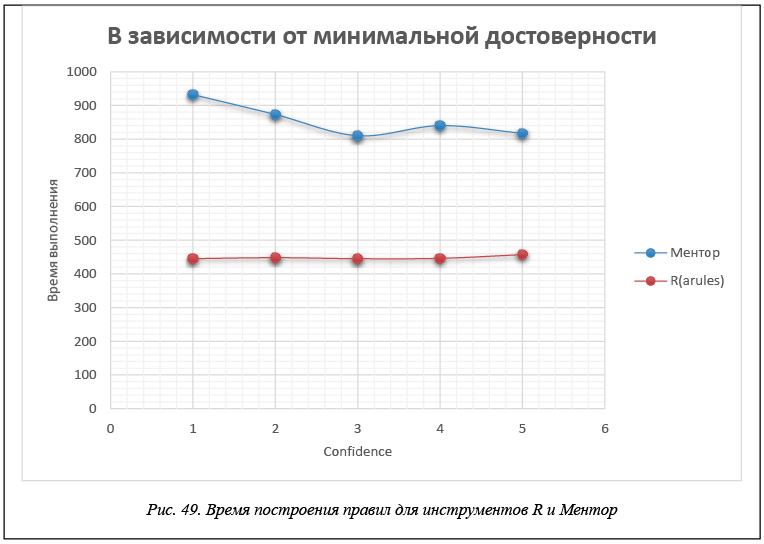
В таблице 6 и на рисунках 49 и 50 приведены данные времени расчета правил для каждого инструмента в зависимости от значения минимальной достоверности confidence. Эти данные получены для модельной БД, каждая транзакция которой представляет набор из 60 возможных свойств, когда размер базы составляет 200 000 транзакций. Правила строятся при минимальной поддержке support = 0,2.
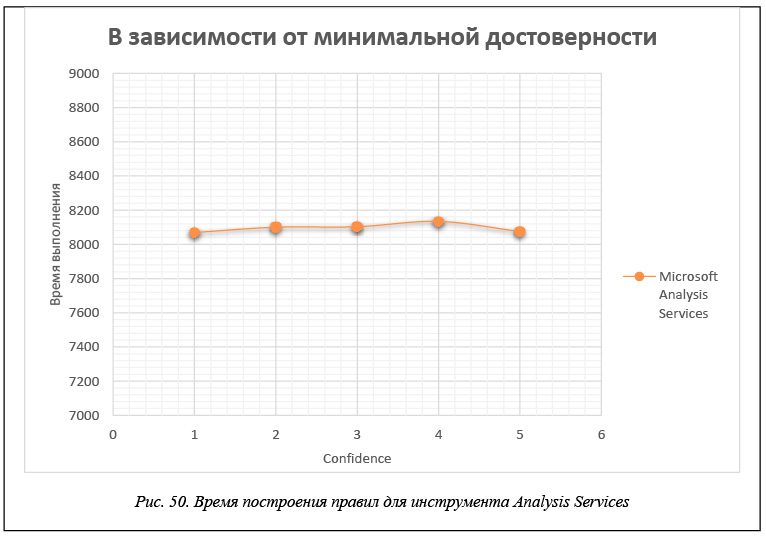
Анализ результатов, приведенных в таблицах 4–6, показывает, что рассматриваемые инструменты строят различное число достоверных правил. Причина в том, что, как отмечалось, правила, извлекаемые из тестовых БД, носят более сложный характер, поскольку содержат несколько элементов как в посылке, так и в заключении. По этой причине число правил, построенных в системе Ментор, больше числа правил в R (arules) и Analysis Services, так как эти инструменты не строят правила, имеющие в заключении несколько элементов. Расхождение в числе правил между R и Analysis Services, показанные, например, в таблице 6, объясняется разными критериями фильтрации правил, используемыми в этих системах. Тем не менее, удается настроить фильтры так, что оба инструмента строят одну и ту же систему правил.
Для проведения полного анализа строящихся правил разными инструментами рассмотрим тестовый вариант, приведенный в последнем столбце таблицы 5, когда рассматривается БД из 200 000 записей при минимальной поддержке support = 0,5 и минимальной достоверности confidence = 0,75. На рисунке 51 приводится система из 22 правил, строящихся в системе Ментор для этого случая.
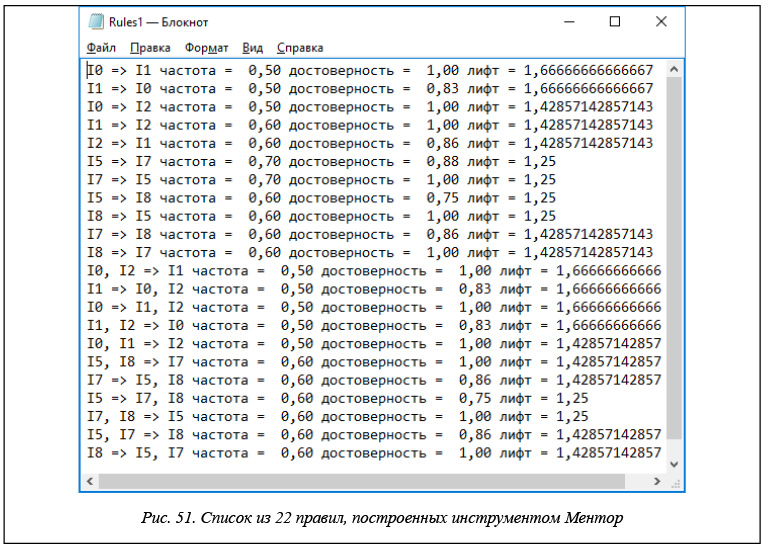
Для этого же тестового случая файл с правилами, построенными в инструментарии R, имеет вид, представленный в таблице 7.
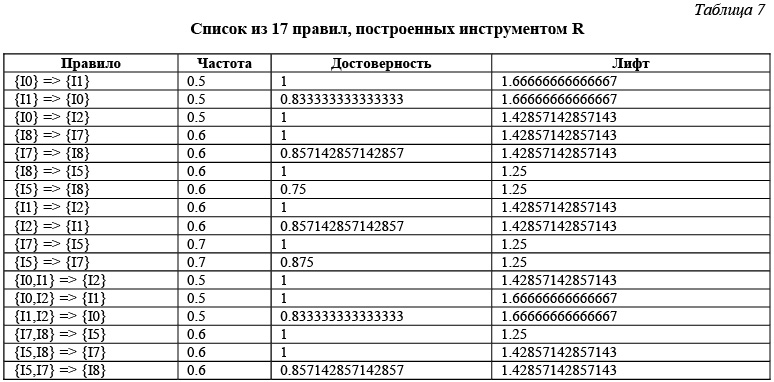
Сравнивая правила, построенные в R и в Ментор, мы видим, что все 17 правил, построенные в R, строятся и в системе Ментор. Все характеристики построенных правил – частота, достоверность, лифт для этих правил – полностью совпадают. Система Ментор строит еще 5 правил, удовлетворяющих требованиям по частоте и достоверности, правила, в которых заключение содержит несколько элементов. На взгляд авторов, такие правила представляют несомненный интерес. То, что они не строятся инструментами R и Analysis Services, является недостатком, присущим этим инструментам.
В инструментарии Microsoft соответствующий файл правил для рассматриваемого тестового случая имеет вид, приведенный на рисунке 52.
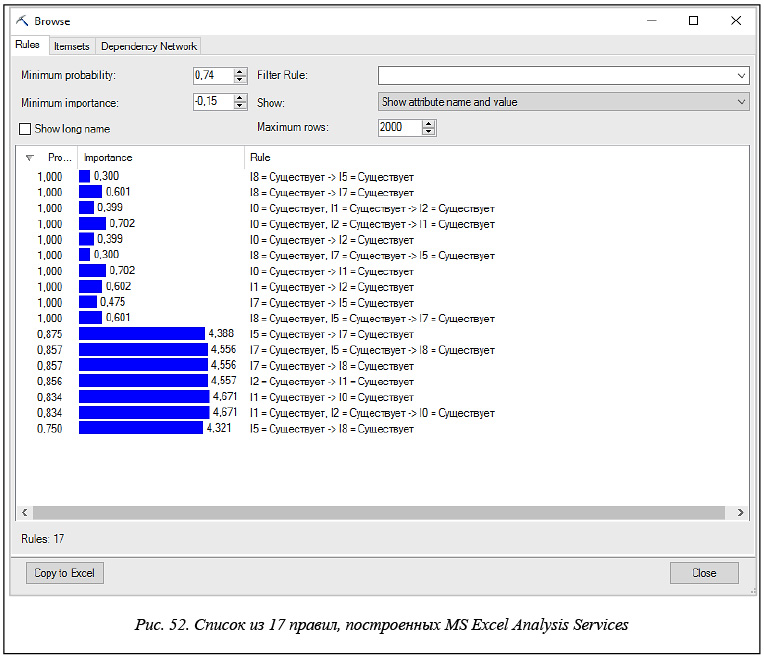
Этот инструмент строит те же 17 правил, что и система R (arules). Значения параметра probability (вероятность) полностью совпадают со значениями параметра «достоверность» в R. Корреляция между значениями параметров importance (важность) и lift (лифт) не обнаруживается.
Достоинства и недостатки инструментариев
Подводя итоги, отметим главные достоинства и недостатки рассмотренных инструментов Data Mining, применимых для извлечения ассоциативных правил из БД. Прежде всего отметим, что все рассмотренные инструменты с успехом могут применяться для решения поставленной задачи. Однако у каждого из них есть свои достоинства и недостатки.
Инструмент Microsoft Analysis Services
Главное достоинство этого инструмента в том, что наряду с возможностью построения ассоциативных правил этот инструментарий предоставляет возможность использования других многочисленных алгоритмов интеллектуального анализа данных.
Что же касается конкретного сервиса для построения ассоциативных правил, то этим инструментом следует пользоваться, на взгляд авторов, с большой осторожностью. Он позволяет строить правильное множество достоверных правил, как в случае, показанном на рисунке 52. Вместе с тем на простых тестах он давал неоднозначные результаты (см. рис. 37, 38).
Авторам так и не удалось выяснить точный смысл и алгоритм расчета параметра importance (важность), используемого в этом сервисе.
Существенным недостатком является и то, что не строятся правила, имеющие в заключении несколько элементов.
Закрытость кода не позволяет вносить какие-либо изменения, учитывающие специфику решаемой задачи.
Инструментарий R (arules)
Этот инструмент является лидером по эффективности построения правил. Как и остальные инструменты, зависимость времени построения правил от размера БД является линейной, что говорит о высоком качестве используемого алгоритма. Более того, время построения правил практически не зависит от числа строящихся правил, варьируемого в зависимости от выбранных параметров, – минимальной частоты и минимальной достоверности правил.
Существенным недостатком является то, что не строятся правила, имеющие в заключении несколько элементов.
Код реализуемого в пакете arules алгоритма доступен на сайте Борглета [3], но вряд ли может быть модифицирован кем-либо, помимо автора, ввиду его сложности и отсутствия описания реализованного алгоритма. Судя по данным, приводимым на сайте, код совершенствовался в течение многих лет. Приводимый псевдокод явно не соответствует реализации алгоритма.
Использование этого инструмента требует знакомства с языком R и соответствующей средой разработки. Тем не менее, скрипт для запуска пакета arules достаточно прост и интуитивно понятен.
Инструментарий Ментор
Трудно оценить собственную разработку. Всегда кажется, что она имеет несомненные достоинства. Тем не менее, авторы постарались дать объективную оценку этого инструмента. Одним из важных его достоинств в сравнении с рассматриваемыми инструментами является построение полной системы правил, удовлетворяющих принятым ограничениям по частоте и достоверности.
По времени построения правил наша реализация уступает инструменту arules. Но проигрыш относительно невелик. Для достаточно больших БД из 200 000 записей время построения правил обычно менее одной секунды.
Из-за способа представления данных БД имеет меньший объем, чем другие распространенные форматы.
Серьезным ограничением является ограничение на число факторов, входящих в транзакции БД.
В данной реализации их не должно быть более 63. Однако это ограничение легко преодолевается переходом от стандартного класса enum, задающего класс, описывающий перечисление в библиотеке классов FCL, к собственному классу long_enum.
Открытость кода и простота алгоритма позволяют модифицировать систему Ментор в случае необходимости учета каких-либо специфических особенностей задачи.
В системе отсутствуют графические средства отображения построенных правил, имеющиеся в инструментах R и Analysis Services. На взгляд авторов, эти средства не играют важной роли в понимании сути правил. В любом случае система является открытой и может быть дополнена, коль скоро такие средства будут признаны полезными.
Литература
- Piatetsky-Shapiro G. Data mining and knowledge discovery – 1996 to 2005: overcoming the hype and moving from “university” to “business” and “analytics”. Data Mining and Knowledge Discovery Journ., 2007, рр. 99–105.
- Agrawal R. and Srikant R. Fast algorithms for mining association rules in large databases. Proc. 20th Intern. Conf. VLDB, 1994, рр. 487– 499.
- Christian Borglet’s web pages. URL: http://www.borgelt.net/apriori.html (дата обращения: 17.03.2016).
- Биллиг В.А., Иванова О.В., Царегородцев Н.А. Построение ассоциативных правил в задаче медицинской диагностики // Программные продукты и системы. 2016. № 2.
- Ihaka R., Gentleman R. R: A language for data analysis and graphics. Journ. of Computational and Graphical Statistics, 1996, vol. 5, no. 3, pp. 299–314.
- The comprehensive R archive network. URL: http://cran.r-project.org (дата обращения: 17.03.2016).
- Биллиг В.А. Основы объектного программирования на C#. М.: ИНТУИТ, Бином, Лаборатория знаний, 2010. 582 с.
- MacLennan J., Tang Z., Crivat B. Data mining with Microsoft SQL Server 2008. Wiley Publ., 2009, 676 p.
- Описание алгоритма взаимосвязей Microsoft. URL: https://msdn.microsoft.com/ru-ru/library/ms174916(v=sql.105).aspx (дата обращения: 17.03.2016).
- Обзор логической архитектуры службы SSAS URL: https://technet.microsoft.com/ru-ru/library/feedback/additional/ms174587.aspx (дата обращения: 17.03.2016).
- НОУ ИНТУИТ. URL: http://www.intuit.ru/studies/courses/568/424/lecture/9645 (дата обращения: 17.03.2016).
ASSOCIATION RULES. COMPARED ANALYSIS OF THE TOOLS
Billig V.A., Ph.D., Vladimir-Billig@yandex.ru;
Korneeva E.I., Master Student, Yelena.Korneeva@yandex.ru;
Syabro N.A., Master Student, 6xitix6@gmail.com
(Tver State Technical University, Nikitin Quay 22, Tver, 170026, Russian Federation)
Annotation. An algorithm of the building association rules is one of the most important algorithms of intellectual analysis of a database. In this article are discussed advantages and disadvantages of three tools designed for discovery of the association rules in the database. One of these tools is the service included in Microsoft SQL Server. Special Add-In included in Microsoft Excel plays the role of a client of the server. Another tool is a special package “arules” included in R Studio – environment for programming on R language. The third tool called system "Mentor" is created by authors of this article. The article describes the conditions of application tools and analyses their effectiveness on examples of the testing data bases.
Keywords: association rules, intellectual data analysis, data mining, knowledge data discovery, algorithm Apriori, data bases, Microsoft services, Microsoft analysis service, programming language R, package arules, system Mentor, AddIn Excel, Microsoft SQL server, enumeration, scale.
Комментарии