(Работа выполнена при частичной финансовой поддержке РФФИ (гранты №№ 15-07-00341,
16-07-00350), Программы «Дальний Восток» (проект 15-I-4-011 о) и Программы
Президиума РАН № I.33П «Фундаментальные проблемы математического моделирования»)

Большая часть методов построения трехмерных моделей реальных объектов использует дальностные данные, получаемые с помощью стереокамер, лазерных дальномеров или алгоритмов компьютерного зрения по серии изображений этого объекта, снятого с разных точек. В научной литературе на такие данные ссылаются как на дальностные изображения (range images) или карты глубин (depth maps) [1].
С каждым пикселем range image/depth map связывается расстояние до видимой точки объекта в пространстве сцены. Эти пространственные данные могут быть представлены в виде облака точек в трехмерном пространстве или в виде триангуляционной поверхности. Наряду с задачей объединения этих триангуляционных сеток, подразумевающей построение единой связной оболочки без дублирования участков поверхности, стоит задача зашивки дыр и построения текстуры. Зашивка дыр происходит на этапе заполнения неявной функции в воксельном пространстве, хотя методы зашивки могут использоваться на этапе обработки триангуляционной модели, как, например, в [2, 3]. Под дырами подразумеваются участки, где должна быть поверхность, но по каким-либо причинам она не была построена ни на одном из видов. Основная причина появления дыр – перекрытие одних участков поверхности другими.

Предлагаемый в настоящей статье метод построения единой целостной трехмерной модели основывается на подходе, предложенном в [4, 5], а также на более ранних работах ([6, 7]) и направлен на
преодоление указанных недостатков. Работа выполнялась в контексте решения авторами более общей задачи по созданию трехмерных сцен на последовательностях изображений. Важными требованиями к алгоритмическому решению задачи являются высокая скорость обработки данных и экономное использование оперативной памяти, поскольку для насыщенных сцен со сложными объектами может потребоваться много видов с большим количеством описывающих треугольников (порядка 106–107). Вклад авторов состоит в разработке оригинального алгоритма, в котором осуществляется построение гибридной
весовой функции для слияния текстур с учетом таких факторов, как угол наблюдения, тень/пересвет и близость к краю скана; обеспечивается оптимизация вычислений за счет эффективной структурной организации данных; достигается высокая скорость обработки данных за счет реализации параллельных вычислений на многоядерных процессорах.

Обзор существующих методов

Как показывает анализ известных работ, для решения задачи объединения триангуляционных сеток
и зашивки дыр на этих сетках в основном применяются два подхода. При первом подходе объединение и зашивка ведутся непосредственно на самой триангуляционной сетке [8]. Его основной недостаток – генерация взаимопересекающихся поверхностей при работе над сетками, имеющими сложную, составную топологию.

Более перспективным представляется воксельный подход, основанный на использовании воксельной структуры пространства сцены. Основным преимуществом предложенного решения является сведение исходной задачи к известной задаче построения изоповерхности в скалярном поле [4]. Этим же коллективом разработчиков был предложен и метод зашивки дыр [5], использующий диффузное размытие построенной весовой функции внутри воксельной структуры. Недостатками данного метода можно считать высокую ресурсоемкость, а также артефакты на результирующей модели [5].В работах других авторов предлагается использовать октодерево [9], чтобы сократить время работы, а также альтернативный метод расчета весовой функции [10], направленный на зашивку дыр. Однако проблема артефактов
по-прежнему остается, а время обработки даже небольших объемов (285x360x400) составляет несколько часов.

Существует довольно много подходов, применяемых для текстурирования реконструированных объектов, однако для каждого метода реконструкции с его ограничениями необходимо подбирать свой метод текстурирования. В текущем методе подразумевается, что сканер стоит неподвижно, а модель вращается на специальной площадке, поэтому для каждого участка поверхности меняется освещение, а, например, в [11] модель стоит неподвижно, а сканер перемещается вокруг, поэтому модель освещена одинаково для разных видов и перед авторами стоит задача убрать погрешности сканирования. В работе [12] авторы имеют дело с низкополигональными объектами и, помимо прочего, решают задачу частичного перекрытия треугольников. В нашем случае речь идет о модели с треугольниками, текстура которых имеет площадь, близкую к площади одного–двух пикселей, и решать задачу частичного перекрытия не имеет смысла. Но в целом эти методы близки к предложенному в данной статье.

В [11] используется блендинг с равновесным участием всех видов. Это хорошо работает, если освещение модели менялось незначительно и не появились дополнительные тени. Предложенный в данной статье метод дает лучший результат, чем равновесный блендинг. В [12] используется блендинг с учетом веса по наклону нормали от вектора наблюдения и веса по глубине, но не учитывается вес по дистанции от края скана, а именно на краю скана обычно образуются треугольники с максимальными искажениями, и они могут дать некорректные результаты. Также не учитывается вклад теней и пересветов.

Стоит отметить и скорость работы. Для [11] – это 10–30 минут для 10–20 тысяч треугольников, для [12] – это 1–4 минуты для 10–15 тысяч треугольников. Предложенным методом за 0,5–1,5 минуты обрабатывается 2–5 млн треугольников, что на несколько порядков быстрее. Однако стоит отметить, что из-за метода съемки нет необходимости решать задачу устранения неточности при сканировании.

Воксельный метод объединения

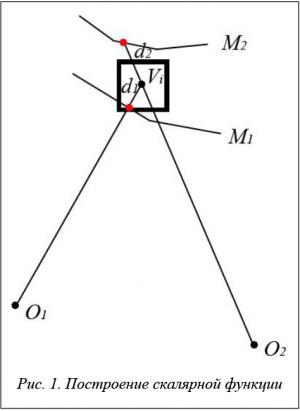
Задача формулируется следующим образом. Имеются n видов, для каждого из которых на предварительном этапе была построена поверхность в виде пространственной триангуляционной сетки. Триангуляционная сетка строилась по 2D-триангуляции на регулярной пиксельной решетке изображения с использованием карты глубин. Заметим, что карта глубин вычисляется для точек, видимых на данном изображении. Метод работает в воксельном пространстве сцены. Используется непрерывная неявная функция D(Vi), представленная значениями в узлах воксельной решетки. Функция конструируется как взвешенная сумма получаемых для n видов расстояний d1(Vi), d2(Vi), …, dn(Vi) от точки Vi до ближайшей поверхности (рис. 1). Расстояние dj берется на луче, направленном из центра проекций вида j в точку Vi, и является величиной со знаком (положительное для точек, находящихся перед поверхностью, и отрицательное для точек за поверхностью).

В качестве весовой функции W(Vi) берется скалярное произведение вектора нормали к поверхности и вектора направления на точку наблюдения. Такой выбор исходит из предположения, что при корреляционном подходе к определению расстояния до поверхности степень неопределенности для наклонных поверхностей выше, чем для поверхностей, наблюдаемых под прямым углом.

Для вычисления D и W используются следующие инкрементальные правила:

где i – номер вокселя;  j – номер вида.

Весовая функция W(Vi) – константа для всех вокселов до видимой поверхности (для данного вида),
а для вокселов за поверхностью линейно убывает до нуля в пределах ε-окрестности. Такой выбор области определения весовой функции направлен на предотвращение возникновения ложных поверхностей.

В результате последовательной обработки всех видов каждому вокселю присваиваются значения интегральной функции расстояния D(Vi) (величина со знаком) и интегральной весовой функции W(Vi). Тогда построение изоповерхности D(Vi) = 0 и является решением нашей задачи. Преимуществом сведения исходной задачи к такой постановке является то, что построение изоповерхности скалярного поля, заданного на воксельной решетке, можно выполнить с помощью известного алгоритма марширующих кубиков.

Зашивка дыр

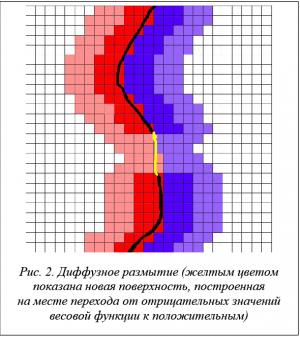
Для зашивки дыр в полученной единой модели применяется диффузное размытие значений неявной функции. Диффузное размытие необходимо для заполнения пустых вокселей значениями с соседних (непустых) вокселей, по этим значениям будет строиться новая поверхность (рис. 2).

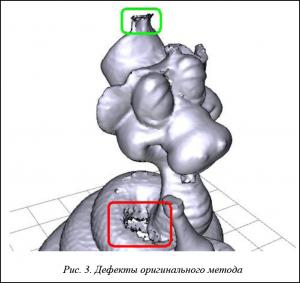
Сначала был реализован метод, предложенный в [4], но с использованием октодерева и оптимизации из [6]. Предполагалось, что такая реализация позволила бы сократить затраты памяти на порядок, что, в свою очередь, дало бы возможность повысить размерность воксельного пространства и таким образом повысить детализацию финальной модели при использовании того же объема оперативной памяти. Однако повышение детализации привело к невозможности зашивать большие дыры на модели за разумное количество итераций. Наряду с этим появились артефакты, связанные с ростом поверхности в неправильном направлении. Данный недостаток был описан в оригинальной статье [4]. На рисунке 3 показаны оба типа дефектов.

Для решения этой проблемы был предложен метод построения весовой функции вдоль не линии взгляда (рис. 4а), а нормали к каждому треугольнику (рис. 4б).

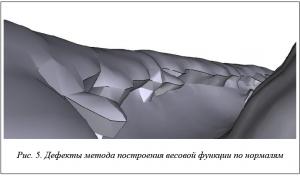
Такой метод позволяет избавиться от части артефактов, но порождает другие, возникающие в основном на больших перегибах поверхности (рис. 5). Объединение значений весовых функций обоих методов в одном пространстве значений также не дало желаемого улучшения.

Одновременно с проблемой «выростов» решалась и задача зашивки больших дыр. При небольшой размерности воксельного пространства дыры зашивались, но при увеличении размерности они переставали зашиваться даже при пропорциональном уве-личении количества итераций размытия. Поэтому было принято решение использовать при диффузии воксельное пространство меньшей размерности, а затем пересчитывать его на большее с учетом существующей поверхности. Был рассмотрен вариант использования верхних уровней октодерева. Анализ и эксперименты показали, что оптимальным является переход на четыре уровня октодерева (с уменьшением исходной детализации
в 4 096 раз). Именно на этом уровне проводится основное количество операций размытия, которые происходят на три порядка быстрее, чем на самом нижнем уровне октодерева. Затем осуществляется перенос зашитой поверхности с верхнего уровня на нижний. Это позволило решить проблему зашивки больших дыр, но осталась проблема «выростов». Поэтому был предложен гибридный метод, согласно которому поверхность строится на нижнем уровне методом «по взгляду», на втором уровне – по нормалям, далее производится диффузия на верхних уровнях, а затем поэтапно данные переносятся на более детальные уровни. Предложенный подход позволил избавиться от дефектов обоих типов.

Индексация треугольников

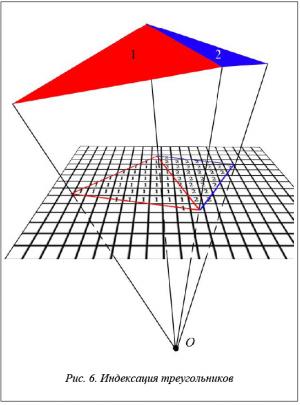
Заметим, что наиболее ресурсоемкой частью представленного выше метода является определение расстояний от вокселов до ближайшей поверхности при построении весовой функции. Вычислительная трудоемкость возникает из-за необходимости перебора всех треугольников с вычислением соответствующих расстояний. Чтобы избежать избыточных вычислений, предлагается механизм с предварительной индексацией всех треугольников сетки каждого вида (рис. 6). Для этого используется двумерный массив с размерностью, равной размерности изображения этого вида.

Тогда можно спроецировать каждый треугольник исходной сетки i-го вида на i-е изображение. В результате каждое значение массива приобретает либо индекс,
указывающий на принадлежность к определенному треугольнику, либо 0 – отсут-ствие проекции. Такая процедура возможна, поскольку исходная сетка для каждого вида является заведомо видимой, то есть не содержит невидимых на этом виде граней. Использование индексов при последующей работе алгоритма позволяет избежать полного перебора по всем треугольникам каждого вида и существенно уменьшает время работы алгоритма.

Текстурирование

Предварительная фильтрация.

Первая проверка – это проверка на наблюдаемость. Каждый треугольник построенной трехмерной модели проецируется на каждый из первоначальных видов. Для каждого из них рассчитывается угол наклона от нормали треугольника к линии, проходящей через центр камеры. Очевидно, если этот угол больше 90о, треугольник невидим и его можно отбросить. Для треугольников, у которых этот угол близок
к 90о, велика вероятность ошибки, но, если нет другого, более подходящего вида, эта проекция будет учтена и отбросится только в случае наличия лучшей альтернативы. Вторая проверка – это проверка на видимость, то есть на то, что наблюдаемый треугольник не перекрыт другими треугольниками этой модели. В общем случае потребовался бы перебор всех треугольников модели, что заняло бы значительное время. Для оптимизации можно воспользоваться уже построенной индексной картой для первоначальной модели. Для всех углов треугольника объединенной модели получим значения индексов треугольников исходных сканов до объединения. Если расстояние между этими объектами меньше порогового значения, значит, не существует объектов, которые загораживали бы рассматриваемый треугольник. Особняком стоят треугольники,
полученные в результате зашивки дыр: у них нет индексов на первоначальной индексной карте, поэтому проверять их на видимость придется с помощью полного перебора либо, если необходимо сэкономить время, использовать только критерий наблюдаемости. Логично, что для текстуры каждого треугольника нужно выбрать видимый участок, снятый с минимальным углом. Однако на стыках текстур, полученных с разных видов, появляются заметные границы (рис. 7а).

Попиксельное смешивание.

Основной проблемой при текстурировании трехмерной модели с помощью исходных фотоизображений является различное освещение на разных видах. На рисунке 8 видно, как один и тот же участок
поверхности модели выглядит по-разному на разных видах.

Решить эту задачу можно путем смешивания значений цвета для каждой точки текстуры с разных видов. Однако равномерное смешивание текстур приводит к не самым идеальным результатам (рис. 7б). Дело в том, что виды не равнозначны, поскольку на некоторых из них присутствуют сильные тени и пересветы, а на некоторых нужный нам треугольник снят под очень большим углом или находится на границе скана, где обычно могут быть ошибки сканирования. Поэтому было предложено использовать
гибридный вес для учета всех принятых критериев выбора текстуры по следующей формуле:

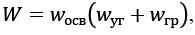                        (2)

где Woсв – вес по освещенности, функция имеет трапецеидальную форму, принимает значение 0 – для теней, затем линейно возрастает до 1 и так же линейно падает до 0 для пересветов;  – вес по углу наблюдения, линейно возрастает от 0 до 1 в зависимости от угла наблюдения;  – вес по расстоянию от треугольника до границы скана.

Если расчет первых двух параметров не вызывает трудностей, то расчет расстояния от каждого треугольника до границы скана в прямом виде является крайне ресурсоемким, поэтому была предложена следующая оптимизация. Уже существует построенная структура индексов для всех треугольников,
которая в двухмерном виде содержит индексы треугольников и нули там, где треугольников нет. Необходимо для каждого ненулевого значения вычислить расстояние до ближайшего нуля. Поскольку найденные значения использованы только в качестве веса, нет необходимости в вычислении абсолютных значений в 3d, достаточно вычисления дистанции на плоскости. Однако прямой перебор всех ненулевых значений и поиск ближайшего нулевого в заданном радиусе занимает продолжительное время – около 1,2 сек. на каждый вид. Поэтому была предложена следующая оптимизация. Каждому ненулевому значению индекса присваиваем максимальный вес, затем проверяем, есть ли рядом нулевое значение, если есть, добавляем в список и присваиваем значение 1. Затем будем производить поиск значений, равных максимальному весу, только в соседних ячейках элементов из этого списка. Такую итерацию производим необходимое число раз (рис. 9). Данная оптимизация позволяет сократить время вычисления веса в 6–8 раз.

На рисунке 10 показаны построенная для одного вида модели «Змея» (а) карта весов по дистанции от края скана (б), а также гибридная карта весов с учетом всех весов: по освещению, углу и расстоянию до края скана (в), рассчитанная по формуле (1).

Рассчитав вес для каждого пикселя, будем строить финальную текстуру. Для каждого пикселя каждого треугольника вычисляем цвет по формуле

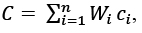                              (3)

где n – число видов;  – исходный цвет с i-го вида; должен быть нормирован так, чтобы сумма всех весов для всех видов была равна 1.

Результат текстурирования представлен на рисунке 7в.

Результаты

Для получения сравнительных оценок эффективности предложенного метода были проведены вычислительные эксперименты на реальных сценах, полученных с помощью трехмерного сканера RangeVision 3D (рис. 11–15). Параметры используемого вычислительного оборудования: процессор Intel Core i5 3,0 Ггц, 16 Гб оперативной памяти. Использование многоядерности позволило увеличить скорость работы в среднем в 2,5 раза по сравнению с однопроцессорным вариантом. Результаты экспериментов отражены в таблице.

Заключение

В работе представлен метод текстурирования триангуляционной трехмерной модели, построенной воксельным методом с зашивкой дыр. Тестирование на реальных данных показало, что предложенные алгоритмические решения и структура данных с использованием октодерева, индексации треугольников, вычисления гибридной весовой функции для каждого точки текстуры существенно повысили качество визуализации и производительность метода в сравнении с аналогами.

Литература

1. Ramamoorthi R., Arvo J. Creating Generative Models from Range Images. Proc. SIGGRAPH’99. 1999, pp. 195–204.
2. He X.J., Chen Y.H. A Haptics-guided Hole-filling System Based on Triangular Mesh. Computer Aided Design and Application. 2006, vol. 3, no. 6, pp. 711–718.
3. Jun Y. A piecewise hole filling algorithm in reverse engineering. Computer-Aided Design, 2005, vol. 37, no. 2, pp. 263–270.
4. Curless B., Levoy M. A volumetric method for building complex models from range images. Proc. SIGGRAPH’96, 1996, pp. 303–312.
5. Davis J., Marschner S.R., Garr M., Levoy M. Filling holes in complex surfaces using volumetric diffusion. First Inter. Sympos. on 3D Data Processing, Visualization, and Transmission, Padua, Italy. 2005, pp. 428–438.
6. Бобков В.А., Кудряшов А.П. Воксельный метод построения триангуляционной поверхности по множеству видов // Информатика и системы управления. 2012. № 2. С. 31–38.
7. Кудряшов А.П., Черкашин А.С. Построение единой триангуляционной поверхности по набору видов с зашивкой дыр // Информатика и системы управления. 2015. № 1. С. 36–40. 
8. Wei Zhao, Shuming Gao, Hongwei Lin. A robust hole-filling algorithm for triangular mesh // Intern. Jour. of Comp. Graph. 2007, vol. 23, iss. 12, pp. 987–997.
9. Podolak J., Rusinkiewicz S. Atomic volumes for mesh completion. Symposium on Geometry Processing, July 2005, pp. 382–391.
10. Kumar A., Shih A.M. Hole patching in unstructured mesh using volumetric diffusion. 19th Intern. Meshing Roundtable, Springer-Verlag, Research Note, 2010, pp. 228–237.
11. Gal R., Wexler Y., Ofek E., Hoppe H., Cohen‐Or D. Seamless montage for texturing models Computer Graphics Forum. 2009, vol. 29, no. 2, pp. 479–486.
12. Baumberg A. Blending images for texturing 3D models. Proc. BMVC, 2002, pp. 112–126.