Вопросы диагностики неполадок достаточно подробно рассмотрены в литературе для стационарных случаев эксплуатации объектов в условиях, близких к регламентным. При этом обычно используются методы, базирующиеся на статистических или эвристических представлениях. Подобный подход весьма эффективен в классе диагностики неисправностей как целевой функции. При создании систем управления широким классом объектов подобные подходы использовать затруднительно, рациональнее применять методы математического моделирования.
Формализованный подход к проблемам создания систем предотвращения развития потенциально опасных ситуаций зарекомендовал себя положительно на ряде предприятий [1]. Остановы по срабатыванию блокировок, вызванные неполным отказом оборудования, существенно снижаются. При этом программное обеспечение развивается в соответствии с возникновением новых задач, подлежащих решению. В этом заключается интенсивный путь развития производства, отличающийся от экстенсивного,
когда решение проблемы обеспечивалось за счет постоянного привлечения ресурсов, что не способствовало снижению затрат на поддержание режимов. Частичный отказ оборудования и нарушения технологических режимов можно предотвратить, делая упор на решение научных вопросов и предпринимая попытки общей компьютеризации системы управления.
Специфика диагностики состояний в химической технологии состоит в том, что диагностирование осуществляется в режиме рабочего функционирования без подачи на вход каких-либо тестовых или других воздействий. Многие параметры объекта, важные для оценки его текущего состояния, не могут быть непосредственно измерены.
В связи с этим необходимое условие для построения современной системы автоматического обнаружения и идентификации неисправностей – наличие математической модели, восполняющей недостающую информацию о диагностируемом объекте.
Основные требования, предъявляемые к моделям, – их достаточность для решения поставленных задач и удобство в использовании (практическая целесообразность). Так как диагностические модели являются весьма сложными и, как правило, критическими по времени, построение соответствующей модели оказывается проблематичным.
Современная постановка вопроса предполагает активное привлечение средств вычислительной техники как на этапе построения диагностической модели, так и во время ее непосредственной реализации, поэтому математическая модель должна быть машинно-ориентированной, предполагать активную обработку не только информации, имеющейся в банках данных и поступающей от объекта в ходе его эксплуатации, но и информации, априорно заданной в самой модели.
Модели, используемые в системах диагностирования, можно разделить на три группы: логические, причинно-следственные и аналитические [2]. Эти три типа моделей не являются альтернативными и могут быть использованы совместно.
Химические производства хорошо структурированы и в то же время характеризуются наличием агрегатов большой единичной мощности – аппаратов, в которых протекают сложные химико-физические процессы. Если технологическая схема рассматривается как совокупность последовательных участков, содержащих типовые устройства, целесообразно использовать логические и причинно-следственные модели. Но, когда объект невозможно расчленить на отдельные функционально взаимосвязанные узлы и для оценки его состояния необходим глубокий анализ происходящих процессов, используют аналитические модели.
Если объектом диагностирования является сложная химико-технологическая система (ХТС), возможно применение разнородных моделей, каждая из которых более удобна для решения частных задач. Создание единой всеохватывающей диагностической модели для целых технологических линий, по-видимому, не представляется возможным. Более эффективным следует признать подход, при котором из всей схемы выделяются ненадежные и потенциально опасные участки, чтобы диагностировать их с помощью простой и удобной в эксплуатации модели.
Логические модели для диагностирования непрерывных динамических систем
При диагностике технологического состояния непрерывных объектов широкое распространение получили методы, характеризующиеся тем, что о состоянии объекта судят по значению его контролируемых параметров. Результаты контроля параметров (говорят также о значении сигналов в контрольных точках) во многих случаях приводят к оценкам вида «в норме – не в норме», «в допуске – не в допуске» и т.п.
Для описания поведения непрерывных объектов, диагностирование которых осуществляется посредством анализа допусков, вполне естественно применять математические модели логического типа [3].
Нахождение параметра в допустимых пределах можно классифицировать как 1, а выход из заданной области – как 0. Подобным образом преобразуются как входные, так и выходные переменные объекта.
В конечном итоге задача диагностирования непрерывного объекта сводится к аналогичной задаче диагностирования дискретных объектов, элементы которых могут принимать логические значения «Да»–«Нет». При таком подходе появляется возможность использования глубоко изученных и достаточно давно применяемых на практике методов диагностирования цифровых схем [4, 5].
Объект диагностирования представляется в виде блоков Pi с вектором внешних входов xi, вектором входов yi, являющимися выходами предыдущих блоков объекта, и вектором выходных сигналов zi, части из которых могут быть входами последующих блоков.
Входы и выходы представляются множеством измеряемых параметров (контрольных точек), и полагается, что каждый из этих параметров может принимать лишь два значения: «в допуске», «не в допуске». Каждый блок Pi функциональной схемы заменяется абстрактными блоками Kj с одним выходом bij и существенными для выхода входами. При этом один и тот же входной сигнал может «расщепляться» на различные одновыходные блоки.
По выходу zij составляется булева функция Fij, которую можно записать в виде совершенной нормальной дизъюнктивной формы и затем минимизировать ее методами алгебры логики. На основе Fij строится таблица неисправностей [6].
Строки таблицы неисправностей составляет множество контрольных точек P={p1, ..., pn}, называемое также множеством попарно различимых проверок, а столбцы – множество попарно различимых состояний S={s1, ..., sm}. Элементом построенной таким образом таблицы является множество A={a11, ..., anm} результатов проверок aij, принимающих значения либо 1, либо 0, в зависимости от того, находится ли параметр pi в допустимых пределах в данном состоянии sj.
Логическая модель, заданная в виде таблицы неисправностей, позволяет с помощью специальных процедур нахождения минимального покрытия этой таблицы системой столбцов выбирать минимальное число контрольных точек для обеспечения различимости одиночных и кратных дефектов [7, 8] или, наоборот, доопределять минимальное множество точек контроля для возможного диагностирования неисправностей произвольной кратности [9].
В задачах диагностирования объектов химической технологии, как правило, используют не двух-, а трехзначное представление результатов измерений:
+ (плюс) – отклонение от области допустимых значений в сторону увеличения;
0 (ноль) – нормальное значение контролируемого параметра;
– (минус) – отклонение от области допустимых значений в сторону уменьшения.
Количество состояний таблицы неисправностей при этом составляет 3n, где n – число контролируемых параметров.
Число состояний может быть уменьшено, если для минимизации таблицы неисправностей использовать не только формальные, но и эвристические приемы, то есть основываться на имеющемся опыте и правдоподобных рассуждениях [10, 11].
В работе [12] решалась задача диагностирования участка димеризации олефинов, для чего было выделено семь трехзначных и пять двухзначных переменных. Полная таблица неисправностей составила 3725 =69984 различных столбцов состояний. Привлечение экспертных оценок позволило уменьшить число комбинаций до 51.
В работе [13] на простейшем примере буферной емкости, представленной четырьмя параметрами, подробно описана процедура построения таблицы неисправностей (по терминологии словаря неполадок, принятой в [13]) на основе эвристического подхода. Там же обобщены основные этапы составления словаря неполадок.
Эвристические методы применяются при построении не только логических, но и других типов моделей. Это обусловлено сложностью диагностических задач, их большой размерностью. Однако именно логические модели могут быть существенно эвристическими. Достаточно упомянуть простейшие и наиболее распространенные таблицы неисправностей, представленные таблицами различных инструкций и рекомендаций обслуживающему персоналу по действиям в условиях возникновения нарушений технологического процесса.
В настоящее время логические модели, заданные в виде таблиц неисправностей, имеют ограниченное применение, так как диагностируемые объекты, как правило, характеризуются большим числом параметров. Кроме того, при наличии обратных связей применение логических методов затруднительно. Но для диагностирования сравнительно несложных объектов логические модели в виде таблиц неисправностей, по-видимому, сохранят свое значение как наиболее простые.
Таблицы неисправностей являются также наиболее исчерпывающими и могут быть использованы на самых ответственных этапах построения других типов моделей, например причинно-следственных, когда важно не пропустить ни одной существенной детали и учесть даже маловероятные ситуации. Так, для автоматизации построения дерева отказов для ядерных реакторов (из-за высокой ответственности эта рутинная и в то же время требующая высокой квалификации работа обычно выполнялась вручную) в работах [14, 15] предложена методология, использующая таблицы решения, являющиеся более общим случаем таблицы неисправностей. Известны также методы обратного преобразования дерева отказов в булевы логические выражения [16].
Таблицы решений [17] более универсальны по сравнению с простейшими таблицами неисправностей, составленными по классификации «в допуске – не в допуске». Состояние контролируемой переменной может рассматриваться в терминах не двух- и трехзначной логики, а с любой произвольной градацией. Кроме того, для отражения динамики поведения объекта возможно разграничение переменных состояния по времени. Это значительно усложняет форму представления объекта диагностирования, однако, по мнению авторов [18], такое расширение функциональных возможностей значительно увеличит сферу применения этих моделей.
С широким внедрением в практику диагностирования современной вычислительной техники, использующей методы искусственного интеллекта, особое значение приобретают построение логико-лингвистических диагностических моделей [19] и применение небулевых логик [20]. Примерами использования аппарата нечеткой логики для диагностирования химико-технологических объектов могут служить работы [21, 22].
Причинно-следственные модели объекта диагностирования
Наиболее распространенными видами этой группы моделей являются помеченные направленные графы (ПНГ), деревья отказов (ДО) и деревья событий (ДС). Общим для причинно-следственных моделей является представление объекта в виде графа.
Каждый узел ПНГ ассоциируется с какой-либо переменной состояния объекта. Все текущие изменения переменных состояния учитываются не количественно, а качественно – посредством трехзначной логики в базисе значений +, 0 и –.
Дуга ПНГ, соединяющая два соседних узла, указывает на причинно-следственную связь между ними. Если изменение состояния исходного узла дуги вызывает такое же изменение конечного узла (такое же изменение знака), дуга помечается знаком +. Если же характер этого изменения обратный, дуга
помечается знаком –. Иногда для отражения скорости изменений вводят весовые коэффициенты +1, –1, +10, –10.
Известны также примеры введения в ПНГ фактора времени для отражения поведения объекта в динамике, учета задержек и т.п. [23–25]. Это важное дополнение, расширяющее информационные возможности ПНГ и в то же время существенно усложняющее его обработку. В работе [26] дополнительно введены также вероятности перехода из одного состояния в другое. Выбор той или иной модификации ПНГ зависит от особенностей решаемой задачи.
Помеченный направленный граф для трехэлементного объекта типа «входной поток – буферная емкость – выходной поток» изображен на рисунке 1. С увеличением расхода F1 входного потока уровень L в промежуточной емкости повышается, а с увеличением расхода F2 уменьшается. При повышении уровня L в емкости возрастает напор, и вследствие этого расход F2 увеличивается. При определении знака дуги, связывающей два узла, от всех остальных узлов абстрагируются, все внешние условия в расчет не принимаются.
Для одного и того же объекта могут быть составлены ПНГ различной сложности. Так, рассмотренный выше пример можно было усложнить с учетом возможных утечек как в трубопроводах, так и в самой емкости (разгерметизация корпуса, дефект в дренажной линии и т.п.). В этом случае дополнительными узлами были бы параметры давления. Можно сказать, что степень детализации модели зависит от постановки задачи диагностирования. В работе [27] для промежуточной емкости с регулируемым уровнем составлен ПНГ с 20 узлами и 33 дугами.
При диагностировании объекта, заданного в виде ПНГ, предполагается, что возникший дефект не является множественным, считается, что вероятность одновременного появления двух различных независимых дефектов пренебрежительно мала. Предполагается также, что возникший дефект возбуждает только один узел ПНГ, называемый корневым, и что он является единственным источником всех последовательно распространяющихся возмущений. В то же время этот дефект (корневой узел) не оказывает никакого влияния на не связанные с ним другие ветви ПНГ.
Основополагающим является допущение о том, что по причинно-следственной связи можно установить траекторию распространения нарушения и тем самым, наблюдая за изменениями состояний узлов ПНГ, выявить причину неисправности. Процедура диагностирования, таким образом, состоит в определении сильно связной ветви ПНГ, узлы которой инициированы отклонениями от номинальных значений. Тогда корневой узел этой ветви и будет дефектным источником нарушения.
Алгоритм выделения сильнодействующей, единственной по предположению компоненты ПНГ был предложен в работе [28] и затем получил свое дальнейшее развитие в работе [29].
Как правило, не для каждого узла ПНГ может быть определено его текущее состояние, и в общем случае в произвольный фиксированный момент некоторые узлы оказываются ненаблюдаемыми. Это может быть обусловлено тем, что часть переменных состояния объекта либо не измеряется по экономическим или техническим причинам, либо вообще не может быть измерена, так как эти переменные не являются физическими параметрами. Так, например, в ПНГ, составленном в работе [29] для сложной технологической схемы, из 99 узлов наблюдаемыми были 36.
Поэтому для соблюдения условия единственности решения необходимо соответствующим образом доопределить ненаблюдаемые узлы, назначить им знаковые метки. Разработанный алгоритм [29] формализует выбор доопределяемых узлов, определяет условия прекращения этой процедуры и устанавливает необходимость смены знака узла или другой корректировки метки. Для довольно сложного ПНГ, состоящего из 207 дуг, время диагностирования с использованием этого алгоритма не превышало 5 минут.
Необходимо иметь в виду, что диагностирование по ПНГ корректно только в том случае, если переменные состояния во время поиска дефекта изменяются лишь единожды вследствие возникшего нарушения [30]. Такое ограничение обусловлено тем, что ПНГ отражает только некий одномерный отклик системы на возмущение. Если еще до локализации дефектного узла компенсировать (например, регулирующим управляющим воздействием) или «поменять знак» реакции на возникшее возмущение какой-либо переменной состояния, то причинно-следственная связь диагностической модели будет нарушена.
Фиксированность времени и связанная с ней фиксированность переменных состояния – недостаток, характерный не только для ПНГ. Он присущ практически всем причинно-следственным моделям и связан с тем, что диагностируемый объект, который является непрерывной динамической системой (или непрерывно-дискретной), представляется дискретной моделью. В тех случаях, когда такое упрощение не позволяет решать поставленные задачи, используют различные модификации ПНГ: вводят фактор времени (см. выше) или учитывают множественность состояний ПНГ [31].
Естественным выходом из этого затруднения было бы сведение времени диагностирования до нескольких секунд, а в критических случаях и до миллисекунд. Поэтому дальнейшие исследования были направлены на повышение быстродействия, но не путем совершенствования алгоритмических процедур, а путем преобразования ПНГ в расширенное множество логических правил, имеющих своей целью формирование четких инструкций.
Как отмечалось в работе [32], для химических производств число таких правил может составлять десятки тысяч. Это связано не только с тем, что химические производства, как правило, сложные и достаточно структурированные объекты. Причинно-следственные модели из-за своего качественного, а не количественного характера неоднозначны и определяют целое множество возможных логических правил.
Число интерпретаций ПНГ зависит от числа контуров обратной связи. Если последнее равно N, то число возможных конфигураций равно 2N [30]. Если в i-й узел ПНГ сходятся ni дуг, то число возможных интерпретаций умножается на ni. Например, если в ПНГ (без учета обратных связей) имеются 5 узлов с двумя и 2 узла с тремя сходящимися дугами, то общее число возможных представлений в виде логических правил составит 2532=288.
Для исходного обобщенного ПНГ (рис. 2) можно записать логическое правило:
Если {(pAB)Ç(pAC)Ç(pCE)Ç[(pBD)È(pCD)]Ç [(pD)È(pE)]}, то A=+1 есть возможный дефект. Здесь логический оператор p определяется как (pAB)«(A=B)Ç(|A|>|B|); Ç – логическая функция И (конъюнкция); È – логическая функция ИЛИ (дизъюнкция); « – логическая функция эквивалентности. Аналогично можно ввести операторы: (mAB)«(A = –B)È È(|A|>|B|), (zAB)«(B=0). Если выбор логического оператора (p, m или z) не определен, а зависит от особенностей эксплуатации, то можно использовать обобщенный оператор (xAB), дополнительно оговаривая, при каких условиях какое значение он приобретает.
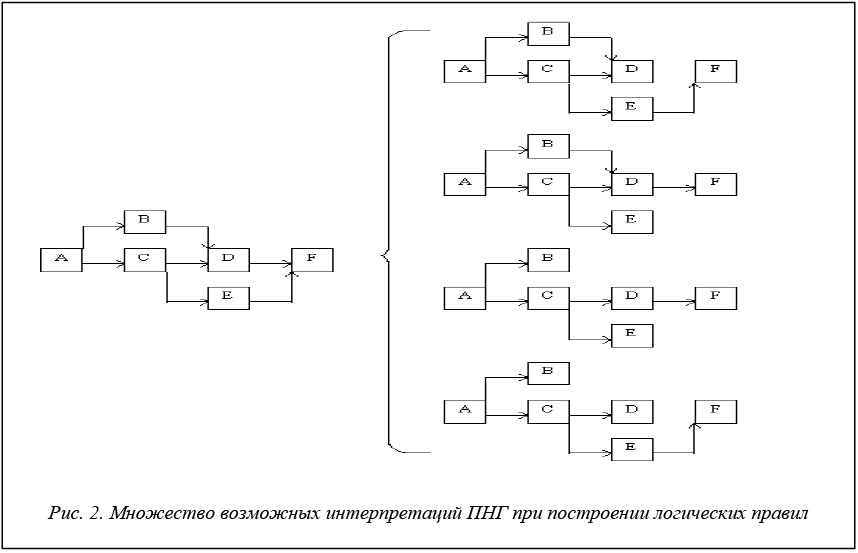
В работе [30] в качестве объекта диагностирования рассматривается экзотермический реактор с рециклом. Логические правила строились для случая возникновения дефекта регулятора уровня. Эта модель содержала 647 различных комбинаций, и обработка на IBM PC требовала менее 2 секунд [30].
Также представляет собой интерес концепция иерархического диагностирования [33].
На глобальном уровне используемая модель может быть не детализирована, однако она должна обеспечить локализацию неисправности с точностью до подсистемы нижнего уровня иерархии. На втором этапе с помощью соответствующих процедур дефектная область сужается уже до размеров неисправности элемента.
При этом возникает проблема соотнесения элемента схемы с тем или иным классом общности, так как сосуществуют два взаимосвязанных аспекта [34]: структурный, определяющий физическое местонахождение объекта, и функциональный, определяющий группировку элементов по их функциональному назначению и взаимосвязанности поведения.
В работе [35] доказывается необходимость совмещения структурной и функциональной моделей сложной системы в рамках решения одной задачи. Предлагается методология автоматизированного диагностирования сложных цифровых схем, модель которых сочетает как структурные, так и функциональные элементы. Однако в общем случае затруднительно выделить функциональную зависимость из структурных представлений. Часто один и тот же структурный элемент выполняет различные независимые функции. Например, забивка трубы с охлаждаемой средой в теплообменнике не влияет на функционирование охлаждающей среды в межтрубном пространстве.
Структурно-функциональный подход может быть использован для иерархического диагностирования, когда на первом этапе при довольно высоком уровне общности первоочередной является функциональная информация, и лишь затем требуется детализация структуры с точностью до элемента.
Исходя из этих соображений в работе [35] была предложена процедура построения причинно-следственной модели. В работе [36] эта идея получила дальнейшее развитие. Более конкретно ее можно представить следующим образом.
Отдельные элементы объекта, имеющие узкое целевое назначение, могут быть функционально объединены в группы, ориентированные на выполнение какой-либо более общей задачи, на достижение целей более высокого уровня. Эти глобальные цели можно назвать системными, а группы, образованные по функциональному признаку, подсистемами объекта. Исправность подсистемы в этом случае определяется тем, как она выполняет системную задачу.
Таким образом, объект подразделяется на подсистемы S1, ..., Sk, каждая из которых может быть представлена уже не структурными единицами, а функционально – как множество определенных функций отдельных элементов схемы. При этом одна и та же j-я функция i-го элемента Uij может входить в различные функциональные группы, то есть некоторые подсистемы объекта могут иметь непустое пересечение SnmÇSm=Uij.
Одна подсистема считается зависимой от другой, если выполнение функционального назначения первой зависит от исправности второй.
На начальном этапе диагностирования отвлекаются от внешней структурной зависимости между подсистемами и изучают внутреннюю функциональную зависимость через общие функциональные элементы. Задача нахождения источника дефекта, элемента подсистемы диагностируемого подграфа, аналогична задаче нахождения корневого узла в ПНГ, где требовалось выделить узел – переменную состояния объекта, непосредственно подверженный воздействию дефекта от тех узлов, которые перешли в ненормальное состояние в результате причинно-следственной связи с дефектным узлом. Здесь же требуется выделить подсистему, возбудившуюся из-за возникновения дефекта в одном из ее функциональных элементов.
Отличие функционального графа от ПНГ состоит в том, что в момент возникновения дефекта возбуждаются все те узлы, в которых содержится дефектный функциональный элемент. Так как один и тот же дефектный функциональный элемент может одновременно входить в различные подсистемы, то, продолжая сравнение с ПНГ, это равносильно множественному дефекту, который в ПНГ, как правило, вообще не предусматривается.
Выделение функциональных элементов диагностируемого объекта, их группирование в подсистемы, составление таблицы внутренних взаимосвязей и построение графа внешней взаимосвязи – все это осуществляется на стадии проектирования. Поэтому все приведенные рассуждения легко формализуются по составленным таблицам. В отличие от ПНГ, где могут использоваться переменные состояния, недоступные для прямого наблюдения, все узлы функционального графа являются наблюдаемыми, и при возникновении дефектных отклонений диагностический подграф выделяется автоматически.
Согласно работе [36], после первой стадии, заканчивающейся выделением из функционального графа диагностического подграфа, наступает второй этап – дальнейшее сужение множества возможных источников дефекта посредством диагностических правил.
Диагностические правила имеют обобщенный вид, их количество не зависит от сложности объекта и будет сравнительно небольшим. Появляется возможность компактной систематизации этих правил в соответствующие таблицы. Используя их, оператор будет получать рекомендации, значительно сужающие область поиска дефекта.
Графовые модели отличаются наглядным представлением диагностируемого объекта. Роль модели как раз и состоит в наиболее удобном задании априорной диагностической информации, с тем чтобы впоследствии, а именно в режиме реального времени, с помощью специальных алгоритмов конкретизировать эту информацию применительно к возникшей ситуации.
Граф-модели позволяют решать весьма сложные диагностические задачи [37, 38] и не ограничиваются только помеченными орграфами, хотя последние уже давно используются для диагностирования химико-технологических объектов и в этой области накоплен большой опыт [39].
Для решения сложных задач, когда последовательность событий, происходящих при возникновении неисправности, зависит от множества условий и заранее не может быть определена однозначно, а также в тех случаях, когда необходимо учитывать динамику поведения объекта, целесообразно использование сетей Петри и различных их модификаций. Сети Петри используются в основном для моделирования сетей массового обслуживания и активно взаимодействующих и сильно связных многокомпонентных дискретных систем. Известны примеры, когда сети Петри используются для анализа связных деревьев отказов [40], но могут применяться и самостоятельно для решения сложных диагностических задач [41–44]. Сети Петри также являются помеченными направленными графами, однако в отличие от ПНГ они используют элементы пороговой логики и их метки являются динамическими. Из обзорных работ, посвященных сетям Петри, следует отметить [45].
В последнее время заметно возросло число публикаций по использованию в задачах диагностики пороговых логических графов – нейронных сетей. Отличительной особенностью нейронных сетей является их адаптивность, поэтому они могут быть использованы в тех случаях, когда неизвестна корреляция между переменными процесса. Возможность обучения на действующем процессе исключает необходимость точного знания степени влияния одних переменных на другие. Это свойство нейронных сетей делает их весьма перспективными для использования в системах распознавания предаварийных и аварийных состояний объекта. Вопросам практического применения нейронных сетей для диагностирования процессов химической технологии посвящены работы [46–51].
В одной из обзорных работ [52], посвященных диагностическим моделям, кроме ПНГ, рассматриваются такие причинно-следственные графы, как схемы влияния и логические потоковые графы.
Схемы влияния были впервые предложены в 1976 г. сотрудниками Станфордского исследовательского института для формального описания процессов принятия решения. Существуют различные варианты схем влияния. В некоторых случаях они представляют состояние параметров процесса, а дуги – качественную связь между ними. В других модификациях узлы обозначают повышенный уровень соответствующих количественных характеристик условий ведения процесса, а дуги показывают существующую взаимосвязь между ними. По схемам влияния составляют матрицы достижимости, которые, в свою очередь, могут быть сведены к прямым или интуитивным процедурам поглощения узлов и инверсии дуг. Наибольшее применение схемы влияния получили в задачах анализа гибких автоматизированных производств.
Логические потоковые графы более сложные, они нашли применение для моделирования и диагностирования неисправностей в ядерных реакторах [53, 54]. Потоковые модели могут быть также использованы для контроля за состоянием процесса по уравнениям материального и энергетического балансов [55, 56].
С помощью этого типа графов можно представлять причинные петли, нелинейную взаимосвязь между параметрами процесса, резкие изменения условий ведения процесса, так как дискретизация параметров может быть осуществлена таким образом, что будет учитывать весь спектр возможных изменений. Помимо обычных для графовых моделей причинно-следственных связей, используются также формальные условия, указывающие, каким образом и при каких логических управляющих воздействиях эти причинно-следственные связи изменятся. Предусмотрен механизм выделения интересующих комбинаций условий и дефектов по поступающей в режиме реального времени измерительной информации или по указаниям оператора.
Можно сказать, что ПНГ по своим функциональным возможностям занимают промежуточное положение между схемами влияния и логическими потоковыми графами. Однако ПНГ позволяют легко переходить к логическим правилам типа «если–то», поэтому нашли большее применение.
Наиболее распространенную группу причинно-следственных моделей составляют ДО, которые синтезировали текстовое, логическое и графовое представления объекта диагностирования.
Модели ДО широко рассматриваются в научной литературе. Хотя концепция ДО была сформулирована в середине 60-х гг. при выполнении исследовательских работ по диагностированию систем запуска баллистических ракет «Минитмен», основной вклад в развитие этого подхода внесли многочисленные ведомственные отчеты по безопасности ядерных реакторов (например [57]).
Большое внимание уделено ДО также в [13, 18, 58, 59]. Из современных обзорных работ следует отметить [60, 61]. В первой из них указаны наименования и литературные источники машинных программ, реализующих данный метод, во второй систематизированы обозначения, методы анализа и даны четкие определения для различных типов ДО.
Основные ограничения и затруднения, присущие методу диагностирования с помощью ДО, обсуждаются в работах [62, 63]. Учет неопределенности во входных данных и множественность состояний рассматриваются в работах [64–68]. Примеры нетрадиционного применения ДО приведены в [69–72].
ДО правильнее определять не как причинно-следственную, а как следственно-причинную модель, подчеркивая тем самым ее дедуктивность. Продвижение по ДО осуществляется от зафиксированного дефекта (события в вершине) к возможной причине, вызвавшей этот дефект (к исходному событию).
Событие, определенное на каком-либо шаге как возможная причина, на следующем шаге анализа рассматривается уже как следствие. Такое последовательное выделение промежуточных результатов выполняется до тех пор, пока не будет пройдена вся цепочка событий, образующая ветвь ДО.
Построение ДО для сложных и ответственных объектов – трудоемкая процедура, первые алгоритмы формализованного получения ДО из структурного представления объекта были предложены уже в начале 70-х гг. При этом можно выделить два подхода конкретизации причинно-следственных связей при возникновении неисправности.
В работе [73] каждый элемент технологической схемы представляется соответствующей функцией распространения неисправности. Например, для участка трубопровода (аналогично для запорной арматуры, местного сопротивления и т.п.) составляются функции вида
Fвых = f (Pвх – Pвых).
Эта элементарная модель отражает тот факт, что расход выходного потока Fвых увеличивается с возрастанием перепада давлений, то есть если повышается давление Pвх на входе или понижается давление Pвых на выходе.
По таким функциональным моделям, поясняющим качественную зависимость между основными параметрами, характеризующими элемент схемы, составляются мини-деревья отказов.
Полное ДО из таких мини-деревьев на стадии проектирования не синтезируется, но если в процессе эксплуатации объекта случается какое-либо отклонение процесса от нормы, то это дерево начинает расти, исходя своей вершиной из элемента (мини-дерева), соответствующего признаку данного нарушения. Сочленение осуществляется автоматически по общим для различных мини-деревьев компонентам, исключая противоречивые ситуации [74–76].
Подробно процесс формирования диагностического подграфа ДО из мини-дерева изложен в работе [77]. Там же рассматривается и другой подход.
В отличие от процедуры наращивания диагностической модели в момент возникновения дефекта другая группа методов вычленяет из полного ДО, составленного на стадии проектирования, интересующую ветвь. Дерево отказов составляется, как и в предыдущем случае, на основе элементарных функциональных моделей. Они также имеют качественный характер, но являются более полными. Например, рассмотренное выше модельное уравнение участка трубопровода может быть дополнено следующим образом: dPвх/dt = f (Fвх – Fвых). Последнее уравнение указывает на то, что скорость изменения давления на входе Pвх возрастает с увеличением расхода входного потока Fвх и падает с увеличением выходного потока Fвых
Если в процессе эксплуатации появляется признак неисправности какого-либо элемента, то исходная полная модель, составленная для всей схемы, редуцируется до дефектного элемента с сохранением
только тех взаимосвязей, которые имеют к нему непосредственное отношение. Этот упрощенный диагностический подграф и анализируется специальными алгоритмами, рассмотренными, например, в работах [77, 78].
Были предложены различные машинно-ориентированные методы построения ДО. Например, использованию таблиц решений в дополнение к уже упоминавшимся [14, 15] посвящены работы [79–81].
Как отмечалось в работе [82], эти методы во многом близки к построению ДО по мини-деревьям. Большое число работ посвящено построению ДО по граф-моделям, например, по так называемым причинно-следственным диаграммам [83–85] или по графам надежности [86, 87]. Известны также промежуточные графотабличные алгоритмы [88, 89].
Но для диагностирования химических производств наибольшее распространение получили алгоритмы автоматизированного синтеза ДО, построенные на основе ПНГ. Впервые такой алгоритм был изложен в работе [90]. Эта и ряд последующих работ [91–94] вызвали активное обсуждение в печати [95–98]. Интерес к этой проблеме не ослабевает и в нынешнее время. Из работ последних лет можно отметить [99–104]. Подробнейшее изложение метода на примере объекта химической технологии приведено в цикле из нескольких работ [105, 106].
Основной недостаток диагностирования с использованием ДО (как и для всех причинно-следственных моделей) состоит в двумерности представления переменных состояния, а также в сложности моделирования обратных связей [52, 63, 107–109].
В работе [110] влияние поведения отдельных компонент объекта на переменные процесса, включая возможные задержки ответной реакции, систематизировались в виде индивидуальных таблиц решений. Таблицы составлялись для всех возможных дискретных входов данной компоненты и для всех ее состояний. Для устранения ограничений, присущих причинно-следственным моделям, то есть для возможности решения задачи диагностирования неустановившегося состояния объекта с контурами обратной связи, использовался принцип «сочетание критических переходов». Посредством специально разработанных вычислительных алгоритмов базы данных, составленные в виде таблиц решений, обрабатывались, чтобы учитывалась зависимость внутренних состояний объекта от последовательности событий [18].
Для этих целей используются [111] параметрические зависимости между состояниями каждой компоненты, составленные таким образом, чтобы можно было установить переменные процесса, заданные в виде алгебраических или дифференциальных уравнений. Эти параметрические зависимости связываются с драйвером – программой, управляющей моделированием поведения системы при изменении во времени состояний ее компонент. По имеющимся данным, драйвер генерирует последовательность событий, по которой вычисляется их возможное распределение для каждой вершины дерева.
В работе [112] по дифференциальным уравнениям процесса и по данным об отдельных компонентах строится цепь Маркова, которая и является рабочей моделью, описывающей вероятностное поведение системы с обратной связью в дискретные моменты времени. Это направление в последние годы активно развивается.
При выходе из строя важного узла или при наличии какого-либо другого явного отказа очень важно иметь возможность оперативного прогнозирования развития аварийной ситуации, оценки ее последствий. Таким образом, возникает задача, обратная построению ДО.
Если при анализе и синтезе модели конечный результат – выявление отказа или какого-либо повреждения, а исходный – некое проявление этого дефекта в том или ином событии, то речь идет о ДО. Если исходным является возникший или возможный дефект и причинно-следственные связи устанавливаются с целью определения последовательности следующих за этим дефектом событий, то говорят о ДС.
Первая модель, уже достаточно подробно рассмотренная, следственно-причинная (дедуктивная), вторая – причинно-следственная (индуктивная).
Разновидностью ДС является дерево решений. В ДС рабочие состояния не рассматриваются, так что суммарная вероятность всех событий, представленных в ДС, не равна единице. В дереве решений через состояния его элементов учитываются все возможные состояния объекта диагностирования, в том числе и исправные [18].
В работе [113] ДС было использовано для совершенствования защиты от неисправностей, возникающих в химических производствах. Дерево событий позволяет заранее проанализировать и систематизировать информацию о возможных неисправностях, об условиях, ускоряющих их развитие и повышающих частоту их появления. Это позволяет не только оперативно действовать в критической ситуации, но и правильно организовывать необходимые профилактические меры по ее предупреждению [114].
В последнее время широкое распространение получила методика HAZOR (hazard and operability study – «опасность и изучение действенности») [115]. Эта методика заключается в комплексном изучении отклонений технологических параметров от номинальных значений, то есть в качестве исходного дефекта рассматривается не отказ, а повреждение. В соответствии с действующим стандартом [116] отказом является нарушение работоспособного состояния, а повреждением считается событие, заключающееся в нарушении исправного состояния объекта при сохранении его работоспособности. При этом для каждого рассматриваемого отклонения режимных параметров последовательно изучаются как возможные причины, так и возможные последствия [117].
Такой подход выдвигает качественно новые, более жесткие требования к разработке системы диагностирования, так как ставится задача распознавания и обработки информации о только зарождающемся нарушении, когда процесс еще находится в устойчивом и работоспособном состоянии, но в нем уже присутствуют негативные тенденции.
Если в работе [118], где систематизировалась процедура HAZOR, общий подход можно охарактеризовать как качественный анализ объекта, то обзор [119] посвящен проблеме количественного анализа риска (так называемая методика QRA – quantitative risk analysis). Разработаны также методы количественно-качественной оценки объекта (процедуры FRR – facility risk review) [120]. Однако наибольшее внимание исследователей привлекает HAZOR. Этот подход изучается давно [121–125] и постоянно совершенствуется. HAZOR можно использовать для построения ДО [126, 127].
Как уже отмечалось, в HAZOR для исследуемых отклонений параметров последовательно анализируются и возможные причины, и возможные последствия. Это указывает на возможность выделения диагностической модели, промежуточной между ДО и ДС, а точнее, объединяющей оба подхода. Такой
моделью является причинно-следственная диаграмма [13, 18], и выше уже отмечалась возможность построения на ее основе ДО [83–85].
Основным достоинством причинно-следственных диаграмм является возможность представления последовательности событий, так как наряду с блоками, типовыми и для ДО, предусматриваются также элементы задержки, особенности построения которых приведены в работах [13, 128].
Рассмотренные причинно-следственные модели крайне редко используются обособленно. Для каждой из них характерна тесная взаимосвязь с другими формами причинно-следственного представления объекта, что выражается в комплексном применении моделей этого класса на различных этапах построения диагностической модели. Как правило, в качестве рабочей модели используют ДО, а некоторые другие причинно-следственные модели, например ПНГ или таблицы решений, являются вспомогательным средством представления объекта на начальной стадии формирования ДО.
Причинно-следственные модели являются проблемно-ориентированными и могут быть использованы на всех этапах диагностирования – от обнаружения неисправности до принятия соответствующего решения. Однако эти модели действенны только для тех объектов, которые можно представить совокупностью взаимосвязанных компонент, при этом состояние каждой из них может быть определено либо как исправное, либо как неисправное.
Существенным недостатком причинно-следственных моделей является то, что для их построения необходим подробнейший разбор всех возможных ситуаций. Это предполагает исчерпывающее знание особенностей поведения объекта в тех или иных условиях, наличие количественных характеристик надежности отдельных элементов, необходимых для принятия решения в недетерминированных случаях. Однако, как показывает практика [129], наиболее тяжелые последствия обусловлены возникновением наименее вероятных и поэтому заранее не предусмотренных событий. Такие ситуации практически невозможно учесть на стадии проектирования, то есть на этапе построения модели. Особенно проблематично это для сложных и малоизученных объектов. Если это и возможно, то чаще всего экономически нецелесообразно. Они, как правило, ограничиваются наиболее вероятными дефектами.
Модели в пространстве состояний
Аналитические модели также могут рассматриваться как причинно-следственные: свойство причинности характерно для всего класса динамических систем, у которых выделены входные и выходные переменные. При этом событиями-следствиями полагаются выходные реакции объекта, а причинами – вызвавшие их входные воздействия. Однако в уравнениях эта причинно-следственная связь задана неявно.
С другой стороны, переменные состояния не всегда имеют ясный физический смысл и не всегда могут быть измерены. Часто это гипотетические переменные, вводимые для отражения изменений условий функционирования объекта, а также для упрощения вычислений. В этом случае связь математического описания с физической реальностью теряется, расчеты нельзя сопоставить с физическими представлениями. Поэтому метод пространства состояний следует рассматривать как общую методологию, позволяющую решать очень широкий спектр задач, многие из которых либо затруднительно, либо невозможно решить классическими методами.
Модель в пространстве состояний является наиболее полной и наиболее универсальной. Она легко может быть расширена для решения специальных задач или сведена к какому-либо другому виду моделей. Так, например, в монографии [130] пространство состояний непрерывной динамической системы представляется в виде направленного причинно-следственного графа. Известны также примеры преобразования дерева отказов в эквивалентные диаграммы пространства состояний [131].
Однако наибольший интерес представляют алгоритмы перехода от передаточных функций к модели в пространстве состояний и наоборот, поскольку одни методы анализа и синтеза систем проще реализуются во временной области, другие – в частотной.
Интересные перспективы открываются в связи с разработкой нового подхода, при котором основой для построения динамической модели передаточной функции или уравнений в пространстве состояний являются не дифференциальные уравнения с назначаемыми входными и выходными переменными, а временные ряды.
Согласно этому подходу, в статье [132] динамическая система определена в самом общем виде – как произвольное семейство траекторий в фазовом пространстве. В такой формулировке понятия линейной стационарной системы типа «вход–выход» и типа «вход–состояние–выход» по существу эквивалентны и могут моделироваться линейными уравнениями, представляющими семейство временных рядов:
Rw(t) + R1w(t+1) +...+ RSw(t+s)=0, (1)
где w = (u, y), то есть выходы и входы не различаются и могут быть заданы неявно; R, ..., RS – коэффициенты семейства временных рядов. Модель вида (1), записанная с убывающей индексацией, широко известна как AR-модель.
В работе [133] приведены алгоритмы получения (1), реализующего заданное поведение объекта, а также получения модели в пространстве состояний, эквивалентной (1). Рассматриваются также вопросы получения модели в пространстве состояний непосредственно по результатам наблюдений. Такая методология позволяет рассматривать не точные, а приблизительные модели, достаточные для решения
поставленной задачи. Так, предлагаются алгоритмы вычисления оптимально подобранной модели с максимально допустимой сложностью или, при ином подходе, алгоритмы для вычисления минимально сложной модели, которая объясняет наблюдаемый временной ряд с точностью до максимально допустимой несогласованности.
Эти результаты в работе [134] были распространены на системы, функционирующие в непрерывном времени и описываемые нелинейными дифференциальными уравнениями. Предложены достаточные условия и процедуры, позволяющие реализовать системы от внешних переменных (в которых не произведено разделение на входы и выходы) в виде систем типа «вход–состояние–выход».
Эти исследования только начаты и пока еще не получили инженерную апробацию. Что касается метода пространства состояний в традиционной постановке, то он уже давно и весьма успешно применяется на практике.
Специфика задач функциональной диагностики динамических объектов требует, чтобы рабочая модель отражала не только номинальные значения параметров, но и условия, в которых эти параметры определяются. Преимущество моделей в пространстве состояний как раз и состоит в том, что они могут быть сравнительно легко расширены без усложнения своей структуры.
Пусть, например, необходимо учитывать неконтролируемые возмущения, воздействующие на объект, которые влияют на выходы независимо от входных управляющих воздействий. Такого рода возмущения называются аддитивными нарушениями процесса [135], к ним можно отнести, например, течи, вызванные разгерметизацией рабочих емкостей.
Другой тип аддитивных нарушений вызван несоответствиями входных и выходных переменных объекта их действительным значениям. Дефекты такого рода отражают не только систематические погрешности измерительных приборов и неисправности датчиков, но и сбои в работе исполнительных механизмов. Последние можно рассматривать как несоответствие предполагаемого вычисленного управляющего воздействия реально реализованному исполнительным механизмом.
Пусть эти два типа аддитивных нарушений обозначены соответственно векторами v(t) и w(t). Тогда расширенное уравнение динамики в пространстве состояний примет вид
x•(t) = Ax(t) + Bu(t) + Dv(t) + Ew(t).
Аналогично можно определять вход–выходное уравнение:
F(p)y(t) = G(p)u(t) + H(p)v(t) + J(p)w(t).
Здесь G(p) и F(p) – соответственно числитель и знаменатель передаточной функции W(p), а D, E, H(p) и J(p) – матрицы коэффициентов соответствующих размерностей, причем в частотной области они заданы в операторной форме (р – оператор Лапласа).
Для учета аддитивных дефектов первой группы по приведенной выше классификации вводят векторы Du(t) и Dy(t), а для учета дефектов другой группы – векторы du(t) и dy(t). Тогда контролируемые входы и выходы будут представлены следующим образом:
u~(t) = u(t) + Du(t) + du(t), y~(t) = y(t) + Dy(t) + dy(t).
Матрицы коэффициентов также уточняются введением в их выражения переменных, которые учитывают несоответствие используемой модели действительным значениям параметров: A^=A+DA(t), B^=B+DB(t), C^=C+DC(t), F^=F(p)+DF(p,t), G^=G(p)+DG(p,t). Такое представление матриц коэффициентов позволяет отразить в модели те дефекты, которые невозможно выделить в независимые слагаемые. Если последние определяются как аддитивные, то данную группу нарушений можно вызвать мультипликативными дефектами. К ним можно отнести резкие или постепенные изменения параметров объекта, например, воздействие полного или частичного отключения электроэнергии, ухудшения теплообмена из-за осаждения на стенках аппарата, старение катализатора и т.п.
Теперь, если обобщить, сгруппировав векторы переменных и матрицы коэффициентов q(t)={uT(t),yT(t)}, K(p)=[G(p),-F(p)], то в исправном состоянии (v(t)=0, w(t)=0, DF(p,t)=0, DG(p,t)=0) выполняется условие K(p)q(t)=0. В общем случае при возникновении неисправности
K(p)q(t)=[K^(p)dq(t)-J(p)w(t)]+[K^(p)Dq(t)-H(p)v(t)]+DK(p)q(t).
Здесь первое слагаемое соответствует аддитивным нарушениям системы управления, второе – аддитивным нарушениям процесса и третье – мультипликативным нарушениям. Маловероятно, чтобы все эти дефекты возникли одновременно, но приведенное уравнение отражает самый неблагоприятный случай.
Важно отметить, что, несмотря на определенное разграничение дефектов группы, все они взаимосвязаны. Например, течь, вызванная повреждением корпуса аппарата, являясь аддитивным нарушением процесса, зависит также и от давления, которое является мультипликативным параметром. С другой стороны, нулевой выход в каком-либо канале измерения может быть отнесен как к аддитивным дефектам системы управления (отказ датчика), так и к мультипликативным нарушениям процесса (изменение соответствующего параметра до нуля).
Что касается трансформации модели в пространстве состояний, то для сохранения их структуры достаточно соответствующим образом определить вектор переменных состояния, который так или иначе выбирается произвольно, исходя из соображений целесообразности и удобства.
Так, например, в работе [136] решалась задача стабилизации ректификационной колонны – сложного нелинейного объекта с распределенными параметрами. Обычное управление по модели, заданной в виде передаточной функции, не дало удовлетворительных результатов, хотя были испробованы самые различные схемы, в том числе с использованием m-оптимальных и многосвязных Пи-регуляторов. Объект оставался неустойчивым, что приводило к частым аварийным остановам и, как следствие, к большим потерям.
Задача решалась в дискретном представлении. Из матричной передаточной функции (также дискретной, заданной в виде z-преобразования) была получена модель. Затем она модифицировалась таким образом, чтобы можно было учесть все возможные возмущения, воздействующие на объект. Оказалось, что вполне применим стандартный подход с использованием пространства состояний, дополненный хорошо известными методами оценивания состояний. Для этого был введен вектор ошибки оценивания, который играл такую же роль корректора, как и сигнал обратной связи в обычных информационных управляющих структурах. Заданное качество управления было полностью обеспечено. Расширенный вектор состояния имел вид
xm(k)={x•(k|k‑1),x,u(k-1)}.
Здесь x•(k|k-1) – оценка состояния x в момент k, вычисленная по информации, имеющейся в предыдущий (k-1)-й момент. Вектор управлений также был расширен вектором установок регулятора, сигналом обратной связи и вектором контролируемых возмущений.
В работе [137] решалась еще более сложная задача диагностирования нелинейной нестационарной стохастической системы – проточного емкостного реактора с перемешиванием и теплообменом, в котором протекает реакция второго порядка типа 2А®B.
По уравнениям материального и теплового баланса была составлена модель в пространстве состояний четвертого порядка. В качестве переменных состояния выбраны концентрация исходного реагента, температура в зоне реакции, температура окружающей среды и температура поверхности охлаждения, но не абсолютные значения, а отклонения от номиналов, эталонных в условиях нормального функционирования значений.
Модель задавалась в виде
x(t)=(A+QDA)x(t)+(B+QDB)u(t)+Ew(t),
x(0)=x,
y(t)=Cx(t)+v(t),
y(t)=(С+DC)x(t)+g(t)+v(t).
Здесь приняты следующие обозначения: w(t) – вектор шумов процесса; v(t) – вектор шумов в измерениях; g(t) – вектор неисправностей; Q – постоянная матрица коэффициентов нелинейной части модели процесса; E – постоянная матрица коэффициентов линейной части процесса; DA – матрица, элементы которой являются функциями от времени, а возможно, также и от векторов x(t) и u(t); DB – матрица, элементы которой являются функциями от времени и, возможно, от вектора u(t); DC – изменение матрицы C, вызванное нарушениями в системе; нижний индекс 0 означает исправные составляющие.
Компоненты QDAx(t) и QDBu(t) характеризуют неопределенность системы, связанную с нестационарностью, неизвестными составляющими, а также с неопределенностью коэффициентов модели, заданных на стадии проектирования. Эта часть уравнения динамики системы рассматривалась отдельно. Для диагностики нарушений также использовались методы оценивания состояний [135, 138, 139].
Алгоритмы оценивания состояния объекта, подверженного случайным возмущениям, рассматривают различные помехи как белый шум, случайный процесс с нулевым средним и с независимыми, сколь угодно близкими координатами. В условиях практической эксплуатации эти шумы являются цветными с той или иной степенью корреляции. Если по условиям процесса они не могут приближенно полагаться белыми, то в этих случаях также прибегают к стандартной процедуре расширения вектора состояний.
Так, если в уравнение состояния входит цветной шум x1
x·=f(x, u, t, x1)
и если можно выделить из него белый шум, например, операцией дифференцирования (это стандартный способ, называемый построением формирующего фильтра [140, 141]):
x·1=g(x1, t)+x2,
то, расширив пространство состояний, а именно приняв
xM={x, x1},fM={f, g},x={0, x2},
получим такую типовую формулу представления, но уже с белым шумом:
xM=M(xM, u, t)+x.
Класс аналитических моделей не ограничивается только моделями в частотной и временной областях. Известны статистические методы, которые не требуют наличия точной модели процесса [142]. В ряде случаев удается получить вполне удовлетворительные результаты. Так, например, сообщается, что, применяя корреляционные функции, можно обнаруживать сравнительно небольшие утечки жидкости
из трубопровода, локализуя место дефекта с точностью +0,7 % [143]. При длине трубопровода 70 км
с начальным давлением 69 атм. и расходом 330 м3/ч неисправность была обнаружена за 1,5 мин., при этом измерения с точностью 0,1 % фиксировали значения давления и расхода лишь на выходе и входе системы.
Представляют интерес методы диагностирования непосредственно по модели, заданной в виде дифференциальных уравнений. Переход в аварийное состояние связан со структурными изменениями модели. В работе [144] предлагается так называемый эволюционный подход, при котором диагностирование состояния системы проводится на основе вычисления функционала энергии и энтропии. Другие, более традиционные, подходы данного направления используют для качественного анализа динамической системы методы теории катастроф [145–147].
Теория катастроф позволяет определять закон управления, обеспечивающий оптимальное поведение объекта в точках бифуркации. Приложения методов этой теории к задаче алгоритмического обеспечения отказоустойчивости нелинейных объектов можно найти в статьях [148, 149].
Структурные методы анализа с помощью передаточных функций рассмотрены в работах [150–153]. По передаточным функциям отдельных компонент системы определяется [154] неисправное звено, причем осуществляется это методами, учитывающими погрешность идентификации модели, – методами сингулярного разложения матриц, интервального анализа, линейного программирования.
К аналитическим моделям относятся также модели, которые для диагностирования дефектов используют многочисленные методы теории идентификации, распознавания образов, теории чувствительности [2] и др.
Параметрическая диагностика на основе интервального анализа
Под параметрической диагностикой понимается «метод обнаружения и диагностики неполадок с помощью оценок переменных состояния и параметров модели» [13].
Общая схема параметрической диагностики может быть представлена [1, 155] следующим образом. Технологический процесс P характеризуется измеряемыми входными и выходными переменными X и ненаблюдаемыми переменными и параметрами Z, которые могут быть вычислены по математической модели процесса F. Переменные X – это значения температур, давлений, расходов, выходных концентраций, уровней, скоростей вращения роторов и т.п.; переменные Z характеризуют такие показатели, как коэффициенты полезного действия, скорости химических реакций, степени превращения вещества, содержание отдельных веществ в промежуточных и целевых продуктах.
На основании результатов измерений определяются малые отклонения X фактических значений от номинальных с точки зрения эффективности и безопасности ведения процесса, рассчитанных по математической модели F [156]. Отклонения ненаблюдаемых переменных Z определяются по математической модели A процесса P. По полученным данным оператор D осуществляет диагностирование и прогнозирование отказов процесса.
Обычно задача параметрической диагностики решается путем оперативного вычисления диагностических переменных через измеренные мгновенные значения косвенных технологических переменных, таких как температура, давление, расход и т.п. [157]. Однако в этом случае вычисленные параметры могут обладать очень большой погрешностью, поэтому система диагностики может часто выдавать сигналы ложной тревоги или пропускать дефекты. Это объясняется следующими факторами. Во-первых, мгновенные значения косвенных измеряемых переменных слишком чувствительны к шумовым помехам и могут случайным образом измениться на значительную величину. Во-вторых, измеряемые переменные относятся как к входу, так и к выходу объекта диагностики, поэтому их значения будут отличаться на величину запаздывания динамического канала между входом и выходом.
Основную идею применения интервального анализа для технической диагностики можно представить следующим образом [158]. Диагностический показатель представляется в виде интервала Y:
Y=[y_, y+] = {y|y_< y < y+; [y_, y+] Î R}, (2)
где y_, y+ – нижняя и верхняя границы интервала Y; y – число из интервала Y; R – множество вещественных чисел.
Интервальным расширением функции диагностического показателя f(y) со значениями в R называется интервальнозначная функция int вида
int[f(y)] = {min[f(y)], max[f(y)]}, (3)
где y Î W, W – ограниченная область в R.
Представляя малые отклонения технологических переменных ^X и ^Z в виде интервальных чисел, можно составить диагностическую модель в виде системы уравнений с интервальными коэффициентами и переменными [159]. Анализ полученных значений технологических переменных позволяет обнаруживать и прогнозировать дефекты объекта диагностики.
Метод параметрической диагностики, построенный на основе применения интервального анализа, позволяет снизить чувствительность к шумовым помехам [1]. Рассмотрим обоснование этого утверждения.
Пусть имеется функция плотности вероятности распределения случайной величины диагностируемого показателя для работоспособного fr(x) и дефектного fd(x) состояний непрерывного производства.
В виде гистограммы они показаны на рисунке 3.
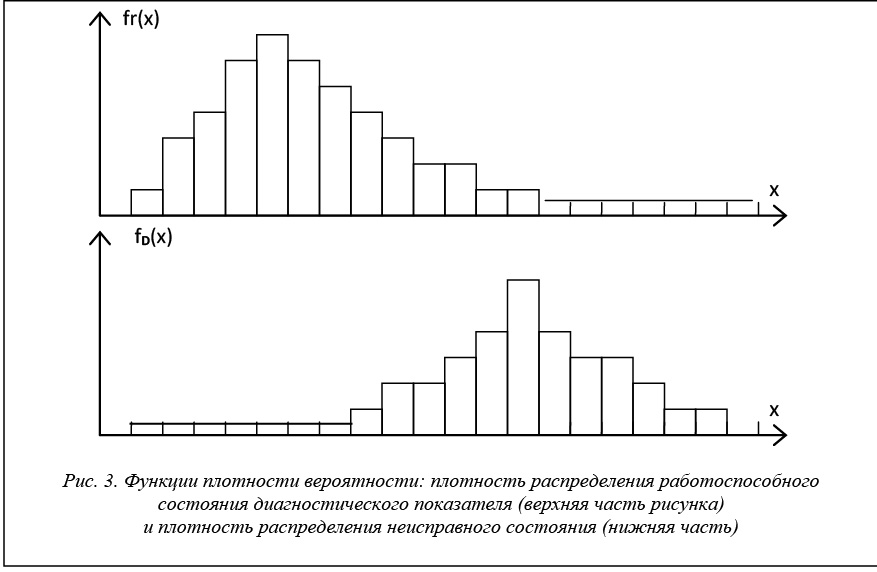
Для непрерывных производств обычно области работоспособного R и дефектного D состояний существенно пересекаются, поэтому принципиально невозможно избежать ошибочных решений [146]. Вероятность ложной тревоги и пропуска дефекта можно уменьшить, если анализировать не мгновенные значения диагностического показателя, а интервалы его изменения за заданный промежуток времени.
Пусть в течение времени T функционирования непрерывного производства значение диагностируемого показателя изменялось в диапазоне от x_ до x+. Для недопустимости ложной тревоги наиболее информативной является граница интервала x_. Пусть, например, в системе диагностики по мгновенному значению диагностического показателя используется именно это наилучшее значение показателя x_.
Тогда вероятность ложной тревоги системы диагностики по мгновенному значению диагностического показателя определится произведением двух вероятностей
Pмл = P1 , (4)
где Р1 – априорная вероятность работоспособного состояния R, которая определяется на основании предварительных статистических данных.
Вероятность (Pил) ложной тревоги системы диагностики по интервалу значений диагностического показателя
Pил = P1 , (5)
Из сравнения выражений (4) и (5) следует, что Pмл > Pил.
Вероятность пропуска дефекта системы диагностики непрерывного производства, построенного по принципу анализа мгновенного значения диагностического показателя, больше вероятности пропуска дефекта системы диагностики, построенной по принципу анализа интервала значений диагностического показателя [160].
Наиболее информативной с точки зрения предотвращения пропуска дефекта является граница x+ интервала диагностических показателей X. В этом случае вероятность пропуска дефекта по мгновенному значению
PМП = P2 , (6)
где P2 – априорная вероятность появления дефекта.
Вероятность пропуска дефекта по интервалу значений определится как
Pип = P2 , (7)
Из анализа (6) и (7) видно, что Pмп > Pип.
В настоящее время для химического производства одним из основных методов технической диагностики является метод параметрической диагностики, который имеет следующие особенности:
– при использовании параметрической диагностики возможен контроль ненаблюдаемых диагностических показателей путем их вычисления через наблюдаемые;
– параметрическая диагностика позволяет прогнозировать возникновение постепенных отказов; для этого необходимо анализировать процесс изменения во времени величины отклонения диагностических показателей от номинальных или граничных значений, отсюда следует, что характерной особенностью параметрической диагностики является выполнение диагностических операций не для абсолютных значений переменных, а для их отклонений;
– контроль диагностических показателей осуществляется большей частью не непрерывно, а дискретно, поэтому измеренный или вычисленный показатель характеризует объект диагностики на определенном интервале времени.
Проблемы диагностирования состояний и управления технологической безопасностью химических производств
Каждое химическое предприятие представляет собой совокупность непосредственно ХТС и системы автоматизированного управления, действующих как единое целое для получения заданного продукта или полупродукта.
ХТС находится под постоянным воздействием факторов внешней и внутренней среды. Внешняя среда оказывает воздействие через сырье, энергию, корректирующие установочные задания систем управления высших уровней и в некоторых случаях через климатические условия, в которых процессы осуществляют свою работу.
Внутренние факторы могут быть обусловлены либо ошибочными решениями персонала управления (технологов отделений, операторов) или обслуживающего персонала (аппаратчиков, слесарей), либо отказами технологического оборудования систем управления или технологическими отказами, которые обычно являются результатом неправильного ведения процесса.
Отказы оборудования, систем управления и технологии процессов можно разделить на две группы: постепенные (эффективностные) и внезапные.
Постепенные отказы связаны с постоянным ухудшением свойств оборудования систем управления и технологических условий ведения процесса. Все это объясняется тем, что оборудование ХТС в большинстве своем работает в условиях высоких температур, повышенных давлений, с агрессивными средами. Постоянно наблюдаются осаждение веществ на внутренней поверхности аппаратов и трубопроводов, коррозия материалов, что вызывает ухудшение их гидродинамических свойств и условий теплообмена, а также условий проведения массообменных и реакционных процессов.
Все это в конечном итоге приводит к необходимости останова технологического процесса на профилактическое обслуживание и ремонт либо может вызвать аварийную ситуацию, если упущен нужный момент для остановки технологического подразделения.
Большая доля аварийных ситуаций приходится на внезапные отказы, причинами возникновения которых являются как отступления от норм ведения технологического процесса, так и дефекты технологического оборудования или измерительных и управляющих цепей АСУ ТП.
Внезапные отказы могут быть разделены на постоянные отказы и сбои. Постоянный, или необратимый, отказ обычно требует остановки технологического процесса в отличие от сбоя, который чаще всего требует мелкого ремонта или незначительного изменения режима работы без остановки аппаратов на ремонт.
Нарушения, возникающие в технологических системах, носят стохастический характер, поэтому задача их раннего обнаружения и проведения профилактических мероприятий по их ликвидации является сложной и в настоящее время не имеет однозначного решения.
Для наиболее полной идентификации состояния ХТС необходимо на уровне информационно-управляющей системы технологических процессов организовать сбор и преобразование информации, характеризующей параметры внешней и внутренней среды. Это контроль параметров сырья, энергии, корректирующих управляющих воздействий, метеоусловий и т.п. (внешняя среда); контроль состояния оборудования, систем управления и параметров технологических процессов – ХТС.
Контроль состояния химико-технологических процессов должен включать в себя информационные каналы для анализа возможности возникновения постепенных и внезапных отказов оборудования систем управления и технологических процессов ХТС. В зависимости от возможностей комплекса технических средств, используемых на данном уровне информационно-управляющей системы, могут быть осуществлены классификация состояний ХТС и принятие решений о коррекции технологических режимов работы или проведении ремонтных работ с реализацией их либо через персонал обслуживания и управления, либо через исполнительную систему локальных контуров управления.
Каждая ХТС состоит из ряда элементов. Степень агрегирования элементов в основном определяется задачами управления. Число элементов ХТС конечно, и, следовательно, можно перечислить все возможные состояния, которые способны возникнуть в процессе ее работы.
Если число элементов ХТС равно N, число состояний для i-го элемента qi, то общее число состояний будет определяться по формуле
.
Таким образом, имеется конечное множество событий Е = {еi}, которые могут возникнуть в процессе функционирования системы, и U = {uj} – множество всех алгоритмов управления (команд), которые могут использоваться в системе. Введем отображение G:E®U множества событий на множество алгоритмов управления, такое, что если при появлении события ei необходимо применить алгоритм uj, то
G(ei) = uj. (8)
Если пара <er, uf> принадлежит отображению G, то отображение gr:{er}®{uf} будем называть алгоритмом принятия решения. В связи с этим об отображении G можно говорить как о множестве алгоритмов принятия решений. Обозначим символом P правило, задающее отображение G. Правило P определяется следующим образом: если для события еi и алгоритма управления uj выполняется (8), то
P(ei) = uj,
и наоборот.
Пусть D = {dh} (h = 1, ..., k) – некоторое вполне произвольное разбиение множества U. Введем на множестве E разбиение W = {wh}, каждый элемент которого определяется выражением
wh = {ei ½ G(ei) Î dh}, h = 1, ..., k, (9)
то есть wh – множество событий, которым соответствуют алгоритмы управления из множества dh. Элементы разбиения W назовем классами событий, а элементы разбиения D – классами алгоритмов управления. По аналогии с вышеизложенным определим разбиение V ={vh} множества алгоритмов принятия решений G, такое, что каждый элемент разбиения представляет собой отображение vh:eh®wh. При этом vh(ei)=uj, если G(ei)=uj, то есть отображение vh сохраняет свойство (9) отображения G, область определения отображения есть h-й класс событий, область значений - h-й класс алгоритмов управления. Элементы разбиения V назовем классами алгоритмов принятия решений.
Необходимость в классификации событий в технологических системах очевидна – она позволяет уменьшить количество переборов при выборе команд управления, то есть ограничить просмотр вариантов управляющих воздействий на систему только теми, которые соответствуют одному классу событий. Классификация событий позволяет выделить подграфы из графа событийной структуры и выделять наборы команд уже на основе подграфа отдельного класса событий.
Ядром современной системы управления технологической безопасности химического производства является система диагностики состояний ХТП.
Исследование проблемы диагностирования состояний и управления технологической безопасностью химических производств показало, что создание и использование диагностических систем для ХТП имеет ряд общих особенностей:
Стохастический и нечеткий характер технологических процессов, который приводит к тому, что не все состояния технологических установок являются наблюдаемыми или данные могут оказаться сильно зашумленными. При этом частым явлением оказывается выход из строя приборов, причем неисправности или дефекты элементов технологического оборудования, в которых протекают физико-химические процессы, находят свое отражение в переменных состояния ХТП.
В ХТП присутствуют нарушения разных типов: нарушения технологических режимов работы, нарушения в системах управления. Дефекты и неисправности технологического оборудования имеют качественно отличные первопричины возникновения, хотя в результате проявления этих нарушений мало чем отличаются между собой, в связи с этим возникают сложности определения первопричин возникшей ситуации.
Сложность определения первопричин приводит при создании систем диагностики к необходимости руководствоваться принципами:
– классификации состояний элементов;
– декомпозиции;
– иерархичности распознавания неисправностей и аварийных состояний;
– прогнозирования изменения состояний химического производства;
– управления критическими режимами.
Диагностика состояний и последующее принятие решений в зависимости от полноты информации о ХТС опирается на математический аппарат булевой, нечеткой, интервальной или вероятностной
логики.
Дискретный целочисленный характер структурных или организационно-технологических управляющих воздействий. Эта особенность учитывается как в математических моделях, так и в методах решения задач управления ХТП.
В настоящее время существует много различных подходов к решению проблемы определения состояний ХТП. Это модели булевой логики, нечеткой логики, байесовского подхода, причинно-следственные, пространства состояний, интервальные параметрические, дискретные модели.
Основные недостатки перечисленных выше подходов:
– Анализ состояний технологических режимов работы ХТП осуществляется на основе отдельных параметров или переменных состояния, которым присваивают название диагностических переменных. Сам анализ состояний осуществляется на основе ограничений, накладываемых на отдельные переменные состояния, при этом не всегда удается учесть их взаимосвязи. Между тем всегда существуют внешние возмущения, прикладываемые к объекту управления, которые приводят к одновременному изменению выходных переменных и к новым режимам работы. Отсюда следует сложность выявления первопричин появления того или иного состояния процесса и, как результат, возникновение неточностей и погрешностей диагноза. Этот недостаток относится в первую очередь к моделям пространства состояний и интервальным параметрическим моделям. В меньшей степени это относится к моделям булевой логики, нечеткой логики, байесовским и причинно-следственным моделям, так как в них заложена многоальтернативность определения первопричин.
– Модели булевой логики, нечеткой логики, байесовские модели при построении требуют обработки достаточно большого экспериментального материала и постоянной адаптации моделей в процессе работы ХТП в силу изменяющихся режимов работы и влияния случайных возмущений.
– Модели булевой логики, нечеткой логики, байесовские модели в основной своей массе являются аппроксимационными, вероятностными, оценочными и с формальных позиций не учитывают фундаментальных физико-химических законов протекания химико-технологических процессов;
– Прогнозирование на основе моделей состояний и интервальных параметрических моделей требует решения систем различных дифференциальных и алгебраических уравнений. Модели данного типа, позволяющие осуществлять диагностику состояний ХТС, построены на основе различных классов дифференциальных уравнений, обычно с учетом фундаментальных физико-химических законов (законов сохранения вещества и энергии), и их применение основано на использовании отличительных свойств решений для различных режимов работы технологических процессов. Однако их использование способно привести к большим временным издержкам, что может оказаться недопустимым при решении задач диагностики и управления технологической безопасностью.
– Во всех вышеперечисленных моделях диагностика состояний осуществляется на основе отдельных переменных или их некоторого множества, причем для конкретных состояний сами множества могут отличаться одно от другого. Само понимание состояния размыто и определяется конкретной технологической ситуацией, сложившейся в производстве, на основе эмпирической информации. Количество таких состояний не поддается строго формальной оценке и определяется в основном количеством производственных ситуаций, возникающих в процессе работы ХТС, эмпирическим путем. Такой подход требует большого объема работы, который необходимо выполнить на этапах исследования ХТС для того, чтобы классифицировать состояния технологии. При этом возникают сложности определения границ состояний ХТС, не говоря уже о том, что какие-либо изменения в ХТС могут потребовать дополнительных исследований новых различных технологических ситуаций.
Особенностью задачи диагностики состояний ХТП является нечеткий характер критериев выбора альтернатив поиска дефектов или нарушений, возникающих в процессе функционирования ХТП, их параметров, ограничений и т.д. Вследствие этого во многих случаях оказывается невозможным построение адекватной математической модели исследуемой проблемы, что влечет за собой необходимость использования экспертных оценок, которые часто оказываются единственной информацией для принятия решений. Естественно, возникает необходимость разработки методов, позволяющих эффективно получать и обрабатывать нечеткую экспертную информацию. Лучше всего данным требованиям удовлетворяет класс дискретных моделей, позволяющий проводить анализ состояния работоспособности системы в условиях неопределенности информации о диагностируемом объекте.
Перечислим основные свойства, характеризующие дискретные модели:
– дают четкую дифференциацию состояний системы;
– позволяют учесть не только изменения технологических режимов работы, но и изменения состояния аппаратов и систем управления ХТП;
– обладают большим быстродействием по сравнению с моделями, построенными на основе дифференциальных или алгебраических уравнений.
Кроме того, уже на этапах построения дискретных моделей можно решать задачу координации работы отдельных аппаратов ХТС, судить о том, какой должна быть система контроля, и закладывать основы диагностики состояний ХТС и построения информационно-управляющей системы.
Основной проблемой промышленных систем диагностики является своевременное обнаружение нарушений, которые приводят к внештатным ситуациям. В этой связи актуальными являются задача поиска первичной неисправности и задача анализа возможного негативного влияния этой неисправности на следующие по цепочке узлы и аппараты.
В качестве математического аппарата для построения качественной картины развития опасностей
в данной работе предлагается использовать нечеткие бинарные отношения, позволяющие подойти
к вопросу создания цепочек взаимовлияний опасностей с более формальных позиций и расширить множество поиска возможных вариантов развития опасностей. Кроме того, данный метод должен использовать экспертные оценки.
Результатом этого анализа должна стать оценка возможного уровня опасности. В данной работе предлагается количественно оценивать уровень опасности как степень удаленности текущего состояния процесса от области центра безопасности, в котором функционирование процесса является наиболее безопасным.
Литература
- Палюх Б.В. Основы построения и разработки автоматизированной системы управления эксплуатационной надежностью химических производств: дис. … докт. техн. наук (05.13.06). М., 1991. 360 с.
- Воронин В.В., Воронин В.В., Констанди Г.Г., Январев Ю.Э. Диагностирование динамических объектов непрерывного типа. Л.: ЦНИИ Румб, 1986. 137 с.
- Карибский В.В., Пархоменко П.П., Согмонян Е.С., Халчев В.Ф. Основы технической диагностики. Модели объекта, методы и алгоритмы диагноза. М.: Энергия, 1976. 496 с.
- Пархоменко П.П., Согомонян Е.С. Основы технической диагностики. Оптимизация алгоритмов диагностирования, аппаратурные средства. М.: Энергоатомиздат, 1981. 320с.
- Технические средства диагностирования: справочник; [под ред. В.В. Клюева]. М.: Машиностроение, 1989. 672 с.
- Гольдман Р.С Логические модели диагноза непрерывных объектов // Автомат. и телемех. 1979. № 5. С. 149–156.
- Шаршумов С.Г. Особенности диагноза технического состояния многовыходных объектов с использованием таблиц неисправностей // Автомат. и телемех. 1973. № 12. С. 161–168.
- Чикулис В.П. Методы минимизации разрешающей способности диагноза и диагностической информации // Автомат. и телемех. 1975. № 3. С. 133–141.
- Гарковенко С.Н., Сагунов В.И. О доопределении минимальной совокупности точек контроля с целью поиска неисправности произвольной кратности в непрерывных объектах диагностирования // Автомат. и телемех. 1977. № 7. С. 175–179.
- Kramer M.A. IFAC Workshop: Fault detection andsafety in chemical plants, Kyoto, 1986.
- Pattipati K.R., Alexandridis M.G. IEEE Trans.Syst. Man Cybern. 1990, vol. 20, no. 4, pp. 872–887.
- Berenblut B.J., Whitehouse H.B. Chem. Eng., 1977, vol. 318, pp. 175–181.
- Химмельблау Д. Обнаружение и диагностика неполадок в химических и нефтехимических процессах. Л.: Химия, 1983. 352 с.
- Salem S.L., Apostolakis G.e., Okrent D. // Annalis of Nucl. Energy, 1977, 4, pp. 417–433.
- Salem S.L., Wu J.S., Apostolakis G.e. Nucl. Technol., 1979, vol. 42, pp. 51–64.
- Worrel R.B. IEEE Trans. Reliab., 1981, R-30, no. 2, pp. 98–100.
- Pollack S.L. Decision Table: Theory and Practice. NY: Wiley Intersience, 1971, 275 p.
- Хенли Э. Дж., Кумамото Х. Надежность технических систем и оценка риска. М.: Машиностроение, 1984. 528 с.
- Гуляев В.А., Бугаев А.Е. Логико-лингвистические методы в задачах диагностирования сложных объектов. Киев: Ин-т пробл. моделир. в энерг. 1989. Вып. 20. 28 с.
- Kramer M.A. AIChE J, 1987, vol. 33, no. 1. pp. 130–140.
- Кафаров В.В., Дорохов И.Н., Марков Е.П.. Системный анализ процессов химической технологии. Применение метода нечетких множеств. М.: Наука, 1986. 360 с.
- Tong R.M. // Automatica, 1977, vol. 13, no. 6, pp. 559–569.
- Umeda T., Kuryama T., O'Shima E.O., Matsuyama H. Chem. Eng. Sci, 1980, no. 35, pp. 2379–2384.
- Tsuge Y., Shiozaki J., O'Shima E., Matsuyama H. I. Chem. Eng. Symp. Ser., 1985, vol. 92, pp. 133–144.
- Shiozaki J., Shibata B.,O'Shima E., Matsuyama H. Proc. Int. Workshop Artif. Intell. Ind. Appl., HitachiCity, 1988, pp. 461–466.
- Kokawa M., Miyazaki S., Shingai S. Automatica, 1983, no. 19, pp. 729–738.
- Plamping K., Andow P.K. Trans. Inst. Contr., 1983, 5, no. 3, pp. 161–166.
- Iri M., Aoki K., O'Shima E., Matsuyama H. Comp. Chem. Eng. 1979, no. 3, pp. 489–495.
- Shiozaki J., O'Shima E., Matsuyama H., Iri M. Comp. Chem. Eng. 1985, vol. 9, no. 3, pp. 285–293.
- Kramer M.A., Palowitch J. AIChE J. 1987, vol. 33, no. 7, pp. 1067–1078.
- Sun S.S., Hsu J.P. J. Chin. Inst. Chem. Eng. 1989, vol. 20, no. 2, pp. 109–112.
- Moore R.L., Kramer M.A. Expert Systems in OnLine Process Control. Chem. Proc. Control 3, Asimodar, 1986.
- Davis R. Diagnostic reasoning Based on Structureand Behavior. Qualitative Reasoning About Physical Systems. Amsterdam: Elsevier, 1984.
- Rasmussen J. IEEE Trans. Systems, Man, Cybern. 1985, SMC, vol. 15, no. 2, pp. 234–243.
- Shafaghi A.P., Andow P.K., Lees F.P. Chem.Eng. Des. 1984, vol. 62, pp. 101–111.
- Finch F.E., Kramer M.A. AChI J., 1988, vol. 34, no. 1, pp. 25–36.
- Горелов О.И. Поиск дефектов в сложных технических системах методами анализа диагностических графов. Вычисление дефектных компонент и межкомпонентных связей // Автомат. и телемех. 1989. № 9. С. 148–159.
- Nageswara Rao S.V., Viswanadham N. Int. J.Syst. Sci., 1987, vol. 18, no. 4, pp. 687–695.
- Shiozaki J., Matsuyama H. Sel. Papers 5th IFACSymp., Tokyo, 1986, pp. 373–378.
- Hura G.S., Atwood J.W. IEEE Trans. Reliab., 1988, vol. 37, no. 5, pp. 469–474.
- Леман Э. Проверка статистических гипотез. М.: Наука, 1984. 418 с.
- Ammar H., Huang Y.F., Liu R.W. Proc. Int.Symp. Circuit a. Syst. Kyoto, 1985, no. 2, pp. 743–746.
- Kerpelman D.I. Proc. IEEE Int. Symp. Intell.Contr., Arlington, 1988, pp. 703–708.
- Zargham M.R., Danhof K.J. Int. Process Lett. 1990, 34, no. 6, pp. 299–305.
- Бестужева И.И., Руднев В.В. Временные сети Петри. Классификация и сравнительный анализ // Автомат. и телемех. 1990. № 10. С. 3–21.
- Watanabe K., Matsuura I., Abe M., Kubota M. AIChE J. 1989, vol. 35, no. 1, pp. 1803–1812.
- Venkatasubramanian V., King Chan. AIChE J. 1989, vol. 35, no. 12, pp. 1993–2002.
- Shaw W.T. Adv. Instrum. and Contr. Proc. ISAInt. Conf. and Exhib., Philadelphia, 1989, vol. 44, no. 2, pp. 465–478.
- Hoskins J., Himmelblau D. Europ. Symp. Contr.Appl. Chem. Ind., Erangen. 1989, 561–572.
- Venkatasubramanian V., Vaidyanathan R., Yamamoto Y. Comput. Chem. Eng. 1990, vol. 14, no. 7, pp. 699–712.
- Guarro S.B. Reliab. Eng. Syst. Saf. 1990, vol. 30, no. 1/3, pp. 21–50.
- Guarro S.B., Okrent D. Nucl. Techn. 1984, vol. 67, pp. 348–359.
- Guarro S.B. Reliab. Eng. Syst. Saf. 1988, vol. 22, pp. 313–332.
- Kumamoto H., Henley E.J., Inoue K. IEEEtrans. Reliab. 1981, R30, pp. 110–115.
- Lind M. Human Detection and Diagnosis of System Failures. NY: Plenum Press, 1981, pp. 411–419.
- US. Atomik Energy Commission, Reactor Safety Study. An assessment of accident riscs in US commerical nuclear power plants. Rep. WASH1400. Washington, 1975, 311 p.
- Reliability and fault tree analysis: Theoretical and applied system reliability and safety assessment. Ed. by Barlow R.E., Fussel J.B., Singpurvala N.D. Philadelfia: SIAM, 1975, 972 p.
- Accident Sequence Medeling: Human Action, System Response, Intelligent Decision Support. Reliability.Eng. Syst. Saf. 1988, 22, no. 14. pp. 14–72.
- Lee W., Grosh D.L., Tillman F.A., Lie C.H. IEEE Trans. Reliab. 1985, R34, no. 3, pp. 194–203.
- Chunning Y. Microelectron. Reliab. 1990, vol. 30, no. 5, pp. 891–895.
- Lees F.P., Andow P.K., Murphy C.P. Reliab.Eng. 1980, no. 1, pp. 149–156.
- Andow P.K. IEEE Trans. Reliab. 1980, R29, pp. 2–9.
- Andow P.K. Microelectron. Reliab. 1983, vol. 23, no. 2, pp. 325–328.
- Bechta D.J. IEEE Trans. Reliab. 1989, vol. 38, no. 2, pp. 177–185.
- Kafrawy K., Rushdi A.M. Microelectron. Reliab. 1990, vol. 30, no. 1, pp. 157–175.
- Kai Y. Reliab. Eng. Syst. Saf. 1990, vol. 28, no. 1, pp. 1–7.
- Schneeweiss W.G. IEEE Trans. Reliab. 1990, 39, no. 3, pp. 296–300.
- Lambert N.E. Chem. Eng. Progr. 1977, vol. 73, pp. 82–85.
- Lambert N.E. IEEE Trans. Reliab. 1983, R32, no. 5, pp. 422–425.
- Salter B.B., Goodwin E.F. Proc. 8th Trien.IFAC World Congr., Kyoto, 1981, no. 3, pp. 1799–1904.
- Hessian R.T., Salter B.B., Goodwin E.F. IEEETrans. Reliab. 1990, vol. 39, no. 1, pp. 87–91.
- Fussel J.B. Nucl. Eng. Des. 1973, vol. 52, pp. 337–360.
- MartinSolis G.A., Andow P.K., Lees F.P. LossPrevention and Safety Promotion in the Process Industries. Frankfurt: DECHEMA, 1977, no. 2, pp. 367–385.
- MartinSolis G.A., Andow P.K., Lees F.P. LossPrevention and Safety Promotion in the Process Industries. Basel: Swiss Soc. Chem. Ind., 1980, no. 3, pp. 554–556.
- MartinSolis G.A., Andow P.K., Lees F.P. Trans. I. Chem. Eng. 1982, vol. 60, pp. 14–20.
- Andow P.K., Lees F.P. Trans. I. Chem. Eng. 1975, vol. 54, pp. 195–199.
- Andow P.K. Comput. Chem. Eng. 1980, no. 4, pp. 143–153.
- Salem S.L., Apostolakis G.e., Okrent D. Trans. Amer. Nucl. Soc. 1975, 22, pp. 475–485.
- Salem S.L., Apostolakis G.E. Synthesis and Analysis Methods for Safety and Reliability Studies. NY: Plenum press, 1978, pp. 109–112.
- Taylor J.R. Reliability and Fault tree Analisis. Philadelphia: SIAM, 1975, pp. 881–894.
- Производство азотной кислоты в агрегатах большой единичной мощности; [под ред. В.М. Олевского]. М.: Химия, 1985. 400 с.
- Neilsen D. Ibid. pp. 849–894.
- Taylor J.R., Hollo E. Nucl. Syst. Reliab.Eng. and Risk Assessment, SIAM, 1977.
- Camarda P.,Corsi F. IEEE Trans. Reliab. 1978, R-27, pp. 215–221.
- Aggarwal K.K. IEEE Trans. Reliab. 1979, R-28, p. 309.
- Han S.H., Kim T.W., Choi Y., Yoo K.J. Reliab.Eng. Syst. Saf. 1989, vol. 25, no. 1, pp. 15–31.
- Kumamoto H., Henley E.J. Ind. Eng. Chem.Fundam. 1986, vol. 25, pp. 233–239.
- Taylor J.R. IEEE Trans. Reliab. 1982, R-31, pp. 137–143.
- Powers G.J., Tompkings F.C. AIChE J. 1974, vol. 20, no. 2, pp. 376–384.
- Powers G.J., Lapp S.A. Chem. Eng. Prog. 1976, vol. 72, no. 4, pp. 89–93.
- Powers G.J., Lapp S.A. IEEE Trans. Reliab. 1977, R-26, pp. 2–13.
- Lapp S.A., Power G.J. Ibid. 1979, R-28, pp. 12–14.
- Henley E.J., Kumamoto H. Ibid. 1977, R-26, pp. 316–317.
- Locks M.O. Ibid. 1979, R-28, pp. 2–5.
- Lambert H.E. Ibid., pp. 6–9.
- Yellman T.W. Ibid., pp. 10–11.
- Andrews J.D., Morgan J.M. Reliab. Eng. 1986, vol. 14, no. 2, pp. 85–106.
- Kohda T., Henley E.J. Reliab. Eng. Syst.Saf. 1988, vol. 20, no. 1, pp. 35–61.
- Ulerich N.H., Powers G.J. IEEE Trans. Reliab. 1988, vol. 37, no. 2, pp. 171–177.
- Andrews J., Breunan G. Reliability'89, Proc.Birmingam, 1989, no. 2, pp. 4C(4) 1–28.
- DE Vries R.C. IEEE Trans. Reliab. 1990, vol. 39, no. 1, pp. 76–86.
- Andrews J., Breunan G. Reliab. Eng. Syst.Saf. 1990, vol. 28, no. 3, pp. 357–384.
- Mullhi J.S., Ang M.L., Lees F.P., Andrews J.D. Reliab. Eng. 1986, vol. 16, no. 1, pp. 3–108.
- Mullhi J.S., Ang M.L., Lees F.P., Andrews J.D. Ibid. 1988, vol. 23, no. 1, pp. 21–51.
- Galluzo M., Andow P.K. Reliab. Eng. 1984, no. 7, pp. 193–211.
- Kumamoto H., Henley E.J., Inoue K. IEEEtrans. Reliab. 1981, R30, pp. 110–115.
- Andow P.K. Trans. Inst. Chem. Eng. 1981, vol. 59, pp. 125–128.
- Kumamoto H., Henley E.J. AIChE J. 1979, vol. 25, pp. 108–113.
- Amandola A. Reliab. Eng. Syst. Saf. 1988, vol. 22, pp. 3–25.
- Aldermir T. IEEE Trans. Reliab. 1987, R-36, pp. 133–144.
- Caccibue P.C., Amendola A. Nucl.Technol. 1986, vol. 74, pp. 196–208.
- Ливанов Ю.В. // Изд. АН СССР. Сер. Техн. киберн. 1990. № 6. С. 178–184.
- Knowlton R.E. An Introduction to Hazar and Operabiliuty Studies. Vancouver: Chemetics Int. Company, 1987, 328 p.
- Lawley H.G. Chem. Eng. Progr. 1974, vol. 70, no. 4, pp. 45–56.
- ГОСТ 27.00289. Надежность в технике. Основные понятия. Термины и определения. М.: Изд-во стандартов, 1989. 37 с.
- Guidelines for Hazard Evaluation Procedures. AChI, Center for Chem. Process Safety. NY, 1985, 128 p.
- Guidelines for Chem. Process Quantitative RiskAnalisys. AChI, Center for Chem. Process Safety. NY, 1989, 111 p.
- Garmody T.W. Reliab. Eng. Syst. Saf. 1990, vol. 29, no. 1, pp. 5–14.
- Elliot D.M., Owen J.M. Chem. Eng. 1968, vol. 223, CE 377.
- Lawley H.G. Loss Prevention. New York: AIChE, 1974, vol. 8, pp. 105–109.
- Gibson S.B. Chem. Eng. 1976, vol. 306, pp. 105–109.
- Chemical Industries Associatin. Hazard and Operability Studies. London: Chem. Ind. Assn., 1977, 98 p.
- Knowlton R.E. Hazop and its contribution toplant operability. Design 79. Inst. Chem. Eng., Rugby, 1979, pp. 130–132.
- Lihou D. Safety Promotion and Loss Preventionin Process Industries. London: Oyez, 1980, 78 p.
- Lihou D., Rahimi R., Fletcher J.P. Loss Prevention and Safety Promotion in Process Industries. Basel: Swiss Soc. Chem. Ind., 1980, no. 3, pp. 579–582.
- Taylor J.R. CSNI Meeting Develop. Appl. Reliab. Thechn. to Nucl. Plants, Liverpool. 1974, pp. 612–615.
- Дубравский Н.Г., Мокроус М.Ф. Параметрические методы диагностического контроля состояния авиадвигателей // Труды ЦИАМ. 1981. № 964. 29 с.
- Lees F.P. Comput. Chem. Eng. 1984, vol. 8, no. 2, pp. 91–103.
- Rakic P., Pavlovic Z. Proc7 7th Symp.Reliab.Electron., Budapest, 1988, no. 1, pp. 339–346.
- Willems J.C. Ric. Aut. 1979, no. 10, pp. 71–106.
- Виллемс Я.К. Теория систем. Математические методы и моделирование: сб. статей. Сер. Математика. Новое в зарубежной науке. Вып. 44; [пер. с англ.]. М.: Мир, 1989. С. 81–91.
- Ван дер Шафт А. Теория систем. Математические методы и моделирование: сб. статей. Сер. Математика. Новое в зарубежной науке. Вып. 44; [пер. с англ.]. С. 192–237.
- Getler J. IEEE Contr. Syst. Mag. 1988, vol. 8, no. 6, pp. 3–11.
- Ricker L. Ind. Eng. Chem. Res. 1990, vol. 29, pp. 374–392.
- Watanabe K., Himmelblau D. Int. J. Syst.Sci. 1982, vol. 13, no. 2, pp. 137–158.
- Willsky A.S. Automatica. 1976, vol. 12, no. 6, pp. 601–611.
- Isermann R. Automatica. 1984, vol. 20, no. 4. pp. 384–404.
- Венгеров А.А., Щаренский В.А. Прикладные вопросы оптимальной линейной фильтрации. М.: Энергоатомиздат, 1982. 192 с.
- Справочник по теории автоматического управления; [под ред. А.А. Красовского]. М.: Наука. Гл. ред. Физматлит, 1987. 712 с.
- Доценко Б.И. Диагностирование динамических систем. Киев: Техника, 1983. 159 с.
- Siebert H., Klaiber T. Process Aut. 1980, no. 1, pp. 91–96.
- Stafanov S.Z. Int. J. Syst. Sci. 1989. 26, no. 5, pp. 865–888.
- Арнольд В.И. Теория катастроф. М.: Наука, 1990. 128 с.
- Биргер И.А. Техническая диагностика. М.: Высш. школа, 1978. 240 с.
- Постон Т., Стюарт М. Теория катастроф и ее приложения. М.: Мир, 1980. 608 с.
- Томпсон Дж. Неустойчивости и катастрофы в науке и в технике. М.: Мир, 1985. 256 с.
- Kasumasa H., Masataka I., Toshimitnu U. IEEETrans. Auto. Contr. 1981, AC-26, no. 2, pp. 601–603.
- Casti J. IEEE Trans. Auto. Contr. 1980, AC2-5, no. 5, pp. 1008–1011.
- Park S.W., Himmelblau D.M. Comput. Chem. Eng. 1987, vol. 11, no. 6, pp. 713–722.
- Корноушенко Е.К., Пылаев Н.К. Передаточные числа и диагностирование линейных систем // Докл. АН СССР. 1988, vol. 300, no. 3, pp. 559–561.
- Новый подход к диагностированию линейных диагоностических систем // Автомат. и телемех. 1989. № 5. С. 148–159.
- Герасимов В.В., Корноушенко Е.К. Диагностирование динамических систем, заданных структурными схемами с нелинейными и нестационарными элементами // Автомат. и телемех. 1990. № 4. С. 133–144.
- Парамонова Г.Г. Обнаружение неисправных звеньев в линейных системах с учетом погрешности идентификации // Автомат. и телемех. № 2. С. 152–160.
- Черкез А.Я. Инженерные расчеты газотурбинных двигателей методом малых отклонений. М.: Машиностроение, 1965. 355 с.
- Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений. М.: Наука, 1970. 104 с.
- Алефельд Г., Херцбергер Ю. Введение в интервальные вычисления. М.: Мир, 1987. 360 с.
- Куперман В.Г. Разработка гибридных автоматизированных систем технической диагностики непрерывных химических производств (на примере производства азотной кислоты). Автореф. дис. … канд. техн. наук. М., 1991. 16 с.
- Калмыков С.А., Шокин Ю.И., Юлдашев З.Х. Методы интервального анализа. Новосибирск: Наука, 1986. 224 с.
- Кафаров В.В., Палюх Б.В., Перов В.Л. Решение задачи технической диагностики непрерывного производства с помощью интервального анализа // Докл. АН СССР. 1990. Т. 311. № 3. C. 677–680.
MATHEMATICAL MODELS USED IN THE DIAGNOSTICS OF TECHNOLOGICAL SYSTEMS
Vent D.P., Dr. Sc. (Engineering), Professor; Prorokov A.E., Ph.D. (Engineering), Associate Professor; Sanaeva G.N., Senior Lecturer
(Novomoskovsk Institute of MUCTR. D.I. Mendeleev, Druzhby st. 8, Tula Reg., Novomoskovsk,
301665, Russian Federation, k_vtit@dialog.nirhtu.ru);
Toichkin N.A., Ph.D. (Engineering), Associate Professor, toichkin@list.ru
(Kola branch of Petrozavodsk state University, Lesnaya st. 29, Murmansk Reg., Apatity,
184209, Russian Federation);
Palyukh B.V., Dr.Sc. (Engineering), Professor; Semenov N.A., Dr.Sc. (Engineering), Professor;
Bogatikov V.N., Dr.Sc. (Engineering), Professor; Alekseev V.V., Ph.D. (Engineering), Associate Professor; Kemaykin V.K., Ph.D. (Engineering), Associate Professor
(Tver State Technical University, Nikitin Quay 22, Tver, 170026, Russian Federation, is@tstu.tver.ru)
Abstract. The paper deals with mathematical models used in the diagnostics of the technological system states: structural – logical model; causal model; state space model; interval parametric models. The problems of diagnostics states and control of technological safety of chemical production are discussed.
It is shown that the core of modern management system of technological safety of chemical production, is a diagnostic system of chemical-technological process states and are some common features of the establishment and use of diagnostic systems for chemical-technological process.
The conclusion about the need to build diagnostic systems based on chemical-technological process class of discrete models, which allow the analysis of the system availability under uncertainty information about diagnosed object.
Keywords: technological safety, mathematical model, security control, object control, chemical-technological process, discrete models, state of the process, chemical-technological system, system availability.
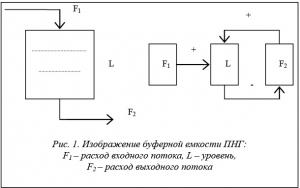
Комментарии