Оптимизация системы технического обслуживания и ремонта (ТОР) направлена на уменьшение эксплуатационных затрат предприятий.

Большинство существующих современных моделей оптимизации ТОР основаны на использовании функции распределения 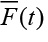 наработки на отказ. Классическая модель описана в работе [1].

Интенсивность эксплуатационных затрат R(t) рассчитывается по формуле

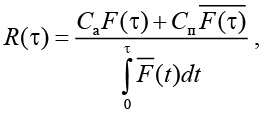
где Сa – средние затраты на аварийное восстановление; Cп – средние затраты на профилактическое восстановление; t – период проведения профилактических работ; F(t) – функции распределения наработки до отказа.

При этом tопт. является решением уравнения 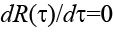 или

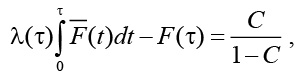
где С=Сп /Са, l(t) – функция интенсивности отказов.

Для определения функции распределения  проводят испытания оборудования на надежность или сбор и обработку информации об отказах в процессе его эксплуатации. Это требует материальных затрат. В первом случае они зависят от стоимости испытательных стендов, образцов и времени проведения испытаний, во втором случае в большей степени от времени проведения наблюдений за отказами оборудования. Сокращение времени испытаний или наблюдений в процессе эксплуатации позволяет снизить затраты на определение показателей надежности, но при этом возникают цензурированные выборки наработок на отказ.

Расчет показателей надежности по цензурированным выборкам выполняется методом максимального правдоподобия [2]. Уменьшение времени испытания оборудования на надежность или наблюдения за отказами в процессе его эксплуатации должно быть обосновано исследованиями достоверности метода максимального правдоподобия.

В статье представлены экспериментальные исследования оценок максимального правдоподобия экспоненциального закона распределения по малым, многократно цензурированным справа выборкам.
Такие выборки возникают при проведении наблюдений за отказами в процессе эксплуатации или при проведении испытаний по плану [N, M, T], который приведен в [3]. Это план испытаний, согласно которому одновременно испытывают N объектов, после каждого отказа объект восстанавливают, каждый объект испытывают до истечения времени испытаний или наработки T.

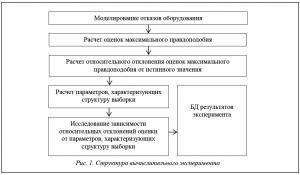
Для выполнения исследований разработаны алгоритмы и написана программа на языке Fox Pro, позволяющая выполнять имитационное моделирование отказов оборудования, возникающих в процессе эксплуатации, и провести вычислительный эксперимент по исследованию точности оценок максимального правдоподобия. Структура вычислительного эксперимента приведена на рисунке 1.

Моделирование на ЭВМ многократно цензурированных справа выборок случайных величин, распределенных по экспоненциальному закону, выполняется по следующему алгоритму.

1. Генерируется случайная величина t, распределенная по исследуемому экспоненциальному закону распределения, рассчитываемая по формуле

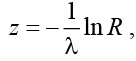
где R –  случайная величина, равномерно распределенная на интервале (0,1) [4].

2. Генерируется случайная величина t, распределенная по цензурирующему закону распределения.
В качестве цензурирующего закона применялся усеченный справа нормальный закон распределения.

3. Сравниваются полученные случайные величины. Если t < t, к моделируемой выборке добавляется случайная величина t, соответствующая наработке до отказа. Если t > t, к моделируемой выборке добавляется случайная величина t, соответствующая наработке до цензурирования.

4. Процесс моделирования продолжается до тех пор, пока число полученных случайных величин не станет равным заданному числу членов выборки N (объему выборки).

На ЭВМ моделировались многократно цензурированные справа выборки случайных величин объемом N=5, 10, 15, 20, 25.  Генерирование выборок выполнялось при следующих ограничениях:

5 £ N < 10, q ³ 0,5;

10 £ N < 20, q ³ 0,3;

20 £ N £ 50, q ³ 0,2,

где q – степень цензурирования выборки. 

Количество сформированных выборок V для каждого значения N равно 3 000. По каждой выборке методом максимального правдоподобия рассчитывались оценки экспоненциального распределения и их относительные отклонения d от истинных значений по формуле

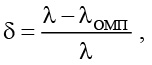
где λ – истинное значение параметра экспоненциального распределения; λомп – оценка максимального правдоподобия экспоненциального распределения.

В исследованиях ставилась задача получения универсальных уравнений, которые можно применять для оборудования с разными значениями средних наработок до отказа. Поэтому параметр λ исследуемого закона распределения рассчитывался для каждой генерируемой выборки с использованием случайного числа, равномерно распределенного на интервале [0,1] по формуле

λ = 0.6 + 0.4*RAND()

где RAND() – функция генерации случайного числа, равномерно распределенного на интервале [0,1], языка программирования Fox Pro.

Чтобы избежать повторения последовательностей псевдослучайных чисел, перед формированием каждой выборки генерировалось случайное число на основе системного времени. Для этого использовалась функция RAND() с отрицательным аргументом – RAND(-1). Получение достаточной разницы в системном времени при генерации выборок осуществлялось с помощью задержки времени до 30 миллисекунд перед каждым циклом формирования однократно цензурированной выборки.

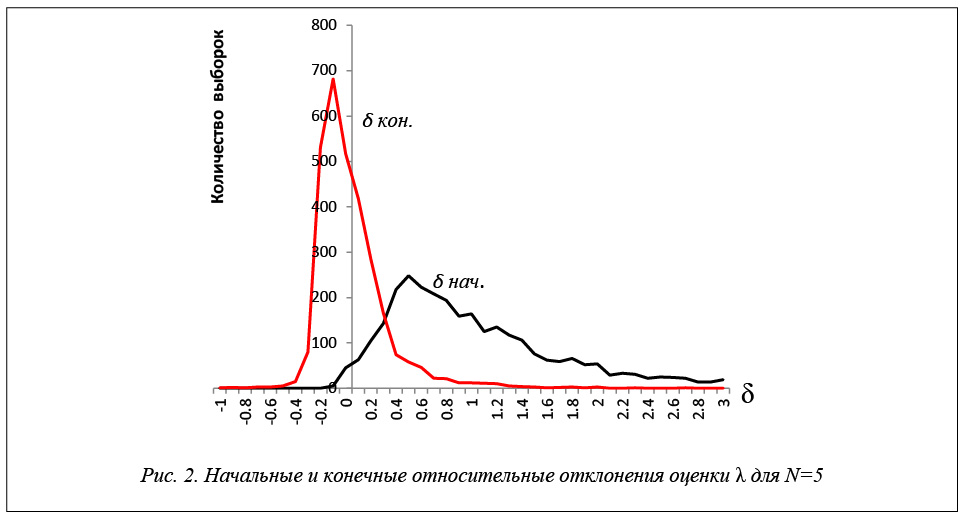
По  результатам моделирования построены гистограммы относительных отклонений оценок максимального правдоподобия экспоненциального распределения. По оси ординат отложен процент оценок от общего количества, попавших в данный интервал. Полученные результаты приведены на рисунке 2.

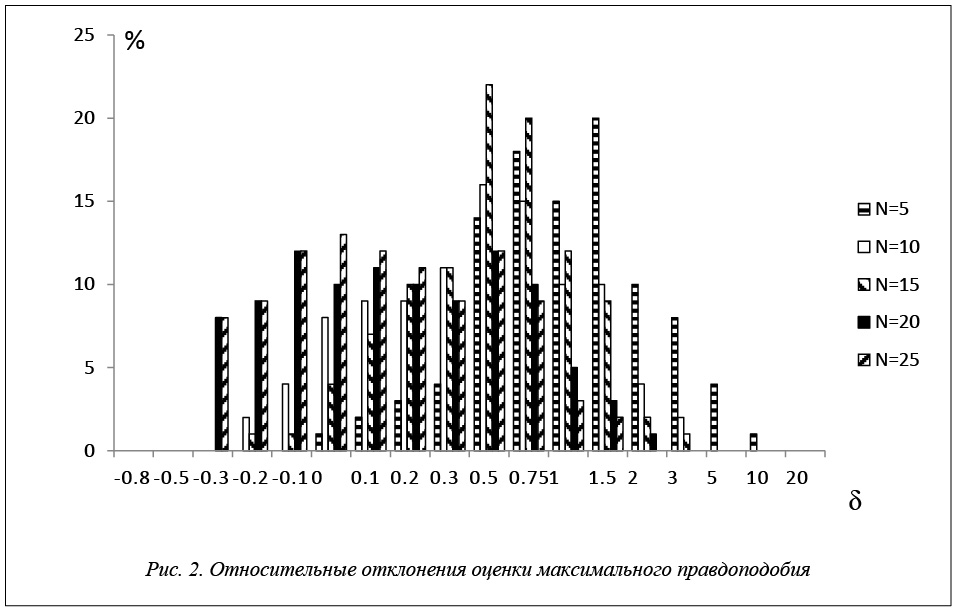
Эти экспериментальные данные показывают, что большинство оценок максимального правдоподобия экспоненциального распределения, полученные по малым, многократно цензурированным справа выборкам, имеют значительные отклонения от истинных значений. Например, 1 % оценок при N=5 имеют относительные отклонения от 10 до 20; 4 % – от 5 до 10; 8 % – от 3 до 5. При увеличении объема выборки N точность оценок возрастает. При N=25 относительные отклонения оценок экспоненциального закона распределения не превышают 2. Несмотря на это, 2 % оценок имеют относительные отклонения от 1,5 до 2; 3 % – от 1 до 1,5; 9 % – от 0,75 до 1; 12 % – от 0,5 до 0,75. При N=5, 10, 15 отчетливо видно сильное смещение оценок максимального правдоподобия.

В целом можно сделать вывод, что точность метода максимального правдоподобия при значениях
N < 25 низка. Относительное отклонение оценок от истинных значений может достигать 3 и более, а половина всех оценок имеет отклонения больше 0,3 в зависимости от объема выборки.

В работах [5, 6] предложена методика повышения точности оценок максимального правдоподобия при проведении испытаний по плану [N, U, T].

В данной статье разработаны модели повышения точности оценок максимального правдоподобия по малым, многократно цензурированным выборкам, формирующимся при проведении наблюдений за отказами в процессе эксплуатации или при проведении испытаний по плану [N, M, T].

Для построения моделей для каждой сгенерированной выборки выполнен расчет параметров выборки, характеризующих ее структуру. Для описания структуры сформированной выборки случайных величин в работе использовались пять стандартных параметров выборки:

X1 – степень цензурирования;

X2 – коэффициент вариации;

X3 – коэффициент вариации полных случайных величин;

X4 – эмпирический коэффициент асимметрии;

X5 – коэффициент эксцесса.

Еще пять параметров представляют собой математические выражения, составленные из стандартных характеристик выборки:

X6 – отношение математического ожидания полных случайных величин к математическому ожиданию всех членов выборки;

X7 – отношение математического ожидания цензурированных случайных величин к математическому ожиданию всех членов выборки;

X8 – относительное отклонение математического ожидания от середины вариационного размаха;

X9 – отношение медианы к математическому ожиданию;

X10 – отношение моды к математическому ожиданию.

Все параметры измеряются в относительных единицах и не зависят от абсолютных значений случайных величин. Это сделано для того, чтобы можно было применять полученные уравнения к оборудованию со средними наработками на отказ разной величины.

В результате исследований построены регрессионные математические модели, устанавливающие связь между относительным отклонением оценки МП от истинного значения и параметрами, характеризующими структуру выборки. Для каждого объема выборки N построено свое уравнение регрессии.

Математические модели построены в классе линейных уравнений регрессии вида

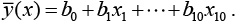                                                      (1)

Коэффициенты b0, b1, …, b10 и параметры значимости уравнений регрессии приведены в таблице 1.

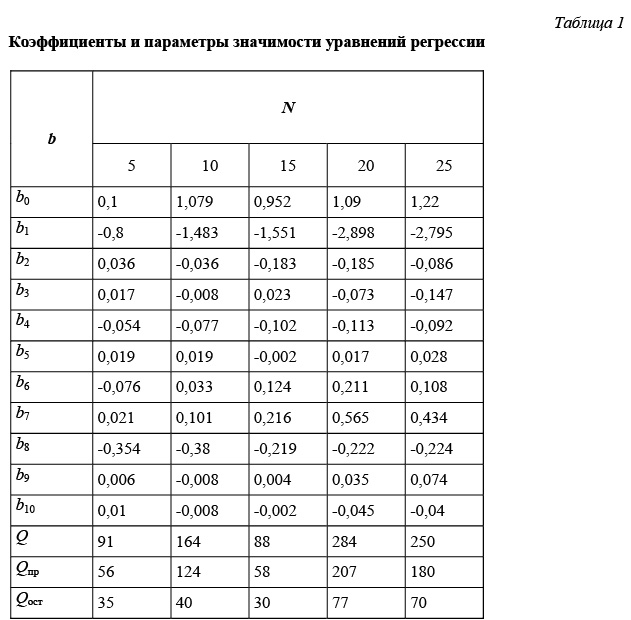
В таблице Q – общая сумма квадратов результативного признака, Qпр – общая сумма квадратов, характеризующая влияние признаков, Qост – остаточная сумма квадратов – влияние неучтенных факторов.

Полученные уравнения регрессии позволяют повысить точность оценки максимального правдоподобия введением поправки к оценке МП по формуле

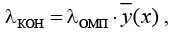                                                                                              (2)

где λкон – конечная оценка параметра распределения.

В исследованиях была проведена оценка эффективности построенных уравнений регрессии. Для каждой вновь сгенерированной выборки из общего количеством выборок V=3 000 по уравнениям регрессии (1) были рассчитаны поправки к оценке МП и конечная оценка параметра экспоненциального распределения по выражению (2).

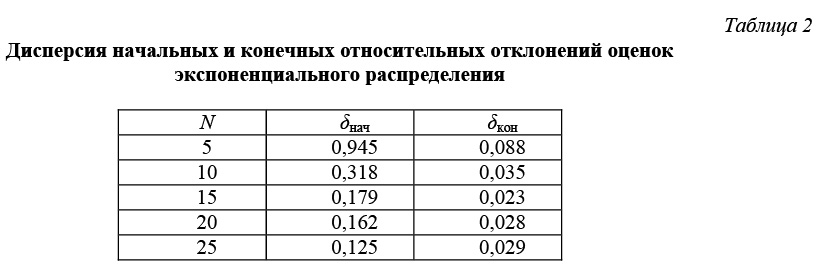
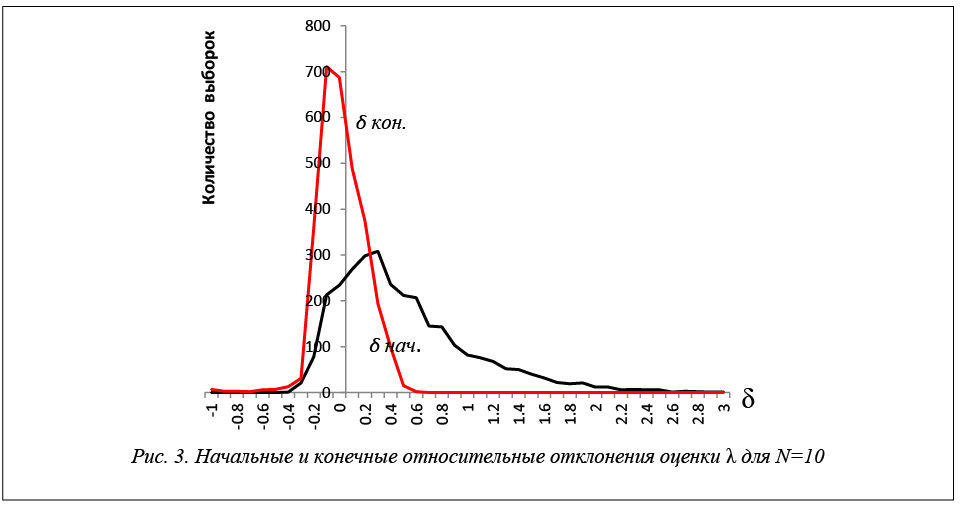
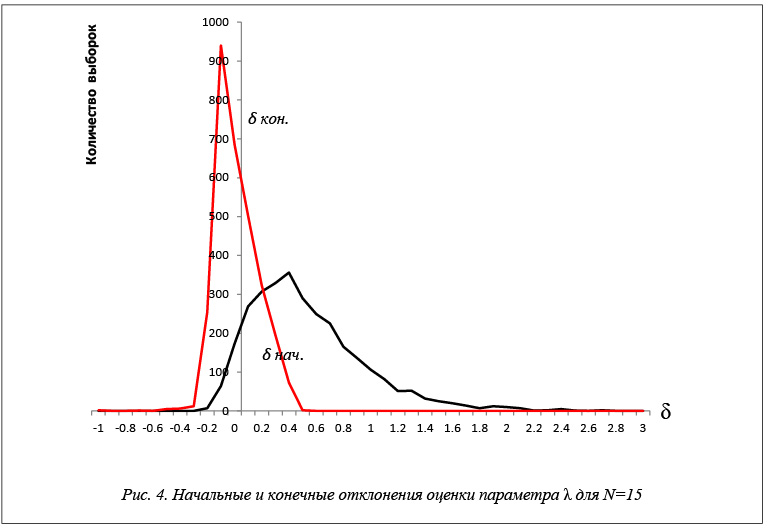
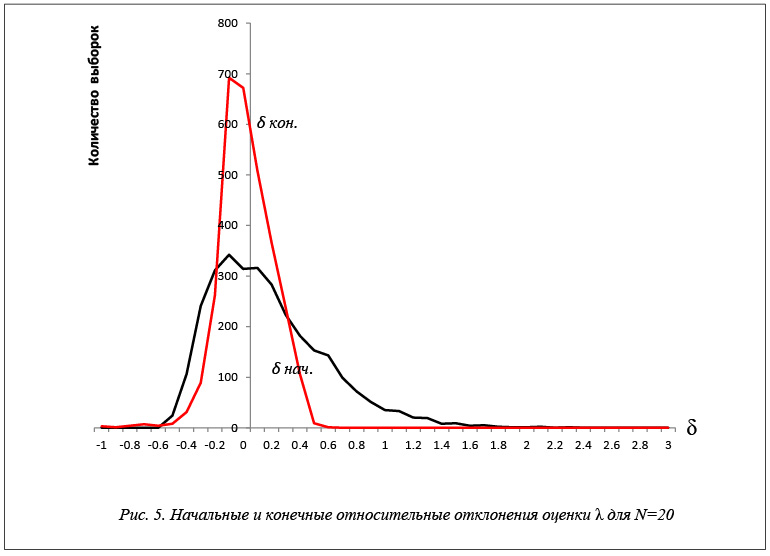
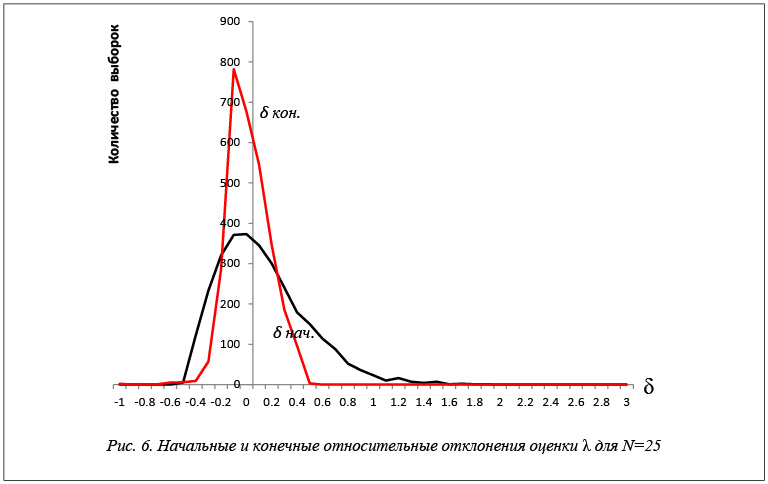
Результаты исследований эффективности применения построенных уравнений регрессии для экспоненциального закона распределения показаны в таблице 2 и на рисунках 2–6. На рисунках показаны
относительные отклонения оценок максимального правдоподобия от истинного значения. Применение разработанных моделей значительно повышает точность оценок максимального правдоподобия.

Литература

1. Барзилович Е.Ю. Модели технического обслуживания сложных систем. М.: Высш. школа, 1982. 231 с.

2. Шишко В.Б., Чиченев Н.А. Надежность технологического оборудования. М.: Изд-во МИСиС, 2012. 190 с.

3. Дорохов А.Н., Керножицкий В.А., Миронов А.Н., Шестопалова О.Л. Обеспечение надежности сложных технических систем. СПб: Лань, 2011. 348 с.

4. Ивченко Г.И., Медведев Ю.И. Математическая статистика. М.: ЛИБРОКОМ, 2014. 352 с.

5. Русин А.Ю., Абдулхамед М. Управление процессом испытания оборудования на надежность // Надежность. 2014. № 3. С. 27–34. 

6. Русин А.Ю., Абдулхамед М. Обработка информации в системе испытаний промышленного оборудования на надежность // Технологии техносферной безопасности. 2014. № 4. URL: http://ipb.mos.ru/ttb/2014-4/.