(Исследование выполнено при финансовой поддержке РФФИ, проект № 14-01-00579 а)
Актуальность исследований в области применения искусственных нейронных сетей (ИНС) подтверждается различными источниками [1, 2]. В настоящее время наблюдается значительный технологический рост в области проектирования нейронных сетей и нейрокомпьютеров. За последние годы открыто немало новых возможностей нейронных сетей, а работы в данной области становятся важным вкладом в промышленность, науку и технологии, имеют большое экономическое значение.
Данная статья посвящена программной реализация ИНС на основе ряда Вольтерра и является продолжением работы [3], в которой рассмотрены теоретические предпосылки метода динамического построения ИНС на основе ряда Вольтерра. Одна из задач, решаемых с помощью сети Вольтерра, – прогнозирование переменных во времени. Задача заключается в обработке ретроспективной информации об объекте, в установлении зависимости между состоянием этого объекта в будущем и состояниями в предыдущие периоды. В работе для апробации разработанного ПО используются данные о солнечной активности.
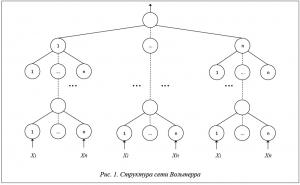
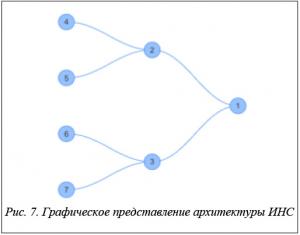
При решении задачи прогнозирования с помощью ИНС одной из главных проблем является выбор типа сети и ее архитектуры. Пример архитектуры сети Вольтерра для решения задачи прогнозирования показан на рисунке 1.
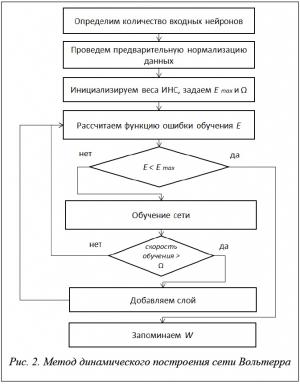
Процесс динамического построения и обучения ИНС Вольтерра можно представить в виде блок-схемы (рис. 2.)
Программная реализация
Информация о программных реализациях сетей Вольтерра в открытом доступе практически отсутствует. Найдена работа [4], в которой автор исследования решает задачу прогнозирования с помощью многослойного персептрона и сети Вольтерра. Для этого он проводит ряд экспериментов на ПО под названием Universal Neural Network Simulator. Данный продукт является внутренней разработкой, а значит, изучение его или использование в качестве составной части аналитического решения не представляется возможным. Исходя из этого, для проведения исследования было принято решение о создании собственной программной реализации сети Вольтерра.
В настоящее время одним из популярных языков программирования при решении задач, требующих обработки, визуализации, анализа данных, в том числе задач прогнозирования, является Python. Он предоставляет широкие возможности для прототипирования моделей за счет большого количества фреймворков и библиотек, реализующих множество популярных методов, алгоритмов и подходов к анализу данных. Кроссплатформенность позволяет разработанным на нем приложениям беспрепятственно работать на широко распространенных операционных системах (Windows, Linux и MacOS). Python поддерживает объектно-ориентированных подход (ООП), что позволяет построить модульную и масштабируемую архитектуру ПО. С этой точки зрения Python является наиболее подходящим языком программирования для реализации прототипа сети Вольтерра и метода динамического построения.
Для удобства, увеличения скорости написания программного кода и быстрой навигации по проекту будем использовать интегрированную среду разработки PyCharm [5]. Она предоставляет средства для анализа кода, графический отладчик и инструмент для запуска юнит-тестов и считается наиболее современной средой разработки для языка программирования Python. Графический интерфейс представлен на рисунке 3.
При разработке интеллектуальных систем возникает необходимость работы с данными (чтение и запись данных из файла, применение различных функций к данным и др.). Для задач такого рода наиболее удобной и функциональной библиотекой Python является NumPy [6], которая имеет такие бесспорные преимущества, как поддержка многомерных массивов (включая матрицы) и поддержка высокоуровневых математических функций, предназначенных для работы с многомерными массивами.
Таким образом, NumPy удовлетворяет всем необходимым требованиям для эффективной работы с данными.
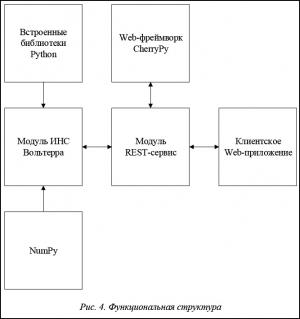
ПО спроектировано на основе ООП для удовлетворения требований модульности и масштабируемости. Данный подход в создании архитектуры приложений позволяет эффективно поддерживать проекты и увеличивает читаемость кода. Общая архитектура приложения представлена на рисунке 4.
ООП подразумевает логическое выделение классов, которые образуют иерархию наследований и исключают необходимость повторного написания кода.
Из структуры приложения видно (рис. 4), что модуль REST-сервис выполняет функцию связующего звена между клиентским приложением и программной реализацией математической модели. Данный модуль является web-сервером. К его функциям относятся получение запросов, обработка полученных данных и ответ клиенту по протоколу HTTP. Все функции работы сервера реализованы в CherryPy, благодаря этому логика обработки запросов и построение ответов прозрачны. Между тем данный модуль сам по себе не выполняет функции ИНС, а является вспомогательным, передающим параметры модулю ИНС Вольтерра. Рассмотрим модуль ИНС Вольтерра, так как он содержит основную логику построения, обучения и тестирования ИНС.
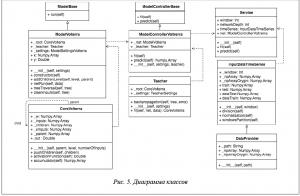
Точкой входа модуля ИНС Вольтерра является класс Service, он принимает все необходимые параметры, после чего создает объекты классов InputTimeSerries, ModelControllerVolterra и Teacher. Класс ModelControllerVolterra реализует логику работы ИНС Вольтерра, хранит и изменяет архитектуру ИНС. Диаграмма классов представлена на рисунке 5.
Архитектура ИНС строится из объектов класса CoreVolterra. Этот класс описывает сущность ядра Вольтерра, имеет ссылку на родительский объект и массив ссылок на дочерние объекты. Данные объекты имеют тип CoreVolterra. Таким образом, программная реализация архитектуры ИНС представлена в виде двунаправленно связанного дерева. Данный подход дает возможность создавать методы, вызываемые рекурсивно.
Класс Teacher реализует адаптивный алгоритм обучения ИНС. Свойства объектов данного класса: _root – ссылка на корневой объект дерева, net – объект ИНС Вольтерра, _settings – объект настроек алгоритма обучения.
Метод fit класса Teacher является реализацией алгоритма обратного распространения ошибки. Он принимает ссылку на корневой объект дерева сети и данные для обучения, после чего происходят расчет функции качества на каждом ядре и передача ее значения далее по структуре.
При необходимости запускается процесс генерации нового слоя. На первом этапе для каждого ядра, не имеющего дочерних объектов, запускается метод, который создают ядра. На втором этапе новые ядра привязываются к родительским объектам и становятся новым входным слоем.
Эксперименты
Для апробации программной реализации ИНС Вольтерра необходимо провести ряд экспериментов на реальных данных с подсчетом метрик качества. Рассмотрим данные о солнечной активности за период с января 1700 года по февраль 2015 года (всего 316 записей). Измерения проводились раз в календарный год на протяжении всего периода. Значения временного ряда представляют количество пятен на Солнце. При первичном анализе можно выявить явно выраженную периодичность солнечной активности в
11 лет, которая уже достаточно изучена, и установлен ряд закономерностей по амплитудам циклов [7–9].
Рассмотрим процесс решения задачи прогнозирования с помощью разработанного ПО.
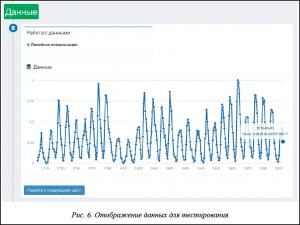
Шаг 1. Работа с данными.
На данном шаге происходят загрузка исходных данных и их визуализация в виде графика (рис. 6).
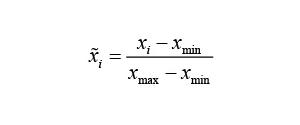
Возможна линейная нормализация данных по формуле
Данные для экспериментов автоматически подготовлены в соответствии с методом окон (windowing) [10], разбиты со смещением на вектора размерностью, равной количеству входов (табл. 1).
В таблице 1 через X обозначены входы нейронной сети, m – количество входов, i – порядковый номер входа нейронной сети i Î [1 … m], K – количество окон данных, равное N mod m + 1, N – количество наблюдений во временном ряду.
Шаг 2. Настройка сети.
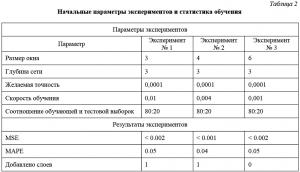
Далее производится установка параметров ИНС Вольтерра и алгоритма обучения. Значения по умолчанию для параметров представлены в таблице 2. Структура ИНС после применения параметров для первого эксперимента показана на рисунке 7.
Шаг 3. Результаты обучения.
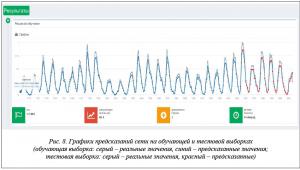
После обучения строятся графики, отражающие реальные и предсказанные значения на обучающей и тестовой выборках (рис. 8). Исследовалась зависимость качества прогноза от структуры нейронной сети и настроек алгоритма обучения. Статистика обучения и тестирования сети приведена в таблице 2.
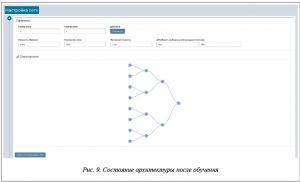
Из таблицы 2 видно, что ИНС Вольтерра справляется с задачей прогнозирования. Оптимальными значениями параметров алгоритма являются параметры эксперимента № 2. Среднеквадратичная ошибка (MSE) снизилась до тысячных, также в процессе обучения добавился слой сети. Таким образом, проведение эксперимента подтвердило обучающую и обобщающую способности данной программной реализации ИНС Вольтерра (рис. 9).
Результаты исследований показали, что качество прогнозирования зависит от скорости изменения ошибки – Ω, так как ее значение участвует в принятии решения о добавлении слоя:
Наилучшее качество прогноза достигается при Ω = 0,004. Также очевидно, что точность прогноза будет расти по мере увеличения эпох обучения.
Результаты прогнозирования солнечной активности могут быть использованы в оценке динамики водонасыщения поверхностных грунтов Ростовской области [11].
Литература
- Gatys L.A., Ecker A.S. and Bethge M. A neural algorithm of artistic style. 2015. arXiv preprint arXiv:1508.06576.
- Vinyals O., Le Q. A neural conversational model. 2015. arXiv:1506.05869.
- Пучков Е.В., Белявский Г.И. Разработка методов динамического построения искусственной нейронной сети на основе ряда Вольтерра и вейвлет-ядра // Вестн. Ростовского гос. ун-та путей сообщ. 2015. № 3. С. 127–131.
- Крючин О.В., Кондраков О.В. Прогнозирование временных рядов с помощью искусственных нейронных сетей и регрессионных моделей на примере прогнозирования котировок валютных пар // Исследовано в России. 2010. Т. 13. С. 953–967. URL: http://zhurnal.ape.relarn.ru/articles/2010/082.pdf/ (дата обращения: 31.10.2016).
- PyCharm. URL: https://www.jetbrains.com/pycharm/ (дата обращения: 31.10.2016).
- NumPy. URL: http://www.numpy.org/ (дата обращения: 31.10.2016).
- Schwabe H. Sonnenbeobachtungen im Jahre 1843. Astronomische Nachrichten, 1844, vol. 21, pp. 233–236.
- Витинский Ю.И., Копецкий М., Куклин Г.В. Статистика пятнообразовательной деятельности Солнца. М.: Наука, 1986. 296 с.
- Прист Э.Р. Солнечная магнитогидродинамика. М.: Мир, 1985. 589 с.
- Хайкин С. Нейронные сети: полный курс. 2-е изд. М.: Вильямс, 2006. 1104 с.
- Гридневский А.В. Комплексный подход к региональной оценке геологических опасностей территории Ростовской области // Сергеевские чтения: Инженерная геология и геоэкология. Фундаментальные проблемы и прикладные задачи: сб. тр. конф. 2016. Изд-во РУДН. С. 609–613.

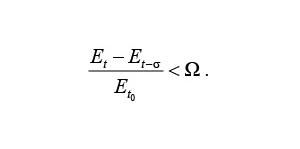
Комментарии