Современный этап развития сверхбольших интегральных схем (СБИС) требует разработки новых методов и подходов к их проектированию и технологиям производства. В настоящее время одной из основных технологических операций в общем процессе производства цифровых схем является литография, а одним из наиболее перспективных направлений дальнейшего развития литографии в рамках процесса производства СБИС – технология двойного шаблона. Данная технология дает возможность использовать имеющееся литографическое оборудование для изготовления СБИС с меньшей минимальной проектной нормой и с меньшей площадью кристалла. Это позволяет снизить стоимость производства современных СБИС и систем на кристалле.

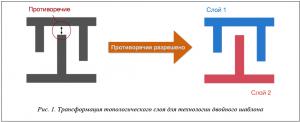
Основная задача технологии двойного шаблона заключается в декомпозиции исходного критического топологического слоя СБИС на два новых, в сумме содержащих исходный рисунок. При этом расстояние между элементами топологии в каждом из вновь полученных топологических слоев получается больше, чем в исходном слое топологии. На рисунке 1 показан результат трансформации исходного топологического слоя для технологии двойного шаблона.

Различные подходы к декомпозиции топологического слоя СБИС для технологии двойного шаблона рассмотрены в работах [1–3]. Следует заметить, что решение этой задачи требует значительных вычислительных ресурсов в силу огромного размера файлов описания топологии. Стремление сократить при этом время вычислений привело к разработке параллельных алгоритмов трансформации [4, 5]. Известно, что обнаружение и устранение ошибок в топологии кристалла СБИС на ранних стадиях его проектирования позволяет избежать множества проблем, связанных с затратами и сроками изготовления шаблонов, сократив тем самым время проектирования и производства СБИС [6]. Когнитивная аналитика и визуализация могут помочь исключить данную проблему, так как решают задачу извлечения ценности из большого объема данных и преобразования информации в удобный для восприятия и познания человеком формат. Такие технологии находятся на стыке информатики и когнитивной науки [7–9]. В свою очередь, когнитивные методы визуализации позволяют упростить интеркогнитивные коммуникации между высокопроизводительными вычислительными системами и проектировщиками СБИС, тем самым сокращая временные затраты на анализ.

В работе [10] рассмотрено применение когнитивных технологий для решения задач в наноинженерии, в том числе задачи проектирования топологических слоев СБИС. Показано, что последние достижения в области когнитивных технологий можно применять в системах автоматизации проектирования (САПР) СБИС.

В работе [11] предложены и рассмотрены параллельные алгоритмы для декомпозиции слоев с неманхэттенской геометрией, реализованные в программе ParallelDPLayout Migrator. В этой программе для описания графовых моделей применен язык DOT, а для визуализации графов использовано ПО с открытым исходным кодом GraphViz [12]. Программа была протестирована с использованием библиотек Nangate Open Cell Library и Lower Power Open Cell Library [13, 14]. В работе [15] теоретически обосновано применение когнитивной аналитики в САПР СБИС. В работе [16] показаны результаты применения предложенного подхода для регулярной топологии. В данной работе рассматривается возможность применения разработанных подходов для анализа топологических слоев с нерегулярной топологией, которая значительно труднее поддается этому процессу.

Когнитивная визуализация проблемных участков топологического слоя

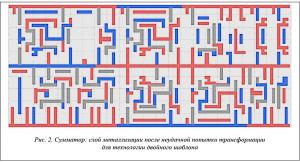
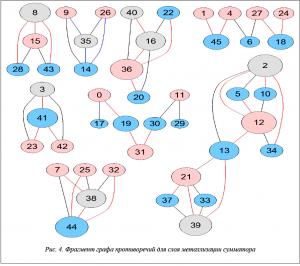
В качестве примера выбран слой металлизации библиотечного элемента «сумматор». На рисунке 2 представлен фрагмент его топологического слоя, для которого попытка трансформации для технологии двойного шаблона закончилась неудачно. Представленный фрагмент состоит из 286 полигонов. Соответствующий ему граф противоречий, который содержит 286 вершин и 471 ребро, приведен на рисунке 3. Каждая вершина графа соответствует определенному полигону, а ребро – противоречию между парой полигонов.

На рисунках 2–5 полигоны первого слоя и соответствующие им вершины графа противоречий после декомпозиции показаны розовым цветом, полигоны второго слоя и соответствующие им вершины графа противоречий – синим. Полигоны и соответствующие им вершины графа противоречий, которые не удалось окрасить и, следовательно, разнести по слоям, показаны серым цветом. В первый слой получилось отнести 137 полигонов, во второй – 84, 65 полигонов разнести не удалось, так как они попали в нечетные циклы графа противоречий.

В работах [15, 16] была предложена следующая классификация противоречий:

– внутренние: противоречия между полигонами в рамках одного экземпляра ячейки (ребра отображаются черным цветом);

– противоречия ячейки: противоречия между полигонами из разных экземпляров одной̆ и той же ячейки (ребра отображаются синим цветом);

– внешние: противоречия между полигонами, которые относятся к разным ячейкам (ребра отображаются красным цветом как наиболее сложный вид противоречий для разрешения).

В работе [15] для каждого противоречия выбран определенный коэффициент, который влияет на размер радиуса вершины графа противоречий. Благодаря этому можно быстро найти полигоны и, соответственно, участки топологического слоя с наибольшим количеством противоречий.

В работе [16] предложен подход к кластеризации графа противоречий на основании данных о том, к каким стандартным ячейкам и их экземплярам относится тот или иной полигон. В предложенной модели вершины графа противоречий распределяются между кластерами согласно исходной иерархии библиотечных элементов. Кластеры визуализируются в виде прямоугольников.

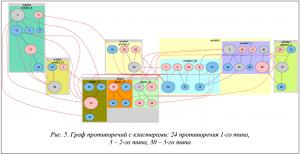
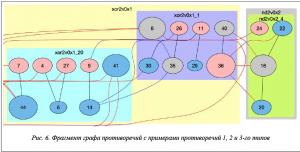
На основании рисунков 2 и 4 достаточно сложно определить, какие библиотечные фрагменты исходного топологического слоя привели к неразрешимым противоречиям. Однако на рисунке 3 уже видны участки топологии с наибольшим количеством конфликтов. Для дальнейшего анализа выбран один из таких участков топологического слоя. На рисунке 4 представлен небольшой фрагмент графа противоречий, а на рисунке 5 – результат кластеризации на основе исходной иерархии библиотечных элементов для выбранного фрагмента.

На рисунке 5 большие кластеры соответствуют элементам библиотеки фрагментов топологии СБИС, а меньшие – конкретным элементам данного фрагмента. Предлагаемая модель визуализирует геометрические примитивы (полигоны), из которых состоит топологический слой, и при этом не теряет связь с их исходной иерархией.

На рисунке 6 приведены примеры противоречий всех типов согласно предлагаемой классификации. Ребра, соответствующие противоречиям 1-го типа (противоречия между парами полигонов {#7, #44}, {#4, #6}, {#6, #27}, {#9, #14}, {#30, #11}, {#35, #26}, {#29, #11}, {#36, #40}, {#16, #20}, {#16, #20}), выделены черным цветом. Ребра, соответствующие противоречиям 2-го типа (противоречия между полигонами {#9, #35}, {#14, #35}, {#14, #26}), – синим цветом. Ребра, соответствующие противоречиям 3-го типа (противоречия между полигонами {#40, #16}, {#36, #22}, {#36, #16}, {#36, #20}), – красным цветом.

Несмотря на большое количество противоречий и их уникальность в силу того, что геометрия не регулярная, предлагаемый подход все равно применим и позволяет достаточно быстро находить проблемные участки топологического слоя и именно на них концентрировать внимание проектировщика СБИС. В зависимости от количества противоречий того или иногда типа и сложности их разрешения в каждом конкретном случае можно принять соответствующее решение: от изменения компоновки или замены одной стандартной ячейки на другую до изменения параметров технологического процесса, если это представляется выполнимым в силу возможных ограничений существующего оборудования.

Заключение

Стоит заметить, что предложенный подход к когнитивной аналитической поддержке процесса проектирования топологических слоев СБИС, основанный на использовании когнитивных технологий, упрощает и ускоряет сам процесс проектирования. Все графы (рисунки 3–6) были получены в результате
работы программы ParallelDPLayout Migrator и визуализированы при помощи библиотеки с открытым исходным кодом GraphViz [12].

Важным результатом работы является то, что кластеризация и представление противоречий с использованием когнитивной графики упрощают процесс принятия проектных решений при проектировании топологии СБИС. Предложенный подход применим как для проектирования СБИС, так и для анализа количественных характеристик качества ее топологии. Например, следует заметить, что большое количество противоречий 2-го и 3-го типов показывает степень связности библиотечных элементов в топологии СБИС, а это, в свою очередь, сильно усложняет процесс их устранения.

Исследование выполнено при частичной финансовой поддержке РФФИ в рамках научного проекта
№ 16-37-00254 мол_а.

Литература

1. Ghaida R.S., Agarwal K.B., Nassif S.R., Xin Y., Liebmann L.W., Gupta P. Layout decomposition and legalization for double-patterning technology. Computer-Aided Design of Integrated Circuits and Systems, IEEE Transactions, 2013, vol. 2, pp. 202–215.
2. Zigang X., Yuelin D., Hongbo Z., Wong M.D.F. A polynomial time exact algorithm for overlay-resistant self-aligned double patterning (SADP) layout decomposition. Computer-Aided Design of Integrated Circuits and Systems, IEEE Transactions, 2013, vol. 8, pp. 1228–1239.
3. Шахнов В.А., Зинченко Л.А., Резчикова Е.В., Аверьянихин А.Е. Алгоритм преобразования топологии субмикронных СБИС // Вестн. МГТУ им. Н.Э. Баумана. 2011. С. 20–28.
4. Шахнов В.А., Зинченко Л.А., Верстов В.А. Трансформация топологии субмикронных СБИС для технологии двойного шаблона // Микроэлектроника. 2013. Т. 42. № 6. С. 427–439.
5. Hailong Y., Yici C., Wei Z. WIPAL: window-based parallel layout decomposition in double patterning lithography. Proc. IEEE Intern. Conf. on Solid-State and Integrated Circuit Technology (ICSICT), 2012, pp. 1–4.
6. Patterson O.D., Ryan D.A., Monkowski M.D., NguyenNgoc D., Morgenfeld B., Chung-ham Lee, Chieh-Hung Liu, Chiming Chen, Shih-Tsung Chen. Early Detection of Systematic Patterning Problems for a 22nm SOI Technology using E-Beam Hot Spot Inspection. Proc. SEMI2013, 2013, pp. 295–300.
7. Baranyi P., Csapo A. Definition and synergies of cognitive infocommunications. Acta Polytechnica Hungarica, 2012, vol. 9, pp. 67–83.
8. Persa G., Csapo A., Baranyi P. CogInfoCom systems from an interaction perspective – a pilot application for etocom. Jour. ACIII, 2012, vol. 16, no. 2, pp. 297–304.
9. Sallai G. The cradle of cognitive infocommunications. Acta Polytechnica Hungarica, 2012, vol. 9, no. 1, pp. 171–181.
10. Shakhnov V., Zinchenko L., Makarchuk V., Verstov V. Heterogeneous knowledge representation for VLSI systems and MEMS design. Proc. 2013 IEEE 4th Intern. Conf. Cognitive Infocommunications (CogInfoCom), 2013, pp. 189–194.
11. Shakhnov V.A., Zinchenko L.A., Verstov V.A. Parallel Algorithm of SOI layout decomposition for double patterning lithography on high-performance computer platforms. Technological innovation for collective awareness systems. IFIP Advances in Information and Communication Technology, 2014, vol. 423, pp. 543–550.
12. Graphviz. 2015. URL: http://www.graphviz.org/ (дата обращения: 20.10.2017).
13. Zinchenko L.A., Makarchuk V.V., Verstov V.A. SOI layout decomposition for double patterning lithography on high-performance computer platforms. Proc. SPIE 9440, Intern. Conf. on Microand Nano-Electronics 2014. URL: http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=2086493 (дата обращения: 20.10.2017).
14. NanGate, Inc. NanGate 45nm Open Cell Library. 2008. URL: http://www.nangate.com/?page_id=2325 (дата обращения: 20.10.2017).
15. Верстов В.А., Зинченко Л.А., Макарчук В.В., Шахнов В.А. Когнитивная визуализация противоречий в задачах трансформации топологического слоя СБИС для технологии двойного шаблона // Проблемы разработки перспективных микро- и наноэлектронных систем (МЭС). 2016. № 1. С. 158–164.
16. Шахнов В.А., Зинченко Л.А., Макарчук В.В., Верстов В.А. Система визуализации и аналитической поддержки проектирования топологии СБИС для технологии двойного шаблона // Программные продукты и системы. 2016. № 2. С. 100–104.