Первая работа на тему групповых технологий в производстве была написана в 1925 году [1]. В России такое исследование было представлено только в 1933 году [2]. Один из главных вопросов при рассмотрении групповых технологий – это поиск оптимального распределения станков и деталей в производственные ячейки таким образом, чтобы максимизировать обработку внутри цехов и минимизировать
передвижение деталей между цехами. Эта задача называется задачей о формировании производственных ячеек (ЗФПЯ) [3]. Максимизация групповой эффективности считается хорошей целевой функцией для этой задачи, так как она комбинирует обе цели [4].

В работе [5] представлен подход, основанный на анализе потока продукции, для решения ЗФПЯ, описаны групповые технологии и ЗФПЯ. Было создано множество эвристических алгоритмов для решения этой задачи [6–9] и почти ни одного точного с незаданным количеством цехов и целевой функцией, основанной на групповой эффективности. В [10] рассмотрен один из простейших вариантов ЗФПЯ – задача о распределении станков, в которой необходимо распределить станки по заданному количеству цехов, минимизируя общее расстояние Хэмминга между станками внутри цехов. Представлен точный алгоритм A* для такой формулировки ЗФПЯ, предложен метод ветвей и границ для ЗФПЯ с нефиксированным количеством цехов, с ограничением количества станков внутри цеха и целевой функцией, максимизирующей размеры так называемых взаимно разделяемых ячеек. В работах [11, 12] также представлен метод ветвей и границ для задачи распределения станков.

Один из существующих точных подходов для ЗФПЯ с бикластеризацией станков и деталей и групповой эффективностью в качестве целевой функции был описан в [13]. Авторы предложили свести задачу дробного программирования ЗФПЯ к нескольким задачам целочисленного линейного программирования (ЦЛП) с использованием метода Динкельбаха [14] и решить каждую такую задачу с помощью пакета CPLEX. Однако они рассматривали эту задачу с заранее заданным количеством ячеек, что является упрощением. Такая же упрощенная формулировка ЗФПЯ рассматривается в [15].

Точный алгоритм для ЗФПЯ в ее исходной формулировке с переменным числом ячеек и с групповой эффективностью в качестве целевой функции представлен в [16]. В работе [17] рассмотрена ЗФПЯ с переменным числом ячеек как задача двухкритериальной оптимизации и разработан точный алгоритм, который находит Парето-фронт решений.

В настоящей статье предлагается эффективный алгоритм ветвей и границ для ЗФПЯ с переменным числом ячеек и с целевой функцией групповой эффективности. Чтобы получить хорошую верхнюю границу, задача линеаризуется с применением подхода Динкельбаха. Для вычисления верхней границы предлагается релаксация линеаризованной задачи, которую можно эффективно решить за полиномиальное время. Удалось получить оптимальные решения для 24 из 35 тестовых задач. Начальное исследование с более простым подходом и меньшими результатами отражено в [18].

Следует отметить, что ЗФПЯ в своей классической формулировке представляет собой задачу бикластеризации, в которой станки и детали одновременно группируются в ячейки. Таким образом, предложенный подход может быть также применен к задачам бикластеризации в интеллектуальном анализе данных [19].

Описание задачи

Целью ЗФПЯ является нахождение оптимального разбиения станков и деталей на группы (производственные цеха, ячейки) для сведения к минимуму перемещения деталей из одного цеха в другой и максимизации их обработки внутри цехов. Данные для задачи представляют собой матрицу A, которая содержит нули и единицы. Размер матрицы равен m × p, где m – количество станков, а p – количество деталей. Элемент a_ij матрицы равен единице, если деталь j должна обрабатываться на станке i. Необходимо минимизировать количество нулей внутри ячеек (недогрузка станков) и количество единиц вне ячеек (перемещение деталей между цехами).

В литературе известно несколько целевых функций, объединяющих эти две цели. Целевая функция, которая обеспечивает хорошее сочетание этих целей и широко используется в литературе, – это групповая эффективность, предложенная в работе [4]:

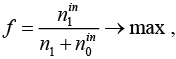                               (1)

где n₁ – количество единиц в исходной матрице; n₁ⁱⁿ – количество единиц внутри ячеек; n₀ⁱⁿ – количество нулей внутри ячеек.

Представим математическую модель для ЗФПЯ (см. также [16]).

Переменные:

      (2)

      (3)

 

Целевая функция:

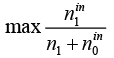                                       (4)

Ограничения:

    Здесь c = min(m, p) – максимально возможное количество ячеек. Ограничения (7) и (8) требуют, чтобы каждый станок и каждая деталь относились ровно к одной ячейке. Ограничения (9) и (10) требуют, чтобы не было ячеек, которые содержат только станки или только детали.

Для линеаризации целевой функции используем метод Динкельбаха и рассмотрим следующую целевую функцию: 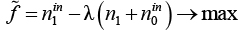, где 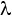 на каждой итерации равно текущему лучшему решению для исходной ЗФПЯ. На первой итерации  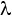равно значению групповой эффективности в тривиальном решении, в котором все станки и детали назначены в одну большую ячейку:

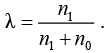
Чтобы найти оптимальное решение 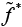 линеаризованной задачи, применим метод ветвей и границ.

Если оптимальное решение 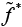 равно нулю, то для любого возможного решения  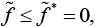следовательно,

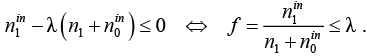
Это означает, что 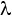 является оптимальным решением для ЗФПЯ, так как любое допустимое решение 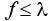. В этом случае останавливаем алгоритм.

Если 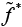>0, тогда

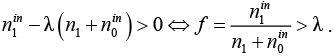
Это свидетельствует о том, что найденное решение f лучше текущего лучшего решения 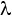. Заметим, что нет необходимости находить оптимальное 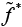, рассматривая все ветки в методе ветвей и границ – любое допустимое решение 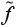>0 может быть использовано. В этом случае устанавливаем  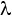= f и повторно запускаем решение линеаризованной задачи методом ветвей и границ с новым значением .

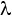Заметим, что 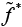 не может быть отрицательным, так как

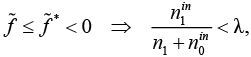
но уже есть допустимое решение f = .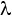

Метод ветвей и границ

Псевдокод алгоритма приведен далее в алгоритмах 1–4. Для решения линеаризованной задачи 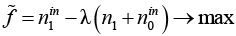 предлагается метод ветвей и границ. Ветвление происходит по станкам, а граница вычисляется как решение полиномиальной релаксации задачи. Для ускорения алгоритма не следует искать оптимальное  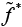решение на каждом шаге метода Динкельбаха (см. алгоритм 1), а как только найдено допустимое решение 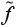>0 (строка 7 алгоритма 2), надо остановиться.

Для описания ветвей используем вектор M (1 × m), который содержит распределение станков по ячейкам. Элемент M_i определяет, в какую ячейку назначен станок i. 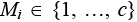, где c = min(m, p). Например, M = (1, 2, 3, 1, 0, …,0) означает, что станки 1 и 4 назначены в ячейку 1, станок 2 – в ячейку 2, станок 3 – в ячейку 3, а другие станки еще не распределены.

Алгоритм 1 использует подход Динкельбаха. Текущее лучшее распределение станков сохраняется в векторе M^*, значение целевой функции – в переменной f ^*, а количество единиц и нулей внутри ячеек – в переменных 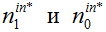. Текущее лучшее решение линеаризованной задачи сохраняется в переменной 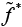. Так как числа с плавающей точкой имеют ограниченную точность, сравниваем  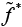с величиной 0,00001 вместо нуля. Это значение достаточно мало, чтобы гарантировать 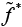= 0, так как

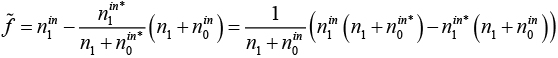
и все значения в скобках целые. Поэтому 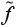 будет положительным, только если

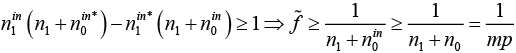
Таким образом, для любого решения, включая текущее лучшее 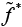, значение будет положительным, только если оно не меньше 1/mp.

В алгоритме 1 начальное решение исходной задачи выбирается равным 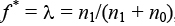, что означает распределение всех станков и деталей в одну ячейку. Далее для каждой итерации, пока  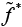не ноль, решаем линеаризованную задачу с новым значением 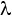, используя метод ветвей и границ. Когда  становится нулем, останавливаем алгоритм, так как это означает, что текущее лучшее решение f * =  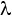является оптимальным для исходной задачи.

Ветвление. Пусть k – количество ячеек в текущем частичном решении. Алгоритм начинает с распределения первого станка в ячейку 1. Потом он использует следующий нераспределенный станок и определяет его в существующие ячейки 1, ..., k или создает новую (k+1) для этого станка. Например, в вершине, когда M = (1, 2, 3, 1, 0, …,0), получим 4 ветви: (1, 2, 3, 1, 1, 0, …,0), (1, 2, 3, 1, 2, 0, …,0), (1, 2, 3, 1, 3, 0, …,0) и (1, 2, 3, 1, 4, 0, …,0) (строка 2 алгоритма 2).

Листья дерева поиска содержат полные решения, а остальные вершины – частичные. Полное дерево поиска без использования границ зависит только от количества станков. Заметим, что ячейка k + 2 в частичном решении никогда не используется, если ячейка k + 1 еще не была использована в текущем решении (последняя строка алгоритма 2). Это гарантирует, что не будут рассматриваться одинаковые решения, которые различаются только нумерацией ячеек.

Следуем сильной стратегии ветвления: перед тем как выбрать ветвь для следующего шага, подсчитаем верхнюю границу каждой ветви и перейдем в ту, которая дает максимальное значение (строка 4 алгоритма 2).

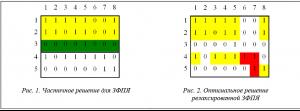
Верхняя граница . Чтобы получить оценку сверху для данного частичного решения, предлагается релаксация линеаризованной задачи ФПЯ, которая может быть решена с помощью полиномиального алгоритма. Релаксированная задача формулируется следующим образом. Дано частичное решение, в котором только некоторые из станков уже назначены в ячейки. Например, на рисунке 1 станки 1 и 2 назначаются в ячейку 1, а станок 3 – в ячейку 2. Необходимо назначить все детали в существующие ячейки или в новую ячейку. В релаксированной задаче допускаем независимое назначение деталей: например, деталь 1 может быть назначена в ячейку 1 со станками 1, 2 (уже назначенными в ячейку 1), а также со станком 4, а деталь 8 может быть назначена в ту же самую ячейку 1 с другими станками – 1, 2 и 5.

В примере из рисунка 1 деталь 1 может быть назначена в ячейку 1 с двумя единицами от станков 1 и 2 и третьей единицей от станка 4, который потенциально может принадлежать и ячейке 1. Поэтому в лучшем случае назначение детали 1 в ячейку 1 даст 3 единицы и 0 нулей внутри ячеек. Обозначим этот вариант как (3, 0). Также назначение детали 1 в ячейку 2 дает в лучшем случае 1 единицу (от станка 4) и 1 ноль (от станка 3) внутри ячеек. Назначение в новую ячейку дает 1 единицу (от станка 4) и 0 нулей внутри ячеек. Итак, есть 3 альтернативы (3,0), (1,1) и (1,0) для детали 1.

Для выбора между двумя альтернативами надо посчитать их вклад в целевую функцию 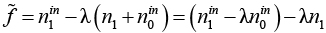. Так как 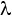n₁ – константа, очевидно, что вклад альтернативы (a, b) (где 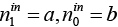), равен a – 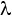b. Пусть 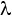= 0.5 в нашем примере. Тогда для детали с альтернативами (2,1), (1,1), и (1,0) получаем вклады 1.5, 0.5, и 1.0 соответственно. Значит, альтернатива (2,1) наилучшая (см. алгоритм 3).

Оптимальное решение для релаксированной задачи показано на рисунке 2. Это решение недопустимо для исходной ЗФПЯ, потому что из-за независимого распределения получены непрямоугольные ячейки, пересекающиеся друг с другом. Так как это оптимальное решение релаксированной задачи, оно дает верхнюю границу для исходной задачи: UB = 18.5 – 0.5⋅20 = 8.5.

Далее находим наилучшее назначение всех деталей в ячейки и вычисляем целевую функцию как сумму вкладов деталей минус 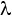n₁, что дает нам верхнюю границу. Однако после такого назначения могут получиться ячейки со станками, но без деталей. Такие ячейки не допускаются в классической формулировке ЗФПЯ. Каждая ячейка, имеющая станки, должна иметь хотя бы одну деталь. Целевая функция линеаризованной задачи линейна, а назначение одной детали вносит вклад, не зависящий от другой детали. Это означает, что мы можем сначала выбрать оптимально одну деталь для каждой ячейки, максимизируя общий вклад в целевую функцию этих выбранных деталей, а затем назначить каждую оставшуюся деталь в лучшую для нее ячейку без каких-либо ограничений. Очевидно, что задача выбора одной детали для каждой ячейки эквивалентна линейной задаче о назначениях (ЗН), в которой стоимость назначения равна вкладу детали в целевую функцию со знаком «минус», то есть 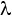b – a (см. алгоритм 3). Чтобы сбалансировать матрицу затрат (сделать ее квадратной) в этой задаче, добавляем фиктивные ячейки, для которых все стоимости назначения равны – .

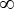Для решения задачи о назначениях применяем алгоритм Йонкера Волгенанта [20]. Перед запуском этого алгоритма проверяем решение релаксированной задачи, в котором могут быть ячейки без деталей. Если таких ячеек нет или эта верхняя граница уже позволяет отбросить текущую ветвь, не решаем задачу о назначениях, чтобы уменьшить время вычислений.

В примере на рисунке 2 ячейка 2 содержит станок 3, но не имеет деталей. Поэтому нужно назначить одну деталь каждой ячейке, решая задачу о назначениях. Матрица затрат для нашего примера представлена на рисунке 3 (ячейки 4, 5, 6, 7, 8 добавляются для балансировки матрицы).

Матрица стоимостей для задачи о назначениях

Одним из оптимальных решений этой задачи о назначениях является назначение детали 1 в ячейку 1, детали 5 в ячейку 2 и детали 7 в ячейку 3 с вкладом в верхнюю границу, равным 3 + 2 + 2 = 7. Каждая другая деталь назначается без каких-либо ограничений в ячейку, где она дает максимальный вклад в верхнюю границу. Таким образом, получаем UB = 7 + (2 + 1.5 + 3 + 1 + 3)-0.5*20=7.5.

Заметим, что, когда все станки распределены по ячейкам, решение релаксированной задачи с применением задачи о назначениях дает допустимое решение для исходной задачи. Поэтому получается оптимальное решение 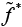=UB.

Результаты

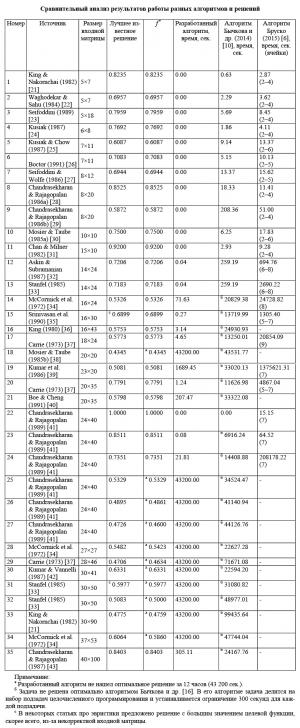
Представленный алгоритм ветвей и границ находит точное решение для 24 из 35 известных тестовых примеров из литературы, а для остальных примеров – решение, близкое к лучшему известному решению. Результаты представлены в таблице. Все вычисления были произведены на Intel Core i7 с 16Gb RAM. Как видим, разработанный алгоритм эффективнее подходов, предложенных в работах [15, 16], даже если не учитывать, что в работе [16] в качестве начального решения используется лучшее известное решение, а алгоритм Бруско [15] решает тестовые задачи только для нескольких фиксированных значений числа ячеек. Для результатов Бруско [15] в таблице представлено общее время, затрачиваемое на решение каждого примера для всех рассматриваемых значений числа ячеек и получение начального решения эвристикой.

На основании этих результатов можно сказать, что описываемый алгоритм работает быстрее для задач с высоким оптимальным значением целевой функции. Благодаря эффективной стратегии ветвления алгоритм быстро находит хорошие решения, и, если оптимальное значение целевой функции велико, то многие ветви отбрасываются, потому что предложенная верхняя граница обычно намного более точная для таких случаев. Например, задачи 20 и 21 имеют одинаковый размер входной матрицы, но задача 20
с оптимальным решением 0,7791 решается в течение 2 секунд, в то время как задача 21 с точным решением 0,5798 требует 207 секунд.

Заключение

В статье рассматривается классическая формулировка задачи о формировании производственных ячеек, которая имеет высокую вычислительную сложность из-за следующих факторов:

– целевая функция групповой эффективности – это дробная функция, которая делает ее задачей целочисленного дробного программирования;

– это задача бикластеризации, в которой необходимо группировать одновременно станки и детали
в производственные ячейки;

– оптимальное количество ячеек заранее неизвестно.

Из-за этих трудностей в большинстве работ, посвященных ЗФПЯ с переменным числом ячеек и целевой функцией групповой эффективности, представлены эвристические алгоритмы, а точные подходы в литературе практически отсутствуют. В данном точном алгоритме применяется процедура Динкельбаха и рассматривается линеаризованная задача для преодоления первой трудности. Чтобы избежать второй трудности в разработанном алгоритме ветвей и границ, сначала назначаем только станки в ячейки,
а затем получаем верхнюю границу с помощью решения релаксированной полиномиальной задачи. В листовых узлах дерева поиска, когда все станки назначены в ячейки, релаксированная задача становится эквивалентной исходной линеаризованной задаче, и получается оптимальное решение с помощью полиномиального алгоритма. Третья трудность заставляет рассматривать гораздо больше ветвей, чем это было бы при фиксированном числе ячеек. Если в первом точном подходе [18] удалось точно решить только 14 тестовых задач, то новый алгоритм позволяет решить еще 10 задач больших размеров.

Исследование выполнено в лаборатории ЛАТАС, НИУ ВШЭ и поддержано грантом РНФ 14-41-00039.

Литература

1. Flanders R.E. Design manufacture and production control of a standard machine. Transactions of ASME, 1925, vol. 46, pp. 691–738.

2. Митрофанов С.П. Научные основы групповых технологий. Л.: Лениздат, 1933. 435 с.

3. Goldengorin B., Krushinsky D., Pardalos P.M. Cell formation in industrial engineering. Theory, algorithms and experiments. Springer, Optimization and Its Applications, 2013, vol. 79, 206 p.

4. Kumar K.R., Chandrasekharan M.P. Grouping efficacy: A quantitative criterion for goodness of block diagonal forms of binary matrices in group technology. Intern. Jour. Production Research, 1990, vol. 28, no. 2,
pp. 233–243.

5. Burbidge J.L. The new approach to production. Prod. Eng., 1961, pp. 3–19.

6. Goncalves J.F., Resende M.G.C. An evolutionary algorithm for manufacturing cell formation. Computers & Industrial Engineering, 2004, vol. 47, pp. 247–273.

7. James T.L., Brown E.C., Keeling K.B. A hybrid grouping genetic algorithm for the cell formation problem. Computers & Operations Research, 2007, vol. 34, no. 7, pp. 2059–2079.

8. Bychkov I., Batsyn M., Sukhov P., Pardalos P.M. Heuristic algorithm for the cell formation problem. In: Models, Algorithms, and Technologies for Network Analysis. Springer Proc. Mathematics & Statistics, 2013, vol. 59, pp. 43–69.

9. Paydar M.M., Saidi-Mehrabad M. A hybrid genetic-variable neighborhood search algorithm for the cell formation problem based on grouping efficacy. Computers & Operations Research, 2013, vol. 40, no. 4,
pp. 980–990.

10. Kusiak A., Boe J.W., Cheng C. Designing cellular manufacturing systems: branch-and-bound and A* approaches. IIE Transactions, 1993, vol. 25, no. 4, pp. 46–56.

11. Spiliopoulos K., Sofianopoulou S. An optimal tree search method for the manufacturing systems cell formation problem. Europ. Jour. Operational Research, 1998, vol. 105, pp. 537–551.

12. Arkat J., Abdollahzadeh H., Ghahve H. A new branch-and-bound algorithm for cell formation problem. Applied Mathematical Modelling, 2012, vol. 36, pp. 5091–5100.

13. Elbenani B., Ferland J.A. Cell Formation Problem Solved Exactly with the Dinkelbach Algorithm. Montreal, Quebec, 2012, pp. 1–14.

14. Dinklebach W. On nonlinear fractional programming. Management Science, 1967, vol. 13, pp. 492–498.

15. Brusco J.M. An exact algorithm for maximizing grouping efficacy in part-machine clustering. IIE Transactions, 2015, vol. 47, no. 6, pp. 653–671.

16. Bychkov I., Batsyn M., Pardalos P. Exact model for the cell formation problem. Optimization Letters, 2014, vol. 8, no. 8, pp. 2203–2210.

17. Zilinskas J., Goldengorin B., Pardalos P.M. Pareto-optimal front of cell formation problem in group technology. Jour. Global Optimization, 2015, vol. 61, no. 1, pp. 91–108.

18. Utkina I., Batsyn M., Batsyna E. A branch and bound algorithm for a fractional 0-1 programming problem. Lecture Notes in Computer Science, 2016, vol. 9869, pp. 244–255.

19. Busygin S., Prokopyev O., Pardalos P.M. Biclustering in data mining. Computers & Operations Research 2008, vol. 35, no. 9, pp. 2964–2987.

20. Jonker R., Volgenant A.A. Shortest augmenting path algorithm for dense and sparse linear assignment problems. Computing, 1987, vol. 38, pp. 325–340.

21. King J.R., Nakornchai V. Machine-component group formation in group technology: Review and extension. Intern. Jour. Production Research, 1982, vol. 20, no. 2, pp. 117–133.

22. Waghodekar P.H., Sahu S. Machine-component cell formation in group technology MACE. Intern. Jour. Production Research, 1984, vol. 22, pp. 937–948.

23. Seifoddini H. A note on the similarity coefficient method and the problem of improper machine assignment in group technology applications. Intern. Jour. Production Research, 1989, vol. 27 no. 7, pp. 1161–1165.

24. Kusiak A. The generalized group technology concept. International Journal of Production Research, 1987, vol. 25, no. 4, pp. 561–569.

25. Kusiak A., Chow W.S. Efficient solving of the group technology problem. Jour. of Manufacturing Systems, 1987, vol. 6, no. 2, pp. 117–124.

26. Boctor F.F. A linear formulation of the machine-part cell formation problem. Intern. Jour. Production Research, 1991, vol. 29, no. 2, pp. 343–356.

27. Seifoddini H., Wolfe P.M. Application of the similarity coefficient method in group technology. IIE Transactions, 1986, vol. 18, no. 3, pp. 271–277.

28. Chandrasekharan M.P., Rajagopalan R. MODROC: An extension of rank order clustering for group technology. Intern. Jour. Production Research, 1986, vol. 24, no. 5, pp. 1221–1233.

29. Chandrasekharan M.P., Rajagopalan R. An ideal seed non-hierarchical clustering algorithm for cellular manufacturing. Intern. Jour. Production Research, 1986, vol. 24, no. 2, pp. 451–464.

30. Mosier C.T., Taube L. The facets of group technology and their impact on implementation. OMEGA, 1985, vol. 13, no. 6, pp. 381–391.

31. Chan H.M., Milner D.A. Direct clustering algorithm for group formation in cellular manufacture. Jour. Manufacturing Systems, 1982, vol. 1, no. 1, pp. 64–76.

32. Askin R.G., Subramanian S.P. A cost-based heuristic for group technology configuration. Inter. Jour. Production Research, 1987, vol. 25, no. 1, pp. 101–113.

33. Stanfel L. Machine clustering for economic production. Engineering Costs and Production Economics, 1985, vol. 9, pp. 73–81.

34. McCormick W.T., Schweitzer P.J., White T.W. Problem decomposition and data reorganization by a clustering technique. Operations Research 1972, vol. 20, no. 5, pp. 993–1009.

35. Srinivasan G., Narendran T.T., Mahadevan B. An assignment model for the part-families problem in group technology. Intern. Jour. Production Research, 1990, vol. 28, no. 1, pp. 145–152.

36. King J.R. Machine-component grouping in production flow analysis: An approach using a rank order clustering algorithm. Intern. Jour. Production Research, 1980, vol. 18, no. 2, pp. 213–232.

37. Carrie S. Numerical taxonomy applied to group technology and plant layout. Intern. Jour. Production Research, 1973, vol. 11, pp. 399–416.

38. Mosier C.T., Taube L. Weighted similarity measure heuristics for the group technology machine clustering problem. OMEGA, 1985, vol. 13, no. 6, pp. 577–583.

39. Kumar K.R., Kusiak A., Vannelli A. Grouping of parts and components in flexible manufacturing systems. Europ. Jour. Operations Research, 1986, vol. 24, pp. 387–397.

40. Boe W., Cheng C.H. A close neighbor algorithm for designing cellular manufacturing systems. International Jour. Production Research, 1991, vol. 29, no. 10, pp. 2097–2116.

41. Chandrasekharan M.P., Rajagopalan R. (). Groupability: Analysis of the properties of binary data matrices for group technology. Intern. Jour. Production Research, 1989, vol. 27, no. 6, pp. 1035–1052.

42. Kumar K.R., Vannelli A. Strategic subcontracting for efficient disaggregated manufacturing. International Jour. Production Research, 1987, vol. 25, no. 12, pp. 1715–1728.

43. Chandrasekharan M.P., Rajagopalan R. ZODIAC: An algorithm for concurrent formation of part families and machine cells. Intern. Jour. Production Research, 1987, vol. 25, no. 6, pp. 835–850.