Историю развития сети Интернет можно уложить в несколько этапов, обладающих собственными Ежегодно проводимая противогриппозная вакцинация населения требует значительных затрат. В связи с этим большинство алгоритмов по оптимизации режима вакцинации исходит из экономических соображений. Однако не менее важной является медицинская сторона. Особенность ее учета состоит в том, что противогриппозная вакцинация сопровождается бессимптомной иммунизацией, вносящей свой вклад
в прирост коллективного иммунитета [1]. Той и другой свойственны как позитивный, так и негативный эффекты. Под позитивным эффектом понимается прирост числа лиц с нормальным уровнем иммунитета, а под негативным – прирост числа лиц с избыточным и недостаточным уровнем. Разные доли этих приростов (зависящие от скорости и длительности накопления лиц с разными уровнями иммунитета) приводят к необходимости найти такие параметры вакцинации, которые минимизируют негативные эффекты при заданном позитивном. Дело осложняется тем, что сезонная динамика возбудителя (от которой зависят эти эффекты) непостоянна, то есть в разные годы меняется по уровню и времени начала. Поэтому проведение вакцинации «плавает» в пределах трех осенних месяцев. Слишком раннее ее начало уменьшает долю естественного прироста коллективного иммунитета (за счет бессимптомных инфекций),
а слишком позднее уменьшает возможность достижения его нужного уровня (и к тому же грозит ростом клинически выраженных форм). Поэтому отыскание оптимального момента начала вакцинации важно и в экономическом, и в медицинском смыслах. В данной статье, в отличие от экономической направленности [2], описывается алгоритм оптимизации в медицинском смысле, причем, в отличие от алгоритма
с двойным режимом вакцинации и фиксированным моментом начала [3], строится алгоритм для однократной вакцинации с «плавающим» началом.

Система дифференциальных уравнений, описывающих изменение трех компонент коллективного иммунитета (нормальной, избыточной, недостаточной) при совместном действии вакцинной и естественной иммунизации имеет вид

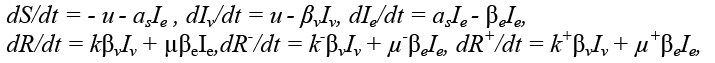
    (1)

где S – число лиц, восприимчивых к гриппу; Ie – число лиц, инфицированных естественно, Iv – искусственно (путем вакцинации); R-, R, R+ – соответственно прирост числа лиц с недостаточным уровнем антител, нормальным и избыточным; k-, k, k+ – доли приобретающих эти уровни искусственно, µ-, µ, µ+ – естественно (µ+ = 0); u – интенсивность вакцинации (число вакцинируемых за день); asIe – интенсивность естественной иммунизации (число естественно иммунизируемых за день); as – эмпирический коэффициент, определяемый числом восприимчивых и активностью возбудителя; βv = 1/Tv, βe = 1/Te, Tv и Te – характерные длительности поствакцинной и инаппарантной инфекции. Полагаем, что частота клинически выраженных форм инфекции крайне мала в этот период и ею можно пренебречь. Момент начала вакцинации (t = t*) будем отсчитывать от условно заданного начального момента времени (t = 0); в качестве такого момента избираем 1 октября. Пусть вакцинация должна заканчиваться к моменту времени
t = T [4].

Дополним систему (1) медицинским критерием качества, требуя суммарное число избыточных и недостаточных исходов иммунизации минимальным:

R-(T, u) + R+(T, u) → min, u ∊ U.                      (2)

В качестве ограничения потребуем достижение к моменту T нужного числа нормальных исходов совместной иммунизации:

R(T, u) = R*.                                                    (3)

Решение задачи (1)–(3) будем искать, используя принцип максимума Понтрягина  [5].

Составим гамильтониан:

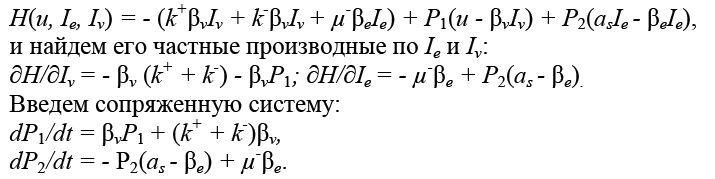
Начальные значения P1(0), P2(0) отыскиваются исходя из условий трансверсальности Pi(0)Pi(0) < 0
(i = 1, 2) и условия (3).

Представим нормальную компоненту коллективного иммунитета в виде суммы двух составляющих, из которых одна соответствует естественному (бессимптомному) вкладу, другая – вакцинному:

R(T) = Re(T) + Rv(T).

Так как задаваемая величина R* не должна превышать сумму этих двух компонент (R* ≤ Re(T) +
+ Rv(T)), необходимо дать оценки величинам Re(T), Rv(T).

При реальном соотношении βe = βv = β имеем:

 

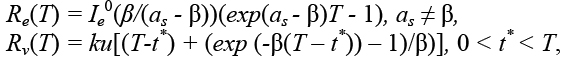
Для случая as - β < 0 получим:

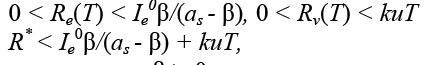          (4)

а для случая as – β > 0:

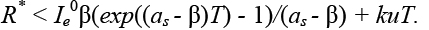    (5)

Настройка программы начинается с вычисления коэффициента as, определяемого числом восприимчивых и среднестатистической активностью возбудителя в начале сезона (сентябрь–октябрь). Так как рост активности протекает на спаде числа восприимчивых, то величина as в первом приближении может считаться постоянной. Ее находим из уравнения

∆Ie = (asIe - βIe) ∆t,

где ∆Ie – прирост числа естественно (бессимптомно) инфицированных за время ∆t = 1. Этот прирост соразмеряется с приростом заболеваемости в соотношении 1:1 [6]. Ежедневное наблюдение за суточной заболеваемостью и использование соотношения 1:1 между клиническими и бессимптомными исходами позволяет выделить тренд, необходимый для определения ∆Ie. В разные годы он может быть разным. Кроме того, и начальная величина Ie(0) может быть разной. Так как Ie(0) в значительной мере зависит от активности возбудителя [7], она определяется по результатам серологического мониторинга [1] с учетом особенностей данного места [8].

Начальные значения прочих переменных задаются следующим образом. Так как величины R-, R, R+ – приросты трех компонент коллективного иммунитета за время T, то их начальные значения берутся нулевыми:

R-(0) = 0, R(0) = 0, R+(0) = 0.

Также и Iv(0) = 0.

Коэффициенты распределения искусственно иммунизируемых лиц по трем уровням иммунитета
(k-, k, k+) определяются путем усреднения накопленных данных по различным исходам прививки, а коэффициенты распределения естественно иммунизируемых лиц (µ-, µ, µ+) – по результатам серологического мониторинга с помощью соотношения R- : R : R+ =  µ- : µ : µ+  и условия µ-+ µ+ µ+ = 1.

В информационную систему входят, помимо фазовых переменных, сопряженные переменные P1(t), P2(t). Область задания начального приближения к P1(0)P2(0) определяется положением точки равновесия сопряженной системы:

P1*= - (k+ + k-), P2* = µ-β/(as – β).

Независимо от знака разности (as – β) начальное приближение задается в области

P1* < P1 < 0; P2 < 0.

(что обусловлено неустойчивостью точки P*). Так как траектории из этой области, направляясь в первый квадрант, обязательно пересекают линию переключения P1=0, то найдется такая начальная точка P(0), которая при выполнении условий (4) и (5) обеспечит существование оптимального момента начала вакцинации t*.

Пример. Найдем оптимальный момент начала вакцинации для города с миллионным населением (H=1000 тыс. чел.) и среднестатистической осенней заболеваемостью 0,5 (тыс. чел./день). Пусть вакцинация должна заканчиваться 15 ноября, тогда T = 31 + 15 = 46 дней. Примем интенсивность вакцинации равной 5 тыс. чел./день, β = 0,1. Предположим, что серологический мониторинг дал Ie(0) = 150 тыс. чел., k = 0,4, k+ = 0,2, k- = 0,4, µ = 0,7, µ+ = 0, µ- = 0,3. Величина as находится из уравнения 0,5 = (as – 0,1)*150, откуда as  = 0,103. Пусть к моменту окончания вакцинопрофилактики (t = T) требуется получить прирост числа нормально иммунизированных равным 0,2 млн. чел. (200 тыс.) при минимальном негативном эффекте. Это означает, что при t = T должно выполняться R* = 200, R+(T) + R-(T) = min по всем t из интервала [0, T]. Результат вычислений показывает, что при заданных начальных условиях и требуемом R* оптимальным моментом начала вакцинации должен быть выбран 33-й день от 1 октября.

Предложенный алгоритм оптимизации направлен на снижение негативных последствий вакцинации, которые часто вызывают отказ от прививки. В этом отношении всякое предложение, уменьшающее число негативных последствий, имеет гуманный характер. Этой же целью руководствовались и авторы статьи [1]. Идеи этой статьи частично воплощены в предложенном алгоритме, входящем в информационную систему управления коллективным иммунитетом.

Литература

1. Медуницын Н.В., Яковлева Т.В. Совершенствование подходов к вакцинопрофилактике // Эпидемиология и вакцинопрофилактика. 2012. № 3. С. 70–78.
2. Hansen E. and Day T. Optimal control of epidemics with limited resources. J. Math. Biol., 2011, vol. 62, pp. 423–451.
3. Колесин И.Д., Житкова Е.М. Оптимизация противоэпидемической профилактики школьников // Автоматика и телемеханика. 2008. № 7. С. 129–135.
4. Колесин И.Д., Воробьева А.А., Циберная А.Ю. Модельный анализ эффективности ранней иммунизации населения // Эпидемиология и вакцинопрофилактика. 2015. № 5. С. 21–26.
5. Моисеев Н.Н. Математические задачи системного анализа. М.: Наука, 1981. 488 с.
6. Смородинцев А.А. Грипп и его профилактика. Л.: Медицина, 1984. 384 с.
7. Грипп: руководство для врачей; [под ред. Г.И. Карпухина]. СПб: Гиппократ, 2001. 356 с.
8. Kribs-Zaleta C.M. and Velasco-Hernandez J.X. A simple vaccination model with multiple endemic states, Math. Biosci. 2000, vol. 164, pp. 183–201.