При выполнении суперкомпьютерных расчетов используются различные расчетные сетки. В блочно-структурированных расчетных сетках [1] ячейки объединяются в блоки, представляющие собой трехмерные массивы, внутри которых обращение к ячейкам осуществляется по индексам. Это значительно ускоряет работу по сравнению с неструктурированной сеткой, однако сильно усложняет построение. Каждый блок сетки, как правило, целиком обрабатывается на отдельном вычислителе, а обмен данными между блоками выполняется с использованием MPI [2]. Для выполнения расчетов на неструктурированных сетках [3] вначале требуется разбить сетку на домены, каждый из которых впоследствии будет отнесен к конкретному вычислителю.

В настоящее время существует достаточно много алгоритмов декомпозиции неструктурированных расчетных сеток. Среди них можно указать линейное распределение ячеек по доменам (без учета геометрии и связей) [4], методы координатной и инерциальной бисекций [4, 5], разбиение с использованием кривой Гильберта [6], алгоритмы с использованием локального уточнения [7], множество иерархических алгоритмов разбиения [8], алгоритмы наращивания доменов [9].

При распределении частей расчетной задачи (блоков блочно-структурированной сетки или доменов неструктурированной сетки) между вычислителями суперкомпьютерного кластера важно учитывать характеристики самого кластера, к которым относятся производительность вычислителей и скорость обмена данными между ними. Стоит также отметить, что в один кластер могут входить вычислители с разными архитектурами [10], а соотношение между их характеристиками могут зависеть от конкретной решаемой задачи, что осложняет разработку единого универсального алгоритма распределения вычислительной нагрузки. В данной статье приводится описание эвристического алгоритма распределения вычислительной нагрузки на вычислительный кластер с учетом геометрии расчетной задачи и характеристик кластера. При разработке данного алгоритма основной целью ставилось повышение эффективности запусков расчетных задач газовой динамики на гетерогенном суперкомпьютере МВС-10П [11], находящемся в МСЦ РАН.

Постановка задачи

Введем понятие графа вычислительного кластера H =( V_H, E_H). Узлы данного графа соответствуют отдельным вычислителям кластера (одному процессору или сопроцессору), а ребра – логическим соединениям между вычислителями (то есть возможен обмен данными). Так как между любыми двумя вычислителями возможен обмен данными, граф H является полным (и даже псевдографом, так как содержит все возможные петли). Введем на данном графе две весовые функции. Первая функция 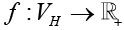 каждому узлу графа ставит в соответствие скорость работы соответствующего вычислителя, то есть количество расчетных данных, которые могут быть обработаны на нем за одну условную единицу времени (для разных вычислительных задач функции могут различаться). Вторая функция  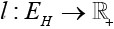несет смысл скорости обмена данными между вычислителями, она показывает количество данных, которые могут быть переданы между соответствующими вычислителями за одну условную единицу времени.

Также будем рассматривать граф задачи G = ( V_G, E_G), который отражает особенности декомпозиции расчетной области (это может быть граф блочно-структурированной расчетной сетки или граф доменов неструктурированной сетки). Узлы данного графа соответствуют компактно расположенным в пространстве множествам данных, каждое из которых обрабатывается одним вычислителем. Ребра графа соответствуют потокам данных между разными частями задачи. На данном графе также вводятся две весовые функции. Первая функция 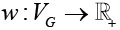 имеет значение объема вычислительных данных, обрабатываемых в соответствующей части задачи. Вторая функция  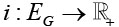отражает объем данных, пересылаемых между частями задачи при межпроцессном обмене. Значения всех четырех функций (f, l, w, i) измеряются в одних и тех же единицах (это могут быть ячейки расчетной сетки, количество байтов или вещественных значений).

Расчет задачи состоит из двух чередующихся фаз: проведение итерации расчета и выполнение межпроцессных обменов данными. Будем считать, что эти фазы не перемешиваются для отдельных частей задачи (хотя можно выполнять расчеты для одной части задачи и одновременно проводить межпроцес-сные обмены для другой ее части). Требуется таким образом распределить задачу между вычислителями кластера, чтобы суммарное время одной итерации расчета и одной итерации межпроцессных обменов было минимальным. Распределение задачи между вычислителями кластера определяется функцией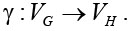

Время выполнения одной итерации вычислений определяется по самому загруженному вычислителю:

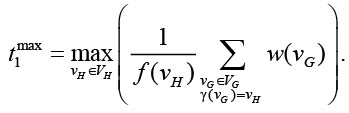
Аналогично время выполнения одной итерации межпроцессных обменов определяется по самому загруженному каналу обмена:

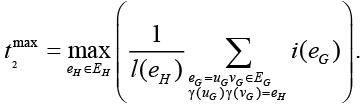
Таким образом, задача поиска оптимального распределения задачи по вычислителям кластера сводится к поиску функции 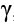, минимизирующей значение функционала 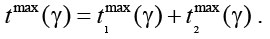Так как каждый элемент из множества V_G может быть отнесен к любому вычислителю, общее количество всех функций распределения равно .

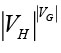Можно рассматривать частные случае задачи распределения вычислительной нагрузки. Для вычислительных задач с малой долей межпроцессных обменов можно ограничиться минимизацией функционала 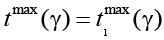. Также можно рассматривать задачу распределения для гомогенного кластера, для которого функции f и l являются константами. Минимизируемый функционал в этом случает принимает следующий вид:

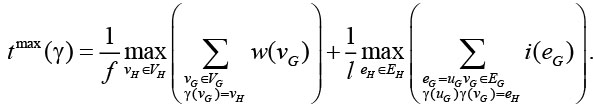
На сегодняшний день нет информации о существовании эффективных алгоритмов поиска точного решения поставленной задачи. В данной статье приводится описание эвристического алгоритма поиска приближенного решения, который учитывает весовые функции графов задачи и вычислительного кластера, а также геометрию расчетной области задачи.

Описание алгоритма

Одной из особенностей вычислительного кластера является то, что скорость обмена данными между двумя частями задачи, обрабатываемыми одним вычислителем, существенно выше, чем скорость обмена данными между двумя частями задачи, обрабатываемыми двумя разными вычислителями. Интуитивно понятно, что задача должна распределяться между узлами вычислительного кластера таким образом, чтобы расположенные рядом части задачи попадали на один вычислитель. В идеале граф G задачи должен быть разбит на |V_H| связных партиций, каждая из которых обрабатывается своим вычислителем, причем вес партиции (суммарный вес частей задачи, входящих в партицию) должен быть пропорционален весу соответствующего вычислителя.

Каждому узлу графа G поставлена в соответствие точка трехмерного пространства (центр соответствующей части расчетной задачи). С использованием данных точек формировать партиции можно по геометрическому принципу. Для этого сначала нужно выполнить первую фазу алгоритма – определить базовые точки, вокруг которых в дальнейшем будут формироваться партиции. Базовые точки должны быть распределены по объему расчетной области задачи таким образом, чтобы веса сформированных впоследствии партиций были пропорциональны весам вычислителей. Будем считать, что все ячейки расчетной сетки, используемой в задаче, имеют примерно равные размеры. Это означает, что нет заметных сгущений и разряжений сетки. В противном случае нужно добавлять дополнительные корректирующие коэффициенты, что выходит за рамки данной статьи. В условии нашего допущения объем области, занимаемой партицией, будет пропорционален ее весу. Таким образом, задача определения базовых точек сводится к следующему: требуется в данной области пространства определить такое множество точек, чтобы объемы окрестностей, окружающих эти точки, были пропорциональны весам вершин графа H. При этом окрестность точки строго не определяется. Главное, чтобы окрестность содержала саму точку и имела интуитивно компактную форму.

Добиться определения базовых точек можно с помощью простого итерационного алгоритма с имитацией взаимного отталкивания точек друг от друга. Обозначим область расчетной задачи через Ω. На первом шаге расположим | V_H| точек (будем обозначать их с помощью соответствующих радиус-векторов) случайным образом внутри области Ω. Каждой базовой точке поставим в соответствие конкретную вершину графа H. Таким образом, каждая точка 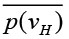 будет иметь вес f(v_H). Далее на каждом шаге будем моделировать силу взаимного отталкивания между двумя точками 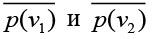по закону

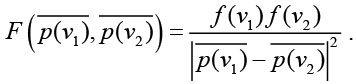
После этого будем корректировать положение каждой точки под действием суммарной силы отталкивания от всех остальных точек. Кроме того, суммарную силу нужно дополнить корректирующей силой отталкивания от границ области Ω, иначе все точки будут располагаться на этой границе. Алгоритм заканчивает свою работу, когда положение точек стабилизируется, что говорит об уравнивании всех моделируемых сил отталкивания.

На рисунке 1 проиллюстрирована работа алгоритма определения базовых точек внутри квадратной области в двумерном случае. На рисунке слева все точки имеют одинаковые веса, на рисунке справа выделены три точки, имеющие случайные веса, значительно превышающие среднее значение.

После определения базовых точек можно переходить ко второй фазе алгоритма – определение (наращивание) партиций вокруг базовых точек. На каждом шаге наращивания партиций будем выбирать партицию с минимальным значением:

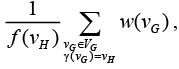
характеризующим время обработки данных этой партиции на одной итерации расчетов, и добавлять к ней новую вершину из V_G. Если на текущем шаге рассматриваемая партиция пуста, то добавим к ней вершину из V_G, расположенную ближе всех к базовой точке p(v_H). Если рассматриваемая партиция уже содержит точки, то рассмотрим ее окрестность. Окрестностью партиции 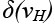назовем множество не входящих в нее (и ни в какую другую партицию) вершин графа G, соединенных ребром хотя бы с одной вершиной из этой партиции. Выберем из данной окрестности вершину v с максимальным показателем предпочтения q(v), который определяется по следующей формуле:

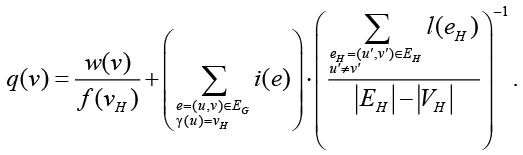
Первое слагаемое в данной формуле отражает скорость обработки данных из части задачи, соответствующей вершине v, на вычислителе v_H. Второе слагаемое отражает время межпроцессных обменов, которое удастся сократить после добавления в партицию вершины v (при этом в качестве скорости обменов берется среднее значение функции l по всем вершинам графа H, кроме петель).

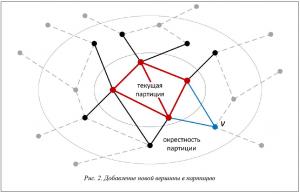
На рисунке 2 показано расширение текущей партиции (отмечено красным) за счет добавления новой вершины (v). При этом ребра, отмеченные синим цветом, становятся внутренними ребрами партиции, что гарантирует ускорение обмена данными по этим ребрам.

Так как количество вершин в графе G конечно, а на каждом шаге алгоритма в некоторую партицию добавляется одна вершина, алгоритм заканчивает свою работу, когда все вершины распределены по партициям.

На шаге расширения партиции возможна такая ситуация, когда вся окрестность текущей партиции уже распределена по соседним партициям. Такое возможно на последних шагах распределения, когда остается малое количество нераспределенных частей задачи. В этом случае партицию можно расширить просто ближайшей свободной вершиной графа G. Это приводит к тому, что в распределении оказываются отдельные вершины графа G, принадлежащие одной партиции, полностью окруженные вершинами из других партиций. Для корректировки таких неэффективных с точки зрения обмена данными аномалий выполняется третья фаза алгоритма – захват партициями внутренних точек, на этой фазе партиция может поглотить небольшие анклавы вершин графа G.

Результаты работы

Для анализа эффективности описанного алгоритма рассматривалась модельная задача, двумерная квадратная расчетная область которой равномерно разбита на близкие по размеру части. В качестве расчетного кластера рассматривались гомогенный и гетерогенный кластеры, содержащие 8 вычислителей.

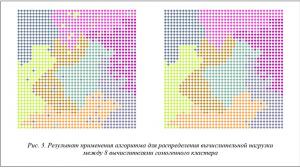
На рисунке 3 проиллюстрирована работа алгоритма распределения вычислительной нагрузки для модельной задачи между 8 вычислителями гомогенного кластера (то есть все вычислители идентичны). Слева представлены результаты после второй фазы алгоритма, при этом наблюдается некоторое перемешивание партиций. Справа показаны результаты после третьей фазы алгоритма, на которой корректируется связность партиций путем поглощения отдельных узлов графа G, попавших не в свою партицию.

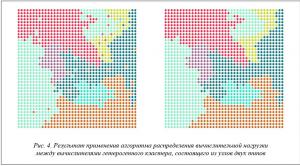
На рисунке 4 показаны аналогичные результаты работы алгоритма для гетерогенного кластера, состоящего из узлов двух типов, отличающихся по производительности друг от друга в 4 раза. На иллюстрациях видна разница в размерах партиций, отнесенных к тому или иному типу вычислителя.

Из рисунков 3 и 4 видно, что получившиеся партиции имеют довольно протяженные изломанные границы, что негативно влияет на скорость межпроцессных обменов. Для их сокращения требуется проведение дополнительной фазы алгоритма, состоящей в выравнивании границ (например, с помощью диффузионного перераспределения [10]).

Для оценки эффективности алгоритма, кроме характеристики времени исполнения одной вычислительной итерации и одной итерации межпроцессных обменов

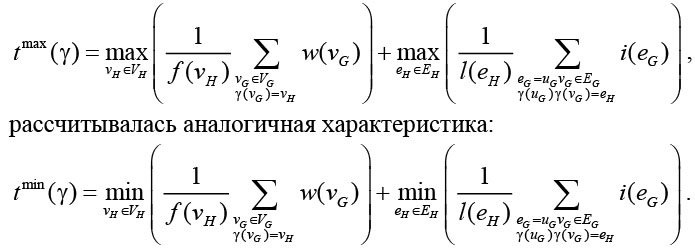
Разность этих двух значений отражает неэффективность распределения, связанную с простоем вычислительных ресурсов.

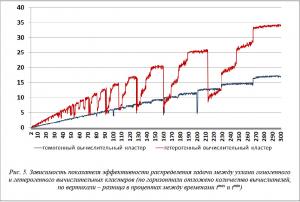
Для модельной задачи были проведены эксперименты по распределению графа задачи на узлы гомогенного и гетерогенного кластеров при изменении количества вычислителей от 2 до 300. На рисунке 5 представлены полученные зависимости. Видно, что для обоих видов кластеров при увеличении количества вычислителей наблюдается линейная тенденция к снижению эффективности распределения, но в случае гетерогенного кластера эффективность распределения ниже и зависимость от количества узлов в этом случае более сложная.

Заключение

Разработан алгоритм распределения вычислительной нагрузки между вычислителями суперкомпьютерного кластера, в котором учитываются характеристики не только отдельных частей расчетной задачи, но и самого кластера (производительность вычислителей, конфигурация связей между ними, скорость обменов между отдельными вычислителями, что в совокупности можно охарактеризовать как топологию кластера). Приведены результаты работы предложенного алгоритма на модельной задаче, показана зависимость эффективности распределения при увеличении количества вычислителей кластера (масштабируемость в сильном смысле). Анализ результатов работы алгоритма показывает, что использование данного подхода имеет практическую значимость, однако требуется добавление в алгоритм дополнительной фазы, направленной на сглаживания границ образующихся партиций.

Работа выполнена в МСЦ РАН в рамках проведения фундаментальных научных исследований по теме «Разработка архитектур, системных решений и методов для создания вычислительных комплексов и распределенных сред мультипетафлопсного диапазона производительности, в том числе нетрадиционных архитектур микропроцессоров».

Литература

1. Farrashhalvat M., Miles J.P. Basic structured grid generation: With an introduction to unstructured grid generation. Butterworth-Heinemann Publ., 2003, 256 р.

2. Queen M. Parallel programming in C with MPI and OpenMP. Mc-Grow Hill Publ., 2004, 529 р.

3. Liseikin V. Grid generation methods. Springer, 2010, 541 p.

4. Hendrickson B., Leland R. The Chaco user's guide. Version 2.0. Technical Report, SAND95-2344, Sandia National Lab., Albuquerque, NM, 1995, 44 p.

5. Якобовский М.В. Введение в параллельные методы решения задач. М.: Изд-во МГУ, 2013. 328 с.

6. Schamberger S., Wierum J.M. A locality preserving graph ordering approach for implicit partitioning: Graph-filling curves. Proc. 17th Intern. Conf. on Parallel and Distributed Computing Systems (PDCS 2004), ISCA Publ., 2004, pp. 51–57.

7. Kernighan B.W., Lin S. An efficient heuristic procedure for partitioning graphs. Bell Syst. Tech. Jour., 1970, pp. 291–307.

8. Karypis G., Kumar V. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J. Sci. Comp., 1998, vol. 20, no. 1, pp. 359–392.

9. Farhat C. A simple and efficient automatic fem domain decomposer. Computers & Structures, 1988,
vol. 5, iss. 28, pp. 579–602.

10. Дикарев Н.И., Шабанов Б.М. Архитектура высокопроизводительных вычислительных систем. М.: ФАЗИС, 2015. 108 с.

11. Описание интерфейса пользователя, предназначенного для работы с интеловской гибридной архитектурой суперЭВМ (СК), где вместе с процессорами Intel Xeon используются сопроцессоры Intel Xeon Phi. URL: http://www.jscc.ru/informat/MVS-10PInter.pdf (дата обращения 011.01.2018).

12. Якобовский М.В. Инкрементальный алгоритм декомпозиции графов // Вестн. Нижегородского ун-та им. Н.И. Лобачевского: Математическое моделирование и оптимальное управление. 2005. Вып. 1.
С. 243–250.