Technical condition (TC) control implies the process of collecting and processing information in order to predict events [1, 3, 6]. In aircraft (AC) control practice the stage of measurement data processing in order to obtain conclusions about (TC) of the object under control is considered as ТС analysis. It is possible
to distinguish the following tasks among the current tasks of analysis:

• Analysis of the planned modes performance for the object as a whole
• Analysis of full-time systems performance
• Analysis of support systems mechanization performance and the process of dynamic operations
• Analysis of applied equipment mechanization performance
• Calculation of full-time systems characteristics
• Analysis of dynamic processes
• Analysis of applied measurements

Problem Statement

Let us state the problem of AC ТС operating control with the use of fuzzy measurement. At the same time let us agree that in order to make a decision regarding TC, a priori and a posteriori data must be formalized in a single and united way, i.e. with the use of fuzzy measurement. Then, based on a preliminary analysis, let a set of classes of technical condition of objects under control be given F = {F_r} (r = 1, 2, …, n) in the form of fuzzy sets 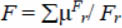 with the corresponding membership functions  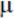^F_r.

ТС of the object under control is evaluated according to implementations of particular condition parameters – characteristics of control that form in the aggregate the set of control characteristics Х = {Х _i} (i = 1. 2, …, m). Moreover, taking specific character of the object under control into consideration – remotely controlled aircraft – information about the object's condition will be received from the data measuring system in the form of telemetered data set (TMD). Then, evaluation of every of the Х _i* characteristics will be formed based on appropriate processing of TMD results.

Sets of TC F classes and Х control characteristics are in certain interrelations 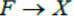 that can be described with the help of a control matrix with elements {F_r, Х _i}, i.e. every ТС is mapped to the corresponding implementation of control characteristics.

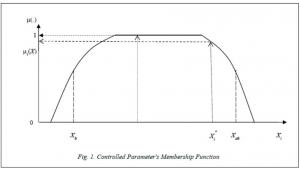
Reliability indicators of control characteristics evaluation Х_i* were set in the form of the corresponding membership functions 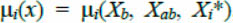, where Х_ab, Х_b - are upper and lower threshold limit values of the controlled character, Х_i* - is its evaluation, obtained as a result of TMD processing (fig. 1).

Criterion and reliability indicator are known to resolve the problem of ТС control in the form of 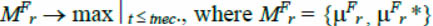 is a generalized membership function of the r-s technical condition obtained by way of composition of the a priori  membership functions of r-s technical condition; t and t_nec are indicator and criterion of operational control, acting as restrictions.

To solve the stated problem it is necessary to develop the method for evaluation of a posteriori reliability 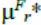 of ТС control results, expressed to a fuzzy extent. Then the general solution of the control problem in accordance with the given statement of the problem can be found in the form of F_r* = arg max М^F _r.

Method to Solve the Problem

Developing the method to resolve the problem, let us use the methods of condition search tree and conditions matrix [2,7].

The algorithm for analysis of AC systems performance that uses the method of condition search trees,
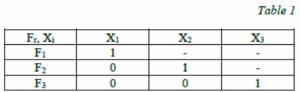
is based on sequential analysis of reliable and important values of controlled parameters {X_i} (i = 1, 2, …, n) of AC systems and (or) of results of intermediate calculations performed on X_i* actual values. The analysis consists in comparing each value with known threshold values X_ith, for example, Х_in < Х_i* < X_ib. or X _iab< Х_i*; Х_i * > X_ith, and concluding "parameter Х_i is normal (abnormal)". Searching for AC system current condition branches forth depending on step by step results of this analysis and ends up with the F_r definition of onboard AC system condition after a couple of steps of such sequential analysis. The control matrix in the method of condition tree search can, for example, look the following way (table 1):

In the table it is assumed that "1" – indicates that the Х_i parameter is normal; "0" - correspondingly, " Х_i parameter is abnormal"; "-" - the present parameter is not controlled at this step.

The result of technical condition analysis using the algorithm of condition search trees can be interpreted as the event {F*} consisting in identification of the AC system current condition to a specific type of technical condition F_r. The event {F_r} occurs if and only if k events occur that are the results of sequential analysis operations along the corresponding branch of the algorithm, for example,

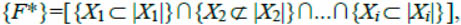                           (1)

where 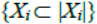 - is the event that the value of the parameterХ_i is normal;  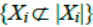- is the event that the value of the parameter Х_i is abnormal. Reliability of such an event is determined by the logical conjunction of reliability of individual events and is expressed either as “1” or “0”, which in practice is an unjustified idealization.

Using the fuzzy measure of reliability allows obtaining quantitative reliability estimation, reflecting the real degree of proximity to the estimation of the true TC. The intersection of events in the theory of fuzzy sets [5,8] corresponds to the min operation and according to (1), reliability of TC analysis results to a fuzzy extent, as the degree of truth of the statement "according to the results of measurements, the current TC refers to the F_r class of TC" can be represented as follows:

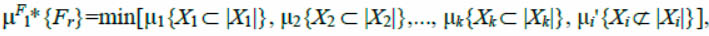                 (2)

where 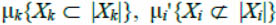 - are values of membership functions characterizing the degree of truth of the statement "Х_k parameter is normal" or "Х_i parameter is above (Х _iab) or below (Х_ib) the norm" accordingly.

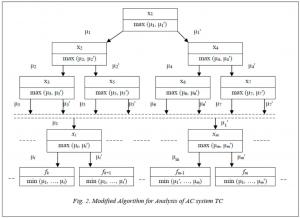
The choice of corresponding modified algorithm branch of the condition search tree is carried out by the operation of comparison of μ _i with μ_i'. The branch is selected that corresponds to the larger value of the membership function max (μ _i, μ_i') and the choice rule taking into account the expression (2) can be represented as follows:

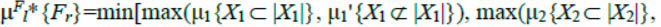                 (3)

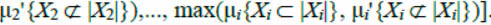
Modified algorithm of AC system TC analysis that uses the method of condition search trees is shown in the Figure 2.

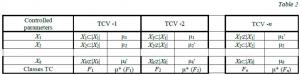
Algorithms for AC systems performance analysis that are based on condition matrices [9,10] use the fact that F_r condition of a system can be determined by a set of Х_i values of controlled parameters. Groups of functionally and logically interconnected parameters reflecting, in combination, possible conditions of AC device or system, form technical condition vectors (TCV). Every TCV describes one of possible technical conditions of the AC system, F_r, and forms a row of condition matrix. Moreover, controlled parameters Х _i are subject to tolerance control and in fact TCV parameters are events "Х_i parameter is normal (abnormal)" with reliability "1" or "0". Using fuzzy measure of reliability every value of the measured parameter Х_i corresponds to a particular value of the membership function μ_i(Х _i) characterizing the degree of truth of the statement "Х_i parameter is normal", "Х _i parameter is above (below) the norm". In this case conditions matrix can be represented as in Table 2.

Reliability of ТС analysis result obtained using the method of conditions matrix to a fuzzy extent, as shown above, will be determined with the expression (2) as reliability of events intersection.

Consequently, according to analysis results either the method of condition search "tree", or the method
of condition matrices form a posteriori set of classes of the controlled object technical condition F = {F_r}(r = 1, 2, …, n) in the form of the fuzzy set 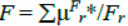 according to a posteriori membership functions μ^F _r*.

The final decision will be made by calculating the generalized membership function of the r-s ТС in the form of F_r* = arg max М^F_r by one of composition variants of a priori m^F_r and a posteriori μ^F_r* membership functions, for example, from the optimistic perspective М^F_r = max{μ^F_r, μ^F_r*}, from the pessimistic perspective М ^F _r = min{μ^F_r, μ^F_r*} or from the objectivist's standpoint М^F_r = μ^F_r · μ^F _r* [4].

Conclusion

The above discussed modifications to methods of ТС analysis allow evaluating a posteriori reliability μ^F _r* of control results, expressed as fuzzy measurement, and can be used as the basis for the synthesis
of modified algorithms for automated analysis of TC of onboard AC systems. Advantage of the methods
is the ability to obtain a quantitative assessment of reliability of each of the given TC. Practical implementation of the methods is possible through a certain refinement of the corresponding mathematical support and software.

Acknowledgements. The study was doneas part of national assignment for SRISA RAS (fundamental scientific research GP 14) on the topic No.0065-2019-0001 (АААА-А19-119011790077-1).

References

1. Klyuev V.V., Parkhomenko P.P., Abramchuk V.Yе., et al. Diagnostic Tools. Moscow, Mashinostroenie Publ., 1989, 671 p. (in Russ.)

2. Kravets V.G. Automated space flight control systems. Moscow, Mashinostroenie Publ., 1995. 256 p.

3. Potyupkin А.Yu. The use of fuzzy measures in the tasks of monitoring the technical condition of aircraft. Measurement Techniques, 2002, no. 7, pp. 12–16.

4. Pospelov D.А. (Ed.). Fuzzy sets in control and artificial intelligence models. Moscow, Nauka Publ., 1986, 312 p.

5. Genov A.A., Rusakov K.D., Hill S.Sh. Identification of a complex technical system functional state under conditions of measurement data ambiguity. Programmnye produkty i sistemy [Software & Systems] . 2017, vol. 30, no. 3, pp. 373–377 (in Russ.). DOI: 10.15827/0236-235X.119.373-377.

6. Dmitriev А.К., Mal'tsev P.А. Fundamentals of the theory of construction and control of complex systems . Leningrad, Energoatomizdat Publ., 1988. 192с.

7. Rusakov К.D., Khil' S.Sh. On the problem of selecting signs of the observed state of a complex dynamic object in conditions of different quality of measurement information.Proc. XV All-Russian Sci. Conf. Neurocomputers and their application, Moscow, 2017, pp. 246–248.

8. Kirillov N.P. The functional state of the technical object. Definition of a concept. J. Aerospace Instrument-Making, 2010, no. 10, pp. 31–40.

9. Rusakov К.D. To the assessment of the functional state of RCT objects in conditions of various quality of measurement information.Proc. XV All-Russian Sci. Conf. Neurocomputers and their application, Moscow, 2016, pp. 89.

 

ПРИМЕНЕНИЕ НЕЧЕТКОЙ МЕРЫ ДОСТОВЕРНОСТИ ДЛЯ АНАЛИЗА ТЕХНИЧЕСКОГО СОСТОЯНИЯ ЛЕТАТЕЛЬНЫХ АППАРАТОВ В УСЛОВИЯХ НЕСТОХАСТИЧЕСКОЙ НЕОПРЕДЕЛЕННОСТИ

 

С.Ш. Хиль ¹ , к.т.н, доцент, skhill@mail.ru

В.Н. Решетников ² , д.ф-м.н, профессор, главный научный сотрудник, rvn_@mail.ru

С.Б. Савилкин ² , к.ф-м.н, доцент, старший научный сотрудник, Savilkin@mail.ru

 

¹ Московский авиационный институт (Национальный исследовательский университет), Москва, Волоколамское ш., 4

² Центр визуализации и спутниковых информационных технологий, ФНЦ НИИ Системных исследований РАН, Москва, Нахимовский пр-т, 36

В связи с повышением уровня сложности летательных аппаратов и ужесточением требований по оперативности контроля технического состояния остро стоит вопрос автоматизации решения задач анализа. Отдельные результаты были получены, например, при разработке унифицированных алгоритмов автоматизированного анализа телеметрической информации, поступающей с борта пилотируемых космических аппаратов. Основой алгоритмов явилась совокупность методов контроля, в частности, метода многоуровневого контроля, деревьев поиска состояний, матриц состояний и др. С их помощью удается выполнить оперативный анализ технического состояния большинства систем летательных аппаратов, однако существенным недостатком при этом является невозможность количественной оценки достоверности заключений о техническом состоянии систем.

Рекомендуемая ГОСТ 19919 – 74 вероятностная мера достоверности в практике управления летательными аппаратами применяется ограниченно из-за отсутствия достаточной статистики, а также ресурсных и временных ограничений. В связи с этим задача разработки методов контроля технического состояния летательных аппаратов, позволяющих получать оперативные заключения о техническом состоянии контролируемого объекта с количественной оценкой достоверности в условиях нестохастической неопределенности, является актуальной. Возможным вариантом ее решения является использование нечеткой меры достоверности.

Важной составляющей современной системы управления летательными аппаратами различного назначения является подсистема контроля технического состояния. При этом под контролем понимается процесс сбора и обработки информации с целью определения событий. В практике управления летательными аппаратами этап обработки измерительной информации с целью получения заключения о техническом состоянии объекта контроля рассматривается как анализ технического состояния.

В статье рассмотрены модификации известных методов автоматизированного анализа технического состояния бортовых систем летательных аппаратов различного назначения, основанные на применении нечеткой меры достоверности.

Ключевые слова : система управления летательным аппаратом, техническое состояние, мера достоверности, стохастическая неопределенность.

 

Благодарности. Исследование проведено в рамках государственного задания ФГУ ФНЦ НИИСИ РАН (выполнение фундаментальных научных исследований ГП 14) по теме № 0065-2019-0001 "Математическое обеспечение и инструментальные средства для моделирования, проектирования и разработки эле-ментов сложных технических систем, программных комплексов и телекоммуникационных сетей в различных проблемно-ориентированных областях" (АААА-А19-119011790077-1).

Литература

1. Клюев В.В., Пархоменко П.П., Абрамчук В.Е. [и др.]. Технические средства диагностирования. М.: Машиностроение, 1989. 671 с.

2. Кравец В.Г. Автоматизированные системы управления космическими полетами. М.: Машиностроение, 1995. 256 с.

3. Потюпкин А.Ю. Применение нечеткой меры в задачах контроля технического состояния летательных аппаратов // Измерительная техника. 2002. № 7. С. 12–16.

4. Нечеткие множества в моделях управления и искусственного интеллекта; [под ред. Д.А. Поспелова]. М.: Наука, 1986. 312 с.

5. Генов А.А., Русаков К.Д., Хиль С.Ш. Идентификация состояния сложной технической системы в условиях неопределенности измерительной информации // Программные продукты и системы. 2017. Т. 30. No 3. С. 373–377. DOI: 10.15827/0236-235X.119.373-377.

6. Дмитриев А.К., Мальцев П.А. Основы теории построения и контроля сложных систем. Л.: Энергоатомиздат, 1988. 192с.

7. Русаков К.Д., Хиль С.Ш. О задаче выбора признаков наблюдаемого состояния сложного динамического объекта в условиях различного качества измерительной информации // Нейрокомпьютеры и их применение: сб. тр. XV Всерос. науч. конф. М., 2017. С. 246–248.

8. Кириллов Н.П. Функциональное состояние технического объекта. Дефиниция понятия // Авиакосмическое приборостроение. 2010. №10. С. 31–40.

9. Русаков К.Д. К оценке функционального состояния объектов РКТ в условиях различного качества измерительной информации // Нейрокомпьютеры и их применение: сб. тр. XIV Всерос. науч. конф. М.: МГППУ, 2016. С. 89.