Метод роя частиц (Particle Swarm Optimization, PSO) является методом стохастической оптимизации, в чем-то схожим с эволюционными алгоритмами. Этот метод моделирует не эволюцию, а ройное и стайное поведение животных [1]. В отличие от популяционных методов PSO работает с одной статической популяцией, члены которой постепенно улучшаются с появлением информации о пространстве поиска. Данный метод представляет собой вид направленной мутации (directed mutation). Решения в PSO мутируют в направлении наилучших найденных решений. Частицы никогда не умирают (так как нет селекции).
Рассмотрим каноническую парадигму метода PSO, разработанную Джеймсом Кеннеди и Расселом Эберхартом [2]. Метод PSO работает в многомерных, вещественных, метрических пространствах. Многомерное пространство поиска населяется роем частиц [3]. Каждая частица представляет некоторое решение. Основу поведения роя P = {pi|i = 1, 2, …, n} частиц составляет самоорганизация, обеспечивающая достижение общих целей роя на основе низкоуровневого взаимодействия. Каждая частица pi размещается в позиции xi многомерного пространства поиска, связана и может взаимодействовать со всеми частицами роя и тяготеет к лучшему решению роя. Процесс поиска решений итерационный. На каждой итерации вычисляется приспособленность частиц и при необходимости обновляется информация о наилучших найденных позициях.
По аналогии с эволюционными стратегиями рой частиц можно трактовать как популяцию, а частицу как индивида (хромосому). Это дает возможность построения гибридной структуры поиска решения, основанной на сочетании генетического поиска с методами роя частиц [4]. В гибридных алгоритмах преимущества одного алгоритма могут компенсировать недостатки другого. Связующим звеном такого подхода является структура данных, описывающая в виде хромосомы решение задачи [5]. Положение частицы в пространстве поиска является эквивалентом генотипа в эволюционных алгоритмах. Если в качестве частицы используется хромосома, то число параметров, определяющих положение частицы в пространстве решений, должно быть равно числу генов в хромосоме. Значение каждого гена откладывается на соответствующей оси пространства решений. В этом случае возникают некоторые требования к структуре хромосомы, значениям генов и пространству поиска.
В работе предлагается подход к построению модифицированной парадигмы роя частиц, обеспечивающей возможность одновременного использования хромосом с целочисленными значениями параметров в генетическом алгоритме и в алгоритме на основе роя частиц. Предлагается композитная архитектура многоагентной системы бионического поиска на основе роевого интеллекта и генетической эволюции [6]. Первый и наиболее простой подход к гибридизации заключается в следующем. Сначала поиск решения осуществляется генетическим алгоритмом [7]. Затем на основе популяции, полученной на последней итерации генетического поиска, формируется популяция для роевого алгоритма. В формируемую популяцию включаются лучшие, но отличные друг от друга хромосомы. При необходимости полученная популяция доукомплектовывается новыми индивидами. После этого дальнейший поиск решения осуществляется роевым алгоритмом.
При втором подходе метод роя частиц используется в процессе генетического поиска и играет роль, аналогичную генетическим операторам. В этом случае на каждой итерации генетического алгоритма синтез новых хромосом осуществляется с помощью, с одной стороны, кроссинговера и мутации, а с другой, операторов направленной мутации метода роя частиц.
Каноническая парадигма роя частиц предусматривает использование вещественных значений параметров в многомерных, вещественных, метрических пространствах. Однако в большинстве генетических алгоритмов гены в хромосомах имеют целочисленные значения. В свою очередь, хромосомы являются некоторыми интерпретациями решений, которые трансформируются в решения путем декодирования хромосом.
Анализ существующих методов и алгоритмов показал, что в качестве структуры данных, несущих информацию о решении, чаще всего используются списки, фактически являющиеся интерпретациями решений.
Данное представление удобно для его использования в различных метаэвристиках (генетические алгоритмы, муравьиные алгоритмы).
На списки, используемые в качестве интерпретаций решений, в зависимости от специфики задачи накладываются ограничения.
В отличие от канонической парадигмы роя частиц гибридные алгоритмы для представления решений используют широкий диапазон графовых структур (маршрут, дерево, двудольный граф, паросочетание, внутренне устойчивое множество) [8–11]. Такой подход является эффективным способом поиска рациональных решений для задач оптимизации, допускающих интерпретацию решений в виде различного рода графовых структур.
Это не позволяет напрямую использовать каноническую парадигму (например, задача направленной мутации одного дерева в направлении другого с формальной точки зрения является весьма нетривиальной).
В связи с этим актуальна разработка модернизированной структуры пространства поиска, структуры данных для представления решений и позиций, модернизированных механизмов перемещения частиц в пространстве поиска. Исследования показали, что структуры данных для представления позиций и механизмы перемещения частиц в пространстве поиска связаны, но зависят от структуры данных для представления интерпретаций решений. В работе рассматриваются древовидные представления решений. Решения представляется в виде хромосом, используемых без трансформаций как в роевом, так и в генетическом алгоритмах.
Структуры хромосом для древовидных представлений решений
Введем алфавит A = {O, •}. Структуру дерева разрезов можно задать, используя на базе алфавита A польское выражение для бинарного дерева, где знак O соответствует листьям дерева разрезов (областям), а знак • – внутренним вершинам дерева (разрезам). Польские выражения для деревьев, представленных на рисунке 1, имеют вид: OO•OOO•••, OO OO ••O•.
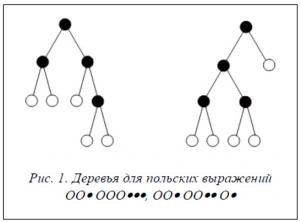 Процесс восстановления дерева по польскому выражению достаточно прост. Последовательно слева направо просматривается польское выражение, и отыскиваются буквы типа •, соответствующие разрезам. Каждый такой разрез объединяет два ближайших образованных на предыдущих шагах подграфа, расположенных в польской записи слева от знака •.
Процесс восстановления дерева по польскому выражению достаточно прост. Последовательно слева направо просматривается польское выражение, и отыскиваются буквы типа •, соответствующие разрезам. Каждый такой разрез объединяет два ближайших образованных на предыдущих шагах подграфа, расположенных в польской записи слева от знака •.
Отметим основные свойства польского выражения, выполнение которых необходимо, чтобы выражению соответствовало дерево разрезов. Обозначим через nx число элементов польского выражения типа O, а через n• – число элементов типа •. Для дерева разрезов всегда выполняется равенство nx = n· + 1.
Если в польском выражении провести справа от знака · сечение, то слева от сечения число знаков
O больше числа знаков •, по крайней мере, на единицу. Первый знак • в польском выражении (при просмотре слева направо) может появиться только после двух знаков O. Пронумеруем позиции между знаками O:OO 1 O 2 O 3 O4 … nx – 2 O nx – 1.
Максимальное число знаков •, которое может появиться в позиции, равно номеру позиции. Если польское выражение соответствует перечисленным выше свойствам, то ему соответствует дерево разрезов.
Хромосома H имеет вид: H = {gi|i = 1, 2, ..., n·}. В результате декодирования хромосомы строится польское выражение. Число генов в хромосоме равно n•, то есть числу знаков •. Значение гена gi колеблется в пределах от i до n•, то есть . Значение гена указывает номер позиции в польском выражении, в которую необходимо поместить знак •.
. Значение гена указывает номер позиции в польском выражении, в которую необходимо поместить знак •.
Например, пусть для n· = 4 имеется хромосома H = <4, 2, 2, 4>, nx = n· + 1 = 5. Польское выражение для этой хромосомы имеет вид: ООО•• О••.
Аффинное пространство поиска
Пусть имеется линейное векторное пространство (ЛВП), элементами которого являются n-мерные точки. Каждым любым двум точкам p и q этого пространства однозначным образом сопоставим единственную упорядоченную пару этих точек, которую в дальнейшем будем называть геометрическим вектором (вектором). p, q ∈ V (p, q) – геометрический вектор (упорядоченная пара).
Совокупность всех точек ЛВП, пополненную геометрическими векторами, называют точечно-векторным, или аффинным пространством. Аффинное пространство является n-мерным, если соответствующее ЛВП также является n-мерным.
Аффинно-релаксационная модель (АРМ) роя частиц – это граф, вершины которого соответствуют позициям роя частиц, а дуги аффинным связям между позициями (точками) в аффинном пространстве. Аффинность – мера близости двух агентов (частиц). На каждой итерации каждый агент pi переходит в аффинном пространстве в новое состояние (позицию), при котором вес аффинной связи между агентом pi и базовым (лучшим) агентом p* уменьшается. Переход агента pi в новую позицию xi(t + 1) из xi( t) осуществляется с помощью релаксационной процедуры.
Специальная релаксационная процедура перехода зависит от вида структуры данных (хромосомы): вектор, матрица, дерево и их совокупности, являющейся интерпретацией решений.
Лучшие частицы с точки зрения целевой функции объявляются центром притяжения. Векторы перемещения всех частиц в аффинном пространстве устремляются к этим центрам.
Переход возможен с учетом степени близости к одному базовому элементу либо к группе соседних элементов и с учетом вероятности перехода в новое состояние.
Во избежание при описании популяции (роя) путаницы будем в дальнейшем каждую хромосому, описывающую i-е решение популяции, обозначать как Hi(t) = {gil|l = 1, 2, …, n}. Причем каждая Hi( t) имеет описанную выше структуру. В рассматриваемом случае позиция xi(t) соответствует решению, задаваемому хромосомой Hi(t), то естьxi(t) = Hi(t) = { gil |l = 1, 2, …, n}. Аналогично x*i(t) = Нi*(t) = {g*il |l = = 1, 2, …, n}, x*(t) = Н*(t) = {g* l|l = 1, 2, …, n}. Число осей в пространстве решений равно числу n генов в хромосомах Нi(t), Нi*(t), Н i*(t). Точками отсчета на каждой оси l являются целочисленные значения генов.
Механизмы перемещения частиц в аффинном пространстве поиска
Каждая частица перемещается в новую позицию. Новая позиция в канонической парадигме роя частиц определяется как:
xi (t+1) = xi(t) + vi(t + 1), (1)
где vi(t + 1) – скорость перемещения частицы из позиции xi(t) в позицию xi(t + 1). Начальное состояние определяется как xi(0), vi(0) [1].
Приведенная формула представлена в векторной форме. Для отдельного измерения j пространства поиска формула примет вид:
xij (t + 1) = xij(t) + vij(t + 1), (2)
где xij(t) – позиция частицыpi в измерении j; vij(t + 1) – скорость частицы pi измерении j.
Введем обозначения:
– xi (t) – текущая позиция частицы, f i(t) – значение целевой функции частицы pi в позиции xi( t);
– x* i (t) – лучшая позиция частицы pi, которую она посещала с начала первой итерации, а f*i(t) – значение целевой функции частицы pi в этой позиции (лучшее значение с момента старта жизненного цикла частицы pi);
– x* (t) – позиция частицы роя с лучшим значением целевой функции f*(t) среди частиц роя в момент времени t.
Тогда скорость частицы pi на шаге (t + 1) в измерении j вычисляется как:
vij (t + 1) = w∙vij(t)+ k1∙rnd(0,1)∙(x*ij(t) – xij(t)) + k2∙rnd (0,1)∙(xj(t)-xij(t)), (3)
где rnd(0,1) – случайное число на интервале (0,1); (w, k 1, k2) – некоторые коэффициенты.
Скорость vi(t + 1) рассматривается как средство изменения решения.
В отличие от канонического метода роя частиц в рассматриваемом случае скорость vi(t + 1) не может представляться в виде аналитического выражения. В качестве аналога скорости vi(t + 1) выступает оператор направленной мутации (ОНМ), суть которого в изменении целочисленных значений генов в хромосоме Нi( t). Перемещение частицы pi в новую позицию означает переход от хромосомы Н i(t) к новой – Нi (t+1) c новыми целочисленными значениями генов gil, полученными после применения ОНМ.
По аналогии с каноническим методом роя частиц позицию x*i(t) будем называть когнитивным центром притяжения, а позицию x*(t ) – социальным центром притяжения. Когнитивный центр выступает в роли индивидуальной памяти о наиболее оптимальных позициях данной частицы. Благодаря социальному центру частица имеет возможность передвигаться в оптимальные позиции, найденные соседними частицами.
В качестве оценки степени близости между позициями xi(t) и xz( t) будем использовать величину Siz расстояния между хромосомами Нi(t) и Н z(t):
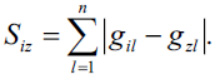 (4)
(4)
Целью перемещения хромосомы Нi(t) в направлении хромосомы Нz(t) является сокращение расстояния между ними.
Суть процедуры перемещения, реализуемой ОНМ, заключается в изменении разности между значениями каждой пары генов (gil, gzl) двух хромосом, l =1, 2, …, n.
Перемещение частицы из позиции Нi(t) в позицию Нi(t + 1) под воздействием притяжения к позиции Нz(t) осуществляется путем применения ОНМ к Нi( t) следующим образом. Последовательно просматриваются (начиная с первого) локусы хромосом Нi(t) и Нz(t), и сравниваются соответствующие им гены. Если в ходе последовательного просмотра локусов в текущем локусе l выпадает с вероятностью P событие «мутация», то ген gil(t) Î Н i(t) мутирует.
Пусть Riz(t) – число локусов в хромосомах Нi(t) и Нz(t), в которых значения генов 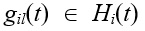 и
и 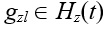 не совпадают.
не совпадают.
Вероятность мутации Р зависит от расстояния Siz(t) между позициями и определяется следующим образом:
Р = α × Riz (t) / n, (5)
где α – коэффициент; n – длина хромосомы.
Таким образом, чем больше число Riz(t ) несовпадений значений генов между позициями Нi(t) и Нz(t), тем больше вероятность, что значение gil(t) будет изменено.
Простой лотереей L (y1, р, y2) назовем вероятностное событие, имеющее два возможных исхода – y1 и y2, вероятности наступления которых обозначим, соответственно, через Р и (1 – Р) . Другими словами, с вероятностью Р лотерея L(y1,р, y2) = y 1, а с вероятностью (1 – Р) лотерея L(y1, р, y 2) = y1. Ожидаемая (или средняя) цена лотереи определяется по формуле рy1 + (1 – р)y2. Как уже указывалось выше, позиции задаются хромосомами. Позициям x(t),xi(t), x*i( t) xсi(t) соответствуют хромосомы Н*(t) = {g*l(t)||l = 1, 2, …, nl}, Нi(t) = {gil(t)|l = 1, 2, …, nl}, Н*i(t) = {g*il(t)|l = 1, 2, …, nl}, Нсi(t) = {gсil(t)|l = 1, 2, …, ni}.
Значения генов новой позиции частицы рi в результате мутации определяются как:
gil (t + 1) = gil(t), если (gil(t) = gzl(t));
gil (t + 1) = gil(t) +L(1, р, 0), если (gil(t) < gzl(t)); (6)
gil (t + 1) = gil(t) –L(1, р, 0), если (gil(t)) > gzl(t)).
Для учета одновременного тяготения частицы pi к лучшей к позиции x*(t) среди частиц роя в момент времени t и к лучшей позиции x*i(t) частицы pi, которую она посещала с начала первой итерации, формируется виртуальный центр (позиция) притяжения xc i(t) частицы pi. Формирование виртуальной позиции xc i(t) осуществляется путем применения процедуры виртуального перемещения из позицииx*i(t) в виртуальную позицию xci(t) по направлению к позиции x*(t). После определения центра притяжения xc i(t) частица pi перемещается в направлении виртуальной позиции xci(t) из позицииxi(t) в позицию x i(t + 1).
После перемещения частицы pi в новую позицию xi(t + 1) виртуальная позиция xci(t) исключается.
Локальная цель перемещения частицы pi – достижение ею позиции с наилучшим значением целевой функции. Глобальная цель роя частиц – формирование оптимального решения задачи.
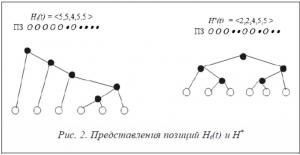
Пример. На рисунке 2 представлены две позиции – Hi(t) и H*(t) . Приведены представления каждой позиции в виде хромосомы, польской записи и дерева.
Частица pi перемещается из позиции Hi(t) в направлении позиции H*.
H* (t) – Hi(t) = <2, 2, 4, 5, 5> – <5, 5, 4, 5, 5> = <–3, –3, 0, 0, 0>. Si = 6.
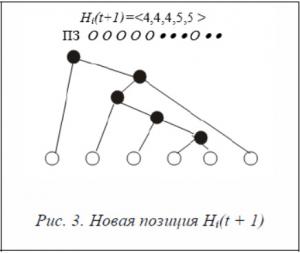
Δi(t + 1) = <–1, –1, 0, 0, 0>.
Hi (t + 1) = Hi(t) + Δ i(t + 1) = <5, 5, 4, 5, 5> + <–1, –1, 0, 0, 0> = <4, 4, 4, 5, 5>.
На рисунке 3 приведены новая позиция Hi(t + 1) и соответствующее дерево.
Заключение
Предложена композитная архитектура многоагентной системы бионического поиска на основе интеграции роевого интеллекта и генетической эволюции. Связующим звеном такого подхода является единая структура данных, описывающая решение задачи в виде хромосомы. Ключевая проблема, которая была решена в данной работе, связана с разработкой структуры аффинного пространства позиций, позволяющей отображать и осуществлять поиск интерпретаций решений с целочисленными значениями параметров. В отличие от канонического метода роя частиц для уменьшения веса аффинных связей путем перемещения частицы pi в новую позицию аффинного пространства решений разработан оператор направленной мутации, суть которого заключается в изменении целочисленных значений генов в хромосоме. Разработаны новые структуры хромосом для представления решений.
На основе рассмотренной парадигмы разработана программа разбиения ГАР. Для проведения экспериментов программы ГАР была использована процедура синтеза контрольных примеров с известным оптимумом Fопт по аналогии с известным методом BEKU (Partitioning Examples with Tight Upper Bound of Optimal Solution) [12]. Оценкой качества служит величина Fопт/ F – степень качества, где F – оценка полученного решения. Исследования показали, что число итераций, при которых алгоритм находил лучшее решение, лежит в пределах 120–135. Алгоритм сходится в среднем на 130-й итерации. В результате проведенных исследований установлено, что качество решений у гибридного алгоритма на 10–12 % лучше качества решений генетического и роевого алгоритмов по отдельности. Эксперименты показали, что увеличение популяции М больше 120 нецелесообразно, так как это не приводит к заметному изменению качества. Вероятность получения глобального оптимума составила 0,96. В среднем запуск программы обеспечивает нахождение решения, отличающегося от оптимального менее, чем на 2 %. Временная сложность алгоритма при фиксированных значениях M и T лежит в пределах О(n). Общая оценка временной сложности лежит в пределах О(n 2) – О(n3).
Работа выполнена при финансовой поддержке гранта РФФИ № 18-07-00737 А.
Литература
1. Clerc M. Particle swarm optimization. London, ISTE, 2006, 198 р.
2. Kennedy J., Eberhart R.C. Particle swarm optimization. Proc. IEEE Intern. Conf. Neural Networks, 1995, pp. 1942–1948.
3. Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой. М.: Изд-во МГТУ им. Н.Э. Баумана, 2014. 448 с.
4. Wang X. Hybrid nature-inspired computation method for optimization Thes. doctoral dissertation. Helsinki Univ. of Technology Publ., 2009, 161 p.
5. Raidl G.R. A unified view on hybrid metaheuristics. LNCS, 2006, Springer, Verlag, рр. 1–12.
6. Blum C., Roli A. Metaheuristics in combinatorial optimization: overview and conceptual comparison. ACM Comp. Surveys, 2003, no. 35, pp. 268–308.
7. Лебедев Б.К., Лебедев О.Б. Гибридный биоинспирированный алгоритм решения задачи символьной регрессии // Изв. ЮФУ. Технич. науки. 2015. № 6. С. 28–41.
8. Лебедев Б.К., Лебедев В.Б. Покрытие методом роя частиц // Интегрированные модели и мягкие вычисления в искусственном интеллекте: матер. VI Междунар. науч.-практич. конф. 2011. С. 611–619.
9. Sha D.Y., and Cheng-Yu. A hybrid particle swarm optimization for job shop scheduling problem. CAIE, 2006, vol. 51, is. 4, pp. 791–808. DOI: 10.1016/j.cie.2006.09.002.
10. Лебедев Б.К., Лебедев О.Б., Лебедева Е.М. Распределение ресурсов на основе гибридных моделей роевого интеллекта // Науч.-технич. вестн. ИТМО. 2017. Т. 17. № 6. С. 1063–1073.
11. Лебедев Б.К., Лебедев В.Б. Трассировка на основе метода роя частиц // XII национальн. конф.
по искусствен. интеллекту (КИИ-2010): тр. конф.: В 2 т. М.: Физматлит, 2010. Т. 2. С. 414–422.
12. Cong J., Romesis M., and Xie M. Optimality, scalability and stability study of partitioning and placement algorithms. Proc. Intern. Sympos. Physical Design, 2003, pp. 88–94. URL: http://www.cecs.uci.edu/~papers/compendium94-03/papers/2003/ispd03/htmfiles/sun_sgi/ispdabs.htm (дата обращения: 20.02.2019).
Comments