При управлении технологическими процессами конечные автоматы использовались в основном для описания дискретных процессов. Для непрерывных химико-технологических процессов (ХТП) рассматривались режимы пуска и останова оборудования, различные переключения аппаратов при переходе с выпуска одного продукта на другой, вывода на рабочий режим при возникновении нештатной ситуации и т.д.

В данной работе рассматривается подход, который позволяет на основе метода разделения состояний построить дискретную модель для непрерывных химико-технологических систем (ХТС), а затем осуществить разработку системы управления на основе применения теории конечных автоматов.

Современные системы безопасности химических производств являются сложными человеко-машинными системами, которые можно подразделить на взаимосвязанные подсистемы. Соподчинение между ними увязывается иерархической структурой, состоящей из нескольких уровней иерархии [1, 2].

К системам управления технологической безопасностью химических производств предъявляют широкий спектр требований в соответствии с их целевым назначением по выполнению технико-экономических, социальных и экологических критериев в условиях существующих в настоящее время жестких ограничений на материально-энергетические, трудовые, информационные и временные ресурсы.

Современная технология создания систем управления обеспечением безопасности химических производств предполагает построение систем, имеющих повышенную живучесть (гибкость, маневренность, адаптивность, самоорганизуемость, оперативность, конкурентоспособность и т.д.) на основе ее рациональной организации в органической связи с системой принятия решений (СПР) в условиях изменяющейся окружающей среды.

Как уже указывалось, при создании систем обеспечения безопасности химических производств на основе дискретных моделей необходимо руководствоваться принципами классификации состояний элементов; декомпозиции; иерархичности распознавания неисправностей и аварийных состояний; прогнозирования изменения состояний химического производства; принципом управления критическими режимами.

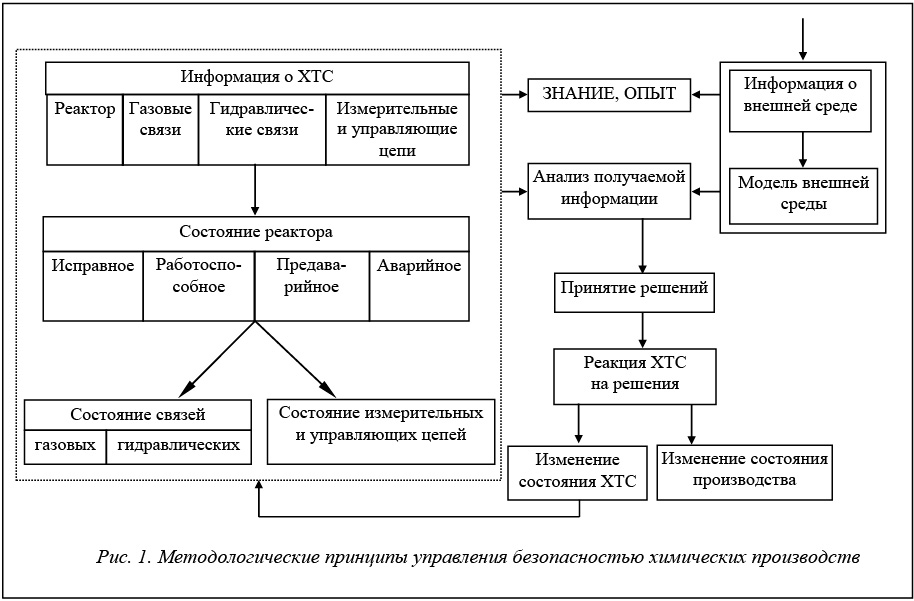
В соответствии с принципом декомпозиции в химических процессах выделяются четыре подсистемы: реактор процесса; гидравлические связи, по которым перемещаются жидкие среды; газовые связи, по которым перемещаются газовые среды; измерительные и управляющие цепи АСУ технологическими процессами.

Распознавание неисправностей и аварийных состояний в соответствии с принципом иерархичности начинается с изучения режима протекания процесса в аппарате и определения его состояния. По состоянию технологического процесса выявляются неисправные технологические структуры (гидравлические, газовые связи и цепи АСУ технологическими процессами).

Принципы иерархичности и декомпозиции играют существенную роль в системе управления диагностикой с точки зрения последовательного раскрытия неопределенности, присутствующей при поиске первопричин возникновения неисправностей. На основе их применения порождается удобная структура процедуры принятия решений и оценки последствий тех или иных управляющих воздействий.

На рисунке 1 показана реализация применения данных принципов для ХТП.

Основная особенность управления процессом диагностики состояний непрерывных ХТП заключается в том, что управление основано на анализе событийных процессов, происходящих в технологической системе, и на каждом уровне иерархии принятия решений необходимо оценивать риск принимаемых решений. При этом часто необходимо использовать дополнительную информацию для каждого объекта ХТС, подвергаемого диагнозу. Это относится и к диагностике связей реактора, и к поиску неисправностей в конкретных аппаратах, элементах их конструкций, и к системам управления. В случае значительного влияния случайных возмущений возникает необходимость определять риск и в оценке состояний основных аппаратов ХТП.

Автоматный подход, развиваемый в данной работе, позволяет отслеживать событийные процессы, происходящие в ХТС, для нормального хода технологического процесса, прогнозировать раннее зарождение нарушений в системе и гибко реализовывать выполнение принципа прогнозирования состояний химического производства.

Принцип управления критическими режимами реализуется за счет поддержания рабочей точки процесса в области работоспособного состояния с заданным запасом работоспособности на основе выбора соответствующих управляющих воздействий.

В соответствии с этими принципами осуществляется структурная декомпозиция технологической схемы, в результате которой выделяются один или несколько ключевых аппаратов, определяются состояния данных структурных элементов. На первом уровне решения задачи управления диагностикой по этим состояниям принимают решение о наличии дефектов в соответствующих аппаратах, а также делают предположение о возможных неисправностях в газовых или гидравлических связях.

На следующем уровне иерархии управляют определением наличия неисправностей в газовых или в гидравлических связях либо в системах контроля и регулирования.

Далее осуществляется локализация дефекта в конкретном техническом устройстве (управление поиском первичной неисправности).

Решения по управлению технологической безопасностью на основе диагностического многоуровневого анализа принимаются с учетом возможных прогнозируемых состояний технологического процесса и информации о состоянии внешнего окружения.

Структура раскрытия неопределенности

Процесс управления технической диагностикой можно определить как решение задачи определения пути прохождения от зарегистрированных возмущений к их источникам. Таким образом, задача управления диагностикой является поисковой задачей большой размерности.

Доказано [3], что любой интеллектуальный поиск связан со структурированием поискового пространства с целью ограничения множества возможных направлений движения. В связи с этим для целей структуризации применяются принципы декомпозиции, и далее решение задачи поиска представляется как многоуровневая иерархическая задача.

В общем случае работоспособность технологического агрегата описывается множеством состояний A, которые определяются количеством диапазонов технологических режимов работы измеряемых Zn и неизмеряемых Xm переменных состояния Y={Zn}{Xm} (Yi – диагностические переменные). В общем случае диагностические переменные в данной работе представляются подмножеством множества переменных состояния. Они выделяются из множества переменных состояния, так как несут наибольшую информационную нагрузку. Исправному состоянию агрегата соответствует удовлетворение значений всех диагностических переменных диапазонам желаемых значений: " Y: Yi=y½yÎ[d; d], где y – текущее значение диагностической переменной Yi, Î[d; d] – интервал допустимых значений.

 На первом уровне диагноз состояния ХТП делается на основе либо дискретных моделей реакторных узлов, которые были получены на основе линеаризации основных уравнений материальных и тепловых балансов для нормального режима работы, либо построения нечетко определенных дискретных моделей. Нарушение этих ограничений в дискретных моделях реакторных узлов или индекс состояний (нечетко определенные модели) говорит о появлении неисправности в технологии. Причем каждое конкретное ограничение показывает, какая диагностическая переменная состояния вышла за диапазон нормальной работы, что соответствует появлению нарушения по диагностической переменной (НДП).

На втором уровне иерархии делается диагноз состояния связей реактора. Если появлению неисправного состояния по i-й переменной состояния поставить в соответствие значение логической переменной P(Yi), равное 1, а отсутствию НДП – равное 0, то анализ состояния агрегата по вектору переменных Y можно заменить анализом по вектору признаков P:

Y®P=[P(Y1), P(Y2), ... , P(Yi), ...½P(Yi)=p],

где p {0;1}, i=1, card Y.

Обозначим множество технологических связей, действительно содержащих неисправные элементы, Ct. Тогда процедура диагноза сводится к решению логического уравнения

F:Pt®Ct,                                                            (1)

pk=1,     ciÎCk

где F – предикатная функция вида F= Ù (Ú ci), ci – событие, заключающееся в неисправности отдельной технологической связи или узла; Ck – множество технологических подсистем, неисправность которых может вызвать нарушение нормального режима работы по k-й переменной. Решение уравнения (1) может быть найдено с помощью булевского подхода в виде

C* = Ù {ci½ciÎCk},                                           (2)

PkÎP*,

если возникновение любой неисправности s в связи ci является необходимым и достаточным условием появления всех НДП Pk, таких, что ciÎCk, то есть если

VsÎS : (pk=0) « (Ck Ù C* = Æ);                   (3)

VsÎS : (pk=1) « (Ck Ù C* = C*),                   (4)

где S – множество диагностируемых неполадок; Æ – пустое множество.

На практике это означает требование взаимонезависимости и однозначности связей между проявлениями и источниками неполадок, что в большинстве случаев неприемлемо для реального применения к процессам химической технологии.

Учет неопределенности в диагностических процедурах позволяет смягчить требования к взаимонезависимости и однозначности связей. Тогда задачей второго уровня управления диагностическим процессом становится оценка вероятности диагнозов из множества C, полученного в результате решения задачи декомпозиции химического производства, в случае байесовского подхода

"j = 1, card C: Qj = Q(cj|P), Qj Î [0; 1]          (5)

или подхода на основе нечетких множеств [4, 5].

В различных работах чаще всего предлагается следующий способ представления знаний для решения этой задачи:

"i=1, card P, "j=1, card C: P(Yi)=pi®Q(cj|P(Yi))=Q(cj|pi).                          (6)

Выражение (6) представляет собой записанную в общем виде интеллектуальную диагностическую модель технологического процесса. Использование этой модели обычно ограничивается требованиями взаимозаменяемости и однозначности диагностических признаков, что в большинстве случаев неприемлемо для реального применения к процессам химической технологии.

Использование методов теории свидетельств [6, 7] вместо традиционных методов нечетких множеств или теоремы Байеса позволяет снять требование независимости диагностических признаков при обработке модели вида (6). В работах данного направления сделана попытка подойти к понятию неопределенности в задачах управления технической диагностикой с наиболее общей точки зрения, обеспечивающейся использованием теории свидетельств.

Основа метода заключается в том, что некоторая мера вероятности может быть отнесена не только к отдельным элементам множества событий в предметной области, но и в целом к некоторому подмножеству этого множества. В соответствии с распределением вероятностей для решаемой задачи будет называться весовая функция m(Ai) [0,1], такая что

m(Æ)=0 и S m(Ai)=1,

             AiÎC

где Ai – событие, состоящее в неисправности одной или нескольких связей; C – полная группа событий, являющихся результатом диагноза. Исходя из распределения вероятностей, можно рассчитать ряд дополнительных характеристик для оценки результатов диагностических процедур.

Степень уверенности в наличии неисправного элемента в составе связей, принадлежащих подмножеству АiÎC:

Bel(Ai) = S m(Aj).                                                   (7)

               AjÎAi

Такая функция обладает следующими свойствами: Bel(Æ)=0; Bel(Ai)Î[0;1]; Bel(C)=1.

Степень сомнения в наличии неисправного элемента в составе связей, принадлежащих подмножеству АiÎC:

Dou(Ai)=Bel(ùAi)

(ù – символ отрицания).

Степень правдоподобия наличия неисправного элемента в составе связей, принадлежащих подмножеству Аi Î C:

Pl(Ai)=1-Dou(Ai)=1-Bel(ùAi)=1- S m(ùAj).          (8)

                                                       AjÎ Ai

По аналогии с теорией вероятности величины Bel(Ai) и Pl(Ai) можно рассматривать как нижнюю ~p(Аi), так и верхнюю ~p(Аi) границы вероятности наличия неисправного элемента в составе связей, принадлежащих подмножеству АiÎC, предполагая существование некоторой истинной вероятности p(Аi) Bel(Ai)=~p(Ai)<p(Ai)<~p(Ai)=Pl(Ai). Такие интервальные характеристики называют очевидностными интервалами.

Для нахождения решения уравнения (1) с помощью теории свидетельств будем рассматривать результаты решения задачи экспертной классификации как распределение мер вероятности по множеству событий Ci, активизированному НДП P(Yi)=1. Для этого нормализуют результаты экспертной оценки, предварительно преобразовав множество Ci таким образом, чтобы

Vcj,ck Ci:{(cj;mi(cj),(ck;mi(ck))}®{(cjvck;mi(cj))},              (9)

                    j¹k,

            mi(cj)=mi(ck),

в результате чего два равновероятных события сводятся к одному и множество Ci преобразуется в множество C·i.

После выполнения процедуры (9) нормализованная мера вероятности для событий из преобразованного множества C·i определяется как

mi(Aj)=mi(Aj) / S mi(Ak).                                                      (10)

    AkÎC·i

При использовании подхода для объединения различных свидетельств с распределениями вероятностей m1 и m2 в пользу одной гипотезы используется правило Демпстера [7]:

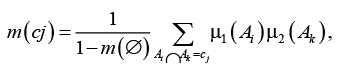                                                                                                                                                                                 (11)

где мера вероятности, приходящаяся на пустое множество

m(Æ)=S m1(Ai) m2(Ak).

    AiÇAk=Æ

Вопрос о том, каким образом происходит принятие решения о наличии НДП, является существенным для конечной цели диагностики. Пусть в течение интервала времени Т=[t-;t+] на основе дискретной модели было определено нарушение ограничений по некоторым диагностическим переменным состояния Yi=[y-;y+]. Кроме того, для каждой диагностической переменной состояния задан диапазон нормальной работоспособности в виде интервала Di=[d-;d+]. Для определения НДП по i-й переменной рассчитывается индикаторная функция P(Yi), характеризующая вероятность НДП:

Si"+"=:         y+ £ d+ ® Pi = 0;                                         (12)

                   y_ ³ d+ ® Pi = 1;       

                   y_. < d+ < y+ ® Pi = (y+- d+)/( y+- y_).

                                      

Si"-"=:         y_ ³ d_® Pi = 0;                                             (13)

                   y+ £ d_® Pi = 1;        

                   y_. < d_ < y+ ® Pi = (d_- y_.)/(y+- y_).

                                      

Si"+  -"=:      (d_£ y_) Ù (y+ £ d+ ) ® Pi = 0;                (14)

                   (y_ ³ d+) Ú (y+ £ d_ ) ® Pi = 1;              

                   y_ < d+ < y+ ® Pi = (y+- d+)/(y+- y_);      

                   y_ < d_ < y+ ® Pi = (d_- y_.)/(y+- y_),      

где Si – направление развития отказа, характерное для i-й переменной. Функция P(Yi) из булевской функции превращается в непрерывную функцию, определенную на интервале [0;1]. Если значение индикаторной функции P(Yi) отлично от 0, то активизируется нечеткое множество возможно неисправных связей Ci={(Aj;mi(Aj))}.

Обозначим как C полное множество возможных исходов диагноза, включая состояние нормальной работоспособности агрегата, а ui – степень сомнения в НДП по i-й переменной: ui=1-P(Yi). Тогда мера уверенности, приходящаяся на ui, относится ко всему множеству C в целом и меры вероятности, относящиеся к элементам множества Ci, перераспределяются следующим образом:

m·i(Aj)=mi(Aj) P(Yi), m·(C)=ui.                                         (15)

Такой подход увеличивает уровень неопределенности в СПР, но существенно повышает чувствительность диагностической системы и в то же время позволяет достаточно эффективно отсекать ложные гипотезы при использовании оценок в виде очевидностных интервалов.

В диагностике существуют два типа ошибок, возникающих при проверке диагностических гипотез: ошибки 1-го рода – это ошибки типа «ложная тревога»; ошибки 2-го рода – «отсутствие тревоги при наличии неполадки». При использовании традиционных методов решения уравнения (2) невыполнение условия необходимости (4) приводит к ошибкам 2-го рода, а невыполнение условия достаточности
(5) – к ошибкам 1-го рода.

Для того чтобы избежать ошибок 1-го рода, в СПР используется пороговый уровень доверия для отсекания маловероятных гипотез. Из опыта применения видно, что хорошие показатели диагностических процедур достигаются при уровне доверия от 10 до 20 % уверенности.

В предложенной постановке задача распознавания неисправных технологических связей химического производства может решаться в условиях существенной неопределенности, что соответствует наиболее часто встречающимся реальным диагностическим задачам.

На третьем уровне принятия решений осуществляется поиск первичной неисправности. Основой решения задачи нахождения первичной неисправности является анализ неисправной технологической подсистемы, основанный на знаниях, – так называемый качественный анализ, который базируется на использовании эвристических правил и нечеткого дерева отказов.

Качественный анализ технологических связей осуществляется на основе причинно-следственного графа, после того как была определена вероятность наличия источника неполадок в каждой технологической связи. Для этого задача диагностики дефектов химического производства рассматривается как задача обратного моделирования. В такой постановке общая модель диагностического процесса W может быть представлена как структура вида

W=<F, S, M>,                                                            (16)

где F={Fi}, i=1, I – множество наблюдаемых признаков неисправностей; S ={Sj}, j=1, J – множество состояний технологического оборудования; M={Mk}, k=1, K – множество путей развития диагностической процедуры. И тогда задача диагностики представляет собой поисковую задачу размерностью I´J´K. Структуризация диагностического поиска позволяет преобразовать (14) в граф, узлами которого являются элементы SjÎS, а дуги определяются множеством M.

Определенный таким образом граф строится для каждой технологической связи и называется диагностическим причинно-следственным графом (ДПСГ). Множество терминальных (то есть не связанных с последующими) узлов StÎS в ДПСГ представляет собой множество диагностируемых неполадок в данной технологической связи.

Задача диагностирования сводится к выделению в ДПСГ дерева, содержащего проходимые дуги, корнем которого является терминальный узел (или узлы) – множество возможных неисправностей, а листьями – множество начальных фактов (признаков). Начальное множество фактов соответствует текущему состоянию диагностируемой связи и определяется в начале процедуры диагностирования. В зависимости от результатов диагностирования на верхних уровнях гибридной автоматизированной системы технической диагностики и квалификации пользователя возможна различная степень локализации неисправности на начальном этапе диагностирования.

Оценка риска возникновения аварийных состояний на основе вероятностного подхода

Если на основе оценивания неисправностей и состояний ХТП и ХТС будет выявлено, что объект находится в аварийном состоянии, то необходимо выявить все возможные аварийные ситуации и факторы риска, рассмотреть возможные сценарии развития аварийных ситуаций, затем дать количественную оценку риска и оценить все виды ущербов от реализации каждого из сценариев развития аварийных ситуаций. Данный подход рассматривается, например, в [8].

Под аварийной ситуацией (Sj) понимается сочетание условий или обстоятельств, появление которых может привести к возникновению фактора (факторов) риска (Fi) – причины, движущей силы, способной привести к негативному воздействию на различных реципиентов. Каждая ситуация может привести как к одному фактору риска, так и к нескольким сразу, которые, в свою очередь, могут привести к возникновению одного или нескольких видов риска (Rk), в зависимости от характера наносимого ущерба. Типовые аварийные ситуации, приводящие к одинаковым факторам риска, можно объединить в аварии.

Для количественной оценки риска разработана модель, позволяющая определить две составляющие риска: вероятностную и стоимостную.

Пусть Pj – вероятность возникновения j-й ситуации; Fij – вероятность возникновения i-го фактора риска в j-й ситуации; Ekij – вероятность k-го вида риска от i-го фактора риска в j-й ситуации, тогда вероятность того, что возникновение i-го фактора риска в j-й ситуации приведет к k-му виду риска, определяется по соотношению

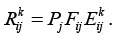                                                       (17)

Вероятность возникновения k-го вида риска в j-й ситуации от всех факторов риска определяется по соотношению

                             (18)

где М – количество факторов риска; К – количество видов риска, К = 3 – риск экологический, социальный и экономический.

Вероятность того, что риск k-го вида обязательно возникнет при реализации хотя бы одной ситуации, определяется по соотношению

       (19)

Соотношение (19) характеризует вероятностную составляющую риска.

Для экологического и экономического риска можно рассчитать и стоимостную составляющую риска – ущерб от j-й ситуации, выраженный в денежном эквиваленте, объединенный с вероятностью возникновения этой ситуации.

Пусть Ckj – величина ущерба k-го вида при возникновении j-й ситуации, тогда выражение для риска
k-го вида в стоимостном выражении для данной ситуации запишется в виде

                 (20)

Тогда интегральный показатель риска (суммарный риск k-го вида) будет равен:

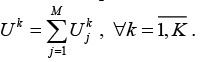                                                (21)

Соотношение (21) позволяет оценить риск в стоимостном выражении.

Общий риск всех видов в стоимостном выражении составит:

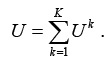                                                                     (22)

Для определения вероятностей возникновения аварийных ситуаций используются прежде всего соответствующие отраслевые банки статистических данных по характерным отказам и авариям. При отсутствии статистически значимой информации определение вероятности проводят с использованием причинно-следственных закономерностей (логик) возникновения аварийных ситуаций и развития аварий
из совокупности промежуточных событий, то есть на базе разработки соответствующих сценариев.
Поскольку число таких сценариев может быть весьма значительным, а их реализация взаимозависимой, для интегрального определения вероятности аварии на сложных объектах необходимо использовать специальные методики построения деревьев событий или деревьев отказов. Эти методики широко освещены в специальной литературе [9, 10].

Эффективность этих действий в значительной мере зависит от правильного понимания возможностей достоверного прогноза физических эффектов, связанных с авариями, сценариев их развития и масштабов воздействия на окружающую среду. Уровень материальных затрат на снижение масштабов распространения полей физического воздействия на окружающую среду должен увязываться по мере своей значимости с общей стратегией уменьшения риска для рассматриваемой группы воздействия.

Пример расчета риска. С использованием вышеизложенного подхода к оценке риска был рассчитан показатель риска для одного из производств нефтеперерабатывающего завода – производства полипропилена [11]. При анализе этого производства как объекта риска выявлено, что для производства полипропилена можно выделить 4 основных типа аварий, к которым могут привести те или иные аварийные ситуации: аварии, связанные: 1) с пожаром, взрывом в узле хранения и дозировки; 2) с загазованностью (с выделением вредных газов, в основном пропилена) на территории установки, что, в свою очередь, может привести к загоранию и пожару; 3) с появлением пыли полипропилена на установке; 4) с загазованностью в помещении хранения баллонов с гасителем реакции (CO+N2). Наибольшую опасность для окружающей среды и обслуживающего персонала представляет авария, связанная с пропиленом, который может выделяться в большом количестве и образовывать взрывоопасные смеси с воздухом. В качестве опасных ситуаций, связанных с появлением пропилена на территории установки, были выделены 14 основных (типовых) аварийных ситуаций. Последние связаны с разгерметизацией различного типа оборудования и трубопроводов. Например, ситуация S1 – с разгерметизацией холодильника, в котором охлаждается подаваемый на установку пропилен; S2 – с разгерметизацией реактора предполимеризации; S3 – с разгерметизацией основного реактора и т.д. Каждая из выделенных ситуаций приводит к появлению на установке большого количества газа пропилена, который образует с воздухом взрывоопасную смесь и следовательно, является причиной трех основных факторов риска: F1 – многократное превышение предельно допустимых концентраций вредных веществ (пропилена) в воздухе; F2 – барический взрыв, связанный с тем, что полимеризация происходит в аппаратах под давлением; F3 – образование взрывоопасной смеси, взрыв, пожар. Каждый из перечисленных факторов, в свою очередь, обусловливает наличие тех или иных рисков. Более подробно были исследованы два вида риска: риск токсикологического воздействия на обслуживающий персонал, находящийся в момент аварии на территории установки, и риск воздействия на окружающую среду, который рассчитывался как плата за возможный нанесенный ущерб. Диаграмма этих ситуаций и связанных с ними факторов риска представлена на рисунке 2 (в данном случае рассматривался только экологический риск).

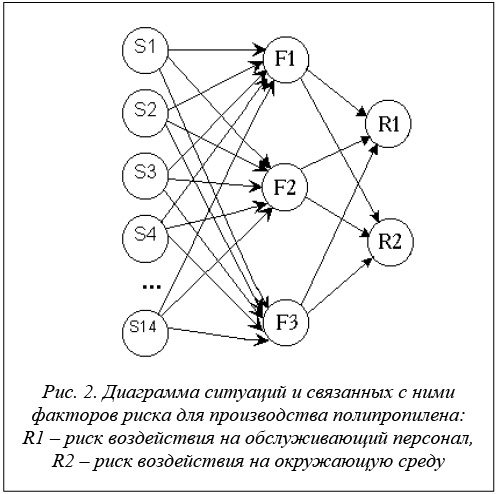
Для того чтобы определить количество вышедшего газа и скорость, с которой происходит его выброс в той или иной аварийной ситуации (эти данные необходимы для нахождения максимально возможной концентрации вредного вещества, а также для определения платы за возможный ущерб, нанесенный окружающей среде), использовались приведенные далее соотношения.

Для инженерной оценки массового расхода газа при разрыве трубопровода может быть использовано уравнение Белла [12, 13]:

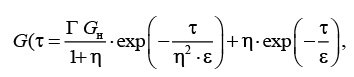                                      (23)

где G, Gн – соответственно текущий и начальный массовый расход (в момент разрыва), кг/с ; t – время, прошедшее с момента разрыва, с; Г – фактор инерционной задержки (@0,5); h – коэффициент сохранения массы; e – постоянная времени, с.

Начальный массовый расход рассчитывается в предположении о том, что в месте разрыва характер процесса истечения адиабатический:

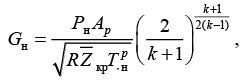                                           (24)

где Рн – давление газа в трубопроводе до разрыва, Па; Ар – площадь поперечного сечения разрыва, м2;
R – газовая постоянная (Дж/кг К); Тнр – температура газа в трубопроводе до разрыва, К; кр – коэффициент сжимаемости по условиям газа на срезе (выходе) при Ркр; Ткр.

Коэффициент сохранения массы рассчитывается по соотношению:

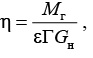                                                                                     (25)

где Мг – общая масса газа, способная вытечь из изолированной секции трубопровода (кг).

Выражение для постоянной времени (e) базируется на допущении об изотермическом характере процесса движения газа, имеющем место на большей части длины отсеченной секции трубопровода:

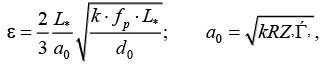                                (26)

где L* – длина отсеченного участка трубопровода, м; а0 – скорость звука в газе до разрыва, м/сек; fтр – коэффициент трения газа о стенки трубы.

Общая масса газа, которая может быть выброшена при разрыве, определяется из выражения:

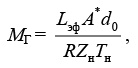                                                                       (27)

где Zн – коэффициент сжимаемости газа до разрыва при параметрах Рн, Тн; Lэф@1,3L* – эффективная длина участка трубопровода, учитывающая дополнительную массу газа, выбрасываемую за время, требующееся для полного закрытия запорной арматуры, м; А* – площадь поперечного сечения трубопровода.

Для оценки массового расхода газа при истечении «отверстие» из сосуда высокого давления используются формулы:

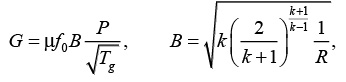                              (28)

где Р – давление; G – массовый расход: m – коэффициент расхода; f0 – площадь сечения отверстия; k=Cp/Cv – показатель адиабаты; V – объем сосуда.

Скорость истечения потока равна местной (для «сжатого» сечения при f=fmin=f0) скорости звука:

                                                            (29)

Максимальное значение приземной концентрации Сmах (мг/м3) при выбросе газовоздушной смеси из одиночного точечного источника при неблагоприятных метеорологических условиях на расстоянии Хмах от источника рассчитывается по уравнению

                                                             (30)

где А – коэффициент, зависящий от температурной стратификации атмосферы; М – масса вредного вещества, выбрасываемого в атмосферу в единицу времени, г/с. F – безразмерный коэффициент, учитывающий скорость оседания вредных веществ в атмосферном воздухе; m и n – коэффициенты, учитывающие условия выхода газовоздушной смеси из устья источника выброса; Н – высота источника выброса над уровнем земли, м (для наземных источников принимается равным 2 м); h – безразмерный коэффициент, учитывающий влияние рельефа местности; Т – разность между температурами выбрасываемой газовоздушной смеси и атмосферного воздуха, оС; V1 – расход газовоздушной смеси, м3/с.

Состояние загрязнения атмосферного воздуха [14] оценивается с помощью индекса загрязнения атмосферы Y, который рассчитывается по соотношению

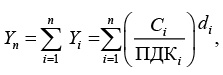                                             (31)

где Yi – единичный индекс загрязнения; Сi – концентрация вещества i; ПДКi – предельно допустимая концентрация вещества i; di – безразмерная константа приведения степени вредности вещества к вредности диоксида серы. В зависимости от класса опасности 1, 2, 3 или 4 значения di принимаются соответственно равными 1,7; 1,3; 1,0; 0,9; n – число вредных веществ, учитываемых в комплексном индексе загрязнения. Для расчета загрязнения на одно вещество (пропилен) соотношение соответственно упрощается.

Предложенная методика расчета была применена для определения вероятности появления той или иной концентрации опасного газа (пропилена) на установке производства полипропилена. В качестве исходных данных для 14 типовых аварийных ситуаций, представленных на рисунке 2, приводящих к аварии типа загазованности на территории установки, задавались частота возникновения нежелательного события (выброс в окружающую среду), количество выбросов опасных веществ в окружающую среду, технологические характеристики оборудования.

Для расчета токсического воздействия на обслуживающий персонал была определена вероятностная составляющая оценки риска по соотношениям (17–19). Для оценки массовых расходов и скоростей
выбросов использовались соотношения (23–29), а по методике [15] были рассчитаны максимальные разовые концентрации для аварийных ситуаций S1–S14 и определены уровни превышения ПДК. По соотношению (31) были определены индексы загрязнения атмосферы, а по соотношению (19) оценены вероятности их появления для рассматриваемой аварии на установке производства полипропилена при условии, что , которое соответствует превышению ПДК, то есть факту, что поражение точно произошло.

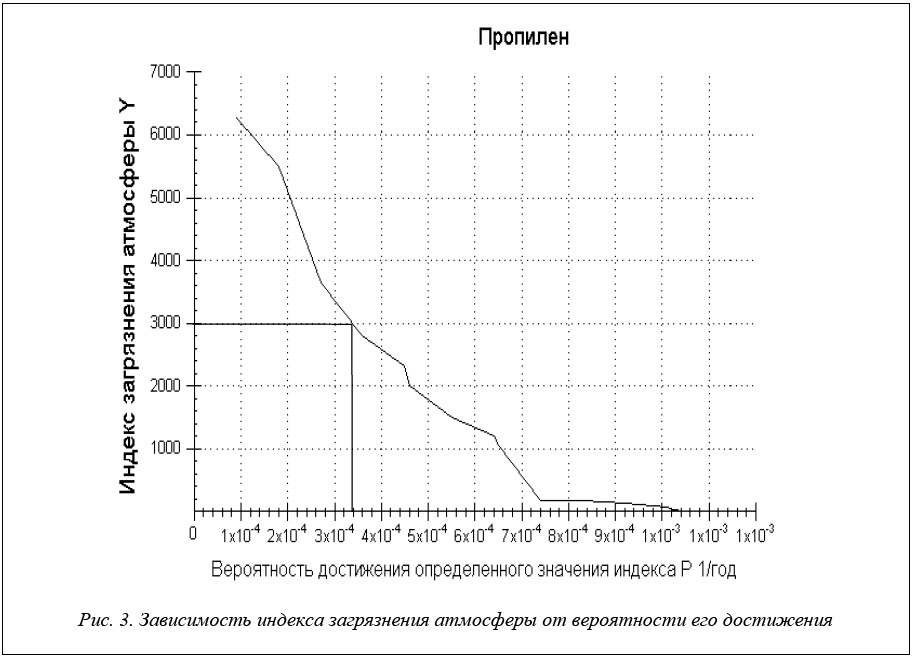
Результаты представлены на рисунке 3 в виде графика зависимости индекса загрязнения атмосферы Y от вероятности достижения определенного значения этого индекса P (1/год). Из графика видно, что более 90 % аварийных ситуаций приводят к значительному превышению ПДК (более чем в 103). А для значений вероятности более 3,5 10-4 индекс загрязнения атмосферы превышает 3000, что соответствует ЛК50.

Расчет риска нанесения ущерба окружающей среде проводился по методике [16]. В качестве исходных данных задавались: вероятности возникновения k-го вида риска в j-й ситуации (Rkj), количество выброшенных в атмосферу веществ (т). Рассчитывались ущербы Сkj, по соотношению (20) определялись стоимостные составляющие риска Ukj.

Суммарный годовой ущерб, который может быть нанесен окружающей среде в результате аварий, связанных с попаданием в атмосферу пропилена, составил 2558,87 руб./год.

Литература

1. Палюх Б.В., Богатиков В.Н., Пророков А.Е., Алексеев В.В. Приложения метода разделения состояний к управлению технологической безопасностью на основе индекса безопасности. Тверь: Изд-во ТГТУ, 2009. 368 с.
2. Палюх Б.В., Богатиков В.Н., Олейник А.Г., Алексеев В.В., Пророков А.Е. Новые технологии диагностики состояний и управления безопасностью промышленных процессов. Тверь: Изд-во ТвГТУ, 2012. 64 с.
3. Искусственный интеллект: В 3 кн. Кн. 2. Модели и методы: справочник; [под ред. Д.А. Поспелова]. М.: Радио и связь, 1990. 356 с.
4. Богатиков В.Н., Палюх Б.В., Пророков А.Е., Мартыненко И.Б. Методология управления технологической безопасностью непрерывных химико-технологических процессов: монография. РХТУ им. Д.И. Менделеева. Новомосковский институт, Новомосковск, 2005. 188 с.
5. Куперман В.Г. Разработка гибридных автоматизированных систем технической диагностики непрерывных химических производств (на примере производства азотной кислоты): автореф. дис. на соискание ученой ст. канд. техн. наук. М.: МХТИ им. Д.И. Менделеева, 1991. 16 с.
6. Shafer G. A Mathematical Theory of Evidence. Princeton: Princeton Univ. Press, 1976, 297 p.
7. Dempster A.E. A Generalization of Bayesian Inference. J. Roy. Statist. Soc. B., 1968, vol. 30, pp. 205–247.
8. Егоров А.Ф., Савицкая Т.В. Управление безопасностью химических производств на основе новых информационных технологий. М.: Химия. КолосС, 2004. 416 с.
9. Палюх Б.В. Основы построения и разработки автоматизированной системы управления эксплуатационной надежностью химических производств: дис. … докт. техн. наук (05.13.06). М., 1991. 360 с.
10. Хенли Э. Дж., Кумамото Х. Надежность технических систем и оценка риска. М.: Машиностроение, 1984. 528 с.
11. Егоров А.Ф., Савицкая Т.В., Макарова А.С., Сафонова Т.А., Богатиков В.Н. Методика оценки риска для предприятий химической и смежных отраслей промышленности // Управление безопасностью природно-промышленных систем. Вып. I. Апатиты: Изд-во КНЦ, 1998. С. 13–20.
12. Сафонов В.С., Одишария Г.Э., Швыряев А.А. Теория и практика анализа риска в газовой промышленности. М.: НУМЦ Минприроды России, 1996. 208 с.
13. R.P.Bell.Isopleth calculations for ruptures in sour gas piperline// Energy Processing Canada, 1978, July–August, p. 36–39.
14. Оценка и регулирование качества окружающей природной среды: учеб. пособие для инженера-эколога; [под ред. А.Ф. Порядина, А.Д. Хованского]. М.: НУМЦ Минприроды России, 1996. С. 93–96.
15. Ammar H., Huang Y.F., Liu R.W. Proc. Int. Symp. Circuit a. Syst. Kyoto. 1985, no. 2, pp. 743–746.
16. Методика расчета концентраций в атмосферном воздухе вредных веществ, содержащихся в выбросах предприятий. ОНД-86, Госкомгидромет. Л.: Гидрометиоиздат, 1987. 608 с.

MANAGEMENT OF TECHNOLOGICAL SAFETY OF CONTINUOUS
CHEMICAL-TECHNOLOGICAL PROCESSES ON THE BASIS OF DISCRETE MODEL

Palyukh B.V., Dr.Sc. (Engineering), Professor; Bogatikov V.N., Dr.Sc. (Engineering), Professor;
Alekseev V.V., Ph.D.  (Engineering), Associate Professor

(Tver State Technical University, Nikitin Quay 22, Tver, 170026, Russian Federation, is@tstu.tver.ru)

Vent D.P., Dr. Sc. (Engineering), Professor; Prorokov A.E., Ph.D. (Engineering), Associate Professor;
Sanaeva G.N., Senior Lecturer

(Novomoskovsk Institute of MUCTR. D.I. Mendeleev, Druzhby st. 8, Tula Reg., Novomoskovsk, 301665,
Russian Federation, k_vtit@dialog.nirhtu.ru);

Toichkin N.A., Ph.D. (Engineering), Associate Professor, toichkin@list.ru

(Kola branch of Petrozavodsk state University, Lesnaya st. 29, Murmansk Reg., Apatity,
184209, Russian Federation)

The paper focuses on the principles of technological safety. The characteristic features of the implementation of these principles to continuous processes of chemical technology. Given the definition of the diagnostic task as a multi-level, hierarchical task, shown decomposition of a chemical-technological systems, presents the technique of diagnostics of the state chemical-technological systems based on the discrete models that allow to predict the occurrence of gradual failures resulting from deterioration of the properties of substances involved in chemical-technological processes (for example, deterioration of the catalyst in the reactor), properties of devices (scale formation on heat exchanger surfaces), etc. The method of solution is obtained for the primary fault, which is based on a faulty analysis of the technological subsystem, knowledge-based, so – called qualitative analysis, which is based on the use of a fuzzy graph development hazards and is based on its hierarchical diagnosis chart. As a result, we have diagnostic causal graph.

Assesses the risk of failure States based on probabilistic approach.

Keywords: mathematical model, technological safety, process control, chemical-technological process, environment.