Использование кэш-систем является одним из приемов, направленных на согласование работы
разных по скорости устройств и повышение производительности вычислительных комплексов [1]. Кэш-системы в зависимости от назначения могут значительно различаться, однако основной принцип их реализации – использование двух типов памяти: основной (большой по объему, но медленной) и кэш-памяти (быстрой, но ограниченного объема) [2]. При проектировании кэш-системы определяются ее
основные параметры: количество уровней и размер кэш-памяти, степень ассоциативности, стратегия замещения страниц в кэш-памяти.

Задача определения оптимальной стратегии замещения страниц, ее также называют задачей кэширования, является важнейшей при создании кэш-систем [1]. Суть этой задачи в следующем. Основная память разбита на страницы. Считается, что все страницы пронумерованы, равны по важности и размеру. Кэш-память (или просто кэш) содержит ограниченное количество страниц. На очередном шаге поступает запрос на некоторую страницу. Если эта страница в кэш-памяти уже имеется, достаточно сообщить адрес ее расположения в кэше. Если запрашиваемой страницы нет в кэше, требуется решить, в какое место кэша ее можно записать, предварительно удалив находящуюся там страницу. Алгоритмы решения задачи кэширования называют алгоритмами кэширования или стратегиями замещения. В качестве входных данных для этих алгоритмов выступают размер кэша и трасса запросов – последовательность запрашиваемых страниц. Считается, что трасса запросов целиком неизвестна, обработка запросов выполняется по мере их поступления.

Наиболее известными стратегиями замещения для одноуровневых кэш-систем являются алгоритмы LRU, MRU, LFU, FIFO [2]. Эти алгоритмы детерминированные, в них не предусмотрена сегментация кэш-памяти, они реализуют стратегии замещения страниц, основываясь на истории обработки запросов. Широко используются также вероятностные и адаптивные алгоритмы [3]. Несмотря на то, что к настоящему времени уже разработан целый спектр алгоритмов кэширования, проблема поиска новых подходов к их разработке остается актуальной. Одним из таких подходов, активно развивающихся в последнее время, является гибридизация известных алгоритмов [4, 5].

В настоящей работе предложена автоматная модель стратегии замещения страниц в кэш-памяти. Приведен разработанный на основе этой модели гибридный алгоритм, результативно совмещающий работу стратегий замещения LRU и LFU. Представлены результаты экспериментальных исследований, подтверждающие эффективность предложенного алгоритма в различных условиях, включая «худшие случаи» для каждого из гибридизируемых алгоритмов в отдельности.

Формулировка задачи кэширования

Сформулируем задачу кэширования для одноуровневой кэш-системы в обозначениях, которые далее будут использованы при изложении результатов работы.

Пусть имеется память двух типов: основная и кэш. Вся память разбита на страницы равной длины. Страницы основной памяти пронумерованы. Места для записи страниц в кэш-памяти также пронумерованы и задают адреса расположения страниц в кэше. В основной памяти хранятся d = ∞ страниц. В кэш-память может быть записано только k ≥ 1 страниц. Считается, что все страницы равнозначны между
собой и k значительно меньше d. Имеется трасса запросов s = (s1, s2, ..., si, ..., sn), поступающих в дискретные моменты времени. Каждый запрос si (i = 1, …, n) - это номер вызываемой страницы. Некоторые

страницы могут вызываться многократно. Причем изначально вся последовательность неизвестна. Обработка запросов осуществляется по мере их поступления. При наличии запрашиваемой страницы в кэше (подобная ситуация называется попаданием) результатом выполнения запроса является адрес расположения этой страницы в кэше. В противном случае (эта ситуация называется промахом) требуется указать, по какому адресу можно записать запрашиваемую страницу в кэш. Если в кэше нет свободного места, то промах сопровождается освобождением памяти путем вытеснения (замещения) другой страницы. Решение задачи кэширования - определение эффективной стратегии замещения страниц в кэше. Эффективность стратегии замещения принято оценивать числом попаданий или промахов для трассы запросов σ [1]. Другим критерием эффективности может служить общее время обработки последовательности запросов σ, включающее в себя как время определения наличия запрашиваемой страницы в кэше, так и поиск ее в основной памяти компьютера.

Наиболее распространенными стратегиями замещения являются алгоритмы типа LRU [2]. Данные алгоритмы реализуют следующие стратегии замещения страниц:

Least Recently Used (LRU): алгоритм вытесняет из кэша ту страницу, которая не использовалась дольше всех;
Most Recently Used (MRU): алгоритм вытесняет из кэша последнюю использованную страницу;
Least Frequently Used (LFU): алгоритм подсчитывает, как часто запрашивается та или иная страница, и вытесняет в первую очередь ту страницу, обращения к которой происходят реже всего;
First-in, First-out (FIFO): алгоритм вытесняет страницу, находящуюся в кэше дольше всего, то есть по «возрасту» пребывания страниц в кэше.

В вероятностных алгоритмах при выборе вытесняемой страницы присутствует некая случайность, поэтому определенная страница может быть вытеснена с некоторой вероятностью, зависящей от состояния кэш-системы [1].

Независимо от специфики реализации вход и выход всякого алгоритма кэширования в общем случае можно описать так:

Алгоритм кэширования

Вход: размер кэша k ³ 1, вектор σ = (σ1, σ2, ..., σi) - начальная подпоследовательность последовательности запросов σ = (σ1, σ2, ..., σi, ..., σn) и все предшествующие состояния кэша.

Выход: номер и/или адрес удаляемой из кэша страницы.

Под состоянием кэша здесь понимается множество номеров страниц основной памяти, находящихся в данный момент времени в кэше, и адреса расположения этих страниц в кэше. Кроме того, может учитываться любая дополнительная информация о страницах, находящихся в кэше. Первоначально кэш считается пустым.

Автоматная модель алгоритма кэширования

Для исследования задачи кэширования целесообразно построить математическую модель стратегии замещения страниц. Для этого хорошо подходят математические понятия теории автоматов. Приведем основные сведения из теории автоматов, используя работу [6].

Конечным автоматом (или автоматом Мили) называется система

ℛ = (I, Q, V, δ, λ),                                                                         (1)

где I, Q, V – конечные множества, а функции δ: Q × I → Q и λ: Q × I → V - отображения, заданные на этих множествах. При этом I называется входным алфавитом, V – выходным алфавитом, Q – множеством состояний, δ – функцией переходов, λ – функцией выходов. Автомат называется инициальным, если в Q выделено некоторое состояние q0. Инициальный автомат обозначается через ℛ = (I, Q, V, δ, λ, q0). Считается, что в начальный момент времени автомат ℛ находится в состоянии q0. Если в (1) функция выходов λ зависит только от Q и не зависит от входного алфавита I, то ℛ называется автоматом Мура. Известна теорема, доказывающая, что для любого автомата Мили существует эквивалентный ему автомат
Мура [6]. Благодаря этой теореме, можно определить инициальный автомат как систему ℛ = (I, Q, δ, q0) без указания выходного алфавита и функции выхода.

Опишем модель алгоритма кэширования с помощью инициального автомата Мура. Введем следующие обозначения. Пусть N = {1, 2, ..., d} – множество страниц основной памяти; s = (s1, s2, .., st, ..., sn) – трасса запросов, где st Î N – номер страницы, запрашиваемой в момент времени t = 1, 2, ..., n. Пусть
M = {S : S Í M, |S| £ k} является множеством всех подмножеств множества N, мощность которых не превышает k ³ 1, где k - размер кэша. Полагаем, что каждое такое подмножество S Î M линейно упорядочено, то есть все входящие в S страницы упорядочены в соответствии с некоторым отношением порядка, установленным кэш-системой. Например, такое отношение порядка может быть определено по адресам расположения или по «возрасту» пребывания страниц в кэше. Подмножество S назовем некоторым
(потенциально возможным) состоянием кэша, а M - множеством всех возможных состояний кэш-памяти для заданного k ³ 1. Заметим, что множество M конечно и каждому моменту времени t = 1, 2, ..., n отвечает некоторое состояние St Î M кэш-памяти.

Рассмотрим следующий инициальный автомат Мура:

ℛ = (N, M, δ, q0),                                                                                    (2)

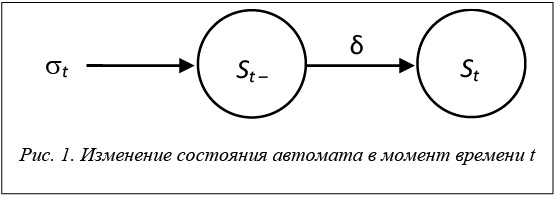
где N = {1, 2, ..., d} – множество страниц основной памяти; M – множество состояний кэш-памяти; q0 – начальное состояние кэша, а функция перехода δ: M × N → M определяет новое состояние кэш-памяти, исходя из текущего состояния кэша и номера запрошенной страницы st. В системе (2) множество N выполняет роль алфавита, множество M - роль множества состояний инициального автомата Мура. Таким образом, система (2) в целом определяет автоматную модель алгоритма кэширования. Функционирование автомата (2) осуществляется на основе трассы запросов s = (s1, s2, .., st, ..., sn). Пусть в момент времени t автомат ℛ находится в состоянии St – 1 Î M и на вход автомата поступает запрос st Î N. Тогда,
согласно функции перехода δ, M × N → M состояние кэш-памяти изменяется и автомат ℛ переходит в положение St Î M (рис. 1). Дискретные моменты времени t = 1, 2, ..., n определяют такты (тактовые моменты), когда автомат может менять свое состояние. Интервалы между тактами могут быть различными. Таким образом, работа автомата зависит не от физического времени, а от номера такта t. Предполагается, что в момент времени 0 автомат находится в начальном состоянии q0 при S0 = Æ. Очевидно, что всякому алгоритму кэширования свойственна своя функция перехода δ: M × N → M.

К настоящему времени разработано немало алгоритмов кэширования со своими достоинствами и недостатками. Многие из них могут быть представлены автоматной моделью (2). Как уже было отмечено, одним из способов улучшения эффективности работы кэш-системы является использование гибридных алгоритмов. Гибридным алгоритмом будем называть два или более алгоритмов кэширования, связанных между собой некоторой функцией переключения f, которая определяет, какой из гибридизируемых алгоритмов будет обрабатывать текущий запрос st. Возможность переключения с одного алгоритма на другой осуществляется через заданное число D тактов на основе накопленной информации об эффективности работы алгоритмов на уже пройденной части трассы запросов. Гибридизация позволяет исключить «худшие случаи» (в смысле эффективности работы) каждого из гибридизируемых алгоритмов и использовать эти алгоритмы в наиболее выгодных для них ситуациях. Определить гибридный алгоритм – прежде всего это задать множество гибридизируемых алгоритмов, значение D и функцию f.

Рассмотрим автоматную модель гибридного алгоритма кэширования с m исходными алгоритмами. Пусть гибридизируемые алгоритмы A1, A2, ..., Am представлены инициальными автоматами Мура

ℛ1 = {N, M, δ1, q0}, ℛ2 = {N, M, δ2, q0}, …, ℛm = {N, M, δm, q0}

с соответствующими им функциями переходов δ1, δ2, …, δm. Если эти автоматы связать с помощью функции переключения f, получим систему 

ℛg = (ℛ1, ℛ2, …, ℛm, f, D),                                                                                                                                        (3)

моделирующую работу гибридного алгоритма, на каждом шаге которого определенным образом, исходя из заданных параметров гибридизации D и f, выбирается подмножество функций переходов из δ1, δ2, …, δm, активных на следующем шаге.

С помощью автоматной модели (3) можно представлять различные комбинации стратегий кэширования и создавать различные гибридные алгоритмы кэширования. Функция переключения f позволяет определить поведение кэш-системы в различных ситуациях. С помощью f возможна тонкая настройка гибридного алгоритма, включая применение элементов адаптации на основе истории обработки трассы запросов s = (s1, s2, .., st, ..., sn). Ведь история обработки может быть чрезвычайно информативной, поскольку длина реальных трасс запросов весьма внушительна, хотя потенциально конечна.

К недостаткам автоматной модели (3) следует отнести невозможность описать стратегии замещения, в которых допускаются кэшируемые объекты различных размеров, и учесть ситуации переполнения кэша при работе с такими объектами.

Гибридный алгоритм кэширования и его программная реализация

Предлагается гибридный алгоритм кэширования Hyb_LRU+LFU, построенный на основе автоматной модели (3). В качестве гибридизируемых алгоритмов A1 и A2 взяты стратегии замещения LRU и LFU.

Функция переключения f в Hyb_LRU+LFU определена следующим образом. Вся исходная трасса запросов s = (s1, s2, .., st, ..., sn) условно разделяется на части (или блоки) Bi размера D ³ 1. Назовем этапом работы гибридного алгоритма обработку двух последовательных частей общим размером 2D. На каждом этапе работы алгоритма Hyb_LRU+LFU обрабатываются части трассы Bi и Bi + 1. Сначала все поступающие запросы части Bi обрабатываются обоими алгоритмами A1 иA2. При этом для каждого из A1 и A2 вычисляется рейтинг кэш-попаданий. Рейтинг кэш-попаданий на Bi вычисляется по формуле

,

где ni - длина обработанной части запросов; ri - число попаданий. Заметим, что в Hyb_LRU+LFU для любого i всегда ni = D. Таким образом, чем больше значение ri, тем выше рейтинг кэш-попаданий рассматриваемой стратегии замещения страниц.

Далее обрабатывается часть Bi + 1, состоящая также из D запросов. Обработка этой части осуществляется тем алгоритмом, который на Bi получил наивысший HR, а значит, и наибольшее значение числа попаданий. Пусть r1, i и r2, i - число попаданий для LRU и LFU на Bi соответственно. При r1, i > r2, i  часть трассы Bi + 1 обрабатывается алгоритмом LRU, иначе - алгоритмом LFU. После этого начинается новый этап работы гибридного алгоритма. Таким образом, переключение гибридного алгоритма с одной стратегии замещения страниц на другую происходит на каждом этапе его работы на основе рейтингов, полученных после работы гибридизируемых алгоритмов на первой половине текущего этапа.

Эффективность гибридизации оценивается числом попаданий гибридного алгоритма на введенной части трассы σ. Поэтому одним из основных результатов работы гибридного алгоритма Hyb_LRU+LFU является значение r – число попаданий на пройденном участке трассы.  

Алгоритм Hyb_LRU+LFU

Вход: d, k, σ, Δ, где d – число страниц основной памяти; k – размер кэша, начальная подпоследовательность трассы запросов σ; n – длина σ; Δ – длина периода адаптации, процедуры LRU (d, k, B) и LFU (d, k, B), результатом работы которых являются числа r1, i и r2, i, вычисленные при обработке участка B алгоритмами LRU и LFU соответственно.

Выход: r – число попаданий.

Пусть

l ← én / Δù

i ← 0

r ← 0

Bi ← [σi × Δ + 1, …, σ (i + 1) × Δ + 1) \\ участок трассы длины Δ

Пока  i < l

                      r1, i ← LRU (d, k, Bi)

                 r2, i ← LFU (d, k, Bi)

                      Если  r1, i > r2, i 

   Тогда

                            r ← r + r1, i

                            r ← r + LRU (d, k, Bi + 1)

   Иначе

                             r ← r + r2, i

       r ← r + LFU (d, k, Bi + 1)

                  i ← i + 2

Вывод r

Конечно, существуют другие способы гибридизации алгоритмов кэширования [4, 5], многие из которых можно представить автоматной моделью (3) с соответствующими параметрами гибридизации Δ и f. Алгоритм Hyb_LRU+LFU также может быть модифицирован. Например, в Hyb_LRU+LFU можно варьировать параметр Δ, а также количество обрабатываемых участков трассы без переключения между стратегиями. Заметим, что увеличение количества частей трассы без переключения уменьшает затраты на вычисление рейтингов, однако при этом уменьшает и уровень адаптации.

Теоретический анализ эффективности алгоритмов кэширования как online-алгоритмов – алгоритмов, обрабатывающих вход по мере поступления, весьма сложен [7]. Поэтому основным методом исследования алгоритмов кэширования на сегодняшний день остается имитационное моделирование, позволяющее оценить эффективность новых алгоритмов в сравнении с известными аналогами.

Для выполнения имитационного моделирования ,разработана программа HR_calculator_LRU_LFU, которая моделирует работу алгоритмов LRU, LFU и реализует гибридный алгоритм Hyb_LRU+LFU. Для эксплуатации программы необходим персональный компьютер типа IBM PC Pentium IV c операционной системой Windows XP/Vista/7.0 и оперативной памятью от 512 Мб. Среда разработки: Visual Studio 2013. На вход программы HR_calculator_LRU_LFU подаются параметры кэш-системы, а на выходе программа выдает значения рейтинга кэш-попаданий для сравниваемых алгоритмов с заданными параметрами моделирования.

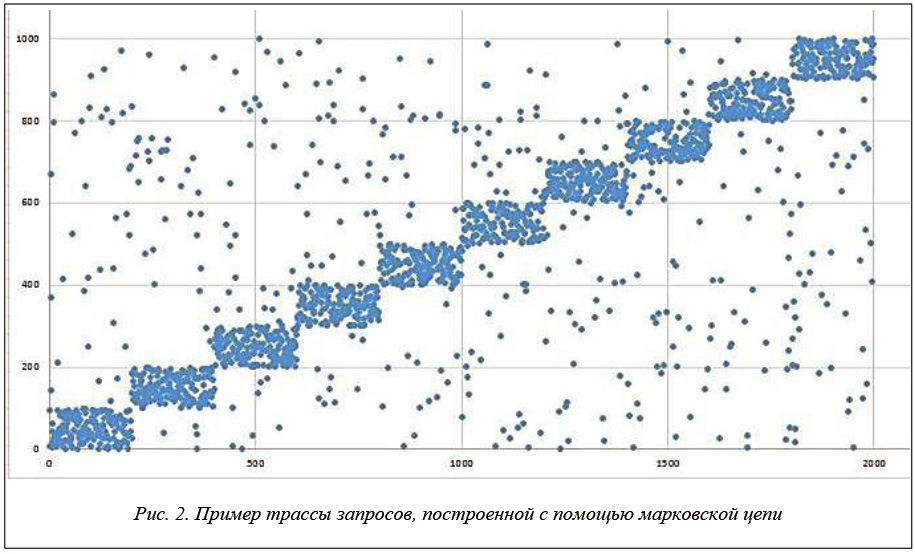
В качестве исходных данных при имитационном моделировании алгоритмов кэширования традиционно используют специально сгенерированные трассы запросов. Метод построения таких трасс был предложен Деннингом и Фейботом и основан на предположении о независимости вероятностей вызова страниц памяти [1, 8]. В методе Деннинга и Фейбота трасса запросов создается с помощью бинарной марковской цепи. В первом состоянии этой цепи генерируется обращение к странице, близкой к текущей, а во втором - к случайной странице. Вероятности переходов между этими двумя состояниями устанавливаются равными Z и 1 - Z (0 ≤ Z ≤ 1) соответственно. В программе HR_calculator_LRU_LFU реализован генератор трасс TrackGenerator по методу Деннинга и Фейбота. В качестве параметров трассы в TrackGenerator рассматриваются: n – длина трассы, d – количество страниц основной памяти, |B| – размер блока трассы, Z – величина, устанавливающая вероятности перехода между состояниями марковской цепи. Трасса запросов, построенная при помощи TrackGenerator, представлена на рисунке 2. Для нее n = 2000, d = 1000, |B| = 200, Z = 0,8. На рисунке по вертикали указаны номера станиц основной памяти, а по горизонтали отмечены номера запросов, то есть тактовые моменты времени поступления запросов в последовательности s.

Экспериментальное исследование гибридного алгоритма

В процессе имитационного моделирования были проведены серии экспериментов. Алгоритмы LRU, LFU и гибридный алгоритм Hyb_LRU+LFU сравнивались по рейтингу попаданий HR. Изменению подвергались 

параметры генератора трассы запросов: Z – величина, устанавливающая вероятности перехода между состояниями марковской цепи, n – длина трассы запросов s;
параметры кэш-системы: d – количество страниц внешней памяти, k – размер кэша; 
параметр D, определяющий период адаптации гибридного алгоритма.

В таблице 1 представлены результаты первой серии экспериментов. Эта серия проводилась при n = 1000–40000, k = 100 и D = 200. В этой серии использовались трассы, сконструированные для отражения «худшего случая» (с точки зрения эффективности работы) алгоритма LRU.

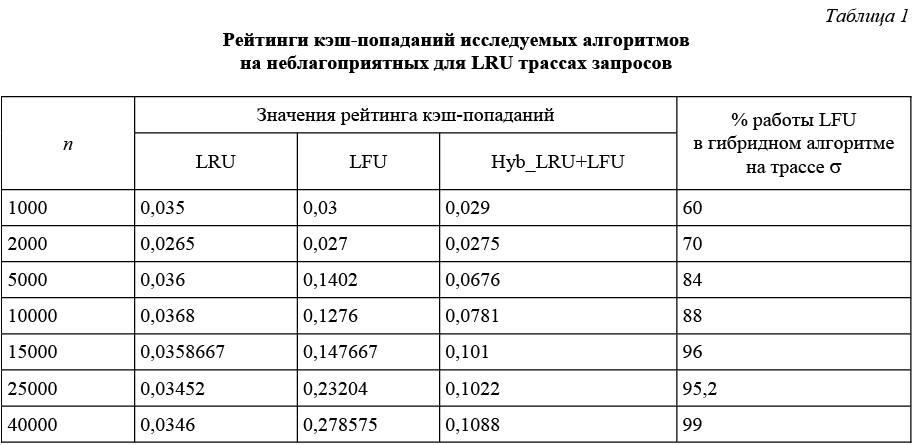
Из таблицы 1 видно, что на трассах, отвечающих «худшему случаю» для LRU, алгоритмы LFU и Hyb_LRU+LFU работают эффективнее LRU, при этом гибридный алгоритм Hyb_LRU+LFU на более длинных трассах успешно адаптируется и переключается чаще всего на LFU.

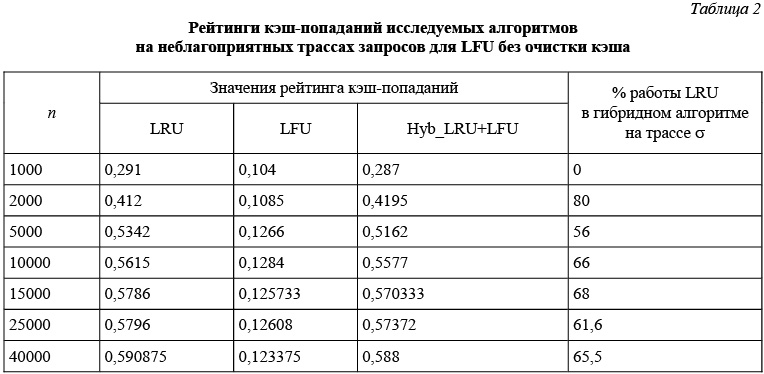
Вторая серия экспериментов проводилась при n от 1000 до 40000, k = 100 и D = 200. В этой серии использовались трассы запросов, построенные с помощью генератора TrackGenerator для Z = 0,8. В самом алгоритме LFU при обработке этих трасс не выполнялась операция очистки кэша, что в ряде случаев приводило к «загрязнению» кэша и неэффективной работе LFU. Результаты данной серии экспериментов, приведенные в таблице 2, подтверждают неэффективность алгоритма LFU без очистки кэша. Особенно это наблюдается на длинных трассах. Однако в алгоритме Hyb_LRU+LFU на трассе запросов длиной n = 40000 даже небольшое переключение с LFU на альтернативный алгоритм LRU способствует очистке кэша и повышает эффективность работы LFU с рейтинга 0,123375 до 0,588.

Третья серия экспериментов проводилась с переменным параметром D при n = 1000, k = 100, d = 20000. В этой серии использовались трассы, сгенерированные с помощью TrackGenerator для Z = 0,8. Цель данной серии экспериментов - установить, имеет ли место зависимость значения рейтинга
кэш-попаданий гибридного алгоритма от величины периода адаптации D. В алгоритме LFU была предусмотрена очистка кэша от «загрязнения». Из результатов данной серии экспериментов, приведенных в таблице 3, следует, что для эффективной работы гибридного алгоритма параметр D необходимо выбирать равным 2-4 размерам кэша. Уменьшение D нецелесообразно, поскольку это влечет увеличение вычислительных затрат, а увеличение D приводит к тому, что алгоритм не успевает адаптироваться к изменениям трассы.

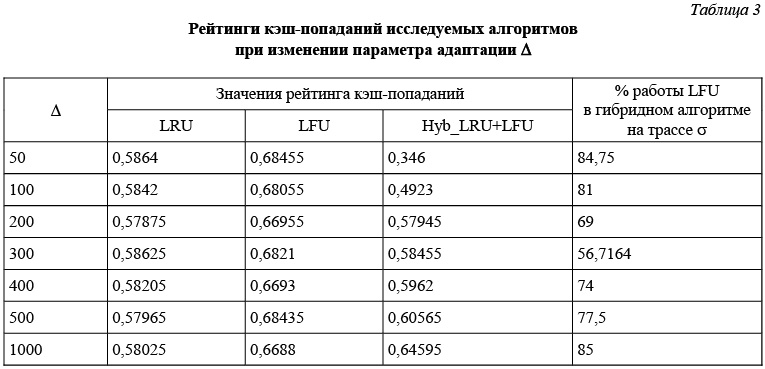
В таблице 4 представлены результаты четвертой серии экспериментов. Эта серия проводилась с переменным параметром Z при n = 1000, k = 100, d = 20000, D = 200. В этой серии использовались трассы, сгенерированные с помощью TrackGenerator при различных значениях Z. Цель данной серии экспериментов - исследование зависимости эффективности работы исследуемых алгоритмов от значения Z.

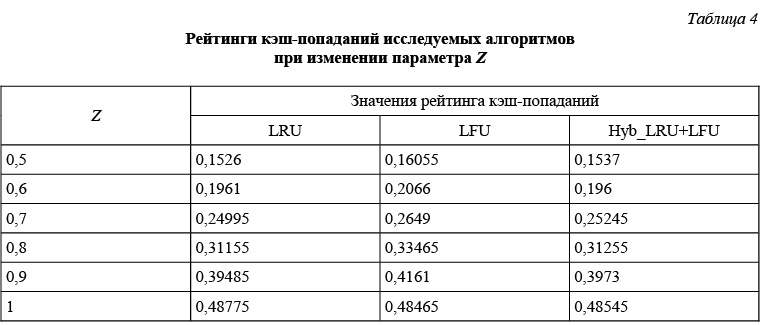
Из таблицы 4 видно, что увеличение значения Z (степени предсказуемости «будущего» от «настоящего» и «прошлого»), то есть доли страниц, номера которых зависят от ранее вызванных страниц, увеличивает рейтинги попаданий всех исследуемых алгоритмов кэширования. Это объясняется тем, что рассматриваемые алгоритмы LRU, LFU и Hyb_LRU+LFU реализуют стратегии замещения страниц, основываясь исключительно на истории обработки запросов.

В целом по результатам экспериментальных исследований можно сделать следующие выводы. Предложенный гибридный алгоритм Hyb_LRU+LFU эффективнее каждого из алгоритмов LRU, LFU в отдельности как на трассах запросов, неблагоприятных для этих алгоритмов, так и на трассах, построенных генератором TrackGenerator. Эффективность алгоритма Hyb_LRU+LFU может быть улучшена путем подбора параметра D на основе информации о реальных трассах запросов.

К настоящему времени разработано много алгоритмов кэширования со своими достоинствами и недостатками. Одним из подходов повышения эффективности работы современных кэш-систем является использование гибридных алгоритмов. Гибридизация позволяет нивелировать «худшие случаи» для каждого из гибридизируемых алгоритмов и использовать эти алгоритмы в наиболее выгодных для них ситуациях. Представленная в статье детерминированная автоматная модель гибридизации может служить формальной основой для разработки новых гибридных алгоритмов кэширования. Перспективны дальнейшие исследования по разработке новых математических моделей, включая вероятностные и интеллектуальные системы автоматов, и новых подходов гибридизации алгоритмов кэширования.

Литература

1. Аль-Згуль М.Б. Гибридные алгоритмы в системах кэширования объектов // Вестн. ДГТУ. 2008.
№ 4. С. 403-411.

2. Аль-Згуль М.Б. Гибридные алгоритмы кэширования для систем обработки и хранения информации: дис… канд. техн. наук. Р-н-Д: Донской гос. тех. ун-т, 2009. 150 с.

3. Болотов П.В. Принципы работы кэш-памяти. 2007. URL:  http://alasir.com/articles/cache_principles/index_rus.html (дата обращения: 19.05.2016).

4. Жуков А.И., Гранков М.В. Методика экспериментального исследования эффективности систем кэширования информации // Труды II Междунар. семинара; [под общ. ред. P.A. Недорфа]. Изд-во Донского гос. техн. ун-та, 2011. С. 130-132.

5. Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы. Построение и анализ. М.: Вильямс, 2013. 1328 с.

6. Кузнецов О.П. Дискретная математика для инженера. М.: Лань, 2007. 400 с.

7. Рассел Д. Алгоритмы кэширования. VSD, 2013. 90 с.

8. Latha Shanmuga Vadivu S.L.S., Rajaram M. Optimization of web caching and response time in semantic based multiple web search engine. European Journ. of Sc. Research, 2011, vol. 56, no. 2, pp. 244-255.