Работа посвящена разработке методики машинной атрибуции текстов. Методика может быть использована для поиска текстов необходимого жанра и стиля, а также установления авторства и оценки юзабилити текста. Предполагается уделить особое внимание проблеме выявления текстов научной направленности среди большого массива разнородной информации.

Решение подобных задач требует отработки междисциплинарных взаимодействий в науке. Законы построения текста, определяемые спецификой гуманитарного знания, должны также соответствовать требованиям существования численного выражения и математического формализма.

Статистические исследования связаны с исследованием количественных характеристик текстов. Исследования количественных параметров текстов проводятся давно, и первым теоретическим результатом в области статистических исследований текста считается эмпирический закон Ципфа [1]. Количественным параметром при этом является частота встречаемости слов в тексте.

Методы математической статистики в основном применялись в работах, посвященных установлению авторства [2–7]. Встречаются и примеры применения статистических методов к более широкому спектру задач [8].

Возможности автоматической жанровой классификации текстов также рассматривались, например,
в исследованиях, связанных со сжатием текста при помощи алгоритмов архивации [9].

В работах [10–14] использовались методы частотного анализа и модель случайных блужданий.
С их помощью был получен ряд параметров, которые можно использовать как атрибуты текста. Эти параметры удовлетворяют требованиям объективности и возможности математической обработки результатов, выдвинутым авторами в работе [15].

В настоящей работе указанные параметры были использованы в качестве переменных в дискриминантном и факторном анализе.

Приведем перечень параметров, используемых для исследования.

1. Величина статистики [10, 14].

Была рассчитана вероятность появления каждого из возможных сочетаний гласных букв, взятых
по три, как произведение вероятностей появления каждой буквы, входящей в данное сочетание:

p_i = p_i1 p_{i 2} p_i3,

где p_i – вероятность появления данного сочетания;p_i1, p_i2, p_i3 – вероятности появления 1, 2 и 3-й букв в i-м сочетании.

Это теоретическое распределение, имеющее место в случае, когда все буквы не зависят друг от друга. В таком случае текст будет представлять собой полностью хаотическую систему. В качестве критерия оценки отличия наблюдаемого распределения от теоретического использовался стандартный критерий Пирсона :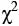

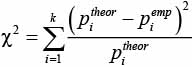
где p_i^theor вычислено по формуле как произведение вероятностей; p_i^emp получено из реального текста с помощью специально разработанной программы.

2. Коэффициент пропорциональности из закона больших чисел (c) [12].

Для каждого текста были посчитаны стандартные отклонения величины 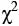по фрагментам этого текста различной длины:

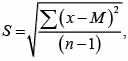
где x – значение признака у каждого объекта в группе; M – среднее арифметическое признака; n – число вариантов выборки.

Согласно закону больших чисел, величина стандартного отклонения 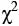при увеличении количества гласных букв в тексте будет асимптотически стремиться к нулю согласно

где S – величина стандартного отклонения; N – количество гласных во фрагменте текста; c – эмпирическая константа.

Если значения c будут разными для разных текстов, то ее можно рассматривать как атрибут конкретного текста.

3. Коэффициент диффузии (D) и относительная поправка к закону Эйнштейна (RC) [11].

В этой модели текст рассматривается как цепочка случайных событий – появлений очередной гласной буквы. Основное допущение модели состоит в том, что процесс полагается полностью случайным, то есть появление новой гласной не зависит от предыдущей. Любое случайное блуждание может быть описано законом Эйнштейна, который для двумерного случая выглядит следующим образом:

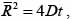
где R – смещение; D – некий коэффициент пропорциональности, аналогичный коэффициенту диффузии для физической системы; t – время. Коэффициент D для удобства будем называть коэффициентом диффузии, а время t соответствует порядковому номеру буквы от начала текста.

Смещение рассчитывается после определенного числа скачков. С точки зрения физического представления нельзя точно определить траекторию случайного блуждания, так как каждый скачок происходит в случайном направлении. Поэтому возникает необходимость в усреднении смещения по множеству случайных процессов. В данном случае ему соответствует множество фрагментов исследуемого текста.

В рассматриваемой модели движение происходит в некоторой плоскости, каждой букве соответствует свой вектор. Проекции вектора на оси ОХ и ОУ рассматриваются как смещение в направлении соответствующей оси. Каждое смещение по осям ОХ и ОУ вычисляется как сумма предыдущего смещения и длины нового скачка. Длина вектора есть величина, обратно пропорциональная частоте появления буквы. Такое значение длины вектора было выбрано для того, чтобы исключить дрейф в сторону букв, встречающихся чаще, чем другие. Углы для каждой буквы выбраны следующим образом: единичная окружность поделена на девять углов по 40º и повернута на 5º по часовой стрелке, чтобы направление вектора не совпало с направлением оси, иначе приращение функции по одной из осей было бы равно нулю.

Для некоторых текстов наблюдалось очевидное отклонение зависимости <R²(t)> от линейного закона. Для описания степени отклонения введена относительная поправка к закону Эйнштейна (RC).

4. Год создания текста.

Для русскоязычного текста временем создания считаем год его написания автором, для переводного – год перевода на русский язык [15].

5. Процент сжатия текста (%).

Под процентом сжатия текста понимаем процент сжатия файла при его архивировании архиватором WinRAR [11].

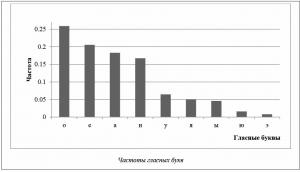
63. Частоты появления в тексте отдельных гласных букв (ω _i).

Всего рассматривалось 9 гласных букв, «е» и «ё» считались за одну букву [15].

На рисунке представлена диаграмма частот гласных букв в порядке убывания, полученная усреднением приблизительно по 1 500 текстов различных жанров. Из диаграммы видно наличие двух групп гласных букв – часто встречающиеся (о, е, а, и) и редко встречающиеся (у, я, ы, ю, э).

Сначала оценивалась степень разделения текстов по жанрам с использованием ранее перечисленных параметров методом дискриминантного анализа [16].

В качестве материала для исследования были взяты по 35 текстов из трех групп – художественная проза, научные и административные тексты. На следующем этапе количество текстов было увеличено до 100. В таблице 1 представлены результаты дискриминантного анализа для обоих случаев.

Таблица 1

Сравнение процента распознавания (распределения текстов по группам)

Из таблицы 1 видно, что максимальный процент распознавания был получен в случае использования в качестве переменных всех 15 параметров. При использовании только рассчитанных параметров процент остается также достаточно высоким. Использование в качестве переменных только частот гласных букв снижает процент правильного распознавания.

Также из таблицы 1 следует, что при увеличении числа текстов в 3 раза процент распознавания практически не изменился (изменения в пределах погрешности), то есть зависимость процента правильного распознавания от количества текстов не обнаружена. Следовательно, различия между группами текстов являются системными и определяются особенностями текстов, входящих в группы, а не случайными эффектами.

Сравнивая результаты, можно заметить, что процент распознавания по параметрам существенно выше, чем по частотам. Частоты букв определяются в основном лексикой. Рассчитанные параметры, по-видимому, в гораздо большей степени определяются структурой текста. То есть все параметры можно разделить на лексические (общеязыковые) и стилистические (структурные). К первым относятся частоты букв, ко вторым – параметры 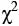, c, D, RC, процент и год создания.

Тексты из разных областей отличаются по набору слов, но в большей степени они отличаются
по порядку слов, то есть структурно, а не лексически.

Таким образом, получены разные наборы параметров. В случае 105 текстов наиболее значимыми для классификации оказались коэффициент диффузии (D), год создания, процент сжатия, частоты букв «а», «и», «ы», «о», «э», «ю». Для случая 300 текстов наиболее значимыми оказались процент сжатия, величина статистики 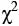, год создания, относительная поправка к закону Эйнштейна (RC), коэффициент пропорциональности (c), частоты букв «и», «э», «а», «е», «я», «ю».

Следующей задачей исследования стало уменьшение количества параметров, используемых для классификации текстов, при сохранении качества разделения, то есть нахождение набора параметров, который будет одновременно и компактным, и информативным.

С этой целью были применены статистические методы факторного и дискриминантного анализа. В результате найден набор, включающий в себя только 5 параметров из рассмотренных 15. В этот набор вошли параметры D, 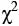, % и частоты встречаемости букв «о» и «э»: ωо, ωэ, то есть частоты самой распространенной и самой редкой буквы.

Далее был проведен дискриминантный анализ с наиболее компактным набором параметров (табл. 2). Процент правильного распознавания стал немного хуже, но несущественно по сравнению с результатом анализа с использованием всех рассматриваемых параметров.

Таблица 2

Результат дискриминантного анализа с использованием набора параметров D, 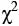, %, ω_о, ω_э

Проведем сравнение средних значений отобранных параметров для научных текстов и текстов другой направленности (табл. 3).

Таблица 3

Результаты сравнения средних значений параметров D, 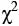, %, ω_о, ω_э
для текстов различной направленности

Как видно из таблицы, значения почти всех выбранных параметров для научных текстов занимают промежуточное положение среди аналогичных параметров для других текстов. Исключение составляет только частота встречаемости буквы «э», которая в научных текстах оказывается в среднем больше, чем во всех прочих текстах. При этом средние значения всех параметров для научных текстов статистически значимо не отличаются от таковых для прочих параметров. Поэтому выявить научные тексты по значениям каких-то отдельно взятых параметров затруднительно. Для этого необходимо использовать решающие правила дискриминантного анализа.

В процессе исследований не выявлено значимой зависимости процента правильного распознавания от количества текстов. Следовательно, различия между группами текстов являются систематическими и определяются особенностями текстов, входящих в группы, а не случайными эффектами.

Набор используемых параметров удалось сократить с 15 до 5 практически без потери качества классификации текстов. Наиболее компактным и информативным оказался следующий набор параметров: коэффициент диффузии (D), величина статистики 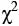, процент сжатия, частоты букв «э», «о» (ω _э, ω_о). В набор параметров вошли частоты самой часто встречающейся гласной буквы «о» и самой редко встречающейся «э».

Полученный набор параметров дает хорошую достоверность для выявления и отбора научных текстов (86 %) по решающим правилам линейного дискриминантного анализа, при этом выявить научные тексты по значениям отдельных параметров из полученного набора оказывается затруднительным.

Литература

1. Wentian Li. Random texts exhibit Zipf’s-Law-Like word frequency distribution. Santa Fe Inst. Publ., 1991, pp. 1–8.

2. Андреев Н.Е. Статистические и комбинаторные методы в теоретической и прикладной лингвистике. Л.: Наука, 1967. 403 с.

3. Головин Б.Н. Язык и статистика. URL: http://bookre.org/reader?file=1214147&pg=2 (дата обращения: 30.04.2018).

4. Гришунин А.Л. Исследовательские аспекты текстологии. М.: Наследие, 1998. 416 с.

5. Журавлев А.П. Опыт вероятностно-статистического изучения стилевых различий. В кн.: Язык
и общество. Саратов, 1967.

6. Каджазнули Л.К. Статистический анализ индивидуального стиля: автореф. дис… канд. филол. наук. Тбилиси, 1977. 24 с.

7. Хмелев Д.В. Распознавание автора текста с использованием цепей А.А. Маркова // Вестн. Московск.ун-та: Филология. М., 2000. № 2. С. 115–127.

8. Орлов Ю.Н., Осминин К.П. Методы статистического анализа литературных текстов; [под ред. Г.Г. Малинецкого]. М.: Либроком, 2012. 300 с.

9. Селиванова И.В., Рябко Б.Я., Гуськов А.Е. Классификация посредством компрессии: применение методов теории информации для определения тематики научных текстов // НТИ: Информационные процессы и системы. 2017. № 6. C. 8–15.

10. Амиева А.М., Крамаренко А.А., Филимонов В.В., Живодеров А.А. Машинная атрибуция русскоязычных текстов: обзор методов // Новые информационные технологии в образовании и науке (НИТО-2017): матер. X Междунар. науч.-практич. конф. Екатеринбург: РГППУ, 2017. С. 371–375.

11. Крамаренко А.А., Филимонов В.В., Живодеров А.А., Амиева А.М. Применение модели случайных блужданий для описания русскоязычных текстов // Информация: передача, обработка, восприятие: матер. Междунар. науч.-практич. конф. Екатеринбург: Изд-во УрФУ. 2017. С. 138–164.

12. Филимонов В.В., Амиева А.М., Живодеров А.А., Крамаренко А.А. Атрибутирование русскоязычных текстов с использованием закона больших чисел // Информация: передача, обработка, восприятие: матер. Междунар. науч.-практич. конф. Екатеринбург: Изд-во УрФУ, 2017. С. 10–18.

13. Филимонов В.В., Амиева А.М., Сергеев А.П. Кластеризация русскоязычных текстов с применением статистики χ² // Информация: передача, обработка, восприятие: матер. Междунар. науч.-практич. конф. Екатеринбург: Изд-во УрФУ, 2016. С. 164–174.

14. Филимонов В.В., Живодеров А.А., Горбич Л.Г. Эмоциональная экспрессия и порядок в письменной речи. // Изв. УрФУ: Проблемы образования, науки и культуры. 2012. № 3. С. 313–319.

15. Амиева А.М., Филимонов В.В., Живодеров А.А. Применение дискриминантного анализа к классификации русскоязычных текстов // Информационные технологии, телекоммуникация и системы контроля: матер. IV Междунар конф. М.: Эдитус, 2017. С. 65–71.

16. Filimonov V.V, Zhivodyorov A.A., Amieva A.M., Pykhova E.D. A sufficient set of statistical parameters for the classification of Russian-language texts. Proc. V Intern Young Researchers' Conf. (PTI.2018). 2018. DOI: 10.1063/1.5055095.