В настоящее время наблюдаются бурное развитие суперкомпьютерных технологий и повышение производительности вычислительных систем. Для суперкомпьютеров петафлопсного диапазона производительности обычный размер расчетной сетки составляет сотни миллионов ячеек [1], и требования постоянно повышаются. Ожидается, что самый мощный на сегодняшний день суперкомпьютер Sunway TaihuLight [2] с пиковой производительностью более 100 PFLOPS уже в этом году будет потеснен сразу несколькими новыми машинами, в первую очередь, суперкомпьютером Summit от IBM, оснащенным универсальными процессорами Power9 и графическими ускорителями NVidia с архитектурой Volta.
Одновременно с наращиванием вычислительной мощности суперкомпьютеров возникают вопросы эффективности их применения. Проводятся исследования и ведутся работы по повышению эффективности систем обмена данными между вычислительными узлами [3], по развитию систем планирования заданий на суперкомпьютерных ресурсах [4], по повышению эффективности работы суперкомпьютеров с системами хранения данных [5], по развитию технологий управления расчетными сетками и равномерного распределения вычислений на суперкомпьютерном кластере [6, 7]. Самым низкоуровневым направлением создания высокопроизводительного параллельного кода является оптимизация на уровне операций. Поддержка микропроцессорами векторных вычислений открывает широкие возможности для оптимизации кода [8], так как использование векторных инструкций теоретически способно кратно увеличить производительность приложений. Однако при выполнении векторизации программного кода необходимо учитывать факторы, которые могут негативно повлиять на итоговую производительность.
В данной статье рассматривается проблема векторизации кода для процессоров Intel Xeon Phi x200 Knights Landing (KNL) применительно к гнезду циклов со сложным управлением и переменным числом итераций внутреннего цикла.
Микропроцессор KNL и набор инструкций AVX-512
Семейство микропроцессоров KNL [9] – это второе поколение линейки Intel Xeon Phi, представленное в 2016 году. Каждый процессор содержит до 36 активных тайлов, в состав каждого из которых входят два ядра и L2 кэш размером 1 MB, являющийся общим для данных двух ядер. Каждое ядро содержит устройство векторной обработки (VPU, Vector Processing Unit), поддерживающее 512-битные векторные инструкции, и кэш первого уровня (L1) размером 64 KB, разделенный на равные по размеру кэш инструкций и кэш данных. Каждое ядро поддерживает четыре потока, что дает суммарно 288 логических процессоров на сокет. Хотя частота каждого ядра KNL ниже, чем у серверных процессоров Intel Xeon, большое количество потоков исполнения и наличие 512-битных векторных инструкций обеспечивает внушительную пиковую производительность, превышающую 6 TFLOPS на операциях с одинарной точностью и 3 TFLOPS на операциях с двойной точностью.
Набор инструкций AVX-512 представляет собой 512-битное расширение 256-битных AVX инструкций из набора команд Intel x86 [10], поддерживаемое в семействах микропроцессоров Intel Xeon Phi KNL и Intel Xeon Skylake. В микропроцессорах KNL поддерживаются следующие подмножества инструкций AVX-512: AVX-512F (Foundation) – основной набор векторных инструкций с поддержкой маскирования, AVX-512PF (PreFetch) – инструкции предварительной подкачки данных из памяти, AVX-512ER (Exponential and Reciprocal) – команды для вычисления экспоненты и обратных значений, AVX-512CD (Conflict Detection) – инструкции для определения совпадения элементов вектора друг с другом, помогающие в определении конфликтов по доступу в память.
Для поддержки выборочного применения операций над упакованными данными к конкретным элементам вектора используются маски. Большинство инструкций из набора AVX-512 могут использовать специальные регистры масок. Всего таких регистров 8 (k0–k7). Длина каждой маски составляет 64 бита. Маски k0–k7 используются в командах для осуществления условной операции над элементами упакованных данных (если соответствующий бит выставлен в 1, то операция выполняется, а точнее, результат операции записывается в соответствующий элемент вектора назначения) или для слияния элементов данных в регистр назначения. Также маски могут использоваться для выборочного чтения и записи в память элементов векторов, для аккумулирования результатов логических операций над элементами векторов.
Можно выделить несколько групп операций AVX-512. Упакованные операции с одним операндом zmm (512-битный вектор) и одним результатом zmm (получение абсолютного значения, извлечение корня, округление, операции сдвигов), упакованные операции с двумя операндами zmm и одним результатом zmm (операции поэлементного сложения, вычитания, умножения, деления, сдвига на переменное количество разрядов), упакованные операции с двумя операндами zmm и результатом маской (поэлементное сравнение двух векторов), операции конвертации, предназначенные для преобразования элементов вектора из одного формата в другой (cvt, pack), упакованные комбинированные операции (поэлементное вычисление значений вида ), операции перестановок, операции пересылок (в частности, операции пересылки элементов данных, расположенных не последовательно, а с произвольными смещениями от заданного базового адреса в памяти, а также операции пересылки с дублированием элементов), операции предварительной подкачки данных и другие операции с более сложной логикой, среди которых определение класса вещественного числа, реализация логических функций от трех аргументов, операции определения конфликтов и другие.
Для упрощения векторизации исходного кода для компилятора icc разработаны специальные функции-интринсики [11, 12], определенные в заголовочном файле immintrin.h. Они покрывают не все инструкции AVX-512, однако избавляют от необходимости вручную писать ассемблерный код и позволяют использовать встроенные типы данных для 512-битных векторов (__m512, __m512i, __m512d). Некоторые интринсики соответствуют не отдельной команде, а целой последовательности, например, для операции сложения всех элементов вектора. Из множества интринсиков можно выделить следующие группы функций, схожие по структуре. Функции swizzle, shuffle и permute осуществляют перестановку элементов вектора и раскрываются в последовательность операций, в которой присутствуют операция shuf и пересылка по маске. Для большего числа операций AVX-512 реализованы соответствующие инстринсики, раскрывающиеся в одну конкретную операцию. Среди них арифметические операции, побитовые операции, операции чтения из памяти и записи в память, операции конвертации, слияние двух векторов, нахождение обратных значений, получение минимума и максимума из двух значений, операции сравнения, операции с масками, комбинированные операции и другие. Некоторые инстринсики, особенно предназначенные для выполнения упакованных трансцендентных операций, раскрываются просто в вызов библиотечной функции (например, _mm512_log_ps, _mm512_hypot_ps, тригонометрические функции).
Подходы к векторизации циклов с помощью инструкций AVX-512
Векторизации циклов с помощью инструкций AVX-512 для процессоров KNL и Skylake уделяется достаточно много внимания. Можно отметить работы по векторизации быстрой сортировки [13], алгоритма построения множества Мандельброта [14], операций над разреженными матрицами [15], быстрого преобразования Фурье [16], циклов с маловероятными ветвями исполнения [17]. В данном разделе приведем краткое описание основных видов контекста для векторизации, большее разнообразие контекстов можно найти в [18, 19].
Самый простой вид циклов для векторизации – плоские циклы. Это циклы, в которых отсутствуют побочные эффекты и зависимости между итерациями, то есть все операции могут выполняться параллельно. Также все обращения к элементам всех массивов выполняются по одному и тому же индексу (в идеале на i-й итерации цикла возможны только обращения вида a[i]). Примером может служить поэлементное сложение двух массивов. Такие циклы хорошо подходят для векторизации, и при выполнении необходимых условий по выравниванию компилятор применяет векторизацию. Если количество итераций плоского цикла не делится нацело на длину вектора, то лишние итерации нужно выполнять отдельно в невекторизованном виде либо с использованием масочных операций.
При добавлении в плоский цикл команд ветвления (оператор if) компилятор icc также без труда справляется с векторизацией, используя масочные операции и операции слияния по условию. Сложнее дело обстоит, если внутри векторизуемого цикла появляется другой цикл с непостоянным количеством итераций. Такие конструкции встречаются, например, в реализации задачи Римана о распаде произвольного разрыва [20], и они не поддаются автоматической векторизации. Однако в случае независимости итераций вложенного цикла друг от друга охватывающий цикл все же можно векторизовать вручную, заменив все операции на векторные аналоги, использующие в качестве операнда вектор предикатов продолжения выполнения каждой из объединенной итерации исходного вложенного цикла (подробнее данный подход будет рассмотрен в следующем разделе).
В случае наличия в векторизуемом цикле маловероятных ветвей исполнения можно выполнить расщепление цикла по условию, получив два цикла, в первом из которых будет сохраняться только условие ухода на маловероятную ветку, во второй попадет ее реализация. После преобразования первый цикл, избавившись от маловероятного кода, может быть эффективно векторизован [17]. Другие эквивалентные преобразования циклов, в результате которых цикл может быть приведен к виду, пригодному для автоматической векторизации, можно найти в фундаментальных трудах [21, 22].
Важным и трудно поддающимся векторизации контекстом является свертка над массивом. Сверткой называется преобразование структуры данных к единственному значению при помощи последовательного применения заданной функции с сохранением промежуточного результата в аккумуляторе; промежуточный результат также подается на вход следующему вызову данной функции [23]. Простейшим примером свертки является вычисление суммы элементов массива. Данный контекст легко векторизуется, так как является обычным шаблоном для оптимизирующего компилятора, к тому же обладает коммутативностью (элементы массива можно складывать в любом порядке). В общем случае для векторизации свертки с межитерационной зависимостью придется выполнить раскрутку цикла (дублирование тела цикла) на необходимое количество итераций.
Векторизация гнезда циклов на примере реализации сортировки Шелла
Сортировка Шелла [24] является усовершенствованным вариантом сортировки вставками, предложенным в 1959 году Дональдом Л. Шеллом. В отличие от сортировки вставками, при которой элемент массива каждый раз перемещается только на одну позицию, что приводит к квадратичной сложности алгоритма, сортировка Шелла позволяет сравнивать и менять местами элементы, находящиеся на большом расстоянии друг от друга, выполняя так называемые грубые проходы сортировки. В начале работы алгоритма выбирается некоторый стартовый шаг прохода k0, после чего выполняется сортировка подмассивов с индексами {j | j = j 0 + ik0} для всех j0 < k0. Далее аналогичная процедура выполняется со следующим шагом прохода k1 < k0. Количество предварительных грубых проходов может быть произвольным. В конце концов выполняется финальный проход с шагом, равным единице, являющийся обычной сортировкой вставками. Среднее время работы алгоритма зависит от выбора шагов проходов. Одной из наиболее эффективных последовательностей шагов на сегодняшний день является эмпирическая последовательность Марцина Циура [25, 26]. Будем рассматривать простую последовательность шагов с начальным шагом, равным половине размера массива с уменьшением шага следующего прохода в два раза (такая последовательность первоначально использовалась Шеллом). Тогда простая реализация сортировки Шелла на языке программирования C может выглядеть следующим образом:
void shell_sort(float *m, int n)
{
int i, j, k;
for (k = n / 2; k > 0; k /= 2) // внешний цикл
{
for (i = k; i < n; i++) // промежуточный цикл
{
float t = m[i];
for (j = i; j >= k; j -= k) // внутренний цикл
{
if (t < m[j - k])
{
m[j] = m[j - k];
}
else
{
break ;
}
}
m[j] = t;
}
}
}
В данной реализации внешний цикл по переменной k соответствует выполнению проходов для всех шагов, начиная от половины длины массива и заканчивая единицей. Гнездо, состоящее из двух внутренних циклов, реализует проход с фиксированным шагом. Самый вложенный цикл (цикл с счетчиком j, будем называть его просто внутренним) выполняет сортировку одного подмассива, состоящего из элементов массива, с расстоянием k между соседними элементами.
Внутренний цикл не может быть векторизован без выполнения дополнительных модификаций кода, так как между записью элемента m[j] и чтением элемента m[j – k] существует межитерационная зависимость по данным. Однако, можно заметить, что две итерации среднего по вложенности цикла (цикла со счетчиком i, будем называть его промежуточным) с номерами i1 и i2 не конфликтуют по данным и поэтому могут быть выполнены параллельно при выполнении условия |i1 – i2| < k.
На рисунке 1 сверху разными цветами изображены четыре подмассива, для которых выполняется сортировка, что иллюстрирует параллельное выполнение четырех последовательных итераций промежуточного цикла. Снизу показано аналогичное действие, однако элементы массива объединяются в векторы по четыре элемента в каждом. Сравнение и пересылка данных в этом случае выполняются с использованием векторных операций. Так как векторы zmm имеют длину 512 бит, они могут объединять 16 элементов типа float или 8 элементов типа double. Так как в статье рассматривается массив с элементами типа float, будем объединять по 16 итераций промежуточного цикла для больших шагов k ≥ 16. При объединении итераций может возникнуть необходимость выполнения невекторизованных последних итераций цикла. Они возникают, когда общее количество итераций цикла не кратно 16. Довыполнение цикла, как правило, слабо влияет на производительность при условии большого количества итераций цикла. Для внутреннего цикла гнезда неизвестно количество итераций, поэтому для векторизации понадобится использование маскированных векторных операций.
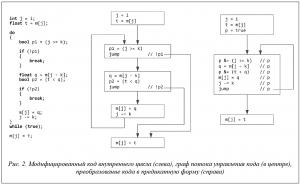
Для подготовки к векторизации выполним преобразование кода внутреннего цикла. Преобразуем цикл в форму do while вместо for, а выходы из цикла явно обозначим командами break. Введем булевые переменные для получения условий выхода таким образом, чтобы выходы из цикла осуществлялись под негативными предикатами (см. рис. 2, слева). В полученном модифицированном коде можно отметить, что выполнение каждой строчки в теле цикла возможно только при условии истинности всех полученных предикатов (p1 и p2). На рисунке 2 в центре приведен граф потока управления полученного участка кода. Видно, что управление довольно разветвленное, так как цикл, кроме обратной дуги, содержит два выхода, расположенных в середине тела. Можно значительно упростить логику выполнения тела цикла, использовав предикатный режим выполнения инструкций [27]. Наличие предикатного режима исполнения операций позволяет избежать создания ненужных операций передачи управления путем планирования в одном линейном участке команд под различными предикатами. Предикатный режим исполнения поддержан в таких архитектурах, как ARM [28] или «Эльбрус» [29]. В архитектуре x86 нет предикатного режима исполнения инструкций в полном смысле, однако в случае набора инструкций AVX-512 можно утверждать, что такой режим есть, так как для большинства векторных инструкций специальный масочный аргумент играет роль вектора предикатов. Преобразуем построенный граф потока управления, заменив суперблок тела цикла на гиперблок с одним прямым выходом и одной обратной дугой и содержащий предикатный код (рис. 2, справа). При этом заметим, что можно использовать один и тот же предикат для всех инструкций в теле цикла, дополняя данный предикат по мере накопления условий (с помощью операции p &= cond).
Полученный гиперблок с телом цикла содержит операции целочисленного сравнения, чтения вещественного значения из массива по индексу, вещественного сравнения, сохранения вещественного значения в память по индексу, целочисленного вычитания. Кроме того, в цикле присутствуют операции с булевыми переменными. Все указанные операции представлены векторными аналогами в наборе инструкций AVX-512 и реализованы в виде функций-интринсиков. Таким образом, можно выполнить векторизацию цикла, заменив скалярные операции на соответствующие векторные.
void shell_sort_step_big_i16(float *m, int n, int k, int i)
{
__m512i ind_i = _mm512_set1_epi32(i);
__m512i ind_j = _mm512_add_epi32(ind_i, ind_straight);
__m512 t = _mm512_i32gather_ps(ind_j, m, _MM_SCALE_4);
__mmask16 mask = 0xFFFF;
__m512i ind_jk;
__m512 q;
do
{
mask = mask & _mm512_mask_cmp_epi32_mask(mask, ind_j, ind_k,
_MM_CMPINT_GE);
ind_jk = _mm512_mask_sub_epi32(ind_j, mask, ind_j, ind_k);
q = _mm512_mask_i32gather_ps(q, mask, ind_jk, m, _MM_SCALE_4);
mask = mask & _mm512_mask_cmp_ps_mask(mask, t, q,
_MM_CMPINT_LT);
_mm512_mask_i32scatter_ps(m, mask, ind_j, q, _MM_SCALE_4);
ind_j = _mm512_mask_sub_epi32(ind_j, mask, ind_j, ind_k);
}
while (mask != 0x0);
_mm512_i32scatter_ps(m, ind_j, t, _MM_SCALE_4);
}
Опишем полученный векторизованный вариант цикла. Название функции shell_sort_step_big_i16 означает, что функция выполняет 16 совмещенных итераций внутреннего цикла при выполнении прохода для некоторого большого k ≥ 16. Внутри функции используется глобальная переменная ind_straight, которая является целочисленным вектором, содержащим числа от 0 до 15. Данный вектор нужен для первоначального чтения из памяти 16 последовательных элементов массива с помощью операции i32gather (данное действие выполнено с помощью операции i32gather, так как в общем случае обращение не является выровненным). При выполнении всех векторных операций в теле цикла используется маска mask, которая инициализируется значением 0xFFFF (все 16 итераций выполняются). По мере исполнения кода маска прорежается, и цикл заканчивает свою работу, когда маска окончательно обнуляется. В конце работы функции происходит запись элементов вектора t на нужные места массива согласно значениям индексов ind_j.
Анализ эффективности
Для анализа достигнутого эффекта были выполнены замеры времени исполнения оригинального кода и модифицированной версии. Исходные коды собирались компилятором icc с использованием уровня оптимизации -O3, с включенной оптимизацией inline и с разрешением использования набора инструкций AVX-512. Так как описанный выше подход годится только для векторизации проходов для k ≥ 16 (для больших шагов), то отдельно выполнялись замеры времени работы проходов на больших шагах. Исполняемый код запускался на одном узле в одном процессе Intel Xeon Phi 7290 Knights Landing. Вычислительные узлы, базирующиеся на данных процессорах, входят в состав сегмента МВС-10П МП2 KNL, суперкомпьютера МВС-10П, находящегося в МСЦ РАН. Сортировка применялась к вещественным массивам, содержащим элементы типа float, инициализированные равномерно распределенными случайными значениями от 0.0 до 1.0. Размер массива изменялся от 10 тыс. до 2 млн. элементов. На рисунке 3 показаны результаты выполненных замеров. Видно, что максимальное ускорение проходов на больших шагах составляет чуть более 30 % и деградирует по мере увеличения длины массива в район 15 %. Суммарное ускорение всего вызова функции сортировки в пике составляет около 20 %, деградируя по мере увеличения длины массива до 10 %.
Полученные результаты требуют анализа, так как они расходятся с оптимистическим ожиданием кратного ускорения. В первую очередь обратим внимание на деградацию ускорения при увеличении размера массива. Эта деградация связана с использованием команд i32gather/i32scatter. Данные команды обладают большой латентностью и выполняются довольно долго, что делает их узким местом данного кода [30, 31]. Можно заметить, что команды i32gather/i32scatter, находящиеся в теле цикла, всегда обращаются к последовательным элементам массива. Несмотря на то, что данные блоки элементов не выровнены на 64 байта, заменим данные обращения командами load/score, так как накладные расходы, связанные с невыровненными обращениями, в данном случае более приемлемы, чем использование медленных инструкций i32gather/i32scatter. От финальной инструкции i32scatter избавиться не удастся, так как разброс ее индексов может быть произвольным. В итоге модифицированная версия кода будет выглядеть следующим образом:
void shell_sort_step_big_i16(float *m, int n, int k, int i)
{
int j = i;
__m512i ind_j = _mm512_add_epi32(ind_i, ind_straight);
__m512 t = _mm512_load_ps(&m[j]);
__mmask16 mask = 0xFFFF;
__m512 q;
do
{
mask = mask & _mm512_mask_cmp_epi32_mask(mask, ind_j, ind_k,
_MM_CMPINT_GE);
q = _mm512_mask_load_ps(q, mask, &m[j - k]);
mask = mask & _mm512_mask_cmp_ps_mask(mask, t, q,
_MM_CMPINT_LT);
_mm512_mask_store_ps(&m[j], mask, q);
ind_j = _mm512_mask_sub_epi32(ind_j, mask, ind_j, ind_k);
j -= k;
}
while (mask != 0x0);
_mm512_i32scatter_ps(m, ind_j, t, _MM_SCALE_4);
}
Для данной модификации кода также были выполнены аналогичные замеры времени исполнения и получены данные по ускорению для больших шагов проходов и для выполнения сортировки в целом. На рисунке 4, где представлены результаты этих замеров, видно, что векторизация для проходов с большими шагами приводит к ускорению в районе 70 % (в 3-4 раза), что дает более 50 % ускорения (более чем в 2 раза) для всей процедуры сортировки.
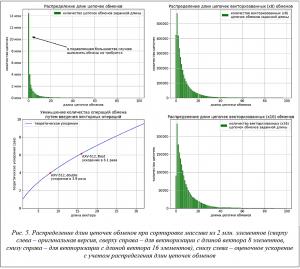
Однако проблемы с обращениями в память не являются основной причиной низкой эффективности применения векторизации. В качестве главного фактора выступает количество итераций внутреннего цикла реализации сортировки Шелла. Проведем исследование, на сколько позиций смещается элемент m[i] за время выполнения внутреннего цикла. Данную величину назовем длиной цепочки обменов, так как в процессе работы внутреннего цикла все элементы, начиная с m[i – 1] и заканчивая m[j] в конце цикла должны поменяться местами со своим соседом справа. Количество итераций внутреннего цикла может быть равно длине цепочки обменов, а может быть на единицу больше (зависит от условия выхода из цикла), так что, будем рассматривать только длины цепочек обменов. Рассмотрим первый проход при k0 = n /2. Во время данного прохода сортируются подмассивы, содержащие всего по два элемента, а значит, длина цепочки обменов может быть равна 0 или 1. На втором проходе при k1 = k0/2 длина цепочки обменов может изменяться уже от 0 до 3. По мере уменьшения шага прохода возможная длина цепочки обменов увеличивается обратно пропорционально уменьшению шага. На рисунке 5 сверху слева представлена диаграмма распределения длин цепочек обменов для проходов с большими шагами при сортировке массива из 2 млн. элементов. Из диаграммы видно, что в подавляющем большинстве случаев элементы стоят на своих местах и длина цепочки обменов равна нулю. Когда объединяем итерации промежуточного цикла с помощью широких команд, длина цепочки обменов будет представлять собой максимум из длин всех цепочек обменов объединенных оригинальных итераций.
На двух диаграммах на рисунке 5 справа можно видеть, к какому эффекту это приводит в случае объединения соседних итераций по 8 и 16 штук. Чтобы длина цепочки векторизованных обменов была нулевой, необходимо, чтобы нулевыми оказались все 8 (или соответственно 16) соседних цепочек обменов в оригинальной версии. Таким образом, резко возрастает количество ненулевых цепочек обмена.
В результате возрастания количества ненулевых цепочек обменов в векторизованной версии оценочное ускорение падает с 8 до 3,9 раза для длины вектора 8 и с 16 до 6,1 раза для длины вектора 16. На рисунке 5 снизу слева приведен график оценочного ускорения, связанного с уменьшением количества операций от длины вектора (отметим, что график существенным образом зависит от профиля исполнения программного кода и посчитан для конкретного кода выполнения проходов сортировки Шелла для больших шагов). То есть для векторизации вычислений с типом float сразу имеем трехкратные потери от теоретического ускорения, связанные просто с разбросом по количеству итераций внутреннего цикла на соседних итерациях промежуточного цикла. Данный фактор является крайне негативным.
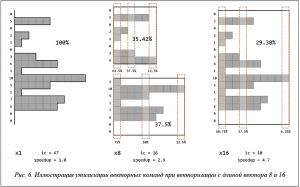
В качестве иллюстрации на рисунке 6 приведен пример распределения длин цепочек обменов с длиной вектора 16 соседних итераций промежуточного цикла. В случае невекторизованного кода имеем 47 скалярных обменов. При векторизации вычислений с длиной вектора 8 последовательность цепочек обменов разбивается на две цепочки векторизованных обменов, длина каждой из которых определяется по максимальной длине цепочки из соответствующей группы. Выполнение двух векторизованных цепочек обменов иллюстрируется двумя описанными прямоугольниками (рис. 6, в центре), общее количество обменов равно сумме длин этих прямоугольников. Белые области внутри прямоугольников означают, что соответствующие обмены будут замаскированы, таким образом, процент утилизации векторной команды падает. Для векторизации с длиной вектора 16 процент утилизации падает еще сильнее. Однако, несмотря на низкий процент утилизации векторных команд, он компенсируется уменьшением общего числа векторных инструкций в 8 и 16 раз соответственно.
Заключение
В статье рассмотрен подход к векторизации гнезда циклов со сложным управлением, содержащего внутренний цикл с неизвестным числом итераций. Для применения векторизации описано преобразование программного псевдокода в предикатную форму и избавление от лишних выходов из цикла. На производительность векторизованного кода отрицательно влияют негативные факторы.
Первым негативным фактором является то, что векторизация гнезда циклов с неизвестным числом итераций внутреннего цикла очень рискованна при отсутствии информации о профиле исполнения программы. Другими негативными факторами для проведения векторизации являются зависимость адресов обращения в память от количества итераций в таких циклах, а также чрезмерное использование медленных команд (например, i32gather/i32scatter).
Работа выполнена в МСЦ РАН в рамках государственного задания по теме 0065-2018-0409 «Разработка архитектур, системных решений и методов для создания вычислительных комплексов и распределенных сред мультипетафлопсного диапазона производительности, в том числе нетрадиционных архитектур микропроцессоров». При проведении исследований использовался суперкомпьютер МВС-10П, находящийся в МСЦ РАН.
Литература
1. Krappel T., Riedelbauch S. Scale resolving flow simulations of a Francis turbine using highly parallel CFD simulations. High Performance Computing in Science and Engineering'16. Springer Intern. Publ., 2016, pp. 499–510.
2. Fu H.H., Liao J.F., Yang J.Z., et al. The Sunway TaihuLight supercomputer: system and applications. Sci. China Inf. Sci., 2016, vol. 59, no. 7, pp. 072001. DOI: 10.1007/s11432-016-5588-7.
3. Klenk B., Fröning H. An overview of MPI characteristics of exascale proxy applications. Proc. ISC High Performance. J.M. Kunkel et al. (eds.), LNCS, 2017, vol. 10266, pp. 217–236.
4. Baranov A., Telegin P., Tikhomirov A. Comparison of auction methods for job scheduling with absolute priorities. Proc. Conf. Parallel Computing Technologies (PaCT 2017), Malyshkin V. (eds.), LNCS, 2017, vol. 10421, pp. 387–395.
5. Аладышев О.С., Киселёв Е.А., Савин Г.И., Телегин П.Н., Шабанов Б.М. Влияние характеристик внешней памяти суперкомпьютерных комплексов на выполнение параллельных программ // Системы и средства информатики. 2014. Т. 24. Вып. 4. С. 111–123.
6. Рыбаков А.А. Внутреннее представление и механизм межпроцессного обмена для блочно-структурированной сетки при выполнении расчетов на суперкомпьютере // Программные системы: теория и приложения. 2017. Т. 8. Вып. 1. С. 121–134.
7. Бендерский Л.А., Любимов Д.А., Рыбаков А.А. Анализ эффективности масштабирования при расчетах высокоскоростных турбулентных течений на суперкомпьютере RANS/ILES методом высокого разрешения // Тр. НИИСИ РАН. 2017. Т. 7. № 4. С. 32–40.
8. Дикарев Н.И., Шабанов Б.М., Шмелев А.С. Моделирование параллельной работы ядер векторного потокового процессора с общей памятью // Программные системы: теория и приложения. 2018. № 1 (36). С. 37–52.
9. Jeffers J., Reinders J., Sodani A. Intel Xeon Phi processor high performance programming. Knights Landing Edition. Morgan Kaufmann Publ., 2016, 632 p.
10. Intel 64 and IA-32 Architectures Software Developer's Manual. Combined volumes: 1, 2A, 2B, 2C, 2D, 3A, 3B, 3C, 3D and 4. Intel Corporation. 2017. URL: https://software.intel.com/en-us/download/intel-64-and-ia-32-architectures-sdm-combined-volumes-1-2a-2b-2c-2d-3a-3b-3c-3d-and-4 (дата обращения: 18.05.2018).
11. Intel C++ Compiler 16.0 User and Reference Guide. Intel Corporation. 2015. URL: https://software.intel.com/en-us/articles/intel-c-compiler-160-for-windows-release-notes-for-intel-parallel-studio-xe-2016 (дата обращения: 18.05.2018).
12. Intel Intrinsics Guide. URL: https://software.intel.com/sites/landingpage/IntrinsicsGuide (дата обращения: 18.05.2018).
13. Bramas B. Fast sorting algorithms using AVX-512 on Intel Knights Landing. arXiv: 1704.08579
[cs. MS]. URL: https://arxiv.org/abs/1704.08579 (дата обращения: 18.05.2018).
14. Krzikalla O., Wende F., Höhnerbach M. Dynamic SIMD Vector Lane Scheduling. In: ISC High Performance Workshops 2016, M. Taufer et al. (eds.), LNCS, 2016, vol. 9945, pp. 354–365.
15. Cook B., Maris P., Shao M. High Performance Optimizations for Nuclear Physics Code MFDn on KNL. In: ISC High Performance Workshops 2016, M. Taufer et al. (eds.), LNCS, 2016, vol. 9945, pp. 366–377.
16. Deslippe J., da Jornada F.H., Vigil-Fowler D. et al. Optimizing Excited-State Electronic-Structure Codes for Intel Knights Landing: A Case Study on the BerkeleyGW Software. In: ISC High Performance Workshops 2016, M. Taufer et al. (eds.), LNCS, 2016, vol. 9945, pp. 402–414.
17. Рыбаков А.А. Оптимизация задачи об определении конфликтов с опасными зонами движения летательных аппаратов для выполнения на Intel Xeon Phi // Программные продукты и системы. 2017. Т. 30. № 3. C. 524–528.
18. Maleki S., Gao Ya., Garzarám M.J., Wong T., Padua D.A. An evaluation of vectorizing compilers // Proc. Int. Conf. on Parallel Architectures and Compilation Techniques (PACT'11), 2011, pp. 372–382.
19. Extended test suite for vectorizing compilers. URL: http://polaris.cs.uiuc.edu/~maleki1/TSVC.tar.gz
(дата обращения: 18.05.2018).
20. Toro E.F. Riemann solvers and numerical methods for fluid dynamics. A practical introduction. Springer, 1999, 645 p.
21. Muchnick S. Advanced compiler design and implementation. SF, Morgan Kaufmann Publ., 1997, 856 p.
22. Allen R., Kennedy K. Optimizing compilers for modern architectures. SF, Morgan Kaufmann, 2002,
816 p.
23. Hutton G. A tutorial on the universality and expressiveness of fold. J. Functional Programming, 1999, vol. 9, no. 4, pp. 355–372.
24. Кнут Д. Искусство программирования. Т. 3: Сортировка и поиск. M.: Вильямс, 1994. 832 c.
25. A102549. Optimal (best known) sequence of increments for shell sort algorithm. URL: https://oeis.org/A102549 (дата обращения: 18.05.2018).
26. Ciura M. Best Increments for the Average Case of Shellsort. Proc. 13th Intern. Sympos. on Fundamentals of Computation Theory, LNCS, Riga, Latvia, 2001, vol. 2138, pp. 106–117.
27. Волконский В.Ю., Окунев С.К. Предикатное представление как основа оптимизации программы для архитектур с явно выраженной параллельностью // Информационные технологии. № 4. 2003.
C. 36–45.
28. Sloss A., Symes D., Wright C. ARM System developer's guide. Designing and optimizing system software, SF, Morgan Kaufmann, 2004, 690 p.
29. Ким А.К., Перекатов В.И., Ермаков С.Г. Микропроцессоры и вычислительные комплексы семейства «Эльбрус». СПб: Питер, 2013. 273 c.
30. Fog A. Instruction tables. List of instruction latencies, throughputs and micro-operation breakdowns for Intel, AMD and VIA CPUs. 2018. URL: http://www.agner.org/optimize/instruction_tables.pdf/ (дата обращения: 18.05.2018).
31. Intel 64 and IA-32 architectures optimization reference manual. Intel Corporation. 2016. URL: https://www.intel.com/content/dam/www/public/us/en/documents/manuals/64-ia-32-architectures-optimization-manual.pdf (дата обращения: 18.05.2018).



Comments