The peculiarities of the extra-large integrated circuits based on basic standard library elements are in use of pre-designed library elements and macroblocks. The macro-arrangement of the semi-custom VLSI topology determines the placement of blocks and tracing of interconnects. The placement purpose is in finding a specific position on the topology for each element.

The problem of placing VLSI elements [1-3] belongs to the class of NP-complicated combinatorial optimization problems. It is rather well studied, and there are plenty of algorithms allowing to solve it. Currently, the methods based on the artificial intelligence [4, 5] are applied more and more often. Such methods rely on the collective intelligence modelling [6-8] and also include the bee colony method [9-12].

The communities of these insects possess a collective intelligence. The behavior organization provides these communities with a possibility to do the tasks that cannot be completed by each insect in particular. This is achieved through collective action and a simple cooperation among community members. Such communities have self-organization and adaptation skills.

The algorithms based on such communities’ skills lie in the movement of the community members (agents). The agents move by positions. The value of the target function depends on the positions determined by agents. The plenty of particles and bees are presented as a multi-agent system, where each particle or bee is moving independently according to trivial rules.

Having analyzed the known approaches for solving complicated tasks, it can be concluded that the use of some algorithm doesn’t give any guarantee of getting a quality solution. In this regard, currently one of the ways to enhance the effectiveness of the methods of finding a global optimum for solved problems is in the hybridization of algorithms [13]. A special feature of a hybrid algorithm is the fact that the advantages of one algorithm can compensate for the disadvantages of the other. The combination of various search algorithm methods provides the possibility to determine a bigger area of acceptable solutions and to find a more optimal solution.

The work describes the developed algorithm for solving the problem of placing the VLSI elements combining the behavior procedures of a bee community and a particle swarm.

Problem statement and concept of placing the elements by the sequence pair method

The characteristics that determine the essence of a placement problem statement are the model of presenting the placed (construction) elements as geometric objects; the model of the installation space (space of positions), the model of presenting an electric principle diagram, the character of the target function for the placement evaluation [3, 14]. It is necessary to place the elements on the commutation field with an optimization of some quality criteria.

The main known placement criteria [1, 3, 14] are the total connection length, the length of the longest connection, the number of possible intersections, the number of the connection bends, the chip area etc.

Let’s consider the concept of placing the elements by the sequence pair method [15]. The pair of sequences A₁ and A ₂  is a pair of ordered lists of the same set of elements. |A ₁|=|A₂|=n. Let there be a pair of sequences (A₁ = 4, 3, 1, 6, 2, 5; A ₂ = 6, 3, 5, 4, 1, 2). A constraint graph for the given pair of lists is formed through a sequential building of a meta net with 45 degrees tip (fig. 1).

For each element, the plain is divided into four sectors by two inclined lines. The sequential pair defines the relation for some pair of elements a_i and a_j, contained from these lists,
in the following way:

If (A₁ = <…, a_i, …, a_j, …>, A₂ = <…,a_i, …, a_j, …>), thena_j is to the right of a_i;

If (A₁ = <…, a_i, …, a_j,… >, A₂ = <…, a_j, …, a_i, … >), then a_j is lower than a_i .

Let us consider the location of elements in relation to element 1.

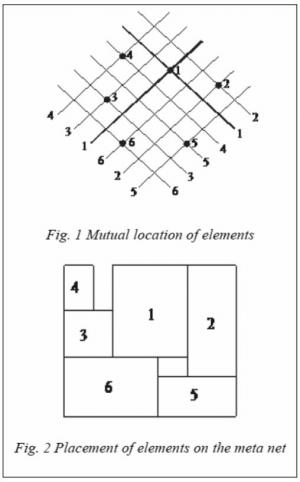For this pair of sequences element 2 is located in the right sector from element 1 (fig. 2), as in both sequences element 2 is to the right of 1. Elements 6 and 5 are in the lower sector from element 1 etc.

Therefore, having a pair of sequences ((A₁, A ₂) defining the horizontal relation between the elements, we can build a horizontal constraint graph R_h(V_h , E_h) as follows:

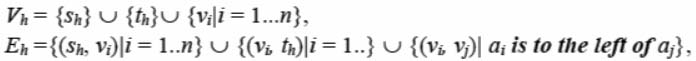
where v_i corresponds to an element,s_h is an initial node (left border)), t_h is a final node (right border). The weight of the node v_i is equal to the width of the elementa_i. The weight of nodes s_h, t_h is zero.

The vertical constraint graph R_v(V_v , E_v) is built in the similar way.

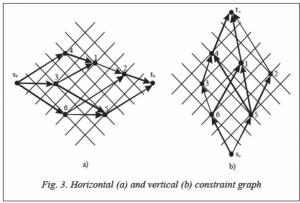Example: on figure 3 there are both graphs for the placement presented on figure 2.

Both graphs have weighted nodes, are directed and acyclic, i.e. we can use the algorithm of finding the longest way to determine coordinates XY for each element.

As an element’s coordinate, we will consider the coordinate of its lower left corner.

The use of the sequence pair method allows moving from a pair of sequences to the placement in two stages. First, the move to the constraint graph or to the ordered tree (OT) covering the constraint graph is made, then, using a trivial algorithm, the plan or placement
of elements is built over the constraint tree.

Approach to the presentation of solutions in the algorithm based on the swarm intelligence

In the particle swarm optimization method, the agents are particles in the parameter space of the optimization task. Each particle is connected with the entire swarm, can cooperate with the entire swarm and is attracted towards the best swarm’s decision. At any moment of time (at each iteration) the particles take some positions in this space. For each position of a particle, the corresponding target function value is calculated. While determining the upcoming position of a particle, the information about the best particle among the neighbors of this particle, as well as the information about this particle at that iteration is taken into account, when the best target function value corresponded to this particle; on this basis, a particle changes its position in the search space according to certain rules [7, 8].

The main idea of the bee community paradigm [8-13] lies in the performance of the two-level search strategy. First, some number of scout bees that search for places with nectar fly out of the hive in a random direction. After a while, the bees come back to the hive and report to others in a special way, where and how much nectar they’ve found. After that, other bees go to the found places. Moreover, the more nectar is supposed to be found on a spot, the more bees fly in this direction. The scouts go to search for other spots, and after that the process is repeated. The goal of a bee community is to find a place where the maximum amount of nectar is located.

Unlike the canonical particle swarm paradigm, the hybrid algorithms as models for presenting the solutions, use a wide range of graph structures (a route, a tree, a bigraph, a matching, an internally stable set etc.) [14-22], where the solutions may be presented as various graph structures.

This doesn’t allow using the canonical particle swarm paradigm directly (for example, a problem of a directed mutation of one tree towards another is quite nontrivial from a formal point of view).

Due to this, a development of a modernized search space structure, a data structure for presenting solutions and positions, modernized mechanisms of particle movements in the search space are urgent.

There is an offered approach to building a modified particle swarm paradigm, which enables simultaneous use of chromosomes with integer parameter values in the bees algorithm and the algorithm based on a particle swarm.

Affine search space

Let there be a linear vector space (LVS) with n-dimensional points as the elements. We compare any two points p and q of this space with the unique ordered pair of these points, which we’ll call a geometric vector (vector) further. p, q ∈ V( p, q) is a geometric vector (an ordered pair).

The set of all LVS points refilled by geometric vectors is called point-vector or affine space. The affine space is n- dimensional if the corresponding LVS is n-dimensional, too.

The affine relaxation particle swarm model (ARM) is a graph with the nodes matching the positions of a particle swarm, while the arcs match the affine connections between positions (points) in the affine space. The affinity is a proximity measure of two agents (particles). At every iteration, each agent p_i goes to a new state (position) in the affine space, so that the weight of an affine connection between the agent p_i and basic (best) agent p_* is being reduced. The movement of agent p_i to the new position x_i(t+1) from x_i( t) happens with the help of the relaxation procedure.

The special relaxation movement procedure depends on the data structure (chromosome) type: a vector, a matrix, a tree and their sets that is an interpretation of solutions.

The best particles from the point of the target function are declared “the center of attraction”. The displacement vectors of all particles in the affine space strive to these centers.

The movement is possible considering the proximity degree to one basic element or to a group of neighboring elements and considering the probability of movement to a new state.

Search by the particle swarm method

In the heuristic algorithms of the swarm intelligence, a swarm of particles inhabits the multidimensional search space [7, 8]. During the search process by the particle swarm method, each particle goes to a new position. A new position in the canonical particle swarm paradigm is determined in accordance with the methodology described in this paper [9].

Have a look at the mechanisms of a particle swarm in accordance with the concept of placing elements by the sequence pair method.

Suppose we have a particle swarm P = {p_k|k = 1, 2, …, n_k}. Each particle p_k on a step t is located in the position X_k(t). Since the placement is defined by a pair of ordered lists A₁ and A₂, position X_k(t) corresponding particle p_k, is determined by a set of 2 chromosomes corresponding to a pair of ordered lists A₁ and A₂ X_k (t) = {Н_k1(t), Н_k2(t)}.

Chromosome Н_ki(t) = { g_kil|l = 1, 2, …, n_l} is a set of n genes g_kil. A value of gene g_kil is equal to the value of a matching element from list A_i.

The search space of one chromosome includes the number of axes X_il equal to the number of genes in the chromosome Н_ki(t). In the chromosome Н_ki(t) an axis (axis number) fits to each gene. The base points on each axis X_il are integers in the range from 0 to n.

Suppose the list B = <1, 7, 21, 4, 8, 18> be used as a basic list. |B| = 6. Search space X includes 6 axes: X ₁-X₆, in accordance with the number of list elements. Each axis fits to a list position. The reference points x_ij on the axis X_i = <x_ij|j=1, 2, …, 6> are ordered values of list B:

X_i = <x_i1 = 1, x_i2 = 7, x_i3 = 21, x_i4 = 4, x_{i 5} = 8, x_i6 = 18> = <1, 7, 21, 4, 8, 18>.

For example: List M_i = <21, 8, 7, 1, 8, 4, 18> is presented as position Н_i = {x₁₃, x₂₅, x₃₂,x₄₁, x₅₄, x₆₆} .

Have a look at the movement procedure that happens with the help of the directed mutation operation (DMO), which the authors have developed. It lies in the change of the mutual location of elements in the list. Particle p_i is moving from the position Н_i(t) towards to new position Н_i(t + 1) with a new mutual location of elements in the list. The paper describes the process of the directed mutation operation in details [9].

Example of the movement procedure process (DMO).

Let positions Н_i(t) и H_z(t) be as follows:

H_z (t) = {1, 10, 2, 3, 8_,}, H_i( t) = {1, 3, 2, 10, 8_,}.

On the first cycle, the set of pairs D₁=(1, 3), (2, 10) is formed. The mutual locations of pair elements (1, 3) in Н_i(t) and H_z(t) coincide while the ones of pair (2, 10) don’t. Therefore S_iz(t) = 1. In H_i(t) the elements of pair
(2, 10) are interchanged. H_i(t + 1) = {1, 3, 10, 2, 8}.

On the second cycle, the set of pairs D₂=(3, 10), (2, 8) is formed. The mutual locations of pair elements (10, 8) in Н_i(t + 1) and H_z(t) coincide while the ones of pair (2, 10) don’t. Hence S_iz(t )=1. In H_i(t + 1) the elements of pair (3, 2) are interchanged. H_i(t + 2) = {1, 3, 10, 2, 8}.

The main purpose of the movement of the particle p_k is to find a place with the best mark by it. The common purpose of a particle swarm is to receive an optimal placement solution.

Adaptive behavior of a bee colony.

Suppose we have a bee community P = {p_k|k =1, 2, …, n_k}. At the first iteration (t = 1) the scout bees are randomly placed in the solution search area. Each scout beep_k on step t chooses position X_k(t). Each position is an analog of a nectar spot and a model of a placement problem solution. The nectar volume is a criterion value at this point.

Like in the particle swarm algorithm, position Xk(t) selected by a bee is defined by a set of 2 chromosomes corresponding to a pair of ordered lists A1 and A2. Xk(t) = {Нk1(t), Нk2(t)}.

Chromosome Н_ki(t) = { g_kil|l = 1, 2, …, n_l} is an ordered set of n genes g_kil. The value of gene g_kil is equal to a value of a corresponding element in list A_i.

The first operation that a bee swarm carries out lies in the random generation of a set of (positions) solutions X(t) = {X_k(t)|k = 1, 2, …,n_r} that differ from one another. For each solutionX_k(t) a value of target function F_k is calculated. In set X(t) n _б of the best solutions are selected, which belong to the set of basic solutions (positions) X^b(t). At the second approach, the probabilistic choiceX^b (t) takes place. Probability p(X^b_k) of choosing basic position X^b_k Î X^b ( t) by a foraging agent is proportional to the value of target function F^b_k in this position and is defined as follows:

p (X^b_k(t)) =F^b_k(t) / ∑_k(F^b_k(t)) .

At each iteration, a movement from one population of basic positions to another takes place.

The formation of new solution X^b_k(t+1) lying in θ – neighborhood of basic position X^b_k(t) happens in the way δ of selective (random) pair interchanges of neighbored elements in vectorX^b_k(t). We will take that solution X^b_k (t + 1) lies in θ – neighborhood of solution X^b_k(t), if X^b_k(t + 1) was received in the way θ of random pair interchanges of neighbored elements in list X^b_k(t).

For each basic position X^b_k(t) Î X^b(t), the probabilistic choice of a set of positions O^b_k(t + 1) takes place, which are located in θ – neighborhood of basic position X^b_k(t).

Let us call the set of positions chosen in θ – neighborhood of positionX^b_k(t) as O^b_k(t + 1). The evaluation of each position of set O^b_k(t + 1) is calculated. In each θ – neighborhood O^b_k(t + 1) the best position is selected. The best positions of θ – neighborhoods form an new set of basic positions X^b(t + 1).

The best solution (position) of set X^b (t + 1) is saved, and then there’s a movement to the next iteration. At the beginning of the second and at the subsequent iterations, first of all, a set of basic positions X^b (t) (t = 2, 3, …, L) is formed, which is created of two parts X^b1(t) and X^b2(t), X^b1(t) È X^b2(t) =X^b(t). In the first partX^b1(t) n^b₁ of the best position are being included among positions X^*_k(t – 1) that agents have found in each area formed at the previous iteration. The agents form the second part X^b2(t) in the same way as at the first iteration. Next, the actions similar to the actions considered at the first iteration takes place.

Hybridization of the swarm intelligence structure.

The algorithms based on a collective behavior contain a solution search area, there is a swarm of agents. The location of each agent is some solution. Finding a solution is the movement of agents in the acceptance region. On our case, a swarm is as a plenty of solutions and a bee (particle) is as an agent, which allows forming hybrid solution search procedures by uniting the models of a particle swarm and a bee community on the collective adaptation basis.

The developed algorithm for solving the placement problem of the VLSI elements uses the bionic search architecture and consists of united procedures of a bee community and a particle swarm. It helps to get out of local holes and increases the algorithm convergence. The data is in a matrix or vector form.

Each particle p_k on step t is in position X_k(t), as the placement is defined by a pair of ordered lists A₁ and A₂ . Position X_k(t) corresponds to particle p_k, and it is defined by a set of 2 chromosomes corresponding to the pair of ordered lists A₁ and A₂ X_k(t) = {Н_k1(t), Н_{k 2}(t)}.

Chromosome Н_ki(t) = { g_kil|l = 1, 2, …, n_l} is a plenty of n genes g_kil. The value of gene g_kil is equal to the value of a corresponding element in list A_i.

During the movement in the acceptance region, the community of agents is as a bee community by turn or a particle community with certain characteristic of the adaptive behavior.

The hybridization is next. First, a swarm of locations X(t) = {X_k(t)|k =1, 2, …, n_r} forms with the help
of the particle swarm algorithm. Using the particle swarm methodology, there are the particle swarm places X(t) in the virtual value space, at displacement the particles from place X( t – 1). According to the proposed approach to the integration, new positions are as basic positions X ^b(t) those a swarm of scout bees have discoved. Next, in accordance with the bee colony mechanisms, forager bees inspect θ – neighborhoods of each basic position of set X^b (t). The key operation of the bees algorithm is the research of promising positions and their θ – neighborhoods in the solution space. In each θ – neighborhood O^b_k( t + 1) they choose the best position. The best position of θ – neighborhoods create a new set of basic positions X ^b(t + 1). At the subsequent iteration (t+1), the set of positions X^b( t + 1) is considered as a set of positions of a particle swarm. The total estimation of the dependence of the hybrid algorithm’s working time is in the range О(n²) – О( n³).

Experimental research

The research of a swarm placement algorithm (SPA) consists of the forming test problems for a placement problem with a present optimal result (PEKO) [22]. The both formats GSRC Book Shelf and LEF/DEF have the optimal results of PEKO and they are in the Net [23, 24].

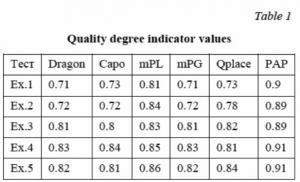
All the circuits in REKO are local, i.e. the length of the conductors in each circuit has the lowest possible value. The PEKU setting schemes consist of local circuits in PEKO style. For the experimental researches of the developed placement program they used the PEKU setting schemes with a known optimum F_op: Ex. 1 per 30 blocks, Ex.2 – 60, Ех.3 – 90, Ех.4 – 120, Ех.5 – 150. For comparison, the authors chose the modern placement algorithms: Dragon v2.20 [25], Capo v.8. [26], mPL v.2.0 [27], mPG v1.0 [28] и QPlace v.5.1. [29].

To determine the optimality of the achieved values, the authors calculated the parameter: the length of a connection to the best length of the connections (for PEKO) or (for G-PEKU and PEKU). This ratio is a degree of quality. No one of the placement algorithm achieved the quality ratio value close to 1 during the research.

Table 1 shows the received values of the quality degree indicator for a range of known algorithms and SPA algorithm.

The quality degree of the developed SPA program is 10% higher than of the programs Dragon, Capo, mPL, mPG и Qplace. ВСА О(n²).

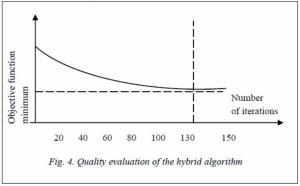
The authors put into practice еhe algorithm convergence analysis of SPA in a certain way. They ran each test task for completion for 10 times. For each test, they defined an iteration number, after which no criterion improvement happened next. Fig. 4 shows the experiment results. The test revealed that the algorithm determines the best result at iteration 111-131. The algorithm converged at iteration 128 (fig. 4).

The time complexity of the algorithm with the fixed values of the population size and number of generations is О(n). The total time complexity of the hybrid algorithm is О(n ²) – О(n³).

Conclusion.

The analysis of the known methodologies applied for receiving optimal solutions in the combinatorial logical tasks has determined the choice of approaches containing the collective behavior models. These approaches allow solving difficult problems, which achieve the optimal criterion values in acceptable time.

The algorithm consists of combined procedures of a bee community and a particle swarm, which allows getting out of “local holes” and increases the algorithm convergence. In the suggested method the authors shows the data in the matrix or vector form.

The paper describes a modified particle swarm paradigm ensuring, unlike the canonical method, the possibility to search for solutions in the affine space with integer parameter values. The authors have considered the mechanisms of the particles’ movement in the affine space for reducing the weight of affine connection. They describe directed mutation operators, the essence of which lies in the change of integer gene values in a chromosome. They suggested a modified bees algorithm structure. For each basic position, they carried out a probabilistic choice of a set of positions located in the neighborhood of a basic positions.

The improvement of the work quality of the developed algorithm is possible by setting up the control parameter values.

The time complexity of the algorithm with the fixed values of a population size and number of generations is О(n). In total, the dependence of the working time of the hybrid algorithm is О( n²) – О(n³).

Acknowledgements: This work was supported by the RFBR, grant no. 18-07-00737 А.

References

1. Norenkov I.P. The Basics of the Computer-Assisted Design. Moscow, BMSTU Publ., 2006, 248 p.

2. Alpert C.J., Mehta D.P., and Sapatnekar S.S. (eds.). Handbook of Algorithms for Physical Design Automation. Boston, MA, Auerbach Publ., 2009, 1042 p.

3. Kazennov G. The basics of the design of integrated circuits and systems. Moscow, 2005, 435 p.

4. Wang X. Hybrid nature-inspired computation method for optimization. PHD Thes. Helsinki Univ. of Technology, 2009, 161 p.

5. Karpenko A.P. The modern search optimization algorithms. Algorithms inspired by the nature . Moscow, BMSTU Publ., 2014, 448 p.

6. Poli R. Analysis of the publications on the applications of particle swarm optimisation. Journal of Artificial Evolution and Applications, 2008, Art. ID 685175. DOI: 10.1155/2008/685175.

7. Clerc M. Particle Swarm Optimization. ISTE Publ., London, UK, 2006, 198 р.

8. Kennedy J., Eberhart R.C. Particle swarm optimization. Proc. IEEE ICNN’95, Perth, Australia, 1995, pp. 1942–1948.

9. Lebedev B.K., Lebedev O.B., Lebedeva E.O., Nagabedyan A.A. The hybrid global optimization swarm algorithm in the affine search space. Programmnye Produkty, Sistemy i Algoritmy, 2019, no. 1. Available at: http://swsys-web.ru/en/hybrid-swarm-algorithm-global-optimization.html (acсessed October, 20, 2019). DOI: 10.15827/2311-6749.30.348.

10. Lučić P., Teodorović D. Computing with bees: Attacking complex transportation engineering problems. Int. J. Artif. Intell. Tools, 2003, no. 12, pp. 375–394.

11. Quijano N., Passino K.M. Honey Bee Social Foraging Algorithms for Resource Allocation: Theory and Application . Columbus, Ohio State Univ. Publ., 2007, 39 p.

12. Lebedev V.B. The bee colony method in combinatorial problems on graphs.Proc. 13^th Russian Conf. on Artificial Intelligence RCAI-2012, Belgorod, 2012, vol. 2, pp. 414-422.

13. Lebedev B.K., Lebedev V.B. Placement on the basis of the bee colony method. Bull. YuFU, 2010, no. 12, pp. 12-18.

14. Lebedev B.K., Lebedev V.B., Lebedev O.B. Methods, Models and Algorithms of Placement. Rostov on Don, YuFU Publ., 2015, 181 p.

15. Хu J., Guo P.-N., Cheng C.-K. Sequence-pair approach for rectiliner module placement. IEEE Trans. Computer-Aided Design of Integrated Circuits and Systems , 1999, vol. 18, no. 4, pp. 484-493.

16. Lebedev B.K., Lebedev V.B. Coverage by the particle swarm method. Proc. VI Int. Conf. Integrated Models and Soft Computations in the Artificial Intelligence , Kolomna, 2011, pp. 611-619.

17. Lebedev B.K., Lebedev О.B., Lebedeva Е.М. Distribution of resources based on hybrid models of swarm intelligence. Sci. and Tech. J. of Information Technologies, Mechanics and Optics. 2017. vol. 17, no. 6, pp. 1063–1073. DOI: 10.17586/2226-1494-2017-17-6-1063-1073.

18. Lebedev B.K., Lebedev V.B. Tracking on the basis of the particle swarm method. Proc. 12^th Russian Conf. on Artificial Intelligence RCAI-2010, Tver, 2010, vol. 2, pp. 414-422.

19. Lebedev B.K., Lebedev О.B., Lebedev V.B. Swarm intelligence hybridization in the genetic evolution in terms of placement. Programmnye Produkty, Sistemy i Algoritmy, 2017, no. 4. Available at: http://swsys-web.ru/en/hybridization-of-swarm-intelligence-and-genetic-evolution.html (acсessed October 20, 2019). DOI: 10.15827/2311-6749.25.280.

20. Lebedev B.K., Lebedev V.B. Planning on the basis of the swarm intelligence and genetic evolution. Bull. YuFU, 2009, no. 2, pp. 25-33.

21. Lebedev B.K., Lebedev О.B. Lebedeva Е.О. Swarm algorithm for scheduling of multiprocessor systems. Engineering Journal of Don, 2017, no. 3. Available at: http://www.ivdon.ru/uploads/article/pdf/
IVD_111_lebedev_lebedev.pdf_411ed63380.pdf (acсessed October 20, 2019).

22. Cong J., Romesis M., Xie M. Optimality, Scalability and Stability Study of Partitioning and Placement Algorithms. Proc. of the Int. Sympos. on Physical Design, Monterey, CA, 2003, pp. 88-94.

23. Cong J., Romesis M., Xie M. UCLA Optimality Study Project. 2004. Available at: http://cadlab.cs.ucla.edu/~pubbench (acсessed October 20, 2019).

24. MCNC. Electronic and Information Technologies. Available at: www.mcnc.org (acсessed October 20, 2019).

25. Wang M., Yang X. and Sarrafzadeh M. Dragon2000: Standard-cell placement tool for large industry circuits. Proc. IEEE/ACM ICCAD, 2000, pp. 260-263.

26. Caldwell A.E., Kahng A.B. and Markov I.L. Can recursive bisection alone produce routable placements. Proc. DAC, 2000, pp. 477-482.

27. Chan T., Cong J., Kong T., Shinnerl J., Sze K. An enhanced multilevel algorithm for circuit placement. Proc. IEEE ICCAD, San Jose, CA, 2003, pp. 299-306. DOI: 10.1109/ICCAD.2003.30.

28. Yang X., Choi B.-K. and Sarrafzadeh M. Routability-driven white space allocation for fixed-die standard-cell placement. Proc. IEEE Trans. on Computer-Aided Design of Integrated Circuits and Systems , 2003, vol. 22, issue 4, pp. 410-419. DOI: 10.1109/TCAD.2003.809660.

29. CDNS. Envisia Ultra Placer Reference. QPlace version 5.1.55. Available at: http://www.cadence.com (acсessed October 20, 2019).

УДК 621.3.049.771

DOI: 10.15827/2311-6749.19.4.1

РЕШЕНИЕ ЗАДАЧИ РАЗМЕЩЕНИЯ ЭЛЕМЕНТОВ СБИС НА ОСНОВЕ ИНТЕГРАЦИИ МОДЕЛЕЙ РОЕВОГО ИНТЕЛЛЕКТА В АФФИННЫХ ПРОСТРАНСТВАХ ПОИСКА

Б.К. Лебедев ¹ , д.т.н., профессор, lebedev.b.k@gmail.com

О.Б. Лебедев ¹ , к.т.н., доцент, lebedev.ob@mail.ru

Е.О. Лебедева ¹ , аспирант, lbedevakate@mail.ru

А.А. Нагабедян ¹ , магистрант, andrewnagabedyan@yandex.ru

¹ Институт компьютерных технологий и информационной безопасности Южного федерального университета, кафедра систем автоматизированного проектирования, 347928, Россия, г. Таганрог )

В работе описана архитектура многоагентной системы на основе природных вычислений. Система выполняет размещение компонентов сверхбольших интегральных схем, используя объединенные модели роевого интеллекта. Предложены новые структуры представления решения задачи размещения элементов сверхбольших интегральных схем в виде хромосом. Представлена модифицированная парадигма роя частиц, отличающаяся от канонической, возможностью использования в аффинном пространстве позиций с целочисленными значениями параметров.

Передвижение роя частиц в рассматриваемой области решений достигается при помощи разработанного оператора, называемого направленная мутация. Предложена модифицированная структура алгоритма пчел. Ключевой операцией алгоритма является исследование перспективных позиций, лежащих в окрестностях базовых позиций.

Тестовые испытания доказали, что при интеграции моделей поведения роя пчел и роя частиц, результаты нового гибридного алгоритма получаются на 11 – 18 % лучше, чем у каждого алгоритма по отдельности.

Ключевые слова: СБИС, размещение, роевой интеллект, пчелиный алгоритм, рой частиц, гибридизация. многоагентная система, аффинное пространство поиска, оператор направленной мутации, окрестность базовых позиций, бионический поиск.

Благодарности: работа выполнена при финансовой поддержке гранта РФФИ, проект № 18-07-00737 А.

Литература

1. Норенков И.П. Основы автоматизированного проектирования. М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. 248 с.

2. Alpert C.J., Mehta D.P., and Sapatnekar S.S. (eds.). Handbook of Algorithms for Physical Design Automation. Boston, MA, Auerbach Publ., 2009, 1042 p.

3. Казеннов Г. Основы проектирования интегральных схем и систем. М.: Бином. Лаборатория знаний, 2005. 435 с.

4. Wang X. Hybrid nature-inspired computation method for optimization. PHD Thes. Helsinki Univ.
of Technology, 2009, 161 p.

5. Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой. М.: Изд-во МГТУ им. Н.Э. Баумана, 2014. 448 с.

6. Poli R. Analysis of the publications on the applications of particle swarm optimisation. Journal of Artificial Evolution and Applications, 2008, Art. ID 685175. DOI: 10.1155/2008/685175.

7. Clerc M. Particle Swarm Optimization. ISTE Publ., London, UK, 2006, 198 р.

8. Kennedy J., Eberhart R.C. Particle swarm optimization. Proc. IEEE ICNN’95, Perth, Australia, 1995, pp. 1942–1948.

9. Лебедев Б.К., Лебедев О.Б., Лебедева Е.О., Нагабедян А.А. Гибридный роевой алгоритм глобальной оптимизации в аффинном пространстве поиска // Программные продукты, системы и алгоритмы. 2019. № 1. URL: http://swsys-web.ru/en/hybrid-swarm-algorithm-global-optimization.html (дата обращения 20.10. 2019). DOI: 10.15827/2311-6749.30.348.

10. Lučić P., Teodorović D. Computing with bees: Attacking complex transportation engineering problems. Int. J. Artif. Intell. Tools, 2003, no. 12, pp. 375–394.

11. Quijano N., Passino K.M. Honey Bee Social Foraging Algorithms for Resource Allocation: Theory and Application. Columbus, Ohio State Univ. Publ., 2007, 39 p.

12. Лебедев В.Б. Метод пчелиной колонии в комбинаторных задачах на графах // XIII конф. по искусствен. интеллекту (КИИ-2012): сб. тр. Белгород, 2012. Т. 2. С. 414–422.

13. Лебедев Б.К., Лебедев В.Б. Размещение на основе метода пчелиной колонии // Изв. ЮФУ. 2010. № 12. С. 12–18.

14. Лебедев Б.К., Лебедев В.Б., Лебедев О.Б. Методы, модели и алгоритмы размещения. Ростов н/Д: Изд-во ЮФУ, 2015. 181 с.

15. Хu J., Guo P.-N., Cheng C.-K. Sequence-pair approach for rectiliner module placement. IEEE Trans. Computer-Aided Design of Integrated Circuits and Systems, 1999, vol. 18, no. 4, pp. 484–493.

16. Лебедев Б.К., Лебедев В.Б. Покрытие методом роя частиц // Интегрированные модели и мягкие вычисления в искусственном интеллекте: матер. VI Междунар. науч.-практич. конф. Коломна, 2011. С. 611–619.

17. Лебедев Б.К., Лебедев О.Б., Лебедева Е.М. Распределение ресурсов на основе гибридных моделей роевого интеллекта // Науч.-технич. вестн. ИТМО. 2017. Т. 17. № 6. С. 1063–1073. DOI: 10.17586/2226-1494-2017-17-6-1063-1073.

18. Лебедев Б.К., Лебедев В.Б. Трассировка на основе метода роя частиц. // XII конф. по искусствен. интеллекту (КИИ-2010): сб. тр. Тверь, 2010. Т.2. С. 414–422.

19. Лебедев Б.К., Лебедев О.Б., Лебедев В.Б. Гибридизация роевого интеллекта и генетической эволюции на примере размещения // Программные продукты, системы и алгоритмы. 2017. № 4. URL: http://swsys-web.ru/en/hybridization-of-swarm-intelligence-and-genetic-evolution.html (дата обращения 20.10.2019). DOI: 10.15827/2311-6749.25.280.

20. Лебедев Б.К., Лебедев В.Б. Планирование на основе роевого интеллекта и генетической эволюции // Изв. ЮФУ. 2009. № 2. С. 25–33.

21. Лебедев Б.К., Лебедев О.Б. Лебедева Е.О. Роевой алгоритм планирования работы многопроцессорных вычислительных систем // Инженерн. вестн. Дона. 2017. № 3. URL: http://www.ivdon.ru/uploads/article/pdf/IVD_111_lebedev_lebedev.pdf_411ed63380.pdf (дата обращения 20.10.2019).

22. Cong J., Romesis M., Xie M. Optimality, scalability and stability study of partitioning and placement algorithms. Proc. of the Int. Sympos. on Physical Design, Monterey, CA, 2003, pp. 88–94.

23. Cong J., Romesis M., Xie M. UCLA Optimality Study Project. 2004. URL: http://cadlab.cs.ucla.edu/
~pubbench (дата обращения 20.10.2019).

24. MCNC. Electronic and Information Technologies. URL: www.mcnc.org (дата обращения 20.10.2019).

25. Wang M., Yang X. and Sarrafzadeh M. Dragon2000: Standard-cell placement tool for large industry circuits. Proc. IEEE/ACM ICCAD, 2000, pp. 260–263.

26. Caldwell A.E., Kahng A.B. and Markov I.L. Can recursive bisection alone produce routable placements. Proc. DAC, 2000, pp. 477–482.

27. Chan T., Cong J., Kong T., Shinnerl J., Sze K. An enhanced multilevel algorithm for circuit placement. Proc. IEEE ICCAD, San Jose, CA, 2003, pp. 299–306. DOI: 10.1109/ICCAD.2003.30.

28. Yang X., Choi B.-K. and Sarrafzadeh M. Routability-driven white space allocation for fixed-die standard-cell placement. Proc. IEEE Trans. on Computer-Aided Design of Integrated Circuits and Systems, 2003, vol. 22, issue 4, pp. 410–419. DOI: 10.1109/TCAD.2003.809660.

29. CDNS. Envisia Ultra Placer Reference. QPlace version 5.1.55. Available at: http://www.cadence.com (acсessed October 20, 2019).