Нечеткие бинарные отношения представляют собой важное математическое понятие, позволяющее формулировать и анализировать математические модели реальных задач принятия решений, к которым относится и задача управления технологической безопасностью промышленных процессов. Отношение на множестве альтернатив в задачах такого типа выявляется обычно путем консультаций с экспертами, которые зачастую не имеют вполне четкого суждения об этом отношении. В подобных случаях нечеткое отношение служит удобной и более адекватной реальности формой представления исходной информации, чем обычное отношение.
Нечеткость позволяет экспертам (операторам, технологам), с помощью которых выявляется данное отношение на множестве возможных состояний технологического процесса (ТП), описывать степень своей убежденности в предпочтениях числами из интервала [0,1].
Нечеткие бинарные отношения
В данном разделе приводятся краткие сведения о нечетких бинарных отношениях [1–3] как чисто математическом объекте. Описываемые здесь свойства и особенности нечетких отношений будут использоваться в дальнейшем при поиске центра безопасности и построении модели развития опасностей.
Определение и операции с нечеткими множествами. Нечеткое множество А на элементах О определяется заданием отображения mА(х) элементов хÎО в интервал [0,1]. При этом mА(х) называется функцией принадлежности нечеткому множеству А элемента х, характеризующего степень истинности события {хÎА}, а множество А записывается в виде А={х, mА(х)}хÎО.
Функция принадлежности mА(х) является обобщением определения характеристической функции множества, принимающей лишь значения 0 или 1, при помощи которой может быть определено само множество в классической теории множеств.
Приведем следующие основные операции с нечеткими множествами:
– эквивалентность А¥В Û mА(х) = mВ(х);
– включение АÍВ Û mА(х) £ mВ(х);
– объединение АÈВ Û mА ÈВ(х) = mах{mА(х),mВ(х)};
– пересечение АÇВ Û mА ÇВ(х) = min{mА(х),mВ(х)};
– произведение А·В Û mА·В(х) = mА(х)mВ(х);
– сумма А+В Û mА+В(х) = mА(х)+ mВ(х) - mА(х)mВ(х);
– умножение А на aÎ[0,1]:a Û maА(х) = a mА(х);
– возведение А в степень a>0:Аa Û mАa(х) = (mА(х))a;
– концентрирование CON(A) = A2;
– растяжение DIL(A) = A0.5.
Нечеткое множество называется субнормальным (нормальным), если mах(mА(х))<1, хÎО (мах(mА(х))=1, хÎО).
Множество уровня А(a) нечеткого множества А есть четкое множество вида А(a)={хÎО: mА(х)£ a}, при этом А(a) монотонно по aÎ[0,1], то есть a1³a2 ÞА(a1)ÌА(a2). Нечеткое множество определяется своими множествами уровня А(a) в виде А=SaiА(ai), 0 < ai £ 1, i=1, 2, …, n, где S понимается как операция суммы нечетких множеств; aiА(ai) – субнормальное четкое множество, для которого maА(a)(х)=a mА(х), " хÎО, что эквивалентно maА(a)(х)=a для хÎ А(a), maА(a)(х)=0 для хÏА(a).
Нечеткие отношения. Пусть Х и Y – два множества элементов х и у произвольной природы (например, Х и Y принадлежат Rn).
Нечеткое бинарное отношение определяется как нечеткое множество S={((x,y), mS(х,y))}, где (x,y) Î Х´Y. Аналогично определяется n-арное отношение S={((x1, x2, … xn), mS(x1, x2, … xn))}, где (x1, x2, … xn) Î Х1 ´ Х2 ´ ´… ´ Хn. Величина mS(х,y) рассматривается как сила (степень) отношения S между х и у.
Поскольку нечеткое отношение определяется как нечеткое множество, могут быть определены операции над нечеткими отношениями, аналогичные соответствующим операциям над нечеткими множествами. Рассмотрим некоторые из них.
Пусть на множестве Х заданы два нечетких отношения А и В, то есть в декартовом произведении Х´X заданы два нечетких множества А и В. Нечеткие множества С = АÈВ и D = АÇВ называются соответственно объединением и пересечением нечетких отношений А и В на множестве Х. При этом функции принадлежности этих отношений запишутся следующим образом:
mС(х) = mах{mА(х,y), mВ(х,y)},
mD(х) = min{mА(х,y), mВ(х,y)}.
Говорят, что нечеткое отношение В включает в себя нечеткое отношение А, если для нечетких множеств А и В выполнено АÍВ. Для функций принадлежности этих множеств неравенство mА(х,y) £ mВ(х,y) выполняется при любых х, y Î X.
Если R – нечеткое отношение на множестве Х, то нечеткое отношение, характеризующееся функцией принадлежности (х,y)=1-mR(х,y); х, yÎX, называется дополнением в X отношения R. Дополнение имеет смысл отрицания исходного отношения. Например, для нечеткого отношения R = (лучше) его дополнение = (не лучше).
Обратное к R нечеткое отношение R-1 на множестве Х определяется следующим образом: xR-1y Û yRx при любых х, y Î X, или с помощью функции принадлежности:
(х, y) = mR(y, x); х, y Î X.
Важное значение в прикладных задачах имеет произведение, или композиция нечетких отношений.
В отличие от обычных отношений это произведение можно определить различными способами.
Максминной композицией (max-min композицией) нечетких бинарных отношений S1 и S2 называется нечеткое отношение S1°S2, для которого функция принадлежности определяется в виде (для хÎХ и zÎZ)
m S1°S2 (х,z) = sup min [mS1(х,y), mS2(y,z)], yÎY.
Минмаксной композицией (min-max композицией) нечетких бинарных отношений S1 и S2 называется нечеткое отношение S1°S2, для которого функция принадлежности определяется в виде (для хÎХ и zÎZ)
m S1°S2 (х,z) = inf max [mS1(х,y), mS2(y,z)], yÎY.
Композиция нечетких отношений обладает свойствами:
S1°(S2°S3) = (S1°S2°)S3,
S1°(S2ÈS3) = (S1°S2)È(S1°S3),
S1ÌS2 = S3°S1Ì S3°S2.
Свойства нечетких отношений:
– рефлексивность; нечеткое отношение S на множестве X называется рефлексивным, если для любого хÎX выполнено равенство mS(х, x) = 1;
– антирефлексивность; функция принадлежности антирефлексивного нечеткого отношения обладает свойством mS(х, x)=0 при любом хÎX;
– симметричность; нечеткое отношение S на множестве X называется симметричным, если для любых х, y Î X выполнено равенство mS (х, y) = mS (y, x);
– антисимметричность; функция принадлежности антисимметричного нечеткого отношения обладает свойством mS(х, y) > 0 Þ mS(y, x) = 0;
– транзитивность; нечеткое отношение S на множестве X называется транзитивным, если S°S Í S.
Свойство транзитивности нечеткого отношения зависит от способа определения произведения нечетких отношений. Если обозначить через S12 и S22 максминное и минмаксное произведение отношения S само на себя, то нетрудно увидеть, что при любых х, y, zÎX выполняется неравенство max[mS(х, y), mS(y, z)] ³ min[mS(х, y), mS(y, z)], отсюда следует, что S12 Í S22.
Всюду ниже под транзитивностью нечеткого отношения мы будем понимать максминную транзитивность, то есть считать, что при любых х, y Î X функция принадлежности транзитивного нечеткого отношения S на множестве X удовлетворяет неравенству
mS(х, z) ³ sup min [mS(х, y), mS(y, z)].
Нечеткие бинарные отношения предпочтения во множестве альтернатив
Информация о ситуации, на основе которой одни альтернативы можно предпочесть другим, может быть задана различными способами. Одним из таких способов является описание информации в форме отношения предпочтения на множестве альтернатив.
Такое отношение может быть выявлено путем консультаций с техническим персоналом – операторами, технологами, являющимися экспертами в данном технологическом процессе. При этом имеется в виду, что эксперты обладают такими знаниями об исследуемом объекте, которые не могут быть формализованы в модели в силу чрезмерной сложности их формализации или по другим причинам [4, 5].
Допустим, что выявлено нечеткое отношение нестрогого предпочтения R на множестве допустимых альтернатив X. Это значит, что относительно любой пары альтернатив x, yÎX высказано одно из трех предположений:
– x не хуже y, то есть (x, y)Î R;
– y не хуже x, то есть (y, x)Î R;
– x и y не сравнимы между собой, то есть
(x, y)Ï R и (y, x)Ï R. (1)
Информация, представленная в таком виде, позволяет сузить класс рациональных выборов, включив в него только те альтернативы, которые не доминируются ни одной альтернативой множества X.
Для того чтобы пояснить, какие альтернативы считаются недоминируемыми, выделим соответствующие отношению предпочтения R отношение строгого предпочтения RD и отношение безразличия RI. Будем говорить, что альтернатива x строго лучше альтернативы y, если одновременно (x, y)Î R и (y ,x)Ï R. Совокупность таких пар и назовем отношением строгого предпочтения RD на множестве X [4]. Воспользуемся определением обратного отношения: (x, y)ÎR-1 Û (y, x)ÎR.
Тогда отношение строгого предпочтения можно записать в следующей форме:
RD = R \ R-1. (2)
Соответствующее R отношение безразличия RI определяется следующим образом. Пара (x, y)Î RI тогда и только тогда, когда либо (x, y)Î R и (y, x)Î R, либо (x, y)Ï R и (y, x)Ï R. Иными словами, (x, y)Î RI в том случае, когда имеющаяся информация в форме отношения предпочтения недостаточна для того, чтобы сделать выбор между альтернативами x и y. Отношение RI можно записать в виде
RI = ((X´X) \ (R È R-1)) È (R Ç R-1). (3)
Если (x, y)Î RD, то будем говорить, что альтернатива x доминирует альтернативу y. Альтернативу xÎX назовем недоминируемой во множестве (X, R), если (y, x)Î RD для любой альтернативы yÎX. Иными словами, если x – недоминируемая альтернатива, то во множестве X нет ни одной альтернативы, которая доминировала бы x. Недоминируемые альтернативы в некотором смысле являются неулучшаемыми в множестве (X, R), и их выбор в задаче принятия решений естественно считать рациональным в пределах имеющейся информации [4].
Таким образом, информация в форме отношения предпочтения R позволяет сузить класс рациональных выборов в X до множества недоминируемых (н.д.) альтернатив вида
X Н.Д. = {x | xÎX, (y, x)Ï R \ R-1 " yÎX}. (4)
Ясно, что, чем больше имеется информации о реальной ситуации или процессе, тем ýже отношение безразличия, ýже подмножество XН.Д. и, следовательно, меньше неопределенность в рациональном выборе альтернатив.
При моделировании больших и сложных систем, к числу которых относятся системы диагностики состояний и управления безопасностью химико-технологического процесса (ХТП), возникают ситуации, когда у экспертов нет четкого представления о предпочтениях между парами альтернатив. В таких случаях эксперты затрудняются с полной определенностью утверждать, что, например, альтернатива x не хуже альтернативы y.
Более гибким способом формализации имеющихся у экспертов знаний о реальной ситуации представляется такой, при котором они имеют возможность описывать степень своей убежденности в предпочтениях между альтернативами числами из интервала [0, 1]. В результате с помощью экспертов выявляется нечеткое отношение предпочтения (н.о.п.) во множестве альтернатив.
Эффективность методов принятия решений, основанных на формализме н.о.п., определяется тем, что они позволяют, в отличие от обычных отношений, учитывать интенсивность предпочтения одних вариантов другим, что дает возможность более адекватно описывать предпочтения экспертов.
Нечетким отношением нестрогого предпочтения н.о.п. на X будем называть любое заданное на этом множестве рефлексивное нечеткое отношение. Нечеткое отношение можно понимать как нечеткое подмножество декартова произведения X´X. Имея это в виду, нечеткое отношение предпочтения будем описывать функцией принадлежности mR: X´X ® [0,1], обладающей свойством рефлексивности, то есть mR(x, x) = 1 при любом xÎX.
Функция принадлежности н.о.п. содержательно интерпретируется как степень предпочтительности одной альтернативы над другой.
Рефлексивность н.о.п. отражает тот естественный факт, что любая альтернатива xÎX не хуже самой себя.
По аналогии с обычными отношениями предпочтения по заданному на множестве X н.о.п. R(mR) можно однозначно определить три соответствующих ему нечетких отношения: безразличия – RI(mIR), квазиэквивалентности RЕ(mЕR) и строгого предпочтения RD(mDR):
RI = ((X´X) \ (R È R-1)) È (R Ç R-1); (5)
RЕ = R ÇR-1; (6)
RD = R \ R-1. (7)
Используя определения пересечения, объединения и разности нечетких множеств, получаем выражения для функций принадлежности этих отношений:
mIR(x, y)=max{1–max{mR(x, y), mR(y, x)}, min{mR(x, y), mR(y, x)}}=
=max{min{1–mR(x, y), 1–mR(y, x)}, min{mR(x, y), mR(y, x)}}; (8)
mЕ R(x, y) = min{mR(x, y), mR(y, x)}; (9)
mDR (x, y) = max{mR(x, y) – mR(y, x), 0}. (10)
Рассмотрим основные свойства введенных нечетких отношений RI(mIR), RЕ(mЕR) и RD (mDR) [1, 4, 5]:
RI (mIR) и RЕ(mЕR) рефлексивны. Действительно, mIR(x, x)=mER(x, x)=m R(x, x)=1, поскольку исходное н.о.п. R(mR) рефлексивно.
RI (mIR) и RЕ(mЕR) симметричны. Симметричность означает, что mR(x, y)=mR(y, x). А это следует непосредственно из определения отношений RI (mIR) и RЕ(mЕR). Действительно, рассмотрим RI(mIR)-
-"(x, y) Î RI(mIR) Þ mR(x, y) = mR(y, x) = 0 Ú mR(x, y) = mR(y, x).
RD(mDR) антирефлексивно. Действительно, так как mR(x, x)=1, а mDR (x, y) = max{mR(x, y) –
- mR(y, x), 0} Þ mDR (x, x) = 0 " xÎX.
RD (mDR) антисимметрично. Пусть mDR (x, y) > 0, то есть mR(x, y)-mR(y, x)>0Þ mR(y, x) = 0, что означает антисимметричность.
Покажем теперь, что если исходное отношение R(mR) транзитивно на X, то тем же свойством обладают и отношения RD (mDR) и RЕ(mЕR).
Теорема 1. Если н.о.п. R(mR) на X транзитивно, то транзитивно и соответствующее нечеткое отношение строгого предпочтения RD (mDR) [5].
Доказательство. Допустим, что в условиях теоремы отношение RD (mDR) не является транзитивным. Это означает, что найдутся х, у, z ÎX, для которых выполнено неравенство
mDR(x, y)<min{mDR(x, z), mDR(z, y)}. (11)
Поскольку mDR (x, y) ³ 0 для " x, у ÎX, то, пользуясь определением mDR, получаем из (11):
mDR (x, z) = mR (x, z) - mR (z, x) > 0, (12)
mDR (z, y) = mR (z, y) - mR (y, z) > 0. (13)
а) Допустим, что mR (x, y) £ mR (y, x). Тогда, учитывая транзитивность R(mR), можно записать неравенство
mR (y, x) ³ mR (x, y) ³ min{mR (x, z), mR (z, y)}. (14)
Из транзитивности R(mR) и неравенства (12) следует, что
mR (x, z) > mR (z, x) ³ min{mR (z, y), mR (y, x)}. (15)
Из (14) и (15) получаем
mR (x, z) > min{mR (z, y), mR (x, z)}. (16)
Из (16) Þ mR (x, z) > mR (z, y) (17)
и, следовательно, из (14) можно заключить, что
mR (x, y) ³ mR (z, y). (18)
Далее, поскольку R(mR) транзитивно, то
mR (y, z) ³ min { mR (x, z), mR (z, y) }.
Отсюда, учитывая неравенство (17) и принятое выше допущение о том, что mR (x, y) £ mR (y, x), получаем:
mR (y, z) ³ min { mR (y, x), mR (z, y)} ³ min { mR (x, y), mR (z, y)}. (19)
Из (19) и (18) следует неравенство mR (y, z) ³ mR (z, y), которое противоречит (13).
Таким образом, мы показали, что из (11) следует невозможность неравенства
mR (x, y) £ mR (y, x).
б) Допустим, что mR (x, y) > mR (y, x). Тогда
mDR (x, y) = mR (x, y) - mR (y, x) > 0,
и неравенство (11) можно записать в виде:
mR (x, y) - mR (y, x) < min { [ mR (x, z) - mR (z, x)],
[mR (z, y) - mR (y, z)]}. (20)
Допустим, что mR (y, z) ³ mR (y, x). Тогда в (20) величину mR (y, z) можно заменить на величину
mR (y, x):
mR(x, y)>mR(y, x)<min{[mR(x, z)-mR(z, x)], [mR(z, y)-mR(y, x)]}. (21)
Прибавив mR(y, x) к обеим частям этого неравенства, получим
mR(x, y)<min{[mR(x, z)+(mR(y, x)-mR(z, x))], mR(z, y)}. (22)
Здесь следует рассмотреть две возможности.
Если mR (y, x) - mR (z, x) £ 0, то из (22) получаем неравенство mR(y, x) < min{ mR (x, z), mR (z, y) }, которое противоречит транзитивности R(mR).
Если mR(y, x) - mR (z, x) > 0, то, учитывая транзитивность R(mR), можно записать: mR(y, x) >
mR(z, x) ³ min{mR (z, y), mR (y, x)}, откуда сразу следует неравенство mR(y, x) > mR(z, y), которое противоречит допущению о том, что mR (y, z) ³ mR (y, x), и неравенству (13).
Таким образом, мы показали, что при условии mR(x, y) > mR(y, x) из неравенств (12) и (13) вытекает неравенство
mR(y, z) < mR(y, x). (23)
Рассуждая аналогичным образом, можно показать, что при условии mR(x, y) > mR (y, x) из (12) и (13) вытекает неравенство
mR(z, x) < mR(y, x). (24)
Далее, пользуясь неравенствами
mR(y, z) ³ min{mR (y, x), mR (x, z)},
mR(z, x) ³ min{mR (z, y), mR (y, x)},
из (11) и (12), получаем неравенства:
mR (y, z) ³ mR (x, z), mR (z, x) ³ mR (z, y),
которые, как нетрудно видеть, противоречат неравенствам (12) и (13). Этим противоречием завершается доказательство теоремы 1.
Теорема 2. Если нечеткое отношение предпочтения R(mR) на X транзитивно, то транзитивно и соответствующее нечеткое отношение квазиэквивалентности RЕ(mЕR) [4].
Доказательство. Допустим, что в условиях теоремы отношение RЕ(mЕR) не является транзитивным. По определению транзитивности это допущение означает, что найдутся такие х, у, zÎX, для которых выполнено неравенство
mЕR < min{mЕR (x, z), mЕR (z, y)}. (25)
Допустим теперь, что mR(x, y) ³ mR(y, x) (в противном случае доказательство аналогично). Тогда из определения RЕ(mЕR) получаем, что mЕR(x, y) = mR(y, x). Пользуясь этим равенством, запишем неравенство (25) в виде
mR(y, x) < min{mЕR(x, z), mЕR(z, y)}. (26)
Поскольку RЕ(mЕR) симметрично, то из (26) получаем
mR(y, x) < min{mЕR(y, z), mЕR(z, x)}. (27)
Далее из определения RЕ(mЕR) следует, что mR (y, z) £ mR (y, z), mЕR(z, x) £ mR(z, x), то есть
min{mЕR(y, z), mЕR(z, x)} £ min{mR(y, z), mR(z, x)}. (28)
Из неравенств (27) и (28) заключаем, что
mR(y, x) < min{mR(y, z), mR(z, x)}. (29)
Последнее неравенство противоречит условию транзитивности исходного н.о.п. R(mR). Этим противоречием завершается доказательство теоремы.
Из рассмотренной теоремы и приведенных выше свойств отношения RЕ(mЕR) следует, что в условиях теоремы 2 RЕ(mЕR) представляет собой нечеткое отношение эквивалентности (рефлективное, симметричное, транзитивное).
Обычное рефлексивное и транзитивное отношение на множестве X называется квазипорядком на X, а антирефлексивное, антисимметричное и транзитивное отношение называется строгим порядком на X [6].
Пользуясь этой терминологией и проводя аналогию с обычными отношениями, приведенные теоремы 1 и 2 можно сформулировать следующим образом [4].
Теорема 3. Если R(mR) – нечеткий квазипорядок на множестве X, то RD(mDR) – соответствующий нечеткий строгий порядок на X, а RЕ(mЕR) – соответствующее нечеткое отношение эквивалентности.
Линейность нечетких отношений
Определение 1. Отношение R на X называется линейным, если этим отношением или обратным к нему отношением связаны любые две альтернативы данного множества. Иными словами, при линейном отношении на множестве X нет не сравнимых между собой по предпочтению альтернатив.
Нетрудно понять, что линейность обычного отношения эквивалентна условию: R È R-1 = X´X. Это условие можно записать в виде:
mR(x, y) = 0 Þ mR(y, x) = 1.
В случае нечеткого отношения однозначно можно определить лишь полное отсутствие линейности: нечеткое отношение не является линейным тогда и только тогда, когда найдутся такие альтернативы x, yÎX, для которых выполнено равенство mR(x, y)=mR(y, x)=0, где mR(x, y) – функция принадлежности данного нечеткого отношения.
Свойство линейности нечеткого отношения можно понимать более широко, чем в случае обычного отношения, в силу того, что функция принадлежности такого отношения может принимать, кроме 0 и 1, любые промежуточные значения. Пользуясь этим, можно ввести понятие степени линейности отношения.
Определение 2. Пусть l – некоторое число из интервала [0, 1]. Нечеткое отношение R(mR) называется l-линейным, если его функция принадлежности удовлетворяет условию max{mR(x, y), mR(y, x)}>l при любых x, y ÎX.
Таким образом, если нечеткое отношение предпочтения является, например, 0,7-линейным, то из каждых двух альтернатив по крайней мере одна не хуже другой со степенью, большей 0,7.
Определение 3. Нечеткое отношение R(mR) называется сильно линейным, если его функция принадлежности удовлетворяет условию max{mR(x, y), mR(y, x)} = 1 при любых x, yÎX.
Иначе свойство сильной линейности можно определить следующим образом:
mR(x, y) ³ mR(y, x) Þ mR(x, y) = 1 (30)
при любых x, yÎX.
Чтобы пояснить смысл свойства сильной линейности, покажем, что оно эквивалентно условию
mR(x, y) = 1 - mDR(y, x) для "x, yÎX, (31)
где RD(mDR) – соответствующее нечеткое отношение строгого предпочтения. Действительно, если выполнено (30), то по определению mDR получаем mDR(y, x)=0, то есть условие (31) также выполнено. Если же выполнено (31) и mR(x, y)³mR(y, x), то mDR(y, x)=0 и mR(x, y)=1, то есть выполнено (30).
Условие сильной линейности в форме (31) можно записать в виде
R-1 = (X´X) \ RD. (32)
Смысл (32) можно пояснить следующим образом. Если, например, альтернативы х и у таковы, что x доминирует у со степенью 1, то (y, x)ÏR-1, то есть альтернатива у не доминирует x ни с какой положительной степенью.
Если же (x, y)ÏRD, то (y, x)ÎR-1, то есть у доминирует x со степенью 1.
Если, наконец, x доминирует у со степенью a, то со степенью 1-a выполнено предпочтение (y, x)ÎR. Таким образом, по своему смыслу сильная линейность в наибольшей степени аналогична свойству линейности обычного отношения.
Из определения сильной линейности следует, что при сильно линейном нечетком отношении R на множестве X для любых двух альтернатив x1, x2 выполнено по крайней мере одно из равенств:
mR(x1, x2)=1, mR(x2, x1)=1.
Еще одно свойство сильно линейного нечеткого отношения состоит в том, что соответствующие ему нечеткие отношения RЕ(mЕR) и RI(mIR) совпадают. Действительно, допустим, что для некоторой пары
(x, y)ÎX выполнено mR(x, y)³mR(y, x). Тогда из определения 3 следует, что mR(x, y)=1, а из определения RI(mIR) получаем, что mIR(x, y)=mR(y, x). В силу симметричности RI(mIR) в случае mR(x, y)£mR(y, x) имеем mIR(x, y)=mR(x, y), и, следовательно:
mIR(x, y) = min{mR(x, y), mR(y, x)} = mЕR(x, y). (33)
Определение 4. Нечеткое отношение R(mR) называется 0-линейным или слабо линейным, если его функция принадлежности удовлетворяет условию mR(x, y)=0 Þ mR(y, x)>0 при любых x, yÎX.
Центр безопасности
Основной задачей промышленных систем диагностики является своевременное обнаружение нарушений, которые приводят к внештатным ситуациям. Для того чтобы иметь возможность выявить возможное нарушение на ранней стадии его развития, необходима количественная оценка безопасности.
В данной работе предлагается метод определения области центра безопасности (ЦБ) для ХТП, то есть такой области, в которой данный процесс является наиболее безопасным во время его рабочего (штатного) функционирования.
Функционирование любого ХТП можно рассматривать как последовательность смены состояний на некотором интервале времени (to, tk). Состояние XТП в каждый момент времени tÎ(to, tk) характеризуется набором параметров: Y={Ti, Kj, Ul}, где {Ti, i=1…I} – параметры состояния технологии процесса;
{Kj, j=1…J} – параметры состояния оборудования процесса; {Ul, l=1…L} – параметры состояния систем управления процессом.
На ХТП могут быть наложены ограничения штатного функционирования , зависящие от множеств параметров {Ti, Kj, Ul}. Выход за эти ограничения означает переход ХТП во внештатную ситуацию. Таким образом, эти ограничения разделяют пространство всех состояний, в которых может находиться ХТП, на два множества: опасных состояний и безопасных (работоспособных) состояний. Во множестве безопасных состояний наибольший интерес представляет область, в которой функционирование ХТП является наиболее безопасным, – область центра технологической безопасности.
Рассмотрим методику определения ЦБ для технологических параметров ХТП. Данная методика основывается на том, что информация о состояниях ХТП, на основе которой принимается решение о выборе ЦБ, представляется в виде н.о.п. во множестве альтернатив выбора.
На первом шаге определяется конечное множество альтернатив, на котором строится н.о.п. Для этого для каждого из технологических параметров ХТП в области его существования выделяются интервалы – диапазоны значений параметров, характеризующих определенные режимы работы технологии, то есть соответствующие определенным состояниям ХТП. Таким образом, получаем ограниченное множество непересекающихся интервалов {xTpKp}, здесь Tp – индекс технологического параметра, Kp – индекс интервала данного технологического параметра.
Далее на множестве непересекающихся интервалов значений технологического параметра Р задается нечеткое отношение нестрогого предпочтения R(mR) с функцией принадлежности mR(x1, x2), показывающее, какой из двух интервалов более предпочтителен с точки зрения безопасности: x1 или x2. Это отношение выявляется с помощью знаний экспертов (технологов, операторов), которые проводят попарно нечеткое сравнение на множестве интервалов значений параметра и определяют степень принадлежности mR(x1, x2), интерпретируемое следующим образом: «интервал x1 значений параметра P не опаснее интервала x2 значений параметра P».
Равенство mR(x1, x2)=0 может означать либо то, что с положительной степенью выполнено обратное предпочтение, то есть mR(x2, x1) > 0, либо то, что альтернативные состояния s1 и s2 несравнимы между собой ни с какой положительной степенью, то есть и mR(x2, x1)=0. Как было показано выше, н.о.п. является рефлексивным, в данном случае это отражает тот факт, что любой интервал не опаснее самого себя, таким образом, в силу рефлективности имеем mR(x1, x1)=0.
Для того чтобы выделить те интервалы параметров, которые считаются недоминируемыми, выделим соответствующее отношению предпочтения R отношение строгого предпочтения RD. Будем говорить, что интервал x1 строго безопаснее интервала x2, если одновременно (x1, x2)ÎR и (x2, x1)ÏR. Совокупность таких пар назовем отношением строгого предпочтения на X и будем использовать его для определения и анализа свойств множества недоминируемых альтернатив, то есть таких альтернатив, выбор которых является наилучшим в заданном множестве, пару (X, R(mR)) назовем моделью выбора. Этот выбор представляет подмножество наиболее безопасных интервалов для некоторого технологического параметра. Отношение строгого предпочтения получаем как разность отношения нестрогого предпочтения R и обратного к нему отношения R-1, таким образом, функция принадлежности отношения RD вычисляется через разность нечетких множеств [4].
Как было показано выше, RD=R\R-1, где R-1 – обратное к R отношение, описываемое функцией принадлежности: .
Функция принадлежности разности двух нечетких множеств А\В записывается в следующем виде [4]:
. (34)
Тогда нечеткое отношение доминирования RD описывается следующей функцией принадлежности:
. (35)
Для четкого случая альтернатива x называется недоминируемой, если для любого yÎX (y, x) Ï RD, то есть не существует альтернативы, которая доминировала (была строго предпочтительнее) x. В случае нечеткого отношения доминирования для любой альтернативы x величина (являющаяся значением функции принадлежности дополнения отношения RD) показывает степень, с которой альтернатива x не доминируется альтернативой y.
Тогда величина показывает степень недоминируемости альтернативы x1. Это позволяет сформулировать понятие нечеткого множества , определяемого функцией принадпринадлежности вида:
(36)
которое называется нечетким множеством недоминируемых альтернатив в модели выбора (X, R(mR)).
С учетом (35) получим:
. (37)
Таким образом, нечеткое множество ставит в соответствие каждой альтернативе xÎX степень ее недоминируемости, принимающую значения от 0 до 1. Чем больше степень принадлежности альтернативы x нечеткому множеству , тем более предпочтительной является данная альтернатива.
Поскольку величина есть степень «недоминируемости» интервала параметра x, рациональным при заданной нечеткой информации естественно считать выбор тех интервалов, которые имеют по возможности наибольшую степень принадлежности нечеткому множеству , то есть тех, которые дают значение , по возможности более близкое к величине
. (38)
Интервалы значений некоторого технологического параметра, дающие в точности эту величину, называются максимально недоминируемыми альтернативами модели выбора (X, R(mR)):
. (39)
Таким образом, выделив из полученного нечеткого множества интервал, имеющий максимальную степень недоминируемости, получаем интервал ti0, который является наиболее предпочтительным для данного технологического параметра с точки зрения безопасности.
Проделав эту процедуру для всех технологических параметров процесса, получим набор интервалов, которые характеризуют состояние области ЦБ для технологических параметров: S0={t10, t20, …, tn0}, где ti0 – ЦБ для i-го параметра.
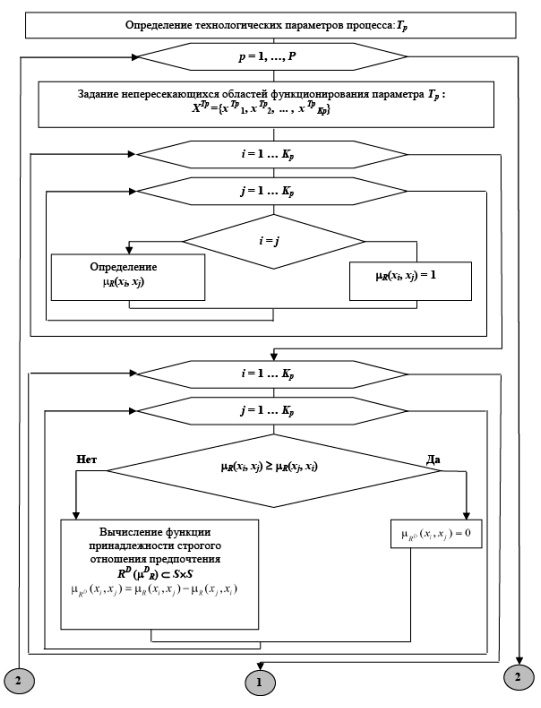
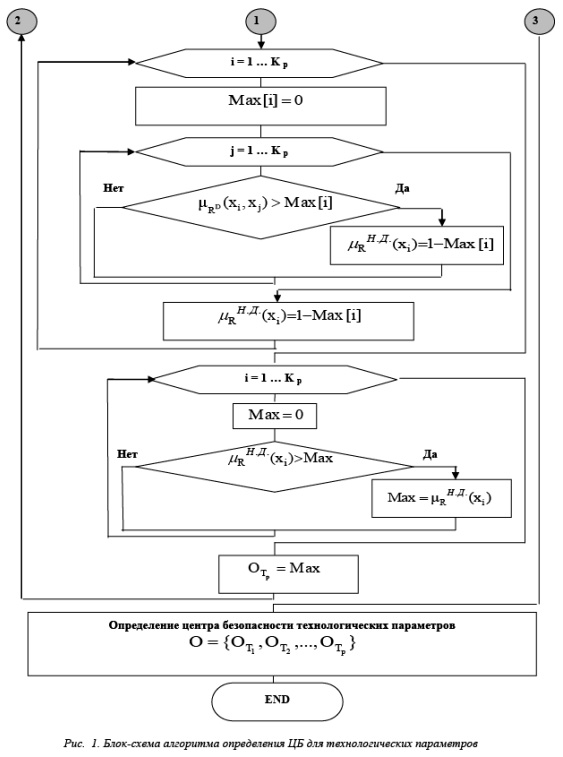
Блок-схема алгоритма определения ЦБ для технологических параметров приведена на рисунке 1.
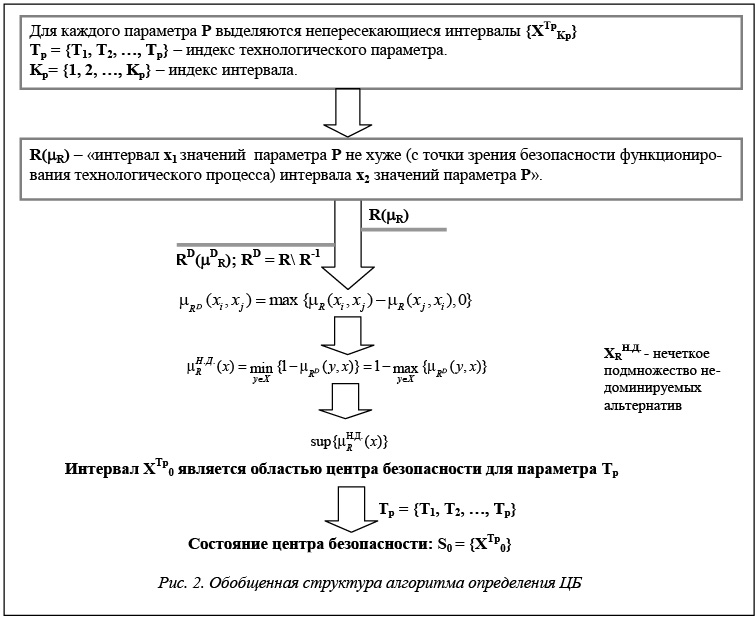
На рисунке 2 приведена обобщенная структура алгоритма определения ЦБ для технологических параметров ХТП.
Для определения ЦБ состояния оборудования и систем управления технологического процесса проводится динамический анализ статистических данных о наработке на отказ оборудования и систем управления, по которым строится вероятностная оценка отказов оборудования и систем управления. Вероятность отказа в пределах от 0 до 5 процентов определяется как ЦБ.
Индекс безопасности
Выделение центра технологической безопасности позволяет численно определять смещение рабочей точки процесса от ЦБ – наиболее безопасного состояния процесса.
В процессе работы ХТП в результате изменения его параметров происходит постоянная смена состояний и вследствие этого выход из области ЦБ. Оценить этот выход можно с помощью определения смещения от ЦБ. Количественная характеристика удаленности текущей рабочей точки процесса s* от точки, определяющей ЦБ so (рис. 3), покажет степень безопасности для данного состояния ХТП.
В работе эта количественная характеристика определена как индекс безопасности. Приведем обозначения и формулы, используемые на рисунке 3:
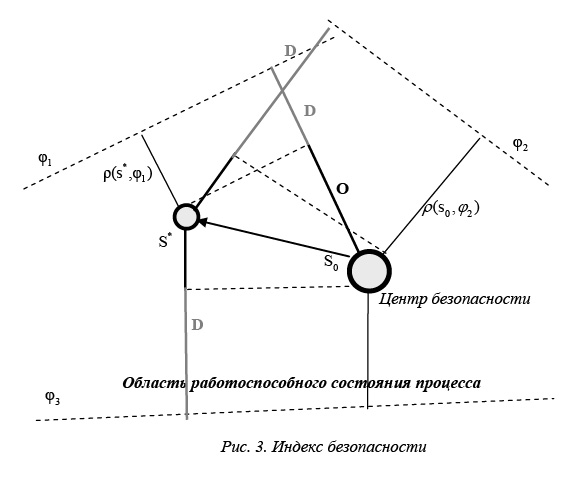
S – множество всевозможных состояний процесса;
Sр – множество работоспособных состояний процесса;
– множество границ области работоспособного состояния (вырезает на S множество Sр);
so – точка процесса, соответствующая центру безопасности для данного процесса;
s* – текущая рабочая точка процесса;
– расстояние от рабочей точки процесса s* до границ области работоспособного состояния ji;
– расстояние от рабочей точки процесса s* до центра безопасности so относительно границ;
– расстояние от центра безопасности so до границ области работоспособного состояния ji;
– степень опасности для данного состояния s* ХТП относительно границ ;
– степень безопасности для данного состояния s* ХТП относительно границ .
Методика определения индекса безопасности
Пусть T = {T1, T2, …, Tp} – множество технологических параметров, которыми описывается некоторое состояние ХТП. Набор значений параметров, описывающих такое состояние в некоторый момент времени, назовем ситуацией. Множество всевозможных ситуаций, возникающих в результате функционирования ХТП, может использоваться для формирования решающей таблицы, то есть соответствия между ситуацией и набором управляющих решений. Размер такой решающей таблицы определяется числом ситуаций, которое, в свою очередь, зависит от степени конкретизации значений, набора параметров, характеризующих данный ХТП. Размерность решающей таблицы может быть уменьшена за счет выделения типовых ситуаций, на которых может быть сосредоточено внимание экспертов.
При описании таких ситуаций эксперту наиболее удобно пользоваться словесными значениями параметров. Для формализации такого представления используется понятие лингвистической переменной, которая задается на некоторой количественной шкале и принимает значения, являющиеся словами естественного языка. Такие переменные служат для качественного словесного описания некоторой количественной величины, с их помощью формализуется качественная информация, представленная в словесной форме. Поставим в соответствие каждому параметру ХТП лингвистическую переменную <βi, Ei, Di>, где βi – название лингвистической переменной; Ei={E1i, E2i, ..., EMii} – терм-множество лингвистической переменной βi; Di – базовое множество лингвистической переменной βi; каждому элементу терм-множества Ei ставится в соответствие своя функция принадлежности (рис. 4).
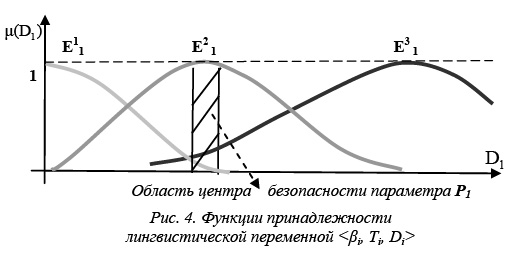
Для описания термов Eij, соответствующих значениям βi, используются нечеткие переменные, то есть каждый терм описывается нечетким множеством в базовом множестве данной лингвистической переменной. Множество, состоящее из набора лингвистических переменных βi, представляющих параметры ХТП, нечетко определяет некоторое состояние технологического процесса. Такое множество назовем нечеткой ситуацией. Например, возможна следующая нечеткая ситуация, возникшая в процессе функционирования некоторого типового ХТП:
{<<0,8/«Хорошая»>, <0,18/«Плохая»>, /«Концентрация раствора на входе в аппарат»>, <<0,7/«Хорошая»>, <0,25/«Плохая»>, /«Концентрация раствора на выходе из аппарата»>, <<0,9/«Нормальное»>, <0,15/«Плохое»>, <0,01/«Опасное»>, /«Давление пара на входе в аппарат»>, …}.
Дадим формальное определение нечеткой ситуации. Пусть Tp={T1, T2, …, Tp} – множество параметров, значениями которых описывается состояние процесса. Каждый параметр Ti описывается соответствующей лингвистической переменной <βi, Тi, Di>. Нечеткой ситуацией называется нечеткое множество второго уровня:
,
где μs(Ti)={<μμs(Ti)( / )>}; j=1…Mi; i=1…Tp.
Типовые нечеткие ситуации могут использоваться для идентификации некоторой входной нечеткой ситуации по степени их близости. В качестве меры близости между ситуациями рассматриваются два критерия: степень нечеткого включения и степень нечеткого равенства. Эти понятия базируются на определении степени нечеткого включения и степени нечеткого равенства нечетких множеств [7], например, пусть и есть некоторые нечеткие ситуации.
Степень включения ситуации в ситуацию обозначается и определяется выражением:
, где
,
. (40)
Для ограничения возможных вариантов альтернатив, возникающих при диагностике ХТП, будем считать, что ситуация нечетко включается в , , если степень включения в не меньше некоторого порога включения tincÎ[0,6; 1], определяемого условиями управления, то есть . Другими словами, ситуация нечетко включается в ситуацию , если нечеткие значения признаков ситуации нечетко включаются в нечеткие значения соответствующих признаков ситуации . Фиксация порога включения в некоторой точке интервала [0,6; 1] зависит от особенностей объекта управления, требований к качеству управляющих решений и т.д.
Пусть есть некоторое множество типовых ситуаций. Назовем нечеткое отношение , где , отношением нечеткого включения, если . Справедлива следующая теорема [7].
Теорема 4. Отношение нечеткого включения есть отношение нечеткого нестрогого порядка.
Если множество текущих ситуаций S содержит такие ситуации и (i, j Î K = {1, 2, ..., N}, i ¹ j), что нечетко включается в , а нечетко включается в , то ситуации и нужно воспринимать как одну ситуацию. Это означает, что при данном пороге включения tinc ситуации и примерно одинаковы. Такое сходство ситуаций называется нечетким равенством, при этом степень нечеткого равенства
. (41)
Считается, что ситуации и нечетко равны, , если , где tinc Î [0,6; 1] – порог нечеткого равенства. Естественно, что , если нечеткие значения соответствующих параметров в ситуациях и нечетко равны, то есть .
Пусть есть некоторое множество типовых ситуаций. Назовем нечеткое отношение , где , отношением нечеткого равенства, если . Справедлива следующая теорема [7].
Теорема 5. Отношение нечеткого равенства есть отношение нечеткой эквивалентности.
На основании теоремы 4 множество Ss типовых ситуаций можно разбить на классы нечеткой эквивалентности, причем в один класс будут входить нечетко равные между собой ситуации. Следовательно, в пределах достоверности, ограничиваемых порогом нечеткого равенства t, все ситуации одного класса эквивалентности можно считать одной ситуацией, которая получается нечетким объединением ситуаций, принадлежащих классу . Полученная ситуация может использоваться при идентификации входной ситуации посредством сравнения ее с ситуациями из S на нечеткое равенство.
Для определения индекса безопасности в качестве типовой нечеткой ситуации достаточно иметь одну нечеткую ситуацию, которая характеризует центр технологической безопасности. Обозначим эту ситуацию .
Таким образом, для определения индекса безопасности для текущего состояния процесса необходимо сравнить на нечеткое равенство входную нечеткую ситуацию с нечеткой ситуацией, которая характеризует центр безопасности . При этом степень нечеткого равенства
(42)
и покажет величину, определенную как индекс безопасности ХТП.
Блок-схема алгоритма расчета индекса безопасности приведена на рисунке 1.
Расчет индекса безопасности для группы аппаратов
Рассмотрим расчет индекса безопасности для нескольких аппаратов, составляющих в совокупности ХТС группы аппаратов.
Пусть ХТС состоит из R аппаратов, для каждого из которых рассчитан свой индекс безопасности Di, который показывает степень удаленности рабочей точки процесса от ЦБ.
Рассмотрим множество {D1, D2, D3, …, DR}, состоящее из индексов безопасности для каждого из процессов ХТС. Совокупность этих индексов определяет состояние всей системы.
Для расчета индекса безопасности для группы аппаратов применим следующую методику.
Поставим каждому индексу безопасности Di(iÎI={1, 2, ..., R}) в соответствие лингвистическую переменную <λi, Ei, Xi>, где λi – название переменной – «оценка состояния i-го аппарата»; Ei={E1i, E2i, ..., EMii} – терм-множество лингвистической переменной λi; Xi – базовое множество лингвистической переменной λi.
Таким образом, перейдем от индекса безопасности Di для i-го аппарата к оценке состояния этого аппарата по его индексу безопасности, для этого необходимо построить терм-множества лингвистической переменной λi (рис. 5).
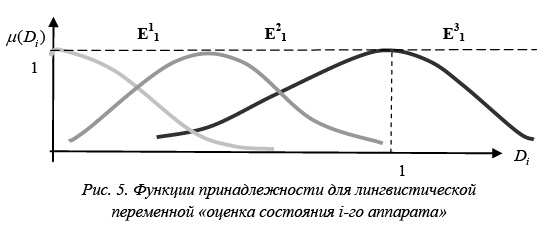
Для описания термов Тij(jÎH={1, 2, ..., Mi}), соответствующих значениям βi, используются нечеткие переменные , то есть Тij описывается нечетким множеством в базовом множестве Di:
,
где – степень принадлежности элемента d нечеткому множеству .
Далее применяем методику, аналогичную рассмотренной выше.
Пусть D={D1, D2, …, DR} – множество индексов безопасности, значениями которых описывается состояние всей технологической системы. Каждый индекс безопасности описывается соответствующей лингвистической переменной <λi, Ei, Xi>.
Индекс безопасности для группы аппаратов рассчитаем как степень нечеткого равенства некоторой текущей ситуации , определяющей состояние всей системы с ситуацией, которая определяет центр безопасности для всей системы .
Таким образом, для определения индекса безопасности для всей системы необходимо сравнить на нечеткое равенство входную нечеткую ситуацию с нечеткой ситуацией, которая характеризует ЦБ . При этом степень нечеткого равенства покажет индекс безопасности всей системы.
Построение области безопасного функционирования технологического процесса
Выше была описана методика определения ЦБ как наиболее предпочтительного состояния ведения процесса с точки зрения безопасности. Используя понятия центр и индекс безопасности, введенные в предыдущих разделах, можно выделить область безопасного функционирования (ОБФ) ХТП на множестве всех возможных состояний.
ОБФ ХТП представляет собой подмножество состояний на конечном множестве диапазонов значений параметров, характеризующих определенные режимы работы ХТП, то есть состояния технологии. В это множество будут входить те состояния, которые являются безопасными с точки зрения ведения технологического процесса, но не совпадают с центром безопасности. Рассмотрим метод нахождения области безопасного функционирования ХТП.
Пусть для некоторого объекта технологического процесса определен ЦБ по всем технологическим параметрам (S0 = {t10 , t20 , …, tn0}, t i0 – ЦБ для i-го параметра) и существует набор нечетких типовых состояний si~ Î S~ (i Î 1, 2, …, N), определенных при помощи экспертного опроса по разработанным алгоритмам (рис. 6, 7). Тогда из множества всех типовых состояний ХТП можно выделить некоторое подмножество состояний sbj~ Î S~, которые принадлежат к безопасным состояниям функционирования ХТП, но не совпадают полностью с определенным ЦБ. Существование таких состояний обусловлено тем, что данные состояния могут отклоняться от ЦБ только по одному или нескольким значениям технологических параметров или отклонения по технологическим параметрам могут быть незначительными (то есть в пределах значения порога нечеткого включения состояний tincÎ[0,6; 1]). Выявленный набор таких состояний будет представлять собой область безопасного функционирования ХТП.
Таким образом, в ОБФ, кроме самого ЦБ, войдут все состояния sbj~ Î S~, для которых значение степени принадлежности определяющих их интервалов нечеткому множеству будет не менее установленного порога tinc в модели выбора (X, R(mR)), то есть для каждого интервала x, определяющего состояние, входящее в область безопасного функционирования, должно выполняться неравенство , где .
Следуя этой методике, можно выделить подмножество состояний Sbj={t1j , t2j , …, tnj}, где t ij – интервалы i-го параметра j-го состояния (j=1…k), удовлетворяющие условию .
Для практического нахождения состояний, удовлетворяющих описанным выше условиям для конкретного объекта ХТП, в разработанной информационной системе используется следующая методика.
- Выявить набор параметров, по которым будет оцениваться ЦБ для данного объекта ХТП.
- Построить функции и определить степени принадлежности соответствующим лингвистическим переменным для каждого из выявленных параметров для дальнейшего вычисления степеней нечеткого включения и нечеткого равенства состояний.
- Вычислить степени нечеткого включения значений технологических параметров типового состояния в ЦБ.
- Вычислить степени нечеткого включения значений технологических параметров ЦБ в типовое состояние.
- Рассчитать степень нечеткого равенства между типовым состоянием и ЦБ на основе полученных степеней включения.
- Состояния, степень нечеткого равенства которых будет удовлетворять определенному условию (tincÎ [0,6; 1]), будут представлять собой область безопасного функционирования объекта.
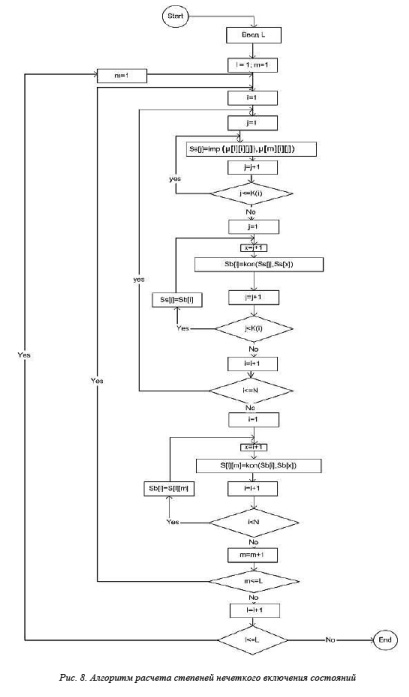
На рисунке 6 приведена блок-схема алгоритма, позволяющего при помощи эксперта перечислить все типовые состояния объекта ХТС, по которым делается диагностика. Далее на множестве типовых состояний задаются функции и значения степеней принадлежности для каждого выделенного интервала каждого из рассматриваемых параметров объекта ХТС. Эта процедура реализуется алгоритмом, блок-схема которого представлена на рисунке 7. Следующая задача – расчет степеней нечеткого включения интервалов состояний друг в друга – решается алгоритмом, показанным на рисунке 8. Для выявления нечетко равных состояний используется алгоритм расчета степеней нечеткого
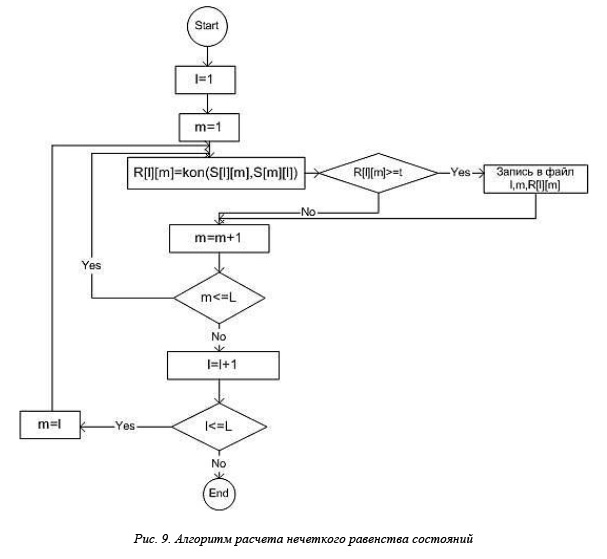
равенства состояний. Значения степеней нечеткого равенства состояний рассчитываются по алгоритму, показанному на рисунке 9, на основе значений степеней нечеткого включения, полученных на предыдущем шаге.
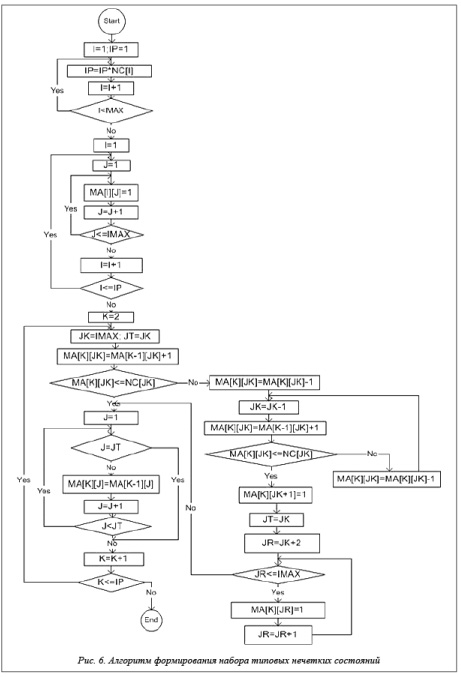
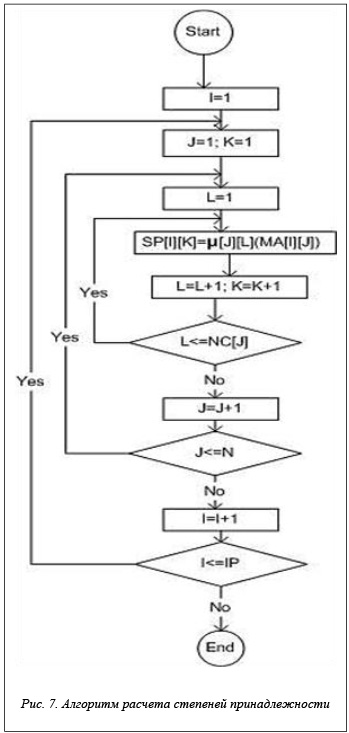
Основные обозначения и сокращения, применяемые при построении блок-схемы на рисунках 6 и 7: NC[I] – количество режимов работы (термов) признака I; IMAX – количество рассматриваемых признаков;
I – номер строки (состояния) в MA[I][J];
J – номер признака в MA[I][J]; I – номер состояния; J – номер признака; K – «абсолютный» номер режима работы; L – номер функции принадлежности признака J; SP[I][K] – степень принадлежности режима работы K состоянию I; μ[J][L](MA[I][J]) – значение функции принадлежности признака J с номером L; NC[J] – количество режимов работы признака J; N – количество признаков; IP – количество состояний.
Основные обозначения и сокращения, применяемые при построении блок-схемы на рисунках 8 и 9: L – количество состояний; l – номер сравниваемого состояния; m – номер сравниваемого состояния; i – номер признака; j – номер режима работы; K(i) – количество режимов работы признака i; S[l][m] – значение степени нечеткого включения состояний; R[l][m] – значение нечеткого равенства состояний; t – порог нечеткого равенства.
Таким образом, используя представленные алгоритмы 1–4, можно определить набор состояний, входящих в область безопасного функционирования ХТП. Фактически к ним будут относиться все состояния, степень нечеткого равенства которых не меньше некоторого определенного порога включения
tinc Î [0,6; 1], определяемого условиями управления, то есть ≥ tinc, где si~ – текущее состояние ХТП, а S0 – ЦБ.
Выделенная таким образом область безопасного функционирования ХТП используется на втором уровне диагностической модели.
Качественная модель развития опасностей на основе нечетких бинарных отношений
Рассмотрим качественную модель развития опасностей на основе нечеткого бинарного отношения предпочтения. Это отношение строится на множестве опасностей О: О={о1, о2, о3, …, оn}, где оi – i-я опасность возникновения нештатной ситуации для данного ХТП, n – мощность множества О. Обозначим это отношение через со степенью принадлежности и интерпретируем его как «опасность оi порождает опасность оj», где оi ,оj Î О. То есть запись означает, что опасность оi порождает опасность оj со степенью принадлежности . Представим отношение в виде матрицы и в виде нечеткого графа развития опасностей , в котором вес дуги, направленной от оi к оj , равен . Такие взаимосвязи показывают нечетко определенный сценарий развития нештатных ситуаций.
Построение качественной модели развития опасностей рассмотрим на примере ХТП выпаривания электролитических щелоков. В качестве нештатной ситуации выступает опасность О0 – нарушение работы первого выпарного аппарата. Остальные опасности, например: О1 – неисправность системы регулирования расхода греющего пара; О2 – неисправность датчика расхода греющего пара и т.д., являются возможными причинами возникновения нарушения О0.
Далее приведены перечень опасностей технологического процесса, их коды и описание:
о0 – нарушение работы первого выпарного аппарата;
o1 – неисправность системы регулирования расхода греющего пара;
o2 – неисправность датчика расхода греющего пара;
o3 – нееисправность регулятора давления греющего пара;
o4 – неисправность клапана на линии подачи греющего пара;
o5 – неисправность вторичного прибора;
o6 – изменение давления в греющей камере;
o7 – изменение давления в парожидкостном пространстве;
o8 – изменение подачи насоса;
o9 – изменение подачи греющего пара;
o10 – нарушение подачи пара в сети;
o11 – разбито смотровое окно;
o12 – течь, нарушение герметичности стыковых фланцев;
o13 – нарушение герметичности аппарата;
o14 – прохудилась труба подачи щелочи;
o15 – уменьшение выхода щелочи;
o16 – забивка трубок греющей камеры;
o17 – нарушение герметичности трубок;
o18 – изменение режима кипения;
o19 – пробулькивание пара в греющей камере;
o20 – изменение концентрации NaOH.
Матрица нечеткого отношения – опасность оi порождает опасность оj для данного примера приведена в таблице, нечеткий граф развития опасностей изображен на рисунке 10.

.jpg)
Далее проводятся анализ и преобразование нечеткого графа развития опасностей, целью которого является выделение в нем иерархической структуры, позволяющей проводить процедуру диагностирования внештатных ситуаций на множестве опасностей.
Для построения иерархической диаграммы диагностирования в графе развития опасностей убираются транзитивно замыкающие дуги и вершины графа разносятся по уровням.
При этом на верхнем, первом уровне иерархии располагаются вершины, из которых не выходит ни одна дуга. На втором уровне иерархии располагаются вершины, из которых выходят дуги, инцидентные только вершинам первого уровня. На некотором i-м уровне иерархии (i£n) располагаются вершины, из которых выходят дуги, инцидентные вершинам, расположенным на уровнях с первого по i-й (рис. 11).
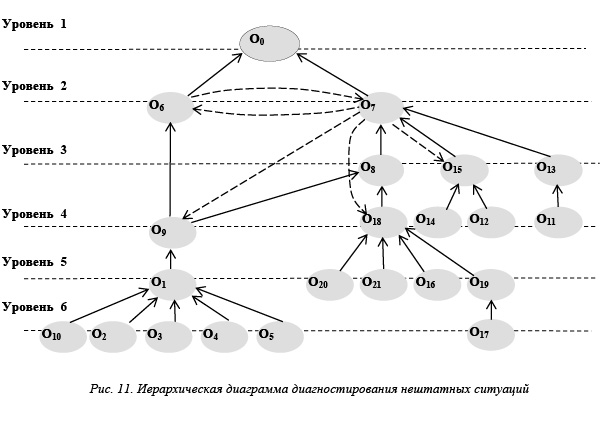
На диаграмме также отображаются циклические связи между опасностями, которые показывают взаимовлияние опасностей друг на друга, непосредственно или через цепочку опасностей. Эти связи не оказывают существенного влияния на дальнейшую процедуру определения первопричины нештатной ситуации, так как главнми целями являются достижение терминальных узлов диаграммы , то есть тех узлов, из которых не исходят дуги, и проверка условий работоспособности или наличия неисправностей. Поэтому мы можем исключить циклические связи из диаграммы , что не повлияет на изменение пространства поиска возможных нарушений. В итоге получаем иерархическую древовидную диаграмму, показывающую возможные сценарии развития внештатных ситуаций .
Каждый сценарий представляет собой множество переходов из оi в оj , где каждому переходу приписана его функция принадлежности , показывающая степень влияния одной опасности на другую.
Возьмем для некоторого сценария среднее значение всех функций принадлежности входящих в него дуг. В результате для некоторого сценария развития опасности получим величину, характеризующую степень его возможности, что позволит ранжировать множество сценариев в процессе процедуры диагностирования.
Литература
- Кофман Ф. Введение в теорию нечетких множеств. М.: Радио и связь, 1982. 433с.
- Трухаев Р.И. Модели принятия решений в условиях неопределенности. М.: Наука, 1981. 258 с.
- Кафаров В.В., Дорохов И.Н. Системный анализ процессов химической технологии. Основы стратегии. М.: Наука, 1976. 500 с.
- Орловский С.А. Проблемы принятия решений при нечеткой исходной информации. М.: Наука, 1981. 208 с.
- Нечеткие множества в моделях управления и искусственного интеллекта; [под ред. Д.А. Поспелова]. М.: Наука, 1986. 396 с.
- Шрейдер Ю.А. Равенство, сходство, порядок. М.: Наука, 1971. 255 с.
- Мелихов А.Н., Бернштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечеткой логикой. М.: Наука, 1990. 272 с.
SYNTHESIS AND ANALYSIS OF HAZARDS STRUCTURE BASED ON FUZZY BINARY RELATIONS
Palyukh B.V., Dr.Sc. (Engineering), Professor; Semenov N.A., Dr.Sc. (Engineering), Professor;
Bogatikov V.N., Dr.Sc. (Engineering), Professor; Alekseev V.V., Ph.D. (Engineering), Associate Professor; Kemaykin V.K., Ph.D. (Engineering), Associate Professor
(Tver State Technical University, Nikitin Quay 22, Tver, 170026, Russian Federation, is@tstu.tver.ru);
Vent D.P., Dr. Sc. (Engineering), Professor; Prorokov A.E., Ph.D. (Engineering), Associate Professor;
Sanaeva G.N., Senior Lecturer
(Novomoskovsk Institute of MUCTR. D.I. Mendeleev, Druzhby St. 8, Tula Reg., Novomoskovsk,
301665, Russian Federation, k_vtit@dialog.nirhtu.ru);
Toichkin N.A., Ph.D. (Engineering), Associate Professor, toichkin@list.ru
(Kola branch of Petrozavodsk state University, Lesnaya St. 29, Murmansk Reg., Apatity,
184209, Russian Federation)
Abstract. The paper considers the synthesis of structures dangers based on fuzzy binary relations and building on its based the diagnostic algorithm of state control and safety technologies. Methodical principles developed in the work based on the concept of safety center – the region of most safely of functioning of chemical-technological process (CTP). Safety of CTP estimated by the index safety which is defined as the degree of remoteness of the current state of the process, from the safety center and calculated through the degree of inclusion of the current fuzzy situation to the fuzzy situation of the safety center. The method of determining scenarios of hazards on the basis of fuzzy graph of emergency situations are discussed.
Principles of diagnostics, developed in work provide an effective tool for evaluating technological process safety and decision-making, and can be used for building a diagnostic states system and managing of technological process safety.
Keywords: technological safety, safety control, fuzzy binary relations, chemical-technological process, fuzzy graph, diagnostic system of states, safety center, safety degree.
Comments