Современное химическое производство представляет собой сложный комплекс целенаправленно организованных технологических процессов, являющихся источником повышенной опасности для человека и окружающей среды, поэтому вопросу обеспечения технологической безопасности в данной сфере уделяется самое пристальное внимание.

Прежде чем дать определение технологической безопасности, необходимо отметить, что одним из основных свойств множеств опасностей, присущих химико-технологическим процессам (ХТП), является наличие структуры этих множеств, которая возникает как результат упорядочивания опасностей. Поэтому с точки зрения практического применения необходимым этапом исследования технологической
безопасности является теоретико-множественный анализ опасностей, который позволяет их структурировать. Структура опасностей ложится в основу разработок мероприятий для их нейтрализации. От правильности структуры опасности зависит эффективность мероприятий, эффективность управления технологической безопасностью.

Обобщенное понятие технологической безопасности

В данной статье под технологической безопасностью понимается свойство технологической системы (ТС) выполнять свои функции без нанесения ущерба окружающей среде, здоровью работающих в сфере производства людей, оборудованию и системе управления (СУ), регламенту ведения промышленного процесса по технологическим причинам, способным повлечь за собой вышеназванные составляющие ущерба [1].

Технологическая безопасность интерпретируется функциональным свойством соответствующих человеко-машинных систем, в общем случае включающих в себя объект управления, источники опасностей (непосредственно технологический процесс, технологическое оборудование, СУ) и потенциальные жертвы его вредных энергетических и материальных выбросов (обычно людей и окружающую их среду). Множество опасностей порождает множество мероприятий для их нейтрализации.

Понятие технологической безопасности является сложным, качественная и количественная оценки формируются на основе анализа отношения множества опасностей и мероприятий, нейтрализующих эти опасности. Такие источники и мероприятия характеризуют степень защищенности и формируют оценку технологической безопасности работы промышленных процессов.

Продолжая описание понятия безопасности, можно отметить, что как производное от этого понятия возникает понятие риска, которое характеризует возможные последствия от возникновения той или иной нештатной ситуации.

В современной литературе делаются попытки описать безопасность на основе обобщенных технико-экономических функциональных зависимостей. Чаще всего это риск – показатели, которые опираются на вероятностные свойства системы, построенные на основе показателей безотказной работы технологических систем.

Наиболее общее и законченное представление функции заключается в рассмотрении ее как соответствия. В данном случае областью отправления соответствия является множество источников опасностей и защитных мероприятий, областью прибытия – оценка безопасности промышленного объекта.

Основные операции и отношения на множествах, формирующих оценку безопасности

Рассмотрим основные свойства множеств, которые формируют оценку безопасной работы технологических систем. Сводка теоретических результатов теории множеств выполнена на основе первоисточников [2–7].

Будем предполагать, что множества отправления счетные и конечные. Основным множеством, определяющим соответствие, является множество опасностей. Обозначим данное множество через О.

Бинарным отношением R на множестве О называют подмножество R множества О´О, то есть рассматривается множество упорядоченных пар вида <x, y>, называемое декартовым произведением, где x и y – элементы множества О. Таким образом, строго говоря, отношение – это пара <R, О>.

Поскольку операции объединения и пересечения отношений возникли из теоретико-множественных операций объединения и пересечения, все их свойства точно такие же, как и у теоретико-множественных операций.

Рассмотрим некоторые из операций, которые не сводятся непосредственно к теоретико-множествен-ным.

Операция R-1 носит название операции обращения. xR-1y равносильна yRx. У операции R-1 есть важное свойство, оно выражается равенством (R 1)–1=R.

Существенную роль играет операция, обозначаемая R1R2 произведения отношений. Она определяется следующим образом: соотношение xR1R2y равносильно тому, что существует такое z О, для которого выполнены соотношения xR1z и zR2y. В общем случае эта операция не перестановочна; в случае, когда R1R2=R2R1, говорят, что R1 и R2 коммутируют.

Диагональное отношение Е играет роль единицы: ЕR=RЕ=R.

Аналогично для пустого отношения имеем ÆR=RÆ=Æ.

Ассоциативный закон: (R1R2)R3=R1(R2R3).

Первый дистрибутивный закон: (R1ÈR2)R3=(R1ÈR3)(R2ÈR3).

Второй дистрибутивный закон: (R1ÇR2)R3Í(R1R3)Ç(R2R3).

Определим операцию дополнения. Отношение Rд называется дополнением отношения R, если оно выполняется для тех и только для тех пар, для которых не выполняется отношение R. Очевидно, что
Rд =О\R.

На основе операций дополнения и обращения вводится операция перехода от отношения R
к двойственному отношению Rd. Двойственным к R называется отношение Rd, определяемое формулой Rd=(Rд)-1.

Определим еще одну важную операцию, которая называется транзитивным замыканием отношения R и будет обозначаться через R·. Если R – некоторое отношение на множестве О, то его транзитивное замыкание определяется следующим образом. Соотношение xR·y считается выполненным, если существует цепочка элементов из О: z0=x, z1, z1, …, zn=y, такая, что между соседями в этой цепочке выполнено отношение R: z0Rz1, z1Rz2, …, zn-1Rzn. Используя операцию объединения, этот факт можно записать в виде равенства: R·=RÈR2ÈR3È…ÈRnÈ…

Рассмотрение свойств бинарных отношений играет важную практическую роль в упорядочении и классификации опасностей и в дальнейшем в реализации мероприятий по уменьшению опасностей. В зависимости от того, как определяется бинарное отношение, может быть построено различное упорядочение опасностей и, соответственно, различный порядок выбора тех или иных рекомендаций по управлению безопасностью промышленных объектов.

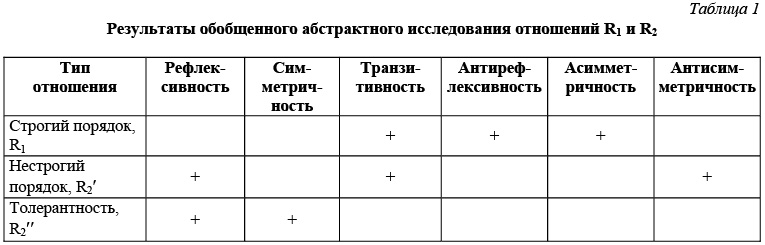
Например, определим отношение R1 как «быть опаснее». В этом случае между элементами множества может быть введен строгий порядок. Если рассматривать отношения R2 как «быть опаснее или эквивалентно», в этом случае может возникнуть или нестрогий порядок, или толерантность (табл. 1).

Доказательство этих утверждений опирается на проверку свойств рефлексивности, транзитивности, антирефлексивности, асимметричности, антисимметричности.

Определение 1. Отношение R называется рефлексивным, если. Иначе говоря, рефлексивное отношение всегда выполнено между объектом и им самим.

Из определения видно, что отношение R1 «быть опаснее» рефлексивным быть не может, так как один и тот же объект не может быть опаснее самого себя.

С другой стороны, отношение R2 допускает эквивалентность и, следовательно, является рефлексивным.

Определение 2. Отношение R называется антирефлексивным, если из xRy следует x¹y, то есть отношение R может выполняться лишь для несовпадающих объектов.

Отношение R1 «быть опаснее» в соответствии с определением выполняется для несовпадающих объектов. Что касается совпадающих объектов, нельзя сказать, который из них опаснее. Следовательно, R1 является антирефлексивным.

Отношение R2 допускает эквивалентность и, следовательно, антирефлексивным быть не может.

Определение 3. Отношение R называется симметричным, если RÍR-1. Если выполнено соотношение xRy, то выполнено и соотношение yRx.

Для отношения R1 «быть опаснее» свойство симметрии не выполняется.

Для отношения R2, допускающего эквивалентность, может присутствовать свойство симметрии. Если выполняется отношение R2 «быть опаснее или эквивалентно» для xR2y и для yR2x, то это возможно и в случае равенства опасностей x=y. Для отношения R2 может выполняться условие симметричности.

Определение 4. Отношение R называется асимметричным, если RÇR-1=Æ. Это означает, что из двух соотношений xRy и для yRx по меньшей мере одно не выполнено.

Для отношения R1 свойство асимметричности выполняется, для R2 не выполняется.

Определение 5. Отношение R называется антисимметричным, если RÇR-1ÍЕ (Е – диагональное отношение).

Для отношения R1 свойство антисимметричности не выполняется, для R2 выполняется.

Определение 6. Отношение R называется транзитивным, если R2ÍR. Раскрывая алгебраическое условие, приходим к следующему: если xRy и yRz, то выполнено и xRz. Отсюда по индукции следует такое свойство: если xRz1, z1Rz2, …, zn-1Ry, то xRy.

Можно показать, что для рефлексивного отношения R транзитивность эквивалентна равенству R2=R.

Свойство транзитивности играет важную роль в исследовании вопросов безопасной организации работы технологических процессов, так как позволяет установить взаимосвязи, существующие между источниками опасностей и их приемниками, и проследить последовательность событий при возникновении тех или иных внештатных ситуаций.

Для рассматриваемых отношений R1 «быть опаснее» и R2 «быть опаснее или эквивалентно» условие транзитивности практически всегда выполняется, за исключением первичных источников, так как одна опасность порождает другие опасности, существующие в природе.

В таблице 1 приведены результаты обобщенного абстрактного исследования отношений R1 и R2, не привязанные к конкретным объектам химической технологии. Ясно, что в конкретных технологических процессах возможно наличие других отношений между опасностями, которые будут порождать уже бинарные отношения с другими свойствами.

Введем в рассмотрение еще одно отношение, которое называется ацикличным.

Определение 7. Отношение R ациклично, если RkÇR-1=Æ для любого k. Ацикличность R означает, что из xRz1, z1Rz2, …, zn-1Ry следует x¹y.

Ацикличность и транзитивность отношений важны в теории выбора и принятия решений, так как эти свойства выражают некоторые взаимосвязи между объектами. Действительно, если х в некотором смысле лучше, чем у, а у в том же смысле лучше, чем z, то естественно считать, что в этом смысле х лучше, чем z (транзитивность), во всяком случае z не лучше х (ацикличность).

Определение 8. Отношение R называется отрицательно транзитивным, если его дополнение Rд транзитивно.

Отношения эквивалентности и толерантности

Из таблицы 1 видно, что отношения R1 «быть опаснее» и R2 «быть опаснее или эквивалентно» порождают комбинации свойств бинарных отношений. Необходимо отметить, что в природе существуют
множества, которые характеризуются различными комбинациями свойств бинарных отношений. Если исходить из количества свойств бинарных отношений (в таблице 1 их шесть), общее количество типов отношений в данном случае равняется 26, или 32. Однако некоторые из них несовместны (например асимметричность и антисимметричность), то есть, если элементы отношения обладают свойством асимметричности, то свойством антисимметричности они обладать уже не могут.

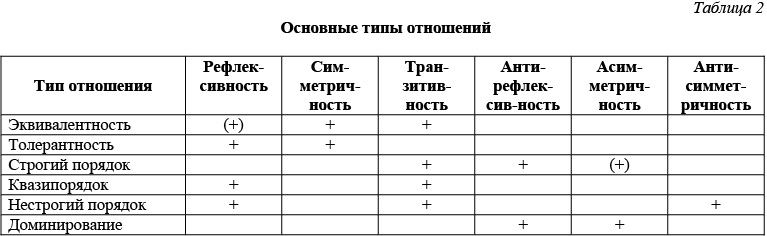
Таким образом, свойства множеств можно определить на основе бинарных отношений между элементами множеств. Список основных типов отношений, представляющих наибольший практический интерес, приведен в таблице 2. Знак (+) показывает, что данное свойство вытекает из всех остальных.

На основе анализа типов отношений можно получать разбиения множества опасностей.

Определение 9. Систему непустых подмножеств {О1, О2, …} называют разбиением этого множества, если О=О1ÈО2È… и О1ÇО2Ç…=Æ при i¹j. Сами множества О1, О2, … называют при этом классами данного разбиения.

Определение 10. Отношение R на множестве называется эквивалентностью (или отношением эквивалентности), если оно рефлексивно, симметрично и транзитивно.

Теорема 1. Если отношение R на множестве О рефлексивно, симметрично и транзитивно, то существует такое разбиение {О1, О2, …} множества О, что соотношение xRy выполнено в тех случаях, когда x и y принадлежат общему классу разбиения.

Иначе, если задано разбиение {О1, О2, …} множества О и бинарное отношение R определено как «принадлежать общему классу разбиения», то R рефлексивно, симметрично и транзитивно.

Таким образом, отношение R на множестве О называется эквивалентностью (или отношением эквивалентности), если существует такое разбиение {О1, О2, …} множества О, что соотношение xRy выполняется тогда и только тогда, когда x и y принадлежат одному классу Оi данного разбиения.

Возникает вопрос, не являются ли некоторые аксиоматические свойства эквивалентности излишними. Можно доказать следующее утверждение: если отношение R симметрично и транзитивно, то оно и рефлексивно (эквивалентность). Возьмем произвольный элемент x и такое y, что выполнено соотношение xRy. Тогда в силу симметричности верно и соотношение yRx. В силу транзитивности отсюда следует xRx.

Определение 11. Отношение R на множестве О называется толерантностью (или отношением толерантности), если оно рефлексивно и симметрично.

Толерантность присуща технологическим объектам. Она характеризует возникновение локальных очагов опасностей, но не предполагает связи между опасностями.

Рассмотрим на примере типовой системы автоматического регулирования (САР) порождение различных типов отношений в зависимости от определения бинарного отношения (рис. 1). В нижеприведенных примерах будем полагать, что объект работает исправно.

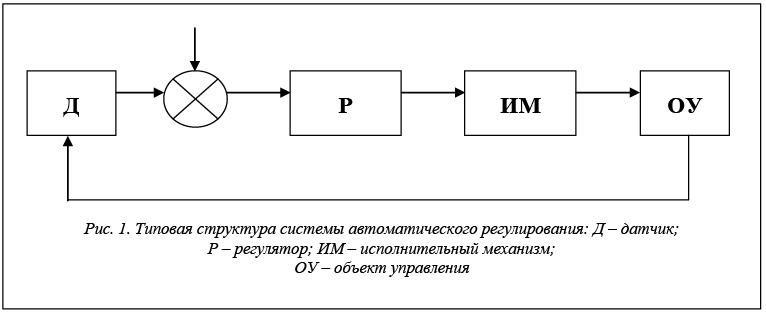
В первом примере определим отношение R –  «порождает». Допустим, что каждый элемент САР (датчик, регулятор и исполнительный механизм) работает автономно. В принципе так оно и есть, если не рассматривать влияние результатов работы каждого из них на результаты совместной работы, а регистрировать неисправности только конкретных элементов системы. Возникает вопрос о правомерности применения такого бинарного отношения. Поясним смысл анализа этого отношения, который базируется на идеализации ситуации и основное назначение которого – проиллюстрировать, к какому результату приведет применение данного бинарного отношения. Конечно, рассматривать работу каждого элемента САР независимо от других нельзя. Но, с другой стороны, этот анализ позволяет показать характерную особенность свойства толерантности – отсутствие транзитивности или взаимосвязи между источниками опасностей.

В случае сознательного огрубления свойств объекта такое предположение оправдано.

Множество опасностей можно определить следующим образом (предположим, для данного случая): О={xд, xр, xим}, где xд – неисправность датчика; xр – неисправность регулятора; xим – неисправность исполнительного механизма.

Далее приведем матрицу отношения R на множестве О (табл. 3).

В этом случае отношение R обладает свойством рефлексивности и симметричности. Этот факт вытекает из следующих простых рассуждений: неисправность или датчика, или регулятора, или исполнительного механизма не порождает неисправностей других элементов системы. С другой стороны, видно, что матрица диагональная, следовательно, бинарное отношение симметричное и данное отношение является толерантностью.

Во втором примере рассмотрим отношение R «порождает неправильную работу». Под неправильной работой будем понимать нарушения в работе САР. В этом случае предполагается зависимость результатов работы отдельных звеньев САР от результатов работы системы в целом. Это отношение уже отражает взаимосвязи, существующие в системе.

Анализ данного отношения показывает следующее: неисправность датчика xд «порождает неправильную работу» регулятора xр и исполнительного механизма xим, то есть отношения xдRxр и xдRxим выполняются; неисправность регулятора xр «порождает неправильную работу» исполнительного механизма xим и неправильную работу датчика xд, то есть отношения xдRxр и xдRxим выполняются; аналогичная ситуация возникает и в случае неисправности исполнительного механизма xим. Неисправность исполнительного механизма xим «порождает неправильную работу» регулятора xр и датчика xд.

Если не рассматривать совместных появлений событий неисправности элементов системы, матрица отношения R на множестве О для данного примера запишется, как в таблице 4.

Таким образом, возникает отношение, которое характеризуется рефлексивностью, симметричностью и транзитивностью, то есть эквивалентность.

Отрицательным свойством эквивалентности в данном случае является то, что при появлении какого бы то ни было нарушения в работе САР нельзя сказать, какой элемент системы неисправен. Возникает неопределенность в нахождении первичного источника нарушения, что является задачей диагностики того или иного нарушения.

В вышеприведенном примере количество последовательностей поиска неисправностей не так велико. Их всего шесть. Это легко проверить простым перечислением вариантов поиска. Например: 1) Р, ИМ, Д; 2) Р, Д, ИМ и т.д. Если обобщать результат, то число вариантов поиска будет равно n!, где n – число элементов системы.

Проблема поиска – основная проблема задач диагностики, задач, так или иначе связанных с обнаружением неисправностей в технологических системах, с необходимостью раскрытия неопределенности.

В то же время существование связи между опасностями является важным свойством промышленных объектов с точки зрения развития критических и аварийных ситуаций, когда одна опасность порождает другие источники опасностей. Порождение опасностей может развиваться как цепная реакция.

Особую роль эти связи начинают играть в решении задач диагностики состояний и в управлении безопасностью при анализе порядка следования событий, происходящих при зарождении одной опасности и появлении следующих опасностей, взаимосвязанных с первичным источником. В этом случае необходимо решать задачу раскрытия неопределенности при определении первоисточника возникновения опасного нарушения.

Отношения порядка

Определение 12. Отношение R на множестве О называется отношением строгого порядка (или строгим порядком), если оно антирефлексивно и транзитивно.

Таким образом, отношение строгого порядка на множестве О обладает следующими свойствами: ни для какого xÎО не выполнено xRx; если xRy и yRz, то выполнено xRz; если выполнено xRy, то yRx невозможно. Первые два условия образуют определение строгого порядка, а третье из него следует.

Множество с заданным на нем отношением строгого порядка называют упорядоченным множеством.

Определение 13. Отношение строгого порядка R называют совершенно строгим порядком, если для всякой пары несовпадающих элементов <x, y> из О верно либо xRy, либо yRx.

Если на множестве О задано отношение совершенно строгого порядка R, то на множестве О2 всех пар возникает разбиение на три класса: класс пар вида <x, x>, класс пар <x, y>, таких, что xRy, и класс пар
<y, x>, таких, что yRx.

Определение 14. Пусть на множестве О задано отношение строгого порядка <. Тогда элемент xÎО называется минимальным (максимальным) в упорядоченном множестве <О, <>, если не существует никакого элемента y, для которого y<x (соответственно y>x).

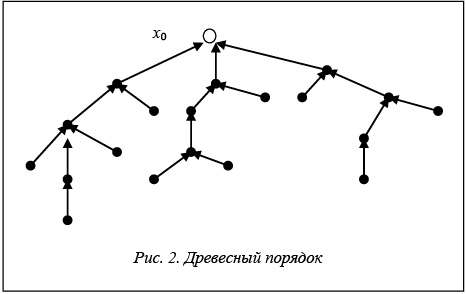
В случае совершенно строгого порядка минимальный элемент x обладает тем дополнительным свойством, что для всякого y¹x выполнено x<y. В общем случае может оказаться так, что элемент x минимален, но не находится в соотношении x<y с какими-то иными элементами. Примером этому может быть древовидный порядок (дерево отказов, дерево событий). Элементы x и y должны быть сравнимы. Элементы x и y называются сравнимыми в данном упорядоченном множестве <О, <>, если x<y, или x=y, или y<x.

Определение 15. Отношение R на множестве О называется отношением нестрогого порядка (или нестрогим порядком), если оно может быть представлено в виде R=R1ÈE, где R1 – строгий порядок на О, а E – диагональное отношение.

Любое отношение нестрогого порядка рефлексивно, антисимметрично и транзитивно. Нестрогий порядок R называют совершенным, если для любой пары x, y верно либо xRy, либо yRx. Из антисимметричности нестрогого порядка следует, что одновременное выполнение xRy и yRx означает x=y.

Из определения нестрогого порядка следует: если R – совершенный нестрогий порядок, то R1=R\E есть совершенный строгий порядок. Если же R1 – совершенный строгий порядок, то R=R1ÈE есть совершенный нестрогий порядок.

Рассмотрим еще одну операцию, которая носит название редукции.

Определение 16. Редукцией отношения R называется отношение Rr, определяемое условием Rr=R\R2.

Это означает, что если xRry выполняется в тех случаях, когда выполнено отношение xRy, то не существует промежуточного z, такого, что xRz и zRy. Отношение xRry означает непосредственное подчинение элемента x элементу y.

В практических исследованиях множеств опасностей с точки зрения управления технологической безопасностью важную роль играет специальный класс отношений, так называемые древесные порядки.

Пусть имеется множество О с отношением строгого порядка <. Элемент x0 называют наибольшим, если для всякого элемента yÎО, отличного от x0, выполнено соотношение y<x0. Легко видеть, что наибольший элемент (если он существует) единственен.

Определение 17. Отношение строгого порядка < на множестве О называется отношением древесного порядка (или древесным порядком), если

из x<y и x<z следует, что y и z сравнимы;

во множестве <О, <> существует наибольший элемент.

Множество О с заданным на нем древесным порядком, то есть пару <О, <>, называют деревом, а наибольший элемент – корнем дерева.

Первое условие означает, что для любого элемента xÎО на множестве элементов, больших, чем x, исходный древесный порядок превращается в совершенный порядок. Нетрудно видеть, что совершенный порядок, в котором существует наибольший элемент, есть частный случай древесного.

Рассмотрим некоторые свойства древесного порядка.

Лемма 1. Если R – древесный порядок на О, то на множестве О(x), состоящем из самого x и элементов yÎО, таких, что yRx, отношение R также задает древесный порядок.

Множество О(x) с порядком R называют поддеревом дерева <О, R>.

Лемма 2. Если R – древесный порядок на О, то для всякого x, отличного от корня x0, существует ровно один y, для которого выполнено xRry.

Лемма 3. Пусть < древесный порядок на конечном множестве О. Тогда для любых несравнимых элементов xÎО и yÎО существует единственный элемент zÎО, для которого x<z, y<z, и если x<w и y<w, то z<w.

С помощью приведенных выше лемм можно убедиться, что граф, изображающий редукцию Rr древесного порядка R на конечном множестве О, имеет древовидную структуру. Окрестностью элемента y называют совокупность элементов z, для которых выполнено xRry. Будем изображать граф Rr по ярусам (рис. 2). В первом ярусе поместим корень дерева – наибольший элемент х0; во втором – элементы, входящие в окрестность элемента х0; в третьем – входящие в окрестность элементов второго яруса и т.д. Стрелки в графе могут идти только от яруса к ярусу. При этом от каждого элемента к верхнему ярусу идет ровно одно ребро, а к нижнему – сколько угодно. Граф имеет структуру дерева. Общее число ярусов называется высотой дерева. Максимальное число элементов в одной окрестности (максимальное число ростков, выходящих из одной вершины) называется шириной дерева.

Высота дерева h, ширина дерева d и общее число вершин n связаны неравенством n£1+d+d2+…+dh-1=(dh–1)/
(d–1), которое обращается в равенство в том случае, когда окрестность каждого элемента (кроме элементов самого нижнего яруса) состоит из d элементов.

Сложность конечного дерева можно характеризовать следующим рекуррентным правилом: g(x)=d(x)+g(y), где y – единственный элемент, для которого xRry. Иначе говоря, сложность вершины x складывается из количества ростков, выходящих вниз из этой вершины, и сложности вершины предыдущего яруса, соединенной с x. При x=x0 принимают g(y)=0.

Сложность дерева g(D) определяется как суммарная сложность его вершин:

g(D)=Sg(x), xÎО.                                (1)

Из равенства (1) легко получить g(x)=d(x)+Sd(y), x<y.

Подставляя это выражение для g(x), получим

g(x)=Sd(y)k(y), yÎО,                           (2)

где через k(y) обозначено, сколько раз величина d(y) участвует в выражении для g(D).

Данные соотношения могут оказаться полезными при оценке уровня опасностей для различных технологических процессов.

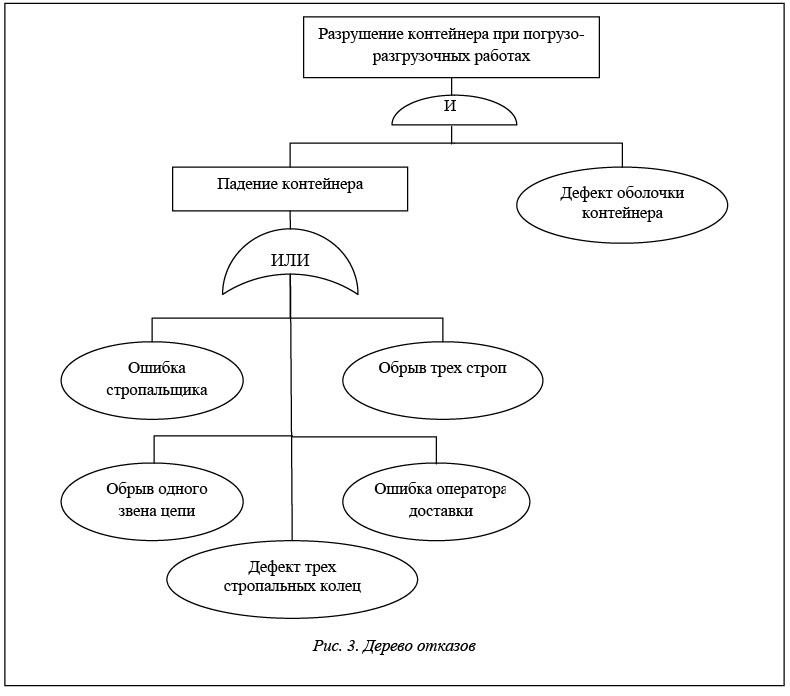
Иллюстрацией возникновения древесного порядка на основе отношения R «порождает отказ» может быть результат анализа опасностей погрузо-разгрузочных работ, например, контейнера хлора на складе хлора, который определяет источники опасностей и возможные последствия отказов (рис. 3).

На основе подобного анализа в практических исследованиях осуществляется построение деревьев отказов, которые в дальнейшем используются в создании сценариев развития аварий, различного рода нештатных ситуаций, в управлении технологической безопасностью.

Определение 18. Отношением доминирования называется отношение, обладающее свойствами антирефлексивности и асимметричности. Говорят, что х доминирует у, и пишут х>>у, если х в каком-либо смысле превосходит у. Можно отметить, что отношение строгого порядка является частным случаем отношения доминирования.

Одним из основных свойств множеств опасностей, присущих технологической системе, является наличие структуры этих множеств, которая возникает как результат упорядочивания опасностей. Поэтому на практике необходимым этапом исследования является теоретико-множественный анализ опасностей, который позволяет структурировать опасности. Структура опасностей ложится в основу разработок мероприятий для их нейтрализации. От правильности структуры опасности зависит эффективность мероприятий и управления технологической безопасностью.

Теоретико-множественные свойства управляющих воздействий по обеспечению технологической безопасности

Выше были рассмотрены свойства множеств опасностей. Отмечено, что в исследовании технологической безопасности определяющую роль играют множества опасностей. Мероприятия по обеспечению технологической безопасности как множества (их можно также называть управляющими воздействиями) обладают некоторыми отличительными особенностями.

С одной стороны, они формируются в прямой зависимости от конкретных опасностей, с другой, отдельные мероприятия по обеспечению технологической безопасности вносят свой вклад в обеспечение безопасности и от других опасностей (обеспечивают безопасность с меньшим эффектом для данной опасности) и тем самым влияют на технологическую безопасность всего технологического процесса.

Конечно, как множества они могут быть подвергнуты операциям пересечения, объединения и т.д., могут обладать свойствами рефлексивности, транзитивности и т.д.

Свойства эквивалентности и упорядочения возникают при совместном анализе конкретной опасности и мероприятий, нейтрализующих эту опасность. Критерием выбора того или иного управления (мероприятия) служит уровень безопасности, который он обеспечивает.

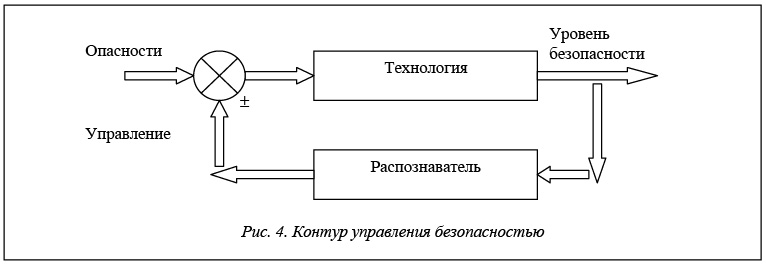
Приведенные рассуждения иллюстрируются на рисунке 4. Рассматривать теоретико-множественные операции целесообразно для тех из них, которые предназначены для нейтрализации одной или нескольких опасностей. В этих условиях имеют смысл операции объединения, пересечения и т.д.

Особый интерес представляет отношение R «связаны» на декартовом произведении О´U (U – множество мероприятий). Связность понимается по целевому назначению мероприятий, то есть по опасности, которую они нейтрализуют.

В этом случае возможны пересечения множества ÇU(хi), хi ÎО. Это свойство пересечений можно использовать в классификации и упорядочении мероприятий, а также в оценке уровня безопасности технологического процесса.

Концептуальная модель технологической безопасности

Наиболее общее формальное описание технологической безопасности можно задать в следующем виде: объект «технологическая безопасность» Тб определяется кортежем

Тб=<О, U, А, R(О, U), В(О, U)>,                      (3)

где О – множество опасностей; U – множество мероприятий, нейтрализующих опасности (управлений); А – семейство алгебраических операций; В(О, U) – множество оценок уровня безопасности, которые являются отображением соответствия R(О, U) (отношения), построенного на декартовом произведении О´U, на нормированное по некоторому правилу множество реальных чисел (например, это может быть интервалом [0,1]) либо на булевское множество <false, true>. В последние годы развивается подход, основанный на интервальных оценках неопределенности.

Таким образом, можно записать, что существует отображение f: R(О, U)®В или в=f(x, u), где xÎO, uÎU, вÎВ. Причем для реальных объектов допустимо предположение, что множества О и U либо конечные, либо счетные.

Отображение f в том виде, в котором оно записано, имеет следующие особенности:

– значения функции вÎВ зависят от двух переменных xÎO и uÎU, нельзя сказать с полной определенностью, что выполняются условия биекции;

– условия инъекции, скорее всего, не выполняются, так как область определения задается перечислением множеств О и U, а значения функции из множества В для различных элементов множества R(О, U) могут совпадать;

– наиболее вероятно, что отображение f будет сюръективным;

– определение множества В осуществляется на основе экспертных процедур, так как измерить уровень безопасности в настоящее время не представляется возможным;

– для булевского множества значений В о безопасности судят по исправности устройства управления, аппарата, технологического процесса. Считается, что технологическая система удовлетворяет некоторому уровню безопасности, если все исправно, нет сбоев в оборудовании, СУ, нет технологических сбоев. При таком подходе к определению множества В отображение f: R(О, U)®В будет биективным.

Приведенные выше рассуждения не являются доказательством свойств отображения f, так как необходимо знать в=f(x, u). Это аксиоматические предположения, а не аксиомы выбора вида f(x, u).

Такой анализ отображения f: R(О, U)®В допустим при наличии достаточного количества информации о состоянии технологического процесса, то есть о состоянии оборудования, СУ. Однако системы безопасности современных химических производств являются сложными организационно-технологическими системами, обладающими следующими основными свойствами:

– разнородность, неопределенность, содержательный характер информации;

– нечеткий характер технологических процессов;

– широкий спектр различных возмущающих и управляющих воздействий;

– сложный характер их влияния;

– сложность в различимости первопричин возникновения тех или иных нарушений.

Зачастую либо процессы управления организационно-технологических систем плохо формализуемы, либо невозможно создать математическую модель. Примером плохо формализуемого объекта является организационно-технологическая система управления технологической безопасностью.

Как следствие, такие свойства системы безопасности порождают характерную особенность множества опасностей – стохастический, нечеткий характер проявления опасностей, который выражается в случайном возникновении различного рода нештатных ситуаций при эксплуатации технологических процессов. Дело в том, что само множество опасностей постоянно присутствует при эксплуатации технологического процесса. Проявление же опасностей носит случайный характер.

Это свойство усложняет вид и анализ отображения f: R(О, U)®В. Кроме того, усложняется и анализ множества опасностей О. Как следствие этих причин возникает необходимость в исследовании статистических закономерностей проявления опасностей.

Однако теоретико-множественный анализ необходим для классификации опасностей, установления порядка и синтеза структуры возникновения опасностей, анализа развития событийных процессов при появлении какой-либо опасности, синтеза управляющих воздействий (это организационно-технологические мероприятия), выбора оценки уровня безопасности (выбор вида отображения f:
R(О, U)®В).

Таким образом, на начальном этапе исследования технологической безопасности выполняется перечисление множеств О и U. На основе бинарных отношений определяются свойства множеств, осуществляются их классификация и упорядочение, задание структуры опасностей.

На следующем этапе для целей управления исследуется событийный характер проявления опасностей. Отсутствие статистически полноценной информации накладывает ограничения на применение различных разделов математики, связанных со статистическими исследованиями. В настоящее время наиболее часто применяется математический аппарат нечетких множеств.

Надо отметить, что при исследовании технологической безопасности аппарат теории вероятностей и математической статистики не исключается при рассмотрении различного рода отказов, связанных с протеканием химико-технологического процесса (технологические нарушения). При анализе опасностей, связанных со сбоями оборудования и систем управления, статистический материал часто либо отсутствует, либо его недостаточно.

Литература

1. Богатиков В.Н. Диагностика состояний и управление технологической безопасностью непрерывных химико-технологических процессов на основе дискретных моделей: дис. … докт. техн. наук (05.13.06). Апатиты, 2002. 337 с.
2. Общая алгебра; [под общ. ред. Л.А. Скорнякова]. М.: Наука, 1990. Т. 1. 592 с.
3. Общая алгебра; [под общ. ред. Л. А. Скорнякова]. М.: Наука, 1991. Т. 2. 480 с.
4. Макаров И.М., Виноградская Т.М., Рубчинский А.А., Соколов В.Б. Теория выбора и принятия решений: учеб. пособие. М.: Наука, 1982. 328 с.
5. Трухаев Р.И. Модели принятия решений в условиях неопределенности. М.: Наука, 1981. 258 с.
6. Кафаров В.В., Дорохов И.Н. Системный анализ процессов химической технологии. Основы стратегии. М.: Наука, 1976. 500 с.
7. Шрейдер Ю.А. Равенство, сходство, порядок. М.: Наука, 1971. 255 с.

 

ON THE APPLICATION OF THE SET-THEORETIC APPROACH TO THE TECHNOLOGICAL SECURITY DEFINITION

 

Vent D.P., Dr. Sc. (Engineering), Professor; Prorokov A.E., Ph.D. (Engineering), Associate Professor; Sanaeva G.N., Senior Lecturer

(Novomoskovsk Institute of MUCTR. D.I. Mendeleev, Druzhby st. 8, Tula Reg., Novomoskovsk, 301665,
Russian Federation, k_vtit@dialog.nirhtu.ru);

Toichkin N.A., Ph.D. (Engineering), Associate Professor, toichkin@list.ru

(Kola branch of Petrozavodsk state University, Lesnaya st. 29, Murmansk Reg., Apatity, 184209,
Russian Federation);

Palyukh B.V., Dr.Sc. (Engineering), Professor; Semenov N.A., Dr.Sc. (Engineering), Professor;
Bogatikov V.N., Dr.Sc. (Engineering), Professor; Alekseev V.V., Ph.D.  (Engineering), Associate Professor; Kemaykin V.K., Ph.D. (Engineering), Associate Professor

(Tver State Technical University, Nikitin Quay 22, Tver, 170026, Russian Federation, is@tstu.tver.ru)

 

Abstract. The paper focuses on the definition of the technological security set-theoretic point of view. Concept of technological safety as the functional properties of the system are discussed.

The necessity of the use of set-theoretic approach to the study of the properties of technological security on the basis of binary relations. An overview of the basic operations and relations on the sets forming the safety assessment.

It is shown that from the point of view of practical application in the analysis of technological safety, a necessary stage in the research is the set-theoretic analysis of the dangers that allows you to structure risk. The revealed structures of dangers can be laid the foundation for the activities developed for the diagnosis purpose and management of emergency situations of technological safety of the studied object.

As the result the conclusion about the need to investigate the nature of the dangers of casual event for the management of technological security, what actually apply the mathematical apparatus of fuzzy sets.

Keywords: technological safety, chemical-technological process, set-theoretic approach, binary relations, security management.