There are thousands of NP-complete tasks in various fields, such as cartography, x-ray crystallography, cryptography, and training of intelligent agents [1].
This class contains a significant portion of fundamental problems whose complexity cannot be resolved since it is known that the NP-complete problem cannot yet be solved in polynomial time.
Currently, the evidence that the problem being solved is NP-complete is the reason for stopping the search for an effective algorithm for this problem [2].
S. Cook laid the Foundation for the theory of NP-complete problems in 1971. [3] proves that any NP-complete problem can be reduced to any other NP-complete problem in polynomial time, thus proving the NP-completeness of many known combinatorial problems [4].
The implication is that by solving one problem, you can get solutions to other NP-complete problems using reduction algorithms.
As a result, the solution is simplified since for some problems heuristic algorithms are found that obtain a solution close to optimal. However, it is not the case. In most cases, existing reduction algorithms only prove NP-completeness but do not help to find solutions through other problems [5]. Creating exactly such reduction algorithms for NP-complete problems is an urgent problem.
The goal of this paper is the design of the algorithm reduction of a binary cooperative assignment problem (2-AP) to a travelling salesman problem (TSP) for solving determination.
Reducing NP-Complete Problems
To prove the NP-completeness of a certain problem A, it is sufficient to show that a certain known
NP-complete problem B can be reduced to A. For information, there are three general methods: restriction
of a problem, local replacement, and component construction [6].
The simplest and most frequently used method for proving NP-completeness is the restriction of a problem. The idea is to find out the additional restrictions that need to be imposed on problem B so that the resulting problem is equivalent to A. In other words, we need to show that A includes a special case of problem B.
A striking example of this method is the reduction of the traveling salesman problem to the problem of the Hamiltonian cycle and back.
The traveling salesman problem [7; 8] is to find the shortest Hamiltonian cycle in a weighted oriented graph. The problem of a Hamiltonian loop is finding a loop that visits every node of the graph.
From a mathematical point of view, the salesman's problem can be described as follows.
There are n cities. Each city is characterized by the following values:
xij – the i city path out an existence to the j city:
xij=1, if the path exists and xij=0 if otherwise;
cij − the path cost from i city i to j city, cij≥0.
The traveling salesman problem is to find the minimum path that passes through these cities at least onceand then return to the base city.
The TSP problem’s representation as a graph has the following form.
The directed graph G = (V, E) is TSP instance, if |V|=n, and eij=cij, if xij = 1, i, j ∈ V. The problem is to find the minimum weight Hamiltonian cycle.
The reduction of the Hamiltonian cycle problem to the traveling salesman problem is obvious [5] since
the Hamiltonian cycle problem is a special case of the traveling salesman problem.
The P-code:
numberVertices = getNumberVertices (Hamilton Graph)
tspGraph = createCompleteGraph(numberVertices)
foreach edge in tspGraph do
if containsEdge (edge, hamiltonGraph)
then setEdgeWeight (edge, 1)
else setEdgeWeight (edge, numberVertices + 1)
end if
end foreach
return (G, numberVertices)
As you can see from the P-code, all infinite paths are replaced with weight paths. It follows that if the original Hamiltonian cycle did not exist, this algorithm will still give a positive answer since the minimum path will be found. Introducing an extra condition that the shortest path should not exceed the number of vertexes corrects this error, but in more complex cases, this error can’t be eliminated.
It should be noted that not all graph problems are NP-complex, depending on the conditions; they can
be solved in polynomial time [9].
In the reverse reduction, when all weights are replaced by 1, it is obvious that the minimum path will not be found, since there can be many Hamiltonian cycles. And this error can’t be eliminated.
The main problem of the restriction method is that the problem arising as a result of the restriction does not have to be an exact copy of the known NP-complete problem, only a one-to-one correspondence between the problems is necessary, preserving the answers "yes" and "no".
The local replacement method consists in choosing some characteristic property of a known NP-complete problem, using it to form a family of basic modules, and obtaining the corresponding individual problems of a given problem by uniformly replacing each basic module with some other structure.
When replacing, some boundary cases of the given problem are often omitted, so this method is not suitable for the exact solution of the given problem through reductions.
And the third method is building components. The main idea of such reductions is to construct certain components with the help of the constituent parts of the problem under consideration, connecting which one can realize the individual problems of the known NP-complete problem.
Such method is used in [10] to reduse a vertex cover problem to the problem of finding a Hamiltonian cycle. The vertex coverage problem is to find vertex coverage in the graph with the number of K vertices. In this reduction, for each graph edge, a certain kind of constituents are created that are connected to other constituents and vertices that are responsible for the number of vertices in the vertex coverage. The resulting graph is searched for a Hamiltonian cycle. If the Hamiltonian cycle is found, then the vertex cover exists, and the exact solution is found. But the point is that not always in the absence of a Hamiltonian cycle, there is no vertex cover.
When constructing the constituents, as under a substitution, some situations of the original problem are not considered, so this method is also not suitable for a reduction.
All three methods are not suitable for getting a solution to the original problem via reduction algorithms, since their goal is to prove NP-completeness, and not to solve one problem through another.
Reduce the 2-AP (NP-completeness of which is proved [11]) to the TSP so that the accuracy of the solution of the original problem is preserved.
2-AP definition
The definition of this problem is as follows [11].
There is an upper-level customer who can offer n types of work. m performers who are the lower level perform these problems. The following values characterize the customer:
xi − value of the customer's choice: xi = 1 when ordering work of type i, and xi = 0 if otherwise;
cij − the customer's costs for performing type i of work by j performer (i ∈ I, j ∈ J, |I| = n, |J| = m).
Vector x has length n and consists of zeros and ones − the customer can order any set of works or refuse to perform all the works. Пусть I(x)={i ∈ I, xi = 1} − be the set of ordered works in the variant of choice х. But it is more profitable for the customer to order a maximum of works that can be performed simultaneously: |I(x)| = m.
The following parameters characterize performers:
yij – parameter for selecting performers: уij = 1 when j performer performs the work of i type, and уij=0 if otherwise;
dij – j performer's income
from doing i work (i ∈ I, j ∈ J).
Each performer can choose only one type of work I (x) offered by the customer, and only one performer can perform one type of work.
The lower level problem is to assign work in such a way as to maximize the total income of the performers. The upper-level problem is to minimize the customer's costs, taking into account the decision of the contractors on the choice of work.
Consider setting 2-AP.
Let I = {1, ..., n}, J = {1, ..., m}, x = (x1, ..., xn), y = (yij)i ∈ I, j ∈ J.
Let there be two real matrices С = (cij)i ∈ I, j ∈ J и D = (dij)i ∈ I, j ∈ J. We consider that n ≥ m.
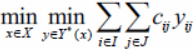 (1)
(1)
where X = {x|xi ∈ {0, 1} (i ∈ I), sumi∈I(xi) = m}, a Y*(x) − set of optimal solutions to the problem
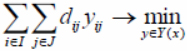 (2)
(2)
Here Y = {y|yij ∈ {0, 1}, sum i∈I(yij) = 1, sum j ∈ J(yij) = xi (i ∈ I, j ∈ J)}
Problem (1) is an upper – level problem, and (2) is a lower-level problem. The lower level is a classic
assignment problem. The upper level counts on the best choice of the lower level.
Reduction algorithm
We present a cooperative two-level assignment problem to the traveling salesman problem. For this, we introduce the following notation:
n (xi = 1) − works ordered by performers, the number of which is equal to m − number of performers.
V − instance graph vertices TSP G = (V, E), the number of which is m+n (xi = 1).
Е − instance graph edges TSP G = (V, E), in the initial notation is the empty set.
The algorithm implementing the reduction of the cooperative 2-AP to the TSP consists of a sequence of the following steps.
Step 1. Construct the graph G = (V, E).
Step 2. Add edges to the set E going from vertices m to each vertex n (xi = 1), with weight dij – 0.1 / cij.
Step 3. Construct edges from vertices n (xi = 1) to each vertex m with weight 0.
Steps 2 and 3 are performed until we have traversed all vertices m and n (xi = 1).
Here is the P-code.
PurposeTSPGraph = createVertices (n (xi = 1) + m)
foreach Vertices_m in PurposeTSPGraph do
foreach Vertices_n in PurposeTSPGraph do
addEdgeWeight (edge, сnm-1/(10*dnm))
end foreach
end foreach
foreach Vertices_n in PurposeTSPGraph do
foreach Vertices_m in PurposeTSPGraph do
addEdgeWeight (edge, 0)
end foreach
end foreach
return (G, numberVertices)
Let us investigate the reduction algorithm to preserve the accuracy of the solution and determine its complexity.
Statement 1. If c, d ∈ N, then the reduction algorithm preserves the accuracy of solving the bilevel problem.
Evidence.
1) The algorithm creates paths in the graph only between customers and performers. The traveling salesman problem is to walk through all the vertices of the graph exactly once, therefore, each performer will receive
exactly one problem.
2) The traveling salesman problem finds the minimum path:
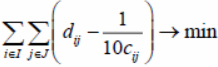 (3)
(3)
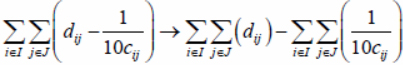 (4)
(4)
To get the minimum value in (3), the first sum in (4) must be minimum and the second maximum.
For the second amount to be maximum, the divisor must be minimum. From this, it follows that what is sought
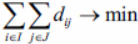 (5)
(5)
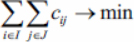 (6)
(6)
From point 1 it follows that formulas (5), (6) can be reduced to the form
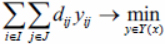 (7)
(7)
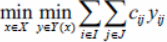 (8)
(8)
3) Since c, d ∈ N, then dij >> 0.1 / cij. It follows from this that the first sum in (4) will be more significant
in the final value than the second sum. This satisfies the condition of the cooperative 2-AP that the upper level counts on the best choice of the lower level. It follows from this that formulas (7) and (8) are transformed into formulas (1) and (2).
This completes the proof. Statement 2. The complexity of the reduction algorithm is quadratic.
Evidence.
The algorithm uses a double loop over m and n = 1 twice. It follows from this that [12]:
О(n*m) + O(m*n) = 2O(n*m) = O(n*m).
From the condition that n = m it follows that
O(n*m) = O(m2).
This completes the proof.
Software implementation.
In the Java programming language, a program was developed that implements the exact solutions of 2-AP and TSP, as well as an algorithm for reducing one problem to another (github.com/ShevelevaAnna/
NP_Complate), the program was tested in accordance with [13].
The exact solution to the traveling salesman problem implements the package of classes package npComplateTSP. class ExactSolutionTSP – the class in this package that is responsible for finding the shortest path. In this class, first the upper bound of the solution is found by the greedy algorithm, then the optimal solution is found by the method of branches and bounds.
The package npComplateCAP class package is responsible for initializing the 2-AP problem, its exact solution, and bringing it to the traveling salesman problem. The class CAP is responsible for generating test problems randomly. Class Reduction2CAPToTSP is responsible for reducing 2-AP to TSP. The class ExactSolution2CAP package finds a set of data with the maximum profit for performers and the minimum loss for the customer by searching through all solutions.
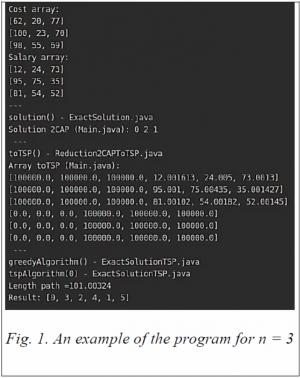
An example of the operation of this program is shown in the figure. 1
This figure shows that the result of the reduction algorithm is correct. The exact solution of 2-AP turned out to be 0-> 0, 2-> 1, 1-> 2. The exact solution of the TSP is 0-> 3, 2-> 4, 1-> 5 or, after transformation, 0-> 0, 2-> 1, 1-> 2.
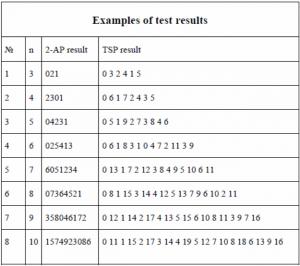
The program was tested for correctness for matrices of dimension n=3 ... n=10 with natural values generated randomly. 100 different tests were created for each n. All tests showed that the 2-AP solutions directly and via the TSP coincide, which means that the reduction algorithm doesn’t affect the accuracy of the problem solution. The table shows examples of test results.
Solution capability for an NP-complete problem in polynomial time
Currently, proving the possibility of solving NP-complete problems in polynomial time or refuting it is one of the seven problems of the millennium. For its solution, the Clay Mathematical Institute awarded a prize of one million US dollars [14].
If a polynomial solution is found for at least one NP-complete problem, then it will automatically be assumed that there is also a polynomial solution for other NP-complete problems. In particular, the encryption algorithms used in asymmetric key cryptography will immediately become defenseless against hacking.
Conclusion
The paper analyzes the existing methods for reducing some NP-complete problems to others. All methods were aimed at proving NP-completeness, and not at getting a solution to one NP-complete problem through another. It followed from this that the existing reduction algorithms do not simplify the computation of NP-complete problems. It was decided to create an algorithm for bringing 2- AP to the TSP to find a solution to the original problem.
The developed reduction algorithm has mathematical studies on the accuracy of getting the solution of the original NP-complete problem and on the computational complexity. The study outcome showed that this algorithm does not affect the accuracy of the 2-AP solution and that the algorithm has quadratic complexity.
The reduction algorithm was also implemented programmatically and tested for correctness. The test results confirmed the mathematical study.
In the future, it is planned to extend the described approach to other NP-complete problems and create a single program for bringing some NP-complete problems to others.
References
- Korobov D.A., Belyaev S.A. Modern Approaches to Training Intelligent Agents in the Atari Environment. Software & Systems, 2018, vol. 31, no. 2, pp. 284–290. DOI: 10.15827/0236-235X.122.284-29 (in Russ.).
- Kleinberg J., Tardos E. Algorithm Design. UK, Pearson Publ., 2005, 864 p. (Rus ed.: St. Petersburg, 2016, 800 p.).
- Cook S.A. The complexity of theorem-proving procedures. Proc. 3rd Ann. ACM STOC, Ohio, 1971, рр. 151–158 (Rus ed.: Moscow, 1975, рр. 5–15).
- Ruiz-Vanoye J.A., Pérez-Ortega J., Pazos R.A., Díaz-Parra O., Frausto-Solís J., Fraire Huacuja H.J., Cruz-Reyes L. Survey of polynomial transformations between NP-complete problems. J. of Computational and Applied Mathematics. 2011, vol. 235, iss. 16, pp. 4851–4865.
- Chen Der-San, Batson R.G., Dang Yu. Applied Integer Programming: Modeling and Solution. USA, NY, John Wiley and Sons Publ., 2010, 490 p.
- Vorobovich N.P., Lopateeva O.N. On NP-completeness of university timetable forming problems. The Bull. of KrasGAU, 2006, no. 11, pp. 385-391 (in Russ.).
- Valkovsky V.B., Belyaev S.А. Using phase transitions in solving combinatorial problems. Software & Systems, 2000, no. 4, pp. 37–38 (in Russ.).
- Valkovsky V.B., Belyaev S.А. Intelligent return in phase transition when solving combinatorial problems. Software & Systems, 2002, no. 4, pp. 16–19 (in Russ.).
- Razumovsky G.V., Pavlovsky М.G., Belyaev S.А. Сurrent calendar planning in decision support systems. Proc. of Saint Petersburg Electrotechnical Univ., 2007, no. 2, pp. 57–61 (in Russ.).
- Garey M.R., David S.J. Computers and Intractability: A Guide to the Theory of NP-Completeness. USA, SF, W.H. Freeman Publ., 1978, 340 p.
- Larin R.М., Pyatkin А.V. Two-level assignment task. J. of Applied and Industrial Mathematics, 2001, no. 2, pp. 42–51 (in Russ.).
- Krupsky V.N. Introduction to Computational Complexity. Moscow, 2006, 128 p. (in Russ.).
- Chernaya О.S., Fedorova Yu.Yu., Belyaev S.А. Application of automated testing methods and means to check the quality of software systems for processing measurement information. Proc. of Saint Petersburg Electrotechnical Univ., 2013, no. 9, pp. 55–58 (in Russ.).
-
The Millennium Prize Problems. Available at: http://www.claymath.org/millennium-problems/
millennium-prize-problems (accessed June 20, 2020).
УДК 004.021
DOI: 10.15827/2311-6749.20.3.1
Разработка алгоритма приведения двухуровневой кооперативной задачи
о назначениях к задаче коммивояжера
А.М. Шевелева 1, студент, shevelevaam_work@mail.ru
Г.В. Разумовский 1, к.т.н., доцент, razumovsky@nicetu.spb.ru
1 Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»,
С-Петербург, 197376, Россия
Статья посвящена актуальной проблеме приведения одних NP-полных задач к другим. Основное внимание в работе авторы уделяют разработке алгоритма приведения двухуровневой кооперативной задачи о назначениях к задаче коммивояжера для поиска ее решения и перенесения результатов решения одной NP-полной задачи в другую, приведены краткие математические формулировки задач.
В статье описываются проблемы, связанные с приведением одних NP-полных задач к другим. Как образец рассматривается пример приведения задачи коммивояжера к задаче гамильтонова цикла, предлагается новый алгоритм приведения двухуровневой кооперативной задачи о назначениях к задаче коммивояжера, в котором решены существующие проблемы приведения, накладывающие ограничения на сами NP-полные задачи.
Разработанный алгоритм приведения исследуется на точность получения результата исходной
NP-полной задачи и вычислительную сложность. В работе математически доказывается, что алгоритм приведения не снижает точность получения решения двухуровневой кооперативной задачи о назначениях при точном решении задачи коммивояжера. На сами задачи не накладывается никаких ограничительных условий. Также приведено математическое доказательство полиномиальной вычислительной сложности разработанного алгоритма приведения.
Для программной демонстрации корректности работы разработанный алгоритм приведения был реализован на языке программирования Java, а также реализованы точные алгоритмы решения двухуровневой кооперативной задачи о назначении и задачи коммивояжера. На данной программе были проведены эксперименты с нахождением решений исходной NP-полной задачи с различным количеством входных данных и подтверждена корректность работы алгоритма приведения.
В работе описаны дальнейшие перспективы по исследованию данного направления.
Ключевые слова: задача коммивояжера, np-полнота, двухуровневая задача о назначениях, алгоритм приведения, точность приведения, вычислительная сложность.
Литература
- Коробов Д.А., Беляев С.А. Современные подходы к обучению интеллектуальных агентов в среде Atari // Программные продукты и системы. 2018. Т. 31. № 2. С. 284–290. DOI: 10.15827/0236-235X.122.284-29.
- Клейнберг Дж., Тардос Е. Алгоритмы: разработка и применение. СПб.: Питер, 2016. 800 с.
- Кук С.А. Сложность процедур доказательства теорем. М.: Мир, 1975. С. 5–15.
- Ruiz-Vanoye J.A., Pérez-Ortega J., Pazos R.A., Díaz-Parra O., Frausto-Solís J., Fraire Huacuja H.J., Cruz-Reyes L. Survey of polynomial transformations between NP-complete problems. J. of Computational and Applied Mathematics. 2011, vol. 235, iss. 16, pp. 4851–4865.
- Chen Der-San, Batson R.G., Dang Yu. Applied Integer Programming: Modeling and Solution. John Wiley and Sons Publ., 2010, 490 p.
- Воробович Н.П., Лопатеева О.Н. О NP-полноте задач формирования расписания в вузе // Вестн. КрасГАУ. 2006. № 11. С. 385-391.
- Вальковский В.Б., Беляев С.А. Использование фазовых переходов при решении комбинаторных задач // Программные продукты и системы. 2000. № 4. С. 37–38.
- Вальковский В.Б., Беляев С.А. Интеллектуальный возврат в условиях фазового перехода при решении комбинаторных задач // Программные продукты и системы. 2002. № 4. С. 16–19.
- Разумовский Г.В., Павловский М.Г., Беляев С.А. Оперативно-календарное планирование в системах поддержки принятия решений // Изв. СПбГЭТУ «ЛЭТИ». 2007. № 2. С. 57–61.
- Garey M.R., David S.J. Computers and Intractability: A Guide to the Theory of NP-Completeness. USA, SF, W.H. Freeman Publ., 1978, 340 p.
- Ларин Р.М., Пяткин А.В. Двухуровневая задача о назначениях // Дискретный анализ и исследование операций. 2001. № 2. С. 42–51.
- Крупский В.Н. Введение в сложность вычислений. М.: Факториал Пресс, 2006. 128 с.
- Черная О.С. Федорова Ю.Ю., Беляев С.А. Применение методов и средств автоматизированного тестирования для проверки качества программных комплексов обработки измерительной информации // Изв. СПбГЭТУ «ЛЭТИ». 2013. № 9. С. 55–58.
- The Millennium Prize Problems. URL: http://www.claymath.org/millennium-problems/millennium-prize-problems (дата обращения: 20.06.2020).
Comments