Большинство существующих радиолокационных станций (РЛС) используют фазокодоманипулированные (ФКМ) сигналы и сигналы с линейной частотной модуляцией (ЛЧМ). Они получают сигналы от целей с любыми скоростями, но не могут обнаружить те из них, которые летят с малыми скоростями на фоне пассивных помех (подстилающая поверхность (ПП), местные предметы, метеообразования и т.д.), так как сигнал от помех может превышать сигнал от цели [1].
Для обнаружения целей на фоне пассивных помех применяются системы селекции движущихся целей, например череспериодное вычитание, однако даже оно не позволяет с достаточной эффективностью обнаруживать цели с малыми скоростями на фоне пассивных помех. Поэтому для исключения влияния пассивных помех на производительность в большинстве существующих РЛС используется режекция [2]. Как правило, величина режекции составляет 30–50 м/с. Снижение этой величины приводит к росту уровня пассивных помех в приемном тракте. Такие РЛС обнаруживают самолеты, ракеты и другие цели. Однако в последнее время большую роль в воздухе играют беспилотные летательные аппараты, скорость полета которых составляет от 10 до 50 м/с. Для обнаружения малоскоростных и маловысотных целей пригодны квазинепрерывные сигналы (КНС). Они обладают лучшими характеристиками по сравнению с ЛЧМ и ФКМ сигналами, но имеют неоднозначное определение дальности до цели [3].
Эта задача может быть решена путем выбора параметров КНС [4].
При решении задачи обнаружения дальность действия РЛС является дальностью ее обнаружения.
Поэтому под дальностью обнаружения (действия) будем понимать максимальное расстояние до цели, на котором она обнаруживается с заданными показателями качества – условными вероятностями правильного обнаружения D и ложной тревоги F.
Рассмотрим простейший случай обнаружения цели в свободном пространстве, то есть без учета влияния атмосферы и Земли.
Пусть в некоторой точке пространства на расстоянии rц от РЛС в направлении ε, β находится цель с эффективной площадью рассеивания (ЭПР) σц. При излучении зондирующих сигналов РЛС создает в месте расположения цели плотность потока мощности:
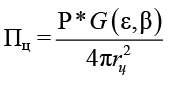 (1)
(1)
где Р – мощность передатчика РЛС (для импульсной РЛС – импульсная Ри); G(ε, β) – коэффициент усиления передающей антенны,
![]() .
.
Из-за воздействия электромагнитной энергии облучаемая цель становится вторичным излучателем. Мощность его излучения
Рц = Пц σц,
где σц – ЭПР цели,
![]()
В месте расположения приемной антенны такой источник создает плотность потока мощности:
![]() (2)
(2)
На вход приемника поступает сигнал мощностью
![]() (3)
(3)
где Аэфф(ε, β) – эффективная площадь приемной антенны.
Подставив соотношения в формулы (1–3), получим:
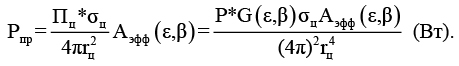
Переходя от мощности излученного и принятого сигналов к их энергиям, можем записать:
![]()
Для импульсных РЛС Э = Эи = Ри*τи, где Ри, τи – мощность и длительность импульса.
Заменим в формуле Эпр на пороговую Эпор (или минимально необходимую Эпр min), которая требуется для обнаружения цели с заданными показателями D и F. В этом случае вместо rц следует подставить rц max – максимальную дальность обнаружения, то есть
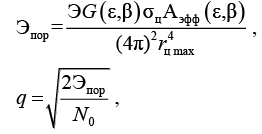
где N0 = kТ(Ш + tз – 1), k = 1,38*10-23 Дж/град; Т – абсолютная температура в градусах Кельвина (обычно принимают Т = 300 К); Ш – коэффициент шума приемника; tа = Та/Т – относительная шумовая температура антенны, Та – абсолютная шумовая температура антенны.
При tа = 1 или Ш > (tа – 1) получим
N0 = kTШ.
Радиальной скоростью Vr называют проекцию вектора V скорости цели на направление «измерительная система–цель». Так как Vr = dR/dt (где R – расстояние между измерительной системой и целью), в принципе, Vr можно определить, дифференцируя показания радиодальномера либо оценивая конечную разность дальностей на границах фиксированного интервала времени. Однако обычно для измерения скорости Vr используется эффект Доплера. Он проявляется в изменении частоты отраженного от движущейся цели сигнала fс относительно частоты f0 излучаемого сигнала РЛС. Разность частот излученного и принятого колебаний называется доплеровским приращением частоты Fд:
fс = f0 ± Fд.
Измеряя величину Fд, можно определить радиальную скорость:
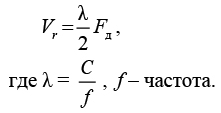
Если передатчик излучает гармонические колебания частоты fд, а приемник движется относительно него с переменной скоростью V(t) под углом Θ(t) к линии передатчик–приемник, для большинства практических приложений зависимость f0r от скорости V(t) с удовлетворительной точностью может быть определена простым соотношением:
![]()
где Vr(t) – радиальная составляющая скорости; λ – длина волны излучаемых колебаний.
В частном случае прямолинейного равномерного движения, когда V(t) = V0 = const, формула для fд упрощается:
![]()
Другими немаловажными характеристиками, определяющими возможности РЛС по обнаружению целей, являются минимальная и максимальная скорость обнаруживаемых целей, разрешающая способность РЛС по дальности, скорости и угловым координатам [5].
Разрешающая способность по дальности:
![]()
Потенциальная точность измерения дальности:
![]()
где qmin – минимальное отношение сигнал–шум по напряжению.
Разрешающая способность по скорости:
![]() .
.
Азимут:
![]()
где 0,5р – половина уровня мощности.
Угол места:
ε = 2Q0,5p.
Также необходимо учесть условие для обнаружения сигнала:
![]() ,
,
где Pw – мощность некоррелируемого шума на входе приемника: ![]() где N0 – энергия белового гауссова шума; Kr – коэффициент потерь приема; Pn – мощность помехи, Pn = k * Sn; Pc – мощность сигнала, Pc = k *
где N0 – энергия белового гауссова шума; Kr – коэффициент потерь приема; Pn – мощность помехи, Pn = k * Sn; Pc – мощность сигнала, Pc = k * Sc, Sn, Sc – эффективная площадь цели и помехи; qc – пороговое отношение сигнала (помеха + шум), ![]() , где F – вероятность ложной тревоги, D – вероятность правильного обнаружения,
, где F – вероятность ложной тревоги, D – вероятность правильного обнаружения, ![]() – коэффициент улучшения отношения сигнала:
– коэффициент улучшения отношения сигнала: ![]()
В данной работе были рассмотрены методы обнаружения малоскоростных и маловысотных целей на фоне ПП. Учитывая недостатки методов, использующих доплеровскую фильтрацию и пространственно-временную обработку, предложен подход, позволяющий обеспечить обнаружение малоскоростных
и маловысотных целей на фоне ПП за счет использования КНС с ЛЧМ несущей частоты.
Для достижения поставленной цели решается задача параметрической оптимизации КНС с ЛЧМ несущей частоты.
Такая возможность в помеховых условиях обеспечивается при условии минимизации интеграла свертки до уровня, при котором возможно обнаружение и целевых эхо-сигналов с требуемым качеством:
![]()
где 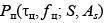 – мощность помехи на выходе подсистемы селекции движущейся цели (СДЦ) в канале приемообработки целевого эхо-сигнала с время-частотным сдвигом
– мощность помехи на выходе подсистемы селекции движущейся цели (СДЦ) в канале приемообработки целевого эхо-сигнала с время-частотным сдвигом 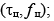
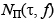 – энергетическая плотность распределения помехового фона на плоскости время-частотных сдвигов принимаемых локационных сигналов;
– энергетическая плотность распределения помехового фона на плоскости время-частотных сдвигов принимаемых локационных сигналов;
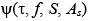 – функция время-частотной избирательности подсистемы СДЦ при использовании КНС S, которая в отличие от классической функции неопределенности (ФН) учитывает операцию их противопомеховой весовой обработки AS (бланкирование переходных процессов, режекторного выбеливания помехи и весовой аподизации).
– функция время-частотной избирательности подсистемы СДЦ при использовании КНС S, которая в отличие от классической функции неопределенности (ФН) учитывает операцию их противопомеховой весовой обработки AS (бланкирование переходных процессов, режекторного выбеливания помехи и весовой аподизации).
В отсутствие учета противопомеховой весовой обработки AS аналитическая запись ФН КНС с ЛЧМ имеет вид
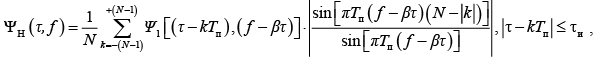
где 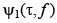 – ФН одиночного радиоимпульса КНС;
– ФН одиночного радиоимпульса КНС;
k – нумерация равноотстоящих максимумов ФН на временной оси 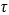 ; Тп, Fп – соответственно период и частота следования импульсов КНС;
; Тп, Fп – соответственно период и частота следования импульсов КНС; 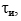 , N – соответственно длительность и суммарное количество радиоимпульсов КНС; β – скорость (крутизна) ЛЧМ несущей частоты КНС.
, N – соответственно длительность и суммарное количество радиоимпульсов КНС; β – скорость (крутизна) ЛЧМ несущей частоты КНС.
Исходная ФН КНС характеризуется решетчатой многопиковой структурой типа «борона». С вводом ЛЧМ несущей КНС ее ФН по отношению к исходной ФН немодулированной КНС характеризуется сдвиговой деформацией. С физической точки зрения требуется подобрать параметры КНС, при которых взаимопересечение высокоуровневых участков ФН КНС и области интенсивного помехообразования было минимальным.
Примерная гауссовская модель функции спектральной плотности помеховых отражений:
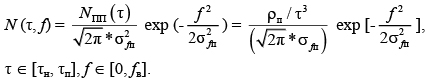
С учетом весовой обработки КНС (Аs) упрощенная аналитическая гауссовская модель квадратированной огибающей спектрального сечения центральной диагонали ФН КНС с ЛЧМ несущей имеет вид
![]()
где 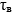 – верхняя граница контролируемого интервала временных задержек целевых эхо-сигналов;
– верхняя граница контролируемого интервала временных задержек целевых эхо-сигналов; 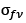 – эффективная ширина главного и боковых частотных максимумов ФН КНС с учетом весовой обработки (Аs).
– эффективная ширина главного и боковых частотных максимумов ФН КНС с учетом весовой обработки (Аs).
Энергетический уровень помехового сигнала на выходе радиоприемного канала (РПрК) для обнаружения целевых эхо-сигналов с параметрами 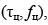 , создаваемого отражениями от ПП, определяется как
, создаваемого отражениями от ПП, определяется как
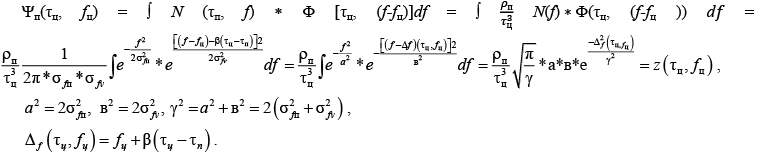
В режиме квазинепрерывного импульса (КНИ) с применением ЛЧМ имеет место радиоприем ПП не с одного, а с нескольких дальностных элементов разрешения, так как ![]()
Тогда суммарный помеховый фон, создаваемый отражениями с нескольких дальностных элементов разрешения
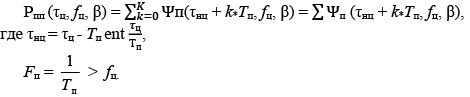
Основной энергетический вклад в помеховый фон приходится на ближайший к РЛС участок помеховых отражений в пределах единичного элемента разрешения по дальности. В качестве последнего примем дальностный элемент разрешения на ближней границе контролируемого диапазона временных задержек ![]() .
.
Тогда с учетом малочисленности К < 2, …, 3 в худшем с точки зрения маскирования целей ПП случае в первом приближении можно положить
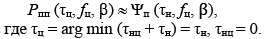
Из практики создания и эксплуатации радиолокационной техники известен факт существования технического предела в реализации больших значений коэффициента подавления пассивных помех: 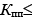 60…80 дБ.
60…80 дБ.
Применительно к рассмотренному случаю обнаружения малоскоростных целей это ограничение в формализованном виде можно представить как
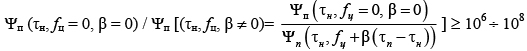
Далее решается задача нахождения частоты повторения импульса методом геометрических построений.
Но при этом сохраняется неоднозначность измерений, для устранения которых необходимо применять специальные математические методы обработки принимаемых сигналов.
Анализ методов по устранению неоднозначности измерений, таких как простейший метод устранения неоднозначности измерений, метод максимального правдоподобия, метод, основанный на китайской теореме об остатках, и метода перебора возможных решений показал, что это возможно сделать, используя сигналы специального вида, а также строгие математические зависимости на основе результатов нескольких измерений с различными параметрами зондирующего сигнала.
Для решения задачи используется китайская теорема об остатках, так как она проста в реализации
и поможет устранить неоднозначность измерений.
Китайская теорема об остатках оперирует с целыми числами, поэтому, чтобы взглянуть на поставленную задачу в ее свете, необходимо свести задачу к уравнениям в целых числах.
Сначала составим систему уравнений:
x = a1(modm1),
x = a2(modm2),
x = an(modmn).
Далее находим М0 – произведение всех делителей, то есть М0 = m1*m2*mn.
Ищем Mi по формуле Mi = M0/Mi.
После этого составляем новую систему уравнений: Miyi = ai(modmi). Из этого уравнения можем найти y. Ответ будет следующим: ![]()
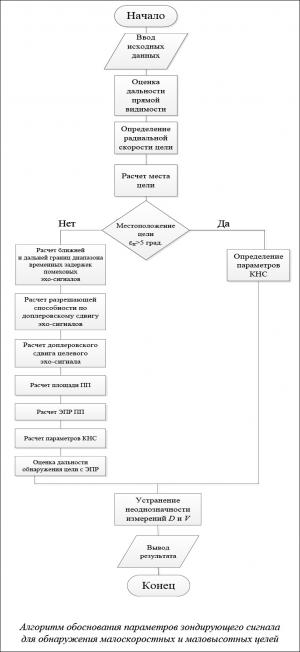
На основе всего этого был разработан алгоритм обработки зондирующего сигнала для обнаружения малоскоростных и маловысотных целей на фоне ПП, обеспечивающего устранение неоднозначности измерений.
Алгоритм обоснования параметров зондирующего сигнала для обнаружения малоскоростных и маловысотных целей приведен на рисунке.
Первый шаг описываемого алгоритма начинается с записи исходных данных, таких как разрешающая способность по дальности и скорости, ЭПР цели, угол места и азимут, длина волны, чувствительность приемника. Затем оценивается дальность прямой видимости, определяется радиальная скорость цели и рассчитывается угол места цели. Для обоснования параметров зондирующего сигнала, обеспечивающего снижение скорости обнаруживаемых целей, возможен процесс обнаружения целей без учета ПП и местных предметов. На практике это возможно при углах места цели больше 5 градусов. Если выполняется это условие, определяются параметры КНС.
В случае нахождения цели в точке с углом места менее 5 градусов необходимо уже учитывать влияние ПП и местных предметов для обнаружения цели.
Использование КНС позволяет добиться высоких показателей качества РЛС при обнаружении маловысотных и малоскоростных целей как в свободном пространстве, так и на фоне ПП и местных предметов, однако остается необходимость устранения неоднозначности измерения координат цели, обусловленной особенностью КНС. Неоднозначность измерений устраняется с помощью китайской теоремы об остатках.
Литература
- Бахвалов В.Б., Жуков С.А., Порошин С.М., Хомяков О.Н. Радиолокационная станция обнаружения маловысотных малоскоростных целей на фоне помеховых отражений от земли: пат. 2040008; Рос. Федерация. № 5041352/09; заявл. 06.05.1992; опубл. 20.07.1995. URL: http://www.findpatent.ru/patent/204/2040008.html (дата обращения: 18.01.2017).
- Панин Б.А., Лапидовская Т.М. Устройство селекции маловысотных малоскоростных воздушных целей и движущихся наземных целей в когерентной бортовой радиолокационной станции: пат. 2298809; Рос. Федерация. № 2005130543/09; заявл. 04.10.2005; опубл. 10.05.2007. URL: http://bd.patent.su/2298000-2298999/pat/servl/servletaeb7.html (дата обращения: 18.01.2017).
- Образцов Е., Пушков О. Маловысотные РЛС: шаг за шагом // Воздушно-космическая оборона. 2012. URL: http://www.vko.ru/oruzhie/malovysotnye-rls-shag-za-shagom (дата обращения: 10.04.2017).
- Гейстер С.Р., Куренев А.В. Методика определения параметров радиолокационного зондирующего сигнала // Докл. БГУИР. 2006. № 4. С. 11–16. URL: https://www.bsuir.by/m/12_100229_1_57915.pdf (дата обращения: 10.04.2017).
- Скосырев В.Н. Методы обзора пространства в современных многофункциональных РЛС // Наука и образование. 2014. № 12. URL: http://cyberleninka.ru/article/n/metody-obzora-prostranstva-v-sovremennyh-mnogofunktsionalnyh-rls (дата обращения: 10.04.2017).
Comments