Математические модели объектов химической технологии обладают явно выраженными иерархическими свойствами, что является отражением концептуальных воззрений на физико-химические процессы, происходящие в химико-технологическом процессе (ХТП). С другой стороны, с точки зрения теоретико-множественного подхода иерархия объектов – это порождение специального класса отношений порядка, называемого древесным.
Наиболее общим подходом, при котором отражается иерархическая взаимосвязь явлений, происходящих в процессах химической технологии, является подход, построенный на идеях концептуального моделирования [1]. Положительная черта концептуального моделирования – возможность достаточно простого подхода к оценке состояний и, соответственно, к оценке безопасности ХТП. Фактически каждый элемент процесса является источником опасностей, присутствующих в химико-технологической системе (ХТС), поэтому построение моделей древовидной структуры процессов соответствует структуризации опасностей, что позволяет с формальных позиций в целом оценить технологическую безопасность ХТП.
В качестве объекта концептуального моделирования в работе рассматривается технология выпаривания при производстве хлора и каустика.
Многокорпусные выпарные установки производства хлора и каустика – сложные объекты химической технологии
Объектом исследования выбрана четырехкорпусная выпарная установка, действующая в цехе выпарки хлорного производства Новомосковского химического комбината, а потому весь приводимый в работе статистический материал взят из опыта эксплуатации именно этого цеха. Данная технология выпаривания является примером типового процесса, постоянно применяемого при производстве хлора и каустика. Обобщенная структурная схема технологии выпаривания приведена на рисунке 1.
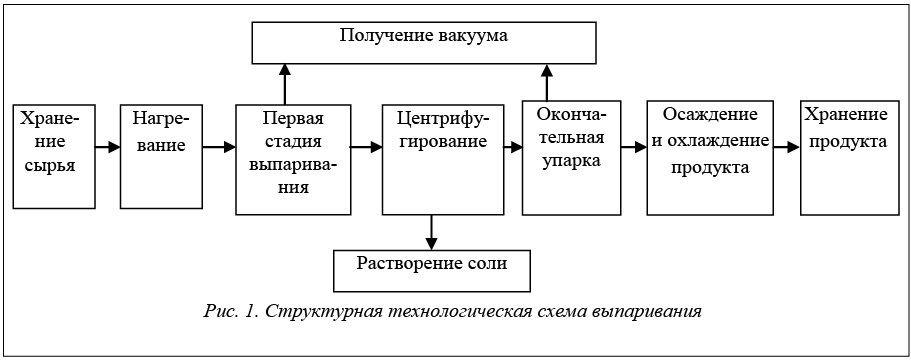
Многокорпусные выпарные установки (МВУ) широко распространены в различных отраслях промышленности (химической, пищевой, металлургической и др.), поэтому существует большое разнообразие конструкций, типов выпарных аппаратов (ВА), технологических схем выпарных станций и систем управления ими. Несмотря на это, они, за небольшим исключением, состоят из следующих элементов: ВА, конденсаторов смешения и поверхностных теплообменников, термокомпрессоров, конденсатоотводчиков, насосов, а на хлорных заводах необходимым элементом МВУ являются также центрифуги, растворители и осадители соли. Это обусловлено потребностью отделения выпадающей в осадок соли NaCl из раствора электролитической щелочи NaOH и готового продукта. Основным элементом выпарной системы является ВА, в котором происходят конденсация пара в греющей камере, передача тепла через стенку поверхности нагрева к кипящей жидкости, кипение жидкости.
Различные процессы, протекающие в выпарной установке, находятся в тесной взаимосвязи. Всевозможные возмущения, поступающие на вход всей системы и в отдельный аппарат (изменения концентрации и температуры поступающей на выпарку электролитической щелочи; давления и температуры
греющего пара; вакуума; коэффициента теплопередачи из-за засоления поверхности нагрева греющей камеры; отказ элемента аппаратуры или системы управления и т.д.), вызывают изменение выходных
параметров.
Например, изменение температуры греющего пара вызывает изменение количества тепла, передаваемого поверхности нагрева. При этом меняется температурный напор, а это приводит к изменению режима кипения и расхода вторичного пара.
Для повышения экономичности выпарки в производстве хлора и каустика применяются прямоточная схема с трехкратным использованием тепла свежего пара и концевые аппараты с усиленной естественной циркуляцией, обеспечивающие снижение расхода пара. В связи с необходимостью промежуточного выделения выпадающей в осадок соли третий корпус выпарной системы установки, работающий под вакуумом, состоит из двух аппаратов, включаемых по пару параллельно, а по щелочи последовательно.
Слабая электролитическая щелочь концентрацией 115–140 г/л NaOH, поступающая из цеха электролиза, собирается в сборники склада слабых щелоков. Из сборников центробежными насосами, установленными на складе, электролитическая щелочь подается в промежуточные баки, из которых под давлением около 10 атм центробежными насосами через подогреватели (где слабая щелочь нагревается до температуры 85–95 оС за счет использования тепла конденсата) подается в первые корпуса выпарных систем, представляющие собой выпарные аппараты с подвесной греющей камерой с поверхностью нагрева 450 м2.
Для поддержания рабочего давления в греющей камере первого корпуса в пределах 9–10 ати на линии входа свежего пара установлен регулятор давления. При выпаривании воды из раствора электрощелочи получается соковый пар давлением 5–6 ати и концентрация щелочи повышается до 200–220 г/л NaOH. Соковый пар первого корпуса поступает в греющую камеру второго корпуса. Из первого корпуса электролитическая щелочь самотеком, вследствие разности давлений, периодически перетекает во второй корпус. Концентрация щелочи во втором корпусе поддерживается в пределах 250–300 г/л NaOH. При этом происходит частичное выпадение кристаллов NaCl из раствора. Раствор вместе со взвешенной поваренной солью перепускается в третий корпус.
Соковый пар второго корпуса поступает в греющие камеры третьего и четвертого ВА, выполненных с подвесной греющей камерой и выносной зоной кипения. Поверхность нагрева в каждом из них 230 м2.
В третьем аппарате раствор упаривается до концентрации щелочи 350–420 г/л (средняя щелочь).
При этом происходит интенсивное выделение кристаллов соли NaCl из раствора. После отделения
соли на центрифугах (далее соль растворяется и рассол подается в цех электролиза) раствор средних щелоков сливается в приемники, из которых насосами через промежуточные сборники перекачивается
на окончательную упарку в четвертый аппарат. Раствор электролитических щелоков здесь упаривается до конечной концентрации 620–780 г/л NaOH (что соответствует 42–50 % NaOH), автоматически передается насосом в баки-отстойники и затем на склад готовой продукции.
Третий и четвертый аппараты работают под вакуумом не менее 640 мм рт. ст. Соковый пар из них, проходя через пенный промыватель, предназначенный для улавливания брызг щелочи, поступает в барометрический конденсатор, где смешивается с холодной промышленной водой, конденсируется, и
горячая вода стекает в барометрическую яму, а затем в канализацию. При конденсации греющего пара создается необходимое разряжение (не менее 640 мм рт. ст.).
Конденсат после первого и второго аппаратов, проходя через дросселирующие шайбы, смешивается с соковым паром соответствующих корпусов. Конденсат после третьего и четвертого аппаратов используется для подогрева щелочи, поступающей на вход выпарной установки.
Таким образом, приведенное выше описание технологического процесса выпаривания каустической соды показывает, что процесс выпарки представляет собой сложную ХТС, включающую различные процессы, основные из которых тепловые, солеотделение (центрифугирование, осаждение), солерастворение, соответствующее аппаратурное оформление и систему управления. Вся совокупность процессов находится в тесной взаимосвязи и действует как единое целое для получения готового продукта – каустической соды.
Математическое описание технологических режимов работы выпарных аппаратов
Центральным звеном выпарной установки является последовательная цепь ВА, которые определяют эффективность работы всей МВУ. В связи с этим основное внимание при создании модели выпарной установки уделено моделям ВА. Все остальные процессы носят вспомогательный характер, и эффективность их работы определяется работой ВА.
С точки зрения технологической безопасности узким местом технологии выпаривания является процесс центрифугирования – отделение соли от раствора средних щелоков. Этот этап сопровождается частыми механическими отказами, поэтому в технологической схеме выпарки используются резервные центрифуги. Кроме того, все вышесказанное можно отнести и к работе насосов.
Все эти вспомогательные элементы, участвующие в работе технологии выпаривания и выполняющие функции разделения и транспорта веществ, работают в условиях повышенного давления, высоких температур и соприкасаются с агрессивной средой.
Учитывая влияние центрифуг и насосов на технологическую безопасность, в окончательной модели безопасности МВУ будет использована их статистическая модель, которая с методологической точки зрения позволит оценить состояние технологии, а также уровень технологической безопасности МВУ.
Далее рассмотрим построение математического описания ВА.
Динамические режимы. При создании математического описания, которое учитывает основные физико-химические закономерности процесса выпарки, принимались следующие допущения [2]:
– ВА – объект с сосредоточенными параметрами;
– теплота кристаллизации и концентрирования раствора, а также потери пара в окружающую среду малы;
– питающий пар, поступающий в МВУ, является насыщенным.
В ВА можно выделить три элемента: парожидкостное пространство, стенку греющей камеры и греющую камеру. При получении системы уравнений ВА в соответствии с вышепринятыми допущениями будем рассматривать для каждого элемента основные уравнения сохранения массы и энергии, как для объектов с сосредоточенными параметрами.
Рассмотрим основные уравнения для парожидкостного пространства.
Уравнение материального баланса:
dri/dt=(Si вх-Si вых+Si *вх-Si*вых-Wi–Firidhi/dt)/(Vi+Fihi), (1)
где i – номер аппарата; t – время, с; Fi – площадь сечения ВА, м2; Vi – объем ВА до верхней крышки греющей камеры, м3; hi – уровень электрощелоков над верхней крышкой греющей камеры, м; ri – плотность раствора внутри аппарата, кг/м3; Wi – массовый расход вторичного пара, кг/с; Si вх, Si вых – массовый расход электролитических щелоков на входе и на выходе, кг/с; Si *вх , Si *вых – массовый расход соли на входе и на выходе, кг/с.
Производная dri/dt прежде всего зависит от изменения концентрации внутри аппаратов щелочи bi вых и соли fi вых. Скорость изменения концентрации едкого натра и соли в ВА в несколько раз меньше скорости изменения температуры ti вых, поэтому колебания bi вых и fi вых сравнительно малы. И в то же время изменение температуры внутри аппаратов не настолько значительно, чтобы оказывать существенное влияние на изменение плотности. Таким образом, dri/dt с достаточной для практических расчетов точностью можно приравнять к нулю, и уравнение материального баланса будет иметь вид
dhi/dt=(Si вх-Si вых+Si *вх-Si *вых-Wi)/(Firi). (2)
Уравнение энергетического баланса парожидкостной системы имеет вид
dti/dt={Si вхci вхti вх+Fi²ki(ti вых-qi)-WiJiп-Si выхci выхti вых-
-(Vici выхti вых+Fici выхti выхhi)dri/dt-
-Fici выхriti выхdhi/dt-d(Vi*Ji пri п)/dt-Gi¢ci¢dti¢/dt- (3)
-Gi¢¢ci¢¢dti¢¢/dt}/(Vici выхri вых+Fici выхri hi),
где Fi² – площадь поверхности теплообмена со стороны парожидкостного пространства, м2; ki=1/(1/ai2+diп/liп) – коэффициент теплопередачи от электрощелоков к стенке, Вт/м2 оС; ai2, liп – коэффициент теплоотдачи от электрощелоков к стенке греющей камеры и коэффициент теплопроводности накипи, Вт/м2 оС и Вт/м оС соответственно; diп – толщина слоя накипи, м; qi – температура стенки теплообменника со стороны жидкости, оС; Vi* – объем сепарационного пространства ВА, м3; riп – плотность пара в сепарационном пространстве, кг/м3; Gi¢, Gi¢¢ – масса корпуса и изоляции ВА, кг/м3; ci¢, ci¢¢ – теплоемкость корпуса и изоляции, Дж /кг оС; ti¢, ti¢¢ – температура корпуса и изоляции, оС.
Ряд членов d(Vi*Jiпriп)/dt, Gi¢ci¢dti¢/dt, Gi¢¢ci¢¢dti¢¢/dt этого уравнения, которые характеризуют изменение энергии сепарационного пространства, корпуса и изоляции ВА, могут быть приравнены к нулю. Кроме того, из рассмотрения могут быть исключены члены, учитывающие теплоты кристаллизации NaCl и NaOH, а также члены более высокого порядка малости. Погрешность от этого исключения, особенно для первых трех аппаратов, невысока (не превышает 2–3 %, [3]).
В результате уравнение энергетического баланса запишется следующим образом:
dti/dt={Siвхciвхtiвх+Fi²ki(tiвых-qi)-WiJiп-Siвыхciвыхtiвых--Ficiвыхritiвыхdhi/dt}/(Viciвыхri+Ficiвыхri hi), (4)
Wi=0.
Если в ВА происходит установившийся процесс кипения, то производная dti/dt равна нулю и количество испарений можно определить по формуле
Wi={Siвхciвхtiвх+Fi²ki(tiвых-qi)-Siвыхciвыхtiвых-Ficiвыхritidhi/dt}/Jiп. (5)
С другой стороны, если температура внутри аппарата будет меньше температуры кипения, то количество испарений будет равно нулю. Такое разделение уравнения (3) на два уравнения позволяет проанализировать режимы пуска и останова ВА.
Уравнения материального баланса по сухому компоненту имеют следующий вид:
dbiвых/dt=(Si вхbiвх-Siвыхbiвых-Firibiвыхdhi/dt)/(Viri+Firi hi), (6)
dfiвых/dt=(Siвхfiвх-Siвыхfiвых+Siвх*-Siвых*-Firibiвыхdhi/dt)/(Viri+Firi hi). (7)
При составлении данных уравнений предполагалось, что унос щелочи NaOH и соли NaCl с паром отсутствует.
Уравнение энергетического баланса стенки греющей камеры имеет вид
dtiс/dt={Fi¢ki¢(tiвых-qiс)-Fi²ki²(qiс-tiк)}/(Giмсi м), (8)
где ki¢=1/(1/ai1+diс/(2liм)) – коэффициент теплопередачи от греющего пара к стенке, Вт/м2 оС; ki¢¢=1/(1/ai2+diс/(2liм)) – коэффициент теплопередачи от стенки к стенке, Вт/м2 оС; qiс – температура в средней точке стенки греющей камеры, оС; Fi¢ – площадь поверхности теплообмена со стороны греющего пара, м2; liм – теплопроводность стенки греющей камеры, Вт/м оС; ai1 – коэффициент теплоотдачи от греющего пара к стенке, Вт/м2 оС; diс – толщина стенки греющей камеры, м.
Предварительные расчеты математической модели показали, что переходные процессы в стенке греющей камеры протекают во много раз быстрее, чем в парожидкостном пространстве. Поэтому совместное решение записанных выше уравнений приводит либо к резкому увеличению продолжительности интегрирования, либо, в случае увеличения шага интегрирования, к неустойчивости процесса решения на вычислительной машине. По этой причине уравнение (8) исключили из рассматриваемой системы, изменив при этом уравнения (4) и (5):
dti/dt={Siвхciвхtiвх+Fi²ki(tiвых-tiп)-Siвыхciвыхtiвых-Ficiвыхritiвыхdhi/dt}/(Viciвыхri+Ficiвыхri hi), (9)
Wi={Siвхciвхtiвх+Fi²ki(tiвых-tiп)-Siвыхciвыхtiвых-Ficiвыхritiвыхdhi/dt}/Jiп. (10)
Следующим элементом ВА является греющая камера. Предварительные расчеты показали, что продолжительность процессов, протекающих в греющей камере, намного меньше продолжительности процессов, протекающих в парожидкостном пространстве, следовательно, как и в случае со стенкой греющей камеры, не имеет смысла решать совместно дифференциальные уравнения, описывающие состояние греющего пара и электрощелоков.
В силу допущения о равенстве потоков греющего пара на входе в греющую камеру и конденсата на выходе из нее уравнения материального баланса будут иметь вид
Diп=Diк, (11)
где Diп и Diк – массовые расходы греющего пара и конденсата соответственно, кг/с.
Статические режимы. Уравнения для статических режимов работы являются следствием уравнений динамики ВА.
Основными уравнениями математического описания, отражающего особенности статического режима работы, является совокупность уравнений энергетического баланса греющих камер и парожидкостного пространства ВА:
Diвх(J(i-1)п-J(i-1)к)-кiFi(tiконд-tiкип)=0, (12)
Siвхciвхtiвх+Fi²ki(tiконд-tiкип)-Siвыхciвыхtiвых-WiJiп=0, (13)
уравнения материальных балансов
Siвх-Siвых-Siвых*-Wi=0, (14)
Siвхbiвх-Siвыхbiвых=0, (15)
Siвхfiвх-Siвыхfiвых=0 (16)
и уравнения связи между аппаратами
Siвх–S(i-1)вых=0, (17)
biвх-b(i-1)вых=0, (18)
fiвх-f(i-1)вых=0, (19)
tiвх-t(i-1)вых=0. (20)
Формулы для расчета физико-химических свойств. Для выполнения расчетов по математической модели необходимо использовать ряд зависимостей для определения температур конденсации пара в греющих камерах, температур кипения электрощелоков в ВА, теплоты парообразования, энтальпии сокового пара, равновесной концентрации соли NaCl в растворе щелоков. Данные функции большей частью были получены на основе метода наименьших квадратов [3].
Температура конденсации греющего пара
tiконд=78,929+583,04(0,0034 Pi–0,0019)1/2, (21)
где Pi – давление греющего пара (0,7£Pi£12), ата. Данная зависимость также применяется для вычисления температуры сокового пара и в некоторых других случаях.
Температура кипения раствора в ВА, как функция концентрации щелочи NaOH и давления, определяется по табличным данным [4]:
tiкип=(95,35-34,94 bi+204,2 bi2)(0,421+0,269(7,437 Pi+0,465)1/2). (22)
Данная формула хорошо оценивает температуры кипения третьего и четвертого аппаратов. Для определения температуры в первом и втором корпусах используется метод Тищенко [5].
По этому методу температурная депрессия раствора при любом давлении может быть найдена по формуле
Dtp=fDtат, (23)
где Dtp – температурная депрессия при давлении P; Dtат – температурная депрессия раствора при атмосферном давлении; f – поправочный коэффициент, рассчитываемый по формуле
f=16,2 T2/r, (24)
где r – удельная теплота парообразования, Дж/кг; T – температура кипения чистой воды при заданном давлении, оК.
Температурная депрессия при атмосферном давлении определяется из формулы (24):
Dtат=12,21-41,15 bi+240,3 bi2. (25)
Используя формулу (23), легко вычислить T оК:
T=351,93+583,04(0,0034 Pi–0,0019)1/2. (26)
Для вычисления температуры кипения в первом и втором аппаратах, а также расчета уравнений тепловых балансов необходимо иметь функциональные зависимости теплоты парообразования от давления.
Данные функции были получены методом средних для технологических режимов работы каждого аппарата по таблицам свойств водяного пара в зависимости от давления (погрешность 2–3 %):
r=-80000P+2343000 (Дж/кг), 0,5£P£1,1 (ата), (27)
r=-45463P+2301222 (Дж/кг), 1,0£P£3,0 (ата), (28)
r=-22000P+2228000 (Дж/кг), 4,0£P£7,0 (ата), (29)
r=-15333P+2178333 (Дж/кг), 8,0£P£12 (ата). (30)
Методом средних получена зависимость энтальпии пара от давления:
J=2671125,0P0,02242 (Дж/кг), 1,0£P£11 (ата). (31)
Для аппроксимации табличных данных по равновесной концентрации соли NaCl в растворе щелочи NaOH, взятых из справочной литературы [6], получена формула (a=tiкип/100):
fiравн={[(-6,547a+28,9)a-37,74]a+43,878+{[(0,523a-2,264)a+
+3,262]a-2,464}100bi+{[(-0,0118a+0,052)a-0,0773]a+0,044}(100bi)2+{[(0,0001a-0,00041)a+0,000586]a-
-0,00025}(100bi)3}/100, (вес. %). (32)
Для расчета давлений в парожидкостных пространствах первого и второго ВА использовались эмпирические формулы, установленные на основе экспериментальных данных, взятых непосредственно с действующей установки:
Pпж1=0,9+0,45Pгп+1,067Pв, (33)
Pпж2=1,241+0,181Pгп+1,035Pв. (34)
На основе этих формул вычисляются наиболее вероятные значения давлений в парожидкостных пространствах при заданном вакууме в третьем и четвертом аппаратах и давлений греющего пара в первом корпусе.
Уравнения (1–34) позволяют рассчитать различные технологические режимы работы МВУ, и, учитывая это обстоятельство, математическая модель является необходимой в программном обеспечении системы управления (СУ) технологической безопасностью.
Характеристика технологической безопасности выпарной установки
Каждый объект химической технологии имеет свои специфические особенности с точки зрения технологической безопасности. Особенность технологии выпаривания состоит в том, что основная нагрузка по обеспечению безопасной работы выпарной установки ложится на обеспечение безотказной работы непосредственно технологического процесса выпаривания, профилактики отказов оборудования и СУ.
При наличии сбоев в работе МВУ влиянием на внешнее окружение можно пренебречь, за исключением катастрофических ситуаций (например террористический акт). При возникновении аварийных или различного рода нештатных ситуаций подвергается опасности персонал цеха. Возможны случаи небрежного отношения к правилам техники безопасности при работе со щелочью, а также различного рода механические поломки, приводящие к выбросу электролитических щелоков или греющего пара. Все это в конечном итоге сказывается на обслуживающем персонале или оборудовании цеха.
Следовательно, для обеспечения технологической безопасности необходимо исследовать опасности, исходящие непосредственно от технологического процесса, от оборудования, от СУ.
Опасности, исходящие от технологических процессов, для объектов химической технологии проявляются в изменении констант скоростей химических реакций, коэффициентов диффузии, коэффициентов теплоотдачи, изменении свойств катализаторов и т.д. Чем продолжительнее сохраняются необходимые значения параметров, тем меньше остановок как на плановые, так и внеплановые ремонты. Соответственно, более надежно с точки зрения технологической безопасности работает ХТС.
При описании опасностей, исходящих от оборудования и систем управления, необходимо учитывать, с одной стороны, соблюдение требований техники безопасности, которые предъявляются обслуживающему персоналу цеха при выполнении различных видов работ, с другой – надежностные свойства машин и аппаратов и СУ. Такой подход увеличивает число управляющих воздействий, но повышает неопределенность в принятии решений.
При описании надежностных свойств, характерной чертой которых является наличие двух качественно отличных видов отказов, используются два подхода:
– функциональный, учитывающий выполнение определенной функции отдельным элементом ХТС; обычно функциональный подход приводит к необходимости анализировать внезапные отказы (их называют постоянными), а также сбои, или кратковременные отказы; отличительная особенность сбоя проявляется в его способности самоустраняться;
– эффективностный, рассматривающий поведение показателя эффективности с течением времени в зависимости от временных изменений технологических параметров системы; данный подход в основном анализирует постепенное изменение одного или нескольких параметров объекта.
Из приведенных выше рассуждений следует, что основным показателем безопасной работы ВА являются коэффициенты теплопередачи. Коэффициенты теплопередачи не только характеризуют тепловой режим работы ВУ, но и являются показателями безопасности технологического режима работы. Ухудшение с течением времени коэффициентов теплопередачи приводит к необходимости остановки ВА на промывки, что вызывает сбои технологического режима работы.
В работе [2] на основе пассивного эксперимента получены линейные функции временных изменений коэффициентов для второго, третьего и четвертого ВА:
k(t)2=803,17–31,68t, Вт/(м2 оС), (35)
k(t)3=722,88–4,049t, Вт/(м2 оС), (36)
k(t)4=898,21–7,455t, Вт/(м2 оС). (37)
Используя соотношения (1 – 37), можно получить дискретные модели на основе метода разделения состояний. Данные модели необходимо использовать в оценке состояний ВА и далее – в принятии решений по управлению МВУ. Построение дискретных моделей рассмотрим ниже.
Важными эксплуатационными характеристиками МВУ (не отдельных ВА) с точки зрения технологической безопасности являются не только коэффициенты теплопередачи (они необходимы в оценке
состояний отдельных ВА), но и функция удельных затрат, которая характеризует математическое ожидание потерь греющего пара от эффективностных (постепенных) отказов.
В процессе эксплуатации ВУ в ней происходят изменения, в результате которых изменяются состояния, в которых находится система. В каждом из состояний система может выполнять заданные функции с определенным уровнем качества. Вид показателя качества функционирования и его значение во многом определяются видом решаемой задачи, завися от цели, которой стремятся достигнуть.
Для определения значений показателя качества функционирования рассматривают результаты
применения системы по назначению. При этом обычно приходится учитывать воздействие на систему случайных факторов. В результате показатели качества функционирования обычно являются
характеристиками случайных событий, величин, процессов.
Количественная оценка качества функционирования зависит от состояния системы в данный момент времени и в общем случае может зависеть от всех предшествующих состояний системы, то есть от траектории эволюции системы. Значения количественной оценки качества функционирования являются мгновенными оценками работы системы в определенные моменты времени.
Поскольку состояния системы могут изменяться со временем случайным образом и система может подвергаться внешним случайным воздействиям, оценка качества функционирования является случайным процессом. Наиболее часто в качестве показателей качества функционирования применяются математические ожидания случайных величин.
При непрерывной работе МВУ с течением времени по ряду причин происходит ухудшение условий работы, среди которых загрязнения поверхностей греющих камер, трубопроводов, технологической аппаратуры, а также снижение качества работы СУ (объясняемое наличием процессов кристаллизации соли, высокими температурами и агрессивностью среды). Ухудшение условий технологического режима работы находит свое выражение в увеличении затрат, среди которых наибольший вес занимают затраты на греющий пар. В качестве показателя эффективностного (постепенного) отказа целесообразно использовать функцию удельных затрат, оценка которой по результатам пассивного эксперимента показывает, что в данном случае функция удельных затрат Собщ зависит от времени пробега выпарной линии с момента последнего текущего ремонта Dt и от мгновенной нагрузки S(t). Зависимость удельных затрат имеет вид [2]:
Собщ=5,32[27,474-393,75(S(t)/1000)+1534,2(S(t)/1000)2][1,14-0,097exp(-0,0108Dt)], (руб./(дни(тонн100%NaOH))). (38)
Результаты расчетов показали, что функция удельных затрат имеет по нагрузке электрощелоков явно выраженный экстремум, а по продолжительности работы МВУ со времени последнего текущего ремонта затраты на пар вначале увеличиваются, затем уменьшаются. Это связано, видимо, с тем, что в начальный период происходит наиболее активное загрязнение выпарной установки, затем этот процесс устанавливается.
При управлении технологической безопасностью необходимо знать статистические закономерности функциональных отказов (внезапные отказы, сбои). Поясним более подробно понятие функционального отказа. МВУ состоит из ряда взаимосвязанных элементов, каждый из которых выполняет определенную функцию, поэтому отказ какого-либо элемента приводит к нарушению соответствующей функции и называется функциональным. Большинство функциональных отказов приводит к экстренным остановкам линии или отдельных ее участков на ремонт.
Наиболее полная и достоверная оценка информации по функциональным отказам может быть получена только по результатам экспериментального исследования отказов аппаратов и СУ в реальных условиях эксплуатации. Необходимо отметить, что основной трудностью в проведении данного статистического исследования является ограниченность и неупорядоченность информации о процессе эксплуатации МВУ. Получение достоверной экспериментальной оценки по надежности требует наличия достаточного по объему исходного статистического материала, что связано с большой затратой времени и средств.
Результаты статистического исследования по основным элементам оборудования и СУ (табл. 1, 2) показывают, что в большинстве своем аппроксимация законов распределения безотказной работы экспоненциальными законами является достаточно точной и согласуется с принятой гипотезой с доверительным уровнем 90–95 % [2].
Важным свойством экспоненциального закона является то, что вероятность безотказной работы системы в течение заданного промежутка времени не зависит от того, сколько времени система проработала до этого промежутка. Вероятность безотказной работы системы за равные промежутки времени будет одинаковой на протяжении всего периода нормальной эксплуатации независимо от того, в начале или в конце этого периода расположены промежутки.
Появление экспоненциального закона объясняется тем, что исследование МВУ проводится в период нормальной эксплуатации, который является основным этапом эксплуатации технологических систем. Длительность этого периода соизмерима с эксплуатационным сроком их службы, так как период приработки относительно невелик, а работа в период износа для большинства технологических систем недопустима, и они заменяются новыми. Характерной особенностью периода нормальной эксплуатации системы является постоянство интенсивности отказов элементов технологических систем, что подтверждается проведенными исследованиями надежностных свойств МВУ.
Необходимо отметить, что показательное распределение времени безотказной работы является довольно грубым приближением к действительности и его целесообразно использовать лишь в тех случаях, когда можно пренебречь влиянием износа. Допущение о том, что интенсивность отказов постоянна, аналогично предположению о неизменности физико-химических свойств материалов. В действительности все технические устройства изнашиваются и стареют.
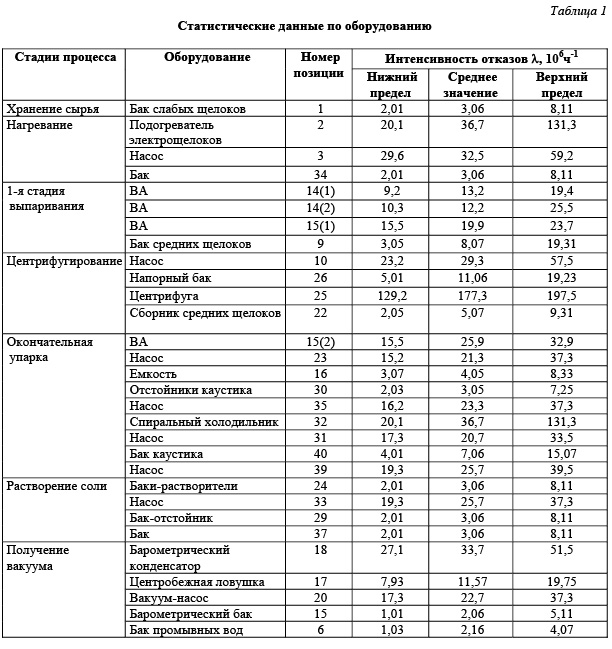
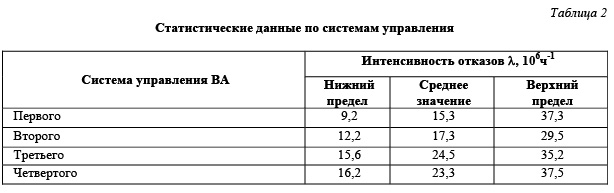
При составлении календаря, по которому производился первоначальный статистический анализ надежности элементов технологической схемы и СУ МВУ, в него заносились данные об отказах –
как вызвавших небольшие нарушения технологического режима работы, так и приводивших к продолжительным остановкам ВУ на ремонт. В частности, отказы СУ третьего и четвертого аппаратов не разделялись по отдельным системам автоматического регулирования. Их две: одна система регулирует
температурную депрессию по входному потоку электрощелоков, а вторая – выходной поток по уровню
в аппарате.
Анализ имеющейся информации позволил их классифицировать. Основным признаком классификации является продолжительность ремонта. В данном случае анализировались отказы, приводящие к текущему ремонту, обычная продолжительность которого составляет от одной смены до суток.
В результате такого статистического анализа было установлено, что время безотказной работы всей МВУ для данного типа отказов подчиняется нормальному закону (М(х)=39–45 суток, s(х)=10–15). Статистические выборки согласуются с принятой гипотезой с доверительным уровнем 95–97 %. Это позволило сделать вывод о том, что такие отказы носят усталостный характер и обусловлены действием высоких температур, агрессивностью среды, процессов солеосаждения и коррозии, протекающих в МВУ.
В заключение необходимо отметить, что приведенные данные по статистическому исследованию не являются универсальными, описывающими МВУ для любого хлорного производства. Многое определяется составом исходного сырья, поступающего на хлорное производство, некоторыми конструкционными отличиями аппаратурного оформления процессов, технологией работы цеха электролиза, временными интервалами работы цеха, для которых имеется в наличии статистический материал, места расположения предприятия, климатических условий работы и т.д.
Построение дискретных моделей ВА
Для построения дискретной модели ВА приведем основные уравнения материальных тепловых балансов, которые необходимо использовать для построения дискретных моделей:
Для построения дискретной модели ВА приведем основные уравнения материальных тепловых балансов, которые необходимо использовать для построения дискретных моделей:
dhi/dt=(Siвх-Siвых+Si*вх-Si*вых-Wi)/(Firi),
dbiвых/dt=(Siвхbiвх-Siвыхbiвых–Firibiвыхdhi/dt)/(Viri+Firihi),
Siвхbiвх-Siвыхbiвых=0,
dfiвых/dt=(Siвхfiвх-Siвыхfiвых+Siвх*-Siвых*-Firibiвыхdhi/dt)/ /(Viriвых+Firiвыхhi),
Siвхfiвх-Siвыхfiвых+Siвх*-Siвых*=0,
dti/dt={Siвхciвхtiвх+Fi²ki(tiп-tiвых)-WiJiп-Siвыхciвыхtiвых-Ficiвыхritiвыхdhi/dt}/(Viciвыхriвых+Ficiвыхriвыхhi),
Siвхciвхtiвх+Fi²ki(tiп-tiвых)-Siвыхciвыхtiвых-WiJiп=0.
Прежде чем в соответствии с методом разделения состояний записать неравенства, рассмотрим некоторые члены вышеприведенных уравнений.
Члены Viri+Firihi и Viciвыхri+Ficiвыхri hi являются оценками вещества и количества тепла, которые сосредоточены в парожидкостном пространстве ВА для конкретного момента времени.
Элементы Viri и Viciвыхri характеризуют постоянную составляющую и в основном зависят от компонентного состава и температуры. (По аксиоматическим допущениям, которые были введены при построении математической модели, температура и давление в данном процессе жестко связаны, поэтому,
говоря о температуре, подразумевают и связь по давлению.) Так как температура и компонентный состав для нормального технологического режима мало меняются, их можно считать константами.
Элементы Firi hi и Ficiвыхrihi в первом приближении характеризуют переменную составляющую – это количество массы вещества и тепловой энергии, сосредоточенной над верхней крышкой греющей камеры. Их изменения связаны с изменением параметра hiго. Действительно, при работе ВУ постоянно происходят мгновенные изменения уровня в ВА. Это связано с применяемыми системами регулирования уровня в аппаратах. Эти системы отличаютс между собой. В первых двух аппаратах используются позиционные системы регулирования (раствор поступает порциями в данные аппараты в зависимости от состояния замкнутости или разомкнутости электродов САР), в третьем и четвертом применяются непрерывные регуляторы (раствор поступает непрерывно в зависимости от температурной депрессии в ВА).
Необходимо отметить следующее: проведенные исследования показывают, что зависимость коэффициента теплопередачи от уровня раствора в ВА носит экстремальный характер, поэтому определенного увеличения производительности можно достичь экстремальным регулированием уровня. На практике это достигается на основе обобщения опыта работы обслуживающего персонала.
Из вышеприведенного следует:
– для первых двух аппаратов колебания уровня происходят в диапазоне верхней и нижней позиций электродов (10–15 см) системы регулирования уровня этих аппаратов, то есть практически можно считать уровень постоянным;
– для третьего и четвертого аппаратов уровень поддерживается непрерывной системой и является статистически постоянной величиной, то есть присутствуют колебания уровня около некоторой постоянной величины, определяемой динамикой системы управления, не превышающие 5–10 % от задания.
Таким образом, члены Viri+Firihi и Viciвыхri+Ficiвыхrihi можно считать постоянными для нормального режима эксплуатации ВУ. Для исключения спорадического характера диагноза состояния по дискретной модели при попадании параметров технологического режима процесса на границу разделения режимов необходимо ввести пороговый уровень доверия. Кроме того, введение порогового уровня доверия компенсирует погрешности вычислений по модели, связанные с вышеуказанными допущениями.
Запишем основные ограничения дискретной модели:
Siвхbiвх-Siвыхbiвыхmax<Dbiвых(k), (39)
Siвхbiвх-Siвыхbiвыхmin>Dbiвых(k), (40)
Siвхfiвх-Siвыхfiвыхmax+Siвх*-Siвых*<Dfiвых(k), (41)
Siвхfiвх-Siвыхfiвыхmin+Siвх*-Siвых*>Dfiвых(k), (42)
Siвхciвхtiвх+Fi²ki(tiп-tiвыхmax)-Siвыхciвыхtiвыхmax-WiJiп<Dtiвых(k), (43)
Si вхciвхtiвх+Fi²ki(tiп-tiвыхmin)-Siвыхciвыхtiвыхmin-WiJiп>Dtiвых(k). (44)
Из приведенных соотношений видно, что для работы дискретной модели нужно знать Siвх, Siвых, biвх, biвых, fiвх, fiвых, t iвх, tiвых, Wi. Здесь необходимо отметить, что часть этих параметров измеряется непосредственно на ВУ-установке. Это относится к концентрации щелочи и соли в растворе электрощелоков. Остальные параметры определяются расчетным путем на основе данных, взятых с ВУ: расхода и давления греющего пара, давлений в ВА, температурной депрессии. Кроме того, используются формулы, приведенные ранее для расчета физико-химических свойств электрощелоков.
Построение концептуальной модели выпарной установки
В данной работе проводится строгое соответствие между процессами, конструкциями, аппаратами и опасностями, порождаемыми ими. При таком подходе на начальном этапе введем на множество опасностей отношение «принадлежать определенному объекту (процессу)». В результате множество опасностей разбивается по параметрам (рис. 2): сырья; энергии (электро-, тепло- и т.д.), участвующей в процессе; непосредственно химико-технологическим, происходящим в объеме аппаратов; оборудования; СУ.
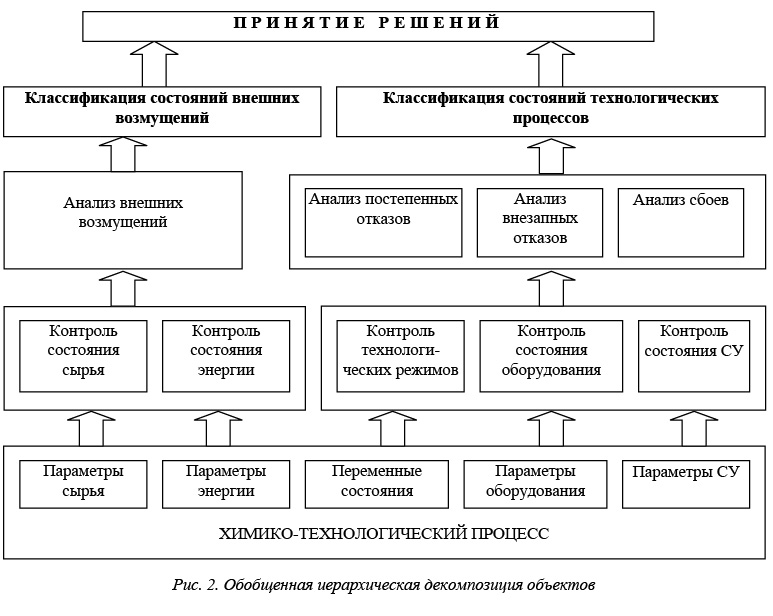
Для локализации опасностей необходим контроль вышеназванных объектов с последующей оценкой их состояния и принятием управляющих решений. Практическая реализация указанных процессов иллюстрируется на рисунке 3, где показана организационная составляющая (иерархия исполнителей), реализующая в процессе эксплуатации МВУ диагностику состояний как отдельных элементов технологической последовательности, так и всей системы в целом.
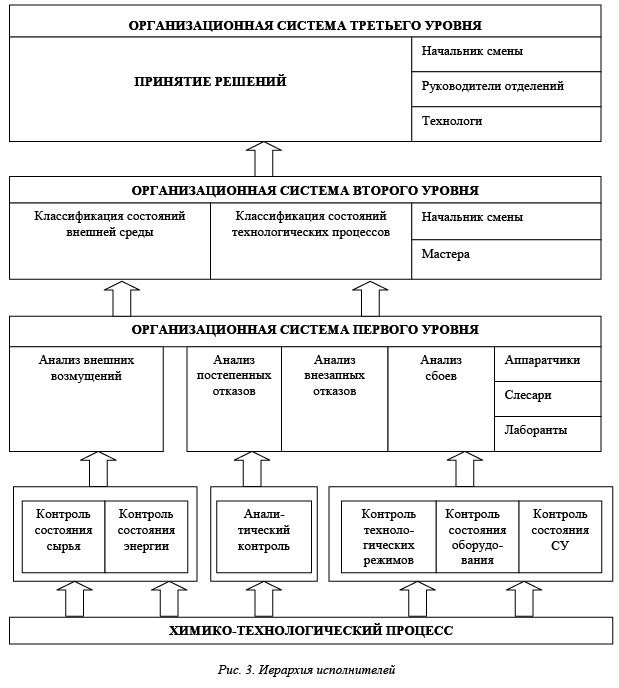
По отношению «принадлежать определенному объекту (процессу)» получаем разбиение универсального множества опасностей на подмножества опасностей, принадлежащих к конкретным технологическим объектам. Такая декомпозиция позволяет на начальных этапах в какой-то мере сузить и упростить анализ опасностей.
В то же время если для каждого полученного объекта продолжить декомпозицию на основе такого же отношения «принадлежать определенному объекту (процессу)», то получим разбиение множества опасностей по отдельным подобъектам ранее выделенных объектов.
Формально этот процесс декомпозиции можно представить следующим образом.
Пусть имеется некоторое первоначальное разбиение универсального множества опасностей О системы S на подмножества Oi: О={Oi}, i=1, …, N, где N – общее число опасностей системы S (мощность множества О). Разбиение множества проведено так, что подмножества опасностей не пересекаются: О=ÈOi, i=1, …, N; OiÇOj=Oi, если i=j; OiÇOj=Æ , если i¹j.
Такое разбиение соответствует разбиению системы S на подсистемы {Si}, i=1, …, N. Если продолжить разбиение каждого Si на отдельные составляющие Si {Sij}, j=1, …, K, ставя при этом каждой из подсистем свое подмножество опасностей Оi={Oij}, j=1, …, K, то получим следующий уровень иерархии опасностей.
Данный процесс разбиения можно продолжить до уровня, который допускают наши знания о процессе или объекте, или до уровня, который диктуется требованиями, предъявляемыми к решению задачи управления технологической безопасностью.
Такой подход порождает древовидные структуры опасностей, служащие в дальнейшем базой исходной информации для проведения процедур оценки состояний технологической схемы, решения задачи прогноза и определения первопричин возникших нарушений и управления технологической безопасностью.
Для МВУ древесный порядок опасностей показан на рисунке 4. Каждый уровень опасностей характеризуется возможным возникновением нарушений технологических режимов работы, отказов или сбоев оборудования и СУ.
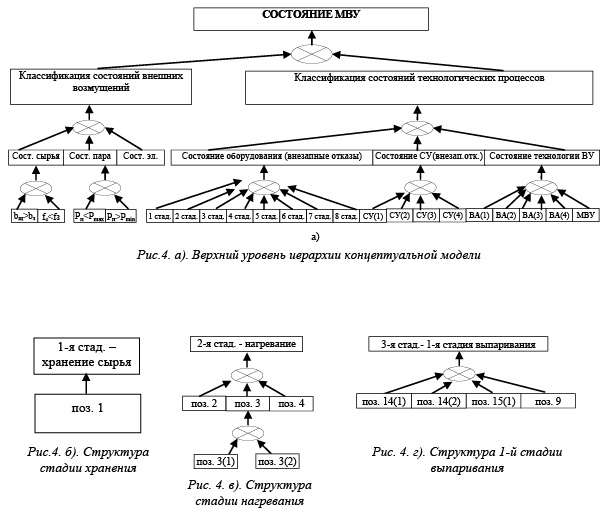
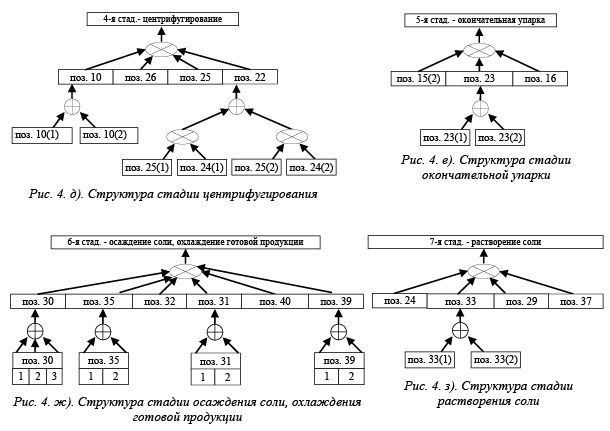
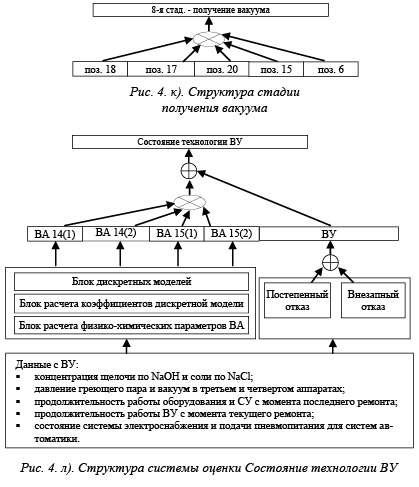
Если анализировать приведенную на рисунке 4 концептуальную модель, то можно отметить, что она позволяет использовать различный математический аппарат для оценки состояний элементов технологий, предварительно не оговаривая, какой именно. Определяющим фактором в данном случае является имеющаяся информация о свойствах ХТС. Используемые символы при построении данной модели (дизъюнкция и конъюнкция) Å и Ä могут являться аналогами различных алгебраических операций, которые применяются в алгебре Буля, в теории неопределенностей Заде, в использовании интервальных логических переменных, а также в теории вероятностей.
Необходимо отметить, что данная универсальность подхода открывает хорошие перспективы в исследовании технологической безопасности и в разработке системы диагностики состояний и управления.
Построение функций принадлежности лингвистических термов с использованием статистических данных
Описываемый далее метод построения функций принадлежности лингвистических термов основан на обработке статистических данных. В качестве степени принадлежности элемента множеству принимается оценка частоты использования понятия, задаваемого нечетким множеством, для характеристики элемента. Достаточно подробное описание различных методов построение функций принадлежности можно найти, например, в [7].
Краткие сведения о методе
При построении автоматизированных систем управления возникает задача моделирования деятельности человека-оператора. Один из путей ее решения – использование теории нечетких множеств на основе понятия функции принадлежности.
Функция принадлежности mА(u) ставит в соответствие каждому элементу uÎU число из интервала
[0, 1], характеризующее степень принадлежности элемента u множеству А. Человек, воспринимая информацию, не пользуется конкретными числами, а переводит их в свои понятия – значения лингвистической переменной. Каждое значение лингвистической переменной описывается функцией принадлежности, которая индивидуальна для каждого человека.
Предположим, что, наблюдая за объектом в течение некоторого времени, человек n раз фиксирует свое внимание на том, имеет место факт А или нет. Событие, заключающееся в n проверках наличия факта А, будем называть оценочным. Пусть в k проверках имел место факт А. Тогда оператор регистрирует частоту p = k/n появления факта А и оценивает ее с помощью слов типа «часто», «редко» и т.п.
Оценивая частоту p, оператор опирается на свой опыт, который отражает частоту появления факта А в событиях прошлого, представляющихся ему аналогичными оцениваемому событию. К нему поступает также информация, основанная на наблюдении других людей о появлении факта А, то есть информация, отражающая общественный опыт. В зависимости от степени доверия к источнику такого рода информации она запоминается с различными весами.
На универсальной шкале [0, 1] необходимо разместить значения лингвистической переменной: ВЕСЬМА РЕДКО, БОЛЕЕ-МЕНЕЕ РЕДКО, БОЛЕЕ-МЕНЕЕ ЧАСТО, ВЕСЬМА ЧАСТО. Тогда степень принадлежности некоторого значения вычисляется как отношение числа экспериментов, в которых оно встречалось в определенном интервале шкалы, к максимальному для этого значения числу экспериментов по всем интервалам. Метод основывается на условии, что в каждый интервал шкалы попадает одинаковое число экспериментов. Это условие часто не соблюдается. В реальных случаях составляется эмпирическая таблица, в которой эксперименты могут быть распределены неравномерно по интервалам, а в некоторые интервалы могут вообще не попасть.
Предположим, что специалисту в области химической технологии предлагают оценить по десятибалльной шкале значения лингвистической переменной Значения некоторого параметра. Термы лингвистической переменной при этом могут быть следующие: ПЛОХО, ХОРОШО, ОПАСНО, НОРМА, СРЕДНЕ, МНОГО, ОЧЕНЬ МНОГО и т.д. Термы выбираются экспертами в данной технологии в зависимости от значений каждого технологического параметра при условии, что они должны словесно описывать все возможные состояния значений этого параметра.
Далее разбиваем область существования параметра на точки с определенным шагом, шаг выбираем как минимальное изменение параметра, которое может, с точки зрения экспертов, оказать влияние на работу данного технологического процесса. В итоге для каждого параметра получаем ряд дискретных значений. Экспертам, в качестве которых выступают технорук, начальник цеха, начальники смен, предлагают сделать оценку значений параметров по десятибалльной шкале по каждому из заданных термов. В результате получаем таблицу следующего вида (табл. 3).

Далее вычисляем элементы матрицы подсказок . Выбираем в полученной строке максимальный элемент , и далее все элементы преобразуются по формуле
. (45)
Для столбцов, где kj=0, применяется линейная аппроксимация:
. (46)
Для построения функций принадлежности находим максимальные элементы по строкам таблицы, полученным после преобразования (1):
.
Функцию принадлежности вычисляем по формуле
.
В итоге получаем таблицу из m(cij), которая позволяет построить функции принадлежности для заданных термов технологических параметров (табл. 4).

Расчет функций принадлежности для технологических параметров МВУ
Концентрация NaОН на входе в первый ВА – B1in.
Интервал изменения параметра – [6.5; 11.5].
Шаг изменения – 0,5.
В таблице 5 представлены экспертные оценки для параметра B1in в заданном интервале bij, (i=1, 2; j = 1 …13).
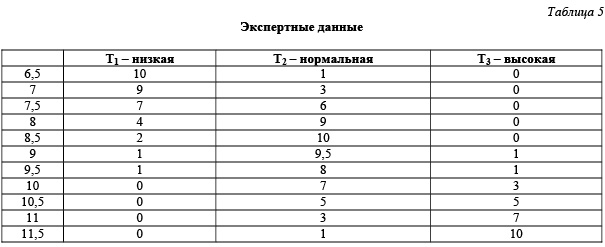
Вычислим элементы матрицы подсказок по формуле
.
Получим kj={12, 12, 13, 13, 12, 10,5, 10, 10, 10, 10, 11}. Находим kmax=13. Далее вычисляем cij и mij, по формулам:
.
Результаты представлены в таблице 6.
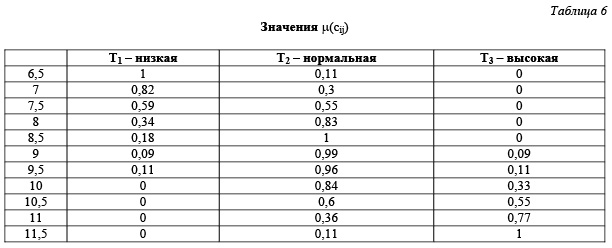
На основании полученных данных строим график функций принадлежности для термов (рис. 5).
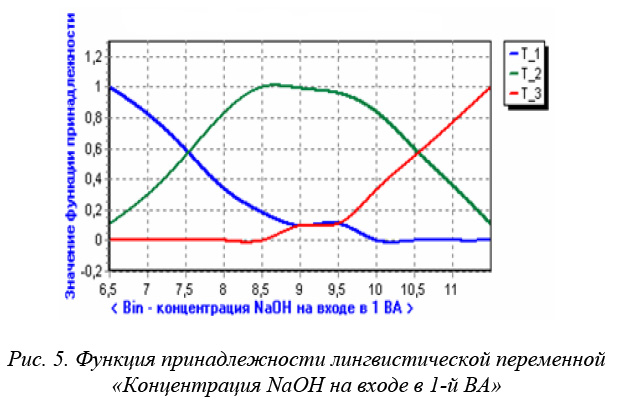
Определение центра безопасности для технологических параметров выпарных аппаратов цеха выпаривания
В соответствии с алгоритмом определения центра безопасности произведем вычисление центра
безопасности для технологических параметров выпарных аппаратов.
Расчет центра безопасности для технологических параметров первого ВА
1. Концентрация NaОН на входе в первый ВА – B1in.
Интервал изменения параметра – [6; 12] %. Множество интервалов значений параметра B1in:
X={X1; X2; X3; X4; X5; X6}={(6,5, 7,5); (7,5, 8,5); (8,5, 9,5); (9,5, 10,5); (10,5, 11,5); (11,5, 12,5)}.
Матрица нечеткого отношения предпочтения xRy – «интервал x значений параметра P1 не хуже
(с точки зрения безопасности функционирования технологического процесса) интервала y значений параметра P1» выглядит следующим образом:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
|
x1 |
1 |
0,2 |
0 |
0,1 |
0,5 |
0,7 |
|
x2 |
0,6 |
1 |
0,2 |
0,1 |
0,6 |
0,8 |
|
x3 |
1 |
0,7 |
1 |
0,8 |
0,9 |
1 |
|
x4 |
0,5 |
0,4 |
0,2 |
1 |
0,1 |
0 |
|
x5 |
0,6 |
0,5 |
0,1 |
0,7 |
1 |
0,3 |
|
x6 |
0,7 |
0,3 |
0,1 |
0,9 |
0,7 |
0,1 |
Матрица нечеткого отношения доминирования RD=R\R-1 с функцией принадлежности :
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
|
x1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
x2 |
0,4 |
0 |
0 |
0 |
0 |
0,1 |
|
x3 |
1 |
0,5 |
0 |
0,6 |
0,7 |
0,9 |
|
x4 |
0,4 |
0,3 |
0 |
0 |
0 |
0 |
|
x5 |
0,1 |
0 |
0 |
0,6 |
0 |
0 |
|
x6 |
0 |
0 |
0 |
0,9 |
0,4 |
0 |
Нечеткое подмножество недоминируемых альтернатив, согласно запишем в следующем виде:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
0 |
0,5 |
1 |
0,1 |
0,3 |
0,1 |
Найдем область центра технологической безопасности для параметра B1in. Для этого необходимо найти . Следовательно, так как , то X 3;º(8.5, 9.5) – область центра технологической безопасности для параметра B1in.
2. Концентрация NaОН на выходе из первого ВА – B1out.
Интервал изменения этого параметра – [9; 14] %. Множество интервалов значений параметра B1out: X={X1; X2; X 3; X4; X5}={(9, 10); (10, 11); ( 11, 12); (12, 13); (13, 14)}.
Матрица нечеткого отношения предпочтения x3Rxj:
|
X1 |
X2 |
X3 |
X4 |
X5 |
|
|
X1 |
1 |
0,2 |
0,3 |
0,2 |
0,2 |
|
X2 |
0,6 |
1 |
0,1 |
0,2 |
0,3 |
|
X3 |
1 |
0,8 |
1 |
0,8 |
0,9 |
|
X4 |
0,8 |
0,5 |
0,3 |
1 |
0,4 |
|
X5 |
0,6 |
0,3 |
0,1 |
0,5 |
1 |
Множество недоминируемых альтернатив:
|
X1 |
X2 |
X3 |
X4 |
X5 |
|
0 |
0,3 |
1 |
0,5 |
0,2 |
область центра технологической безопасности для параметра B1out.
3. Давление греющего пара на входе в первый ВА – P1in.
Интервал изменения этого параметра – [8; 12] Ат. Множество интервалов значений параметра P1in: X={X1; X2; X 3; X4}={(8, 9); (9, 10); (10, 11); (11, 12)}.
Матрица нечеткого отношения предпочтения xiRxj:
|
X1 |
X2 |
X3 |
X4 |
|
|
X1 |
1 |
0,2 |
0 |
0,2 |
|
X2 |
0,7 |
1 |
0,3 |
0,5 |
|
X3 |
1 |
0,8 |
1 |
0,8 |
|
X4 |
0,7 |
0,6 |
0,2 |
1 |
Множество недоминируемых альтернатив:
|
X1 |
X2 |
X3 |
X4 |
|
0 |
0,5 |
1 |
0,4 |
область центра технологической безопасности для параметра P1in.
4. Давление вторичного пара на выходе из первого ВА – P1out.
Интервал изменения этого параметра – [4; 7] Ат. Множество интервалов значений параметра P1out: X={x1; x2; x 3}={(4, 5); (5, 6); ( 6, 7)}.
Матрица нечеткого отношения предпочтения xiRxj:
|
X1 |
X2 |
X3 |
|
|
X1 |
1 |
0,1 |
0,6 |
|
X2 |
0,8 |
1 |
1 |
|
X3 |
0,3 |
0 |
1 |
Множество недоминируемых альтернатив:
|
X1 |
X2 |
X3 |
|
0,3 |
1 |
0 |
область центра технологической безопасности для параметра P1in.
5. Уровень раствора в греющей камере в первом ВА – H1.
Интервал изменения этого параметра – [0; 30], см. Множество интервалов значений параметра H1: X={x1; x2; x3 }={(0, 10); (10, 20); ( 20, 30)}.
Матрица нечеткого отношения предпочтения xiRxj:
|
X1 |
X2 |
X3 |
|
|
X1 |
1 |
0,2 |
0,6 |
|
X2 |
0,7 |
1 |
0,9 |
|
X3 |
0,2 |
0,1 |
1 |
Множество недоминируемых альтернатив:
|
X1 |
X2 |
X3 |
|
0,5 |
1 |
0,2 |
область центра технологической безопасности для параметра H1.
6. Расход вторичного пара на выходе из первого ВА – W1.
Интервал изменения этого параметра – [2; 5], см. Множество интервалов значений параметра W1: X={x1; x2; x3 }={(2, 3); (3, 4); ( 4, 5)}.
Матрица нечеткого отношения предпочтения xiRxj:
|
X1 |
X2 |
X3 |
|
|
X1 |
1 |
0 |
0,1 |
|
X2 |
1 |
1 |
0,3 |
|
X3 |
0,6 |
0,2 |
1 |
Множество недоминируемых альтернатив:
|
X1 |
X2 |
X3 |
|
0,5 |
1 |
0,9 |
область центра технологической безопасности для параметра W1.
7. Концентрация выпавшей в осадок соли на выходе из первого ВА – F1.
Интервал изменения этого параметра – [10; 14], см. Множество интервалов значений параметра F1: X={x1; x2; x3; x 4}={(10, 11); (11, 12); (12, 13); (13, 14)}.
Матрица нечеткого отношения предпочтения xiRxj:
|
X1 |
X2 |
X3 |
X4 |
|
|
X1 |
1 |
0,2 |
0,8 |
0,9 |
|
X2 |
0,6 |
1 |
0,8 |
1 |
|
X3 |
0 |
0,1 |
1 |
0,6 |
|
X4 |
0 |
0 |
0,2 |
1 |
Множество недоминируемых альтернатив:
|
X1 |
X2 |
X3 |
X4 |
|
0,6 |
1 |
0,2 |
0 |
область центра технологической безопасности для параметра F1.
Таким образом, в работе рассмотрено построение системы диагностики состояний и управления технологической безопасностью на примере технологических процессов выпаривания при производстве каустической соды, приводится математическое описание режимов работы выпарных аппаратов, проведено исследование индекса безопасности для технологических параметров, оборудования и систем управления.
Литература
1. Игнатьев М.В., Путилов В.А., Смольков Г.Я. Модели и системы управления комплексными экспериментальными исследованиями. М.: Наука, 1986. 232 с.
2. Богатиков В.Н. Исследование технологической надежности и оптимизация управления системой многокорпусных установок производства хлора и каустика: дис. … кан. техн. наук. М., МХТИ, 1978.
170 с.
3. Kasumasa H., Masataka I., Toshimitnu U. IEEETrans. Auto. Contr. 1981. AC-26, no. 2, pp. 601–603.
4. Корноушенко Е.К., Пылаев Н.К. Новый подход к диагностированию линейных диагностических систем // Автоматика и телемеханика. 1989. № 5. С. 148–159.
5. Алефельд Г., Херцбергер Ю. Введение в интервальные вычисления. М.: Мир, 1987. 360 с.
6. Пасманик М.И., Сасс-Тисовский Б.А., Якименко М.И. Производство хлора и каустической соды: справочник. М.: Химия, 1966. 308 с.
7. Борисов А.Н., Крумберг О.А., Федоров И.П. Принятие решений на основе нечетких моделей: Примеры использования. Рига: Зинатне, 1990. 184 с.
CONSTRUCTION OF THE EVALUATION SYSTEM OF STATES ON THE BASIS OF SAFETY INDEX ON EXAMPLE OF PRODUCTION CAUSTIC SODA EVAPORATION
Vent D.P. , Dr. Sc. (Engineering), Professor; Prorokov A.E., Ph.D. (Engineering), Associate Professor;
Sanaeva G.N. , Senior Lecturer
(Novomoskovsk Institute of MUCTR. D.I. Mendeleev, Druzhby st. 8, Tula Reg., Novomoskovsk,
301665, Russian Federation, k_vtit@dialog.nirhtu.ru);
Palyukh B.V. , Dr.Sc. (Engineering), Professor; Semenov N.A., Dr.Sc. (Engineering), Professor;
Bogatikov V.N. , Dr.Sc. (Engineering), Professor; Alekseev V.V., Ph.D. (Engineering), Associate Professor; Kemaykin V.K., Ph.D. (Engineering), Associate Professor
(Tver State Technical University, Nikitin Quay 22, Tver, 170026, Russian Federation, is@tstu.tver.ru)
Toichkin N.A. , Ph.D. (Engineering), Associate Professor, toichkin@list.ru
(Kola branch of Petrozavodsk state University, Lesnaya st. 29, Murmansk Reg., Apatity,
184209, Russian Federation)
Abstract. The paper considers the the construction of diagnostics system of the states and managing of technological safety for example, of evaporation of processes producing caustic soda. The paper considers the the four cabinet evaporation plant the production of chlorine and caustic soda. This technology is an example of a typical evaporation of process is constantly used in the production of chlorine and caustic soda. The paper presents statistical data, from the experience of operating the shop residue chlorine production Novomoskovsk.
Calculations to determine the center of the safety of the process evaporation and graphics terms of membership functions of linguistic variables, which determine to the technological parameters the degree of their location in the area of safety or hazardous conditions. A study for the safety index of technological parameters, equipment and management systems are discussed.
Keywords: technological safety, safety control, chemical-technological process (CTP), diagnostic system of states, safety center, safety degree, four cabinet evaporation plant the production of chlorine and caustic soda.
Comments