Современная СБИС может содержать десятки миллионов транзисторов, поэтому в связи с ограниченными возможностями вычислительных средств (память, скорость) не может быть спроектирована топология всей схемы в целом. Нормальным является разбиение схемы группированием компонентов в блоки. В результате разбиения формируется множество блоков и соединений между ними. В очень больших схемах используется иерархическая структура разбиения [1, 2].
Задачи разбиения можно разделить на два класса [3]:
– задачи, в которых осуществляется разбиение схемы на блоки с учетом конструктивных факторов, таких как размер блоков, число блоков и соединений между блоками, число внешних выводов у блоков
и т.д.;
– задачи, в которых, помимо конструктивных факторов, существенны и функциональные характеристики блоков.
В данной работе рассматривается метод решения наиболее распространенных задач первого класса.
Существующие алгоритмы разбиения делятся на два класса: конструктивные и итеративные [4, 5].
Входными данными для конструктивных алгоритмов являются компоненты и связи между ними, выходными – разбиение схемы на блоки, полученное, как правило, путем последовательного распределения компонентов по блокам. Алгоритмы этого класса отличаются, с одной стороны, относительным быстродействием, а с другой – низким качеством решений.
В качестве исходных данных итеративные алгоритмы дополнительно используют некоторое начальное разбиение схемы. На каждой итерации осуществляется переход к новому разбиению (решению).
Изменение разбиения осуществляется с помощью групповых или парных перестановок между блоками. Суть итерационного алгоритма – поиск в пространстве решений решения (разбиения) с лучшими показателями качества. Отметим, что в качестве начального разбиения итеративный алгоритм может использовать либо случайное разбиение, либо разбиение, полученное в результате работы конструктивного алгоритма.
В свою очередь, итеративные алгоритмы делятся на детерминированные и вероятностные [3, 4].
В детерминированных алгоритмах изменение разбиения (решения) реализуется на основе четкой
детерминированной зависимости от изменяемого решения. Недостатком является частое попадание в локальный оптимум (локальную яму).
В вероятностных алгоритмах переход к новому решению осуществляется случайным образом. Недостатком алгоритмов, реализующих чисто случайный поиск, является значительная трудоемкость.
Дальнейшим совершенствованием алгоритмов случайного поиска является разработка методов, основанных на моделировании естественных процессов. К ним относятся методы моделирования отжига, метод эволюционного моделирования, генетической адаптации, биоинспирированные алгоритмы [6–11].
Все эти методы относятся к классу методов случайного направленного поиска и имеют существенные отличия. К недостаткам относится то, что они все же в большей степени реализуют стратегии «слепого» поиска, что увеличивает объем просматриваемого пространства решений.
Особый интерес представляет поисковая адаптация, основанная на использовании обучающихся автоматов, моделирующих поведение объекта адаптации в среде. Трудности использования такого подхода связаны прежде всего с проблемой представления исходной формулировки задачи в виде адаптивной системы. Достоинствами являются повышенная целенаправленность и сходимость алгоритма [12].
В работе используется представление задачи разбиения в виде адаптивной системы, основными компонентами которой являются среда (объект оптимизации) и вероятностный автомат, помещенный в эту среду и реализующий алгоритм поиска [12, 13].
Постановка задачи разбиения
Большинство разработанных к настоящему времени алгоритмов разбиения используют в качестве модели схемы граф или гиперграф [1, 2]. Существенным недостатком при использовании графа в качестве модели схемы является наличие неоднозначности, так как одной цепи соответствует набор деревьев, построенных на связываемых этой цепью вершинах.
Задача разбиения гиперграфа с взвешенными вершинами и ребрами формулируется следующим образом.
Дан гиперграф H = (X, E), где X = {xi | i=1, 2, …,n} – множество вершин, а ![]() – множество ребер (каждое ребро – подмножество связываемых им вершин). Вес вершин задается множеством
– множество ребер (каждое ребро – подмножество связываемых им вершин). Вес вершин задается множеством ![]() 1, 2, …,n}, а вес ребер – множеством
1, 2, …,n}, а вес ребер – множеством ![]() 1, 2, …,n}. Необходимо сформировать К узлов, то есть множество X разбить на К непустых и непересекающихся подмножеств
1, 2, …,n}. Необходимо сформировать К узлов, то есть множество X разбить на К непустых и непересекающихся подмножеств ![]() (рис. 1). На формируемые узлы накладываются ограничения. С помощью вектора P = {pv | v=1, 2, …,k} задается максимально допустимый суммарный вес вершин, назначенных в v-й узел, а с помощью вектора N ={nv | v=1, 2, …,k} – максимально допустимое число вершин, назначенных в v-й узел.
(рис. 1). На формируемые узлы накладываются ограничения. С помощью вектора P = {pv | v=1, 2, …,k} задается максимально допустимый суммарный вес вершин, назначенных в v-й узел, а с помощью вектора N ={nv | v=1, 2, …,k} – максимально допустимое число вершин, назначенных в v-й узел.
Ограничения на вместимость имеют вид:
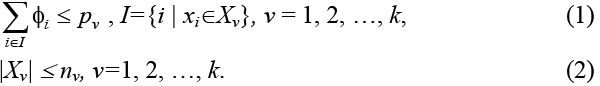
Выражение (1) является ограничением на максимальный вес узла, а выражение (2) – на максимальное число вершин в узле.
Иногда задано допустимое число выводов ![]() max для узлов. Ограничение для узлов на число выводов
max для узлов. Ограничение для узлов на число выводов ![]() v имеет вид:
v имеет вид:
![]() (3)
(3)
Ev – множество ребер, связывающих множество вершин Xv с вершинами остальных узлов.
Основным критерием является F1 – суммарная стоимость ребер в разрезе.
![]() (4)
(4)
![]() – множество ребер в разрезе.
– множество ребер в разрезе.
Вторым часто используемым критерием является F2 – суммарное число выводов.
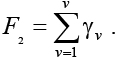 (5)
(5)
Возможно использование критерия F, являющегося аддитивной сверткой критериев F1 и F2:
F = k 1 × F 1 + k 2 × F 2.
Задачу разбиения гиперграфа H = (X, E) со взвешенными вершинами и ребрами сведем к задаче о назначении множества гиперребер Е в К узлов при выполнении следующих условий: каждое гиперребро может быть назначено только в один узел, а стоимость вершин, назначенных в узел zv, не должна превышать наперед заданную величину pv. Будем считать, что гиперребро ej назначено в узел zv, если все множество составляющих его вершин назначено в этот узел.
Введем булевы переменные:


Согласно описанным условиям, должны выполняться следующие ограничения:
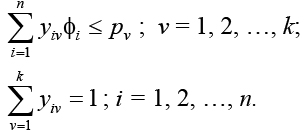
Цель оптимизации – минимизация стоимости связей между узлами, или, что одно и то же, максимизация стоимости гиперребер, полностью размещенных в узлах. Целевая функция примет вид:
максимизировать
![]()
Установим связь между переменными hjv и yiv с помощью следующей группы ограничений:
![]()
где ![]() – мощность множества ej, то есть
– мощность множества ej, то есть ![]() .
.
Действительно, при некотором опорном плане, то есть пробном назначении гиперребер в узлы, в соответствии с этой группой ограничений все составляющие эти ребра вершины будут также назначены в те же узлы. Таким образом, задача разбиения гиперграфа со взвешенными вершинами и ребрами по критерию минимальной стоимости связей между узлами формулируется следующим образом:
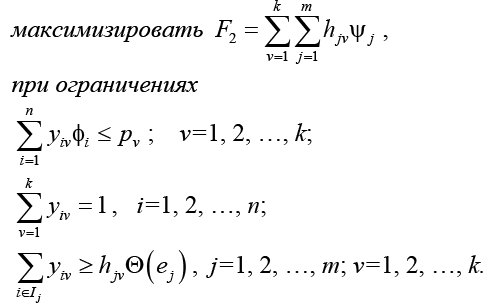
Число ограничений D = (m + 1) × k + n.
Для построения математической модели задачи разбиения гиперграфа с взвешенными вершинами и ребрами по критерию минимума числа выводов формируемых узлов введем булеву переменную qjv:
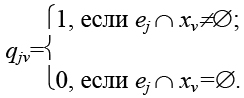
Целью задачи является отыскание минимума функции
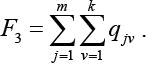
Установим связь между переменными qjv и yiv с помощью следующей группы ограничений:
![]()
где ![]() – мощность множества ej, то есть
– мощность множества ej, то есть ![]() .
.
Действительно, при некотором опорном плане в соответствии с этой группой ограничений qjv = 0 только в том случае, когда ни одна из вершин, входящих в состав гиперребра ej, не назначена в узел zv.
Задача разбиения гиперграфа с взвешенными вершинами и ребрами по критерию минимума числа выводов формируемых узлов формулируется следующим образом:
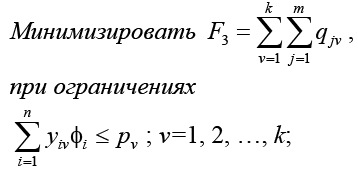
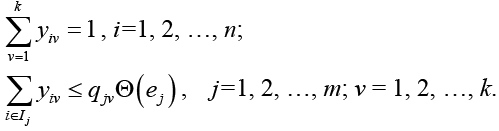
Число ограничений D = (m + 1) × k + n.
Механизмы кооперативного поведения агентов для решения задачи разбиения
Исходная формулировка задачи представляется в виде адаптивной многоагентной системы, работа которой основана на идеях коллективного поведения объектов адаптации.
В качестве агента (элементарного объекта адаптации) рассматривается вершина ![]() Коллектив агентов (их совокупность) соответствует объекту оптимизации (ОО). Кооперативное поведение агентов для решения общей задачи предполагает согласование действий в процессе решения задачи.
Коллектив агентов (их совокупность) соответствует объекту оптимизации (ОО). Кооперативное поведение агентов для решения общей задачи предполагает согласование действий в процессе решения задачи.
Работу адаптивной многоагентной системы можно представить как функционирование некоторого роя вероятностных автоматов адаптации (АА), действующего в случайной среде функционирования [13, 14]. Под средой функционирования понимается объект управления (ОО). Функции управляющего устройства агента xi реализуются АА ai, состояние которого Аi изменяется в соответствии с откликом среды функционирования Q.
В рассматриваемом случае в качестве ОО (среды функционирования) рассматривается гиперграф, разбитый на К узлов. Состояние среды функционирования оценивается вектором S = {si | i = 1, 2, …, n}, где si – номер узла, в который помещена вершина xi. В основе работы адаптивной многоагентной системы лежит ситуационная кооперация между агентами, когда решение о совместных действиях принимается агентами на каждом такте работы на основе анализа состояния S среды функционирования и наличия у агентов условий для кооперации. Компонента управления (АА ai) агентом xi определяет элементарные действия агента для различных состояний среды функционирования.
На каждом такте работы адаптивной многоагентной системы в соответствии с состояниями А роя автоматов адаптации (РАА) формируется управляющее воздействие U, приводящее к изменению состояния S среды функционирования и показателя F(S) (рис. 2).
Q является откликом среды на реализацию управляющего воздействия U . Под действием Q автоматы переходят в новое состояние и вырабатывают новые значения А.
Пусть P={Si | i = 1, 2, …} – пространство возможных состояний среды функционирования (возможных решений задачи разбиения).
Предлагаемый алгоритм разбиения является алгоритмом случайного поиска в пространстве состояний – Р. Алгоритм случайного поиска представляется в виде коллектива вероятностных автоматов, адаптация которых производится путем введения самообучения в процессе их функционирования [14].
Пусть объект оптимизации (среда функционирования) находится в некотором состоянии Sj, то есть заданы разбиение Х и, соответственно, распределение вершин xi по узлам.
Пусть pi+ – число гиперребер, связывающих ![]() с вершинами
с вершинами ![]() – число гиперребер, связывающих
– число гиперребер, связывающих ![]() с вершинами
с вершинами ![]() – локальная степень вершины xi.
– локальная степень вершины xi.
Локальная цель агента (объекта адаптации x i) – достижение такого состояния (то есть такого распределения xi), при котором его оценка ![]() = 0. Другими словами, в процессе адаптации минимизируется
= 0. Другими словами, в процессе адаптации минимизируется ![]() .
.
Глобальная цель многоагентной системы (коллектива объектов адаптации) заключается в достижении такого состояния S (то есть такого распределения вершин по узлам), при котором ![]()
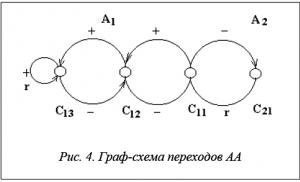
Для реализации механизма адаптации каждому агенту xi Î X сопоставляется АА ai, моделирующий поведение объекта адаптации в среде функционирования [14]. АА имеет две группы состояний: C 1 = {c1i | i = 1, 2, …, g} и C2={c21}, соответствующие альтернативам А1 и А2 поведения агента в среде функционирования. А1 – остаться в том же узле, А 2 – выход из узла и перераспределение. Таким образом, выходной алфавит автомата – А = {А1, А2}. Входной алфавит – Q = {+, –} включает возможные отклики среды функционирования – «поощрение» (+) и «наказание» (–).
Граф-схема переходов АА показана на рисунке 4.
Отклик среды для АА ai в соответствии с состоянием среды и объекта адаптации формируется следующим образом.
Если ![]() , то всегда вырабатывается сигнал «наказание» (–).
, то всегда вырабатывается сигнал «наказание» (–).
Если ![]() , то с вероятностью
, то с вероятностью ![]() вырабатывается сигнал «наказание» (–); а с вероятностью вырабатывается сигнал «поощрение» (+).
вырабатывается сигнал «наказание» (–); а с вероятностью вырабатывается сигнал «поощрение» (+).
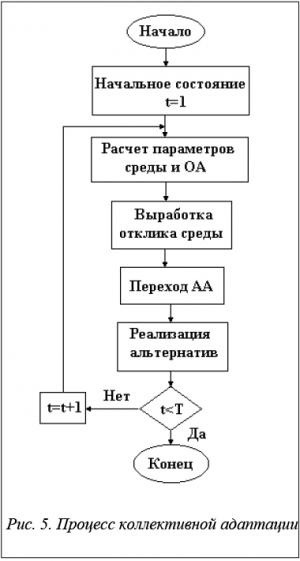
На каждой итерации работы адаптивной системы процесс коллективной адаптации осуществляется за четыре такта (рис. 5).
На первом такте в соответствии с состоянием среды для каждого объекта адаптации рассчитываются параметры 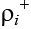 и
и ![]() .
.
На втором такте для каждого автомата адаптации ai = Г( xi) вырабатывается отклик среды qi: сигнал «поощрение» (+) или «наказание» (–).
На третьем такте в каждом автомате адаптации ai под действием подаваемого на его вход отклика qi осуществляется переход в новое состояние.
На четвертом такте реализуется альтернатива в соответствии с выходами АА. Объект оптимизации после реализации альтернатив переходит в новое состояние, для которого рассчитывается показатель F(S) . Состояние с лучшим значением F(S) запоминается.
Рассмотрим процесс реализации для объектов адаптации альтернативы А 2 – выход из узла и перераспределение.
Из всех подмножеств Xv удаляются вершины xi, для которых реализуется альтернатива А2. Все такие вершины объединяются в множество R = {Rv |v = 1, 2, …, k}, гдеRv – множество вершин, удаленных из Xv.
Процесс переназначения вершин осуществляется последовательно. На каждом шаге случайным образом (равновероятно) выбирается вершина ![]() . Для нее определяется множество доступных узлов. Узел Xv является доступным, если после назначения в него xi допустимый вес pv или допустимое число вершин nv не будут перекрыты.
. Для нее определяется множество доступных узлов. Узел Xv является доступным, если после назначения в него xi допустимый вес pv или допустимое число вершин nv не будут перекрыты.
Обозначим через riv число гиперребер, связывающих выбранную xi с доступным узлом Xv.
![]() – число связей xi c доступными узлами.
– число связей xi c доступными узлами.
Пусть w – число доступных узлов.
Назначение xi в один из доступных узлов осуществляется вероятностным способом.
Вероятность назначения xi в недоступный узел равна нулю.
Вероятность попадания xi в один из доступных узлов Xv пропорциональна числу связей xi с Xv и определяется как
![]()
где Pi – распределение вероятности назначения для xi; Pi – рассчитывается только для выбранной для переназначения xi. С помощью параметра d осуществляется управление распределением вероятностей для xi.
В работе используется подход, имеющий сходство с методом моделирования отжига.
Параметр ![]() вычисляется по формуле
вычисляется по формуле
![]() – номер итерации.
– номер итерации.
![]()
где ![]() – управляющие параметры, задаваемые заранее (выбираемые из эвристических соображений).
– управляющие параметры, задаваемые заранее (выбираемые из эвристических соображений). 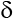 имеет максимальное значение на первой итерации работы адаптивной системы. Последовательно уменьшаясь,
имеет максимальное значение на первой итерации работы адаптивной системы. Последовательно уменьшаясь, ![]() приобретает минимальное значение на итерации Т0 и после этого не меняется. В процессе переназначения множества R на итерации t параметр
приобретает минимальное значение на итерации Т0 и после этого не меняется. В процессе переназначения множества R на итерации t параметр 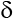 не меняется. Чем больше
не меняется. Чем больше 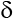 , тем более близким (равновероятным) становятся значения
, тем более близким (равновероятным) становятся значения ![]() . Другими словами, на первых итерациях переназначаемые элементы имеют большую степень свободы и меньшую степень зависимости от piv и поэтому элемент xi может попасть в узел, с которым он не связан. После выполнения T итераций, если при переназначении xi имеет связи с доступными узлами, то вероятность попадания xi в доступный узел, с которым нет связей, близка к нулю.
. Другими словами, на первых итерациях переназначаемые элементы имеют большую степень свободы и меньшую степень зависимости от piv и поэтому элемент xi может попасть в узел, с которым он не связан. После выполнения T итераций, если при переназначении xi имеет связи с доступными узлами, то вероятность попадания xi в доступный узел, с которым нет связей, близка к нулю.
Отметим, что 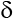 не может быть равной нулю (а следовательно, и a0 ), ибо возможна ситуация в процессе переназначения R, когда будет выбрана такая вершина xi, что для всех доступных узлов
не может быть равной нулю (а следовательно, и a0 ), ибо возможна ситуация в процессе переназначения R, когда будет выбрана такая вершина xi, что для всех доступных узлов ![]() .
.
Такой подход к расчету распределения вероятности назначения вершины создает условия для выхода из локальных оптимумов.
На рисунке 6 представлен псевдокод адаптивного алгоритма разбиения.
Процедурой ИСХОД_ДАННЫЕ формируется массив граф, в котором хранятся исходные данные, описывающие задачу. Массив управление, сформированный процедурой НАСТРОЙКА, хранит значения управляющих параметров: число итераций, число набросов, ![]() , g – глубина памяти АА и т.п.
, g – глубина памяти АА и т.п.
Процедурой ИСХОД_РАЗБИЕНИЕ(граф) формируется случайным образом начальное состояние среды S, то есть начальное разбиение гиперграфа – решение. Это решение на данный момент считается лучшим и заносится в массив лучш_решение.
С помощью процедуры НАЧ_СОСТОЯНИЕ все АА переводятся в состояние Cn. Состояние АА заносится в массив состоян_аа . Затем выполняется заданное число итераций. С помощью процедурыРАСЧЕТ(решение) рассчитываются параметры ![]() и
и ![]() объектов адаптации, которые заносятся в массив параметры_оа.
объектов адаптации, которые заносятся в массив параметры_оа.
Процедурой РЕАКЦИЯ(параметры_оа) формируется массивотклик со значениями откликов среды для каждого автомата адаптации ai.
Процедурой ПЕРЕХОД(состоян_аа, отклик) автоматы адаптации переходят в новые состояния, которые фиксируются в массиве состоян_аа.
Затем процедурой ВЫХОД(граф, состоян_аа) формируется массив вершины, в который включаются вершины, для которых реализуется альтернатива А2.
Процедурой УДАЛИТЬ(решение, вершина) полное решение задачи заменяется частичным путем удаления из узлов Xv перераспределяемых вершин R.
После этого выполняется этап переназначения множества вершин R.
Процедурой ВЫБОР_ВЕРШ(вершины) выбирается случайным образомвершина. Для выбранной вершины процедурой ВЕРОЯТНО(вершина, решение, управление) формируется массив распределения вероятности переназначения – распределение.
Процедура ВЫБОР_УЗЛА(вершина, распределение) выбирает узел для назначения вершины.
Процедурой ДОБАВИТЬ(решение, вершина, узел) частичное решение уточняется путем размещения выбранной вершины в выбранный узел. После назначения всех вершин множества R массив решение вновь будет хранить полное решение задачи разбиения.
Если полученное решение имеет лучшую оценку F(S), то процедурой СРАВНЕНИЕ(решение, лучш_решение), оно заносится в массив лучш_решение.
Отметим, что 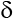 не может быть равной нулю (а следовательно, и a0 ), ибо возможна ситуация, когда для некоторой
не может быть равной нулю (а следовательно, и a0 ), ибо возможна ситуация, когда для некоторой ![]() при выборе узла окажется, что для всех доступных узлов значения
при выборе узла окажется, что для всех доступных узлов значения ![]() , а отсюда вытекает неопределенность значения piv.
, а отсюда вытекает неопределенность значения piv.
Экспериментальные исследования
При создании программы использовался пакет Visual Studio 2005 для 32-разрядных ОС семейства Windows 9x, а отладка, тестирование и эксперименты поводились на IBM
9x, а отладка, тестирование и эксперименты поводились на IBM совместимом компьютере с процессором AMD Athlon-64
совместимом компьютере с процессором AMD Athlon-64 3000+ и оперативной памятью 512 MB DIMM PC-3200.
3000+ и оперативной памятью 512 MB DIMM PC-3200.
Для проведения экспериментов была использована процедура синтеза контрольных примеров с известным оптимумом Fопт по аналогии с известным методом BEKU (Partitioning Examples with Tight Upper Bound of Optimal Solution) [15].
Исследованию подвергались примеры, содержащие до 1 000 вершин. Эксперименты показали, что временная сложность алгоритма на одной итерации имеет оценку О(n), где n – число вершин в гиперграфе.
Наилучшие результаты адаптивный алгоритм показал при следующих значениях управляющих параметров: g (глубина памяти) – 2; Т (число итераций) – 300; ![]()
Тестирование производилось на бенчмарках 19s, PrimGA1, PrimGA2. По сравнению с существующими алгоритмами достигнуто улучшение результатов на 5–9 %.
В среднем запуск программы со случайными начальными разбиениями обеспечивает нахождение решения, отличающегося от оптимального менее чем на 0,05 %, пяти запусков программы со случайными начальными разбиениями было достаточно для нахождения глобального оптимума.
Работа выполнена при финансовой поддержке гранта РФФИ № 17 - 07 – 00997.
Литература
1. Немудров В., Мартин Г. Системы-на-кристалле. Проектирование и развитие. М.: Техносфера, 2004. 216 с.
2. Малышев И.В., Немудров В.Г. Состояние и перспективы отечественных разработок СБИС типа «система на кристалле» // Системы и средства связи, телевидения и радиовещания. 2003. № 1, 2.
С. 56–57.
3. Норенков И.П. Основы автоматизированного проектирования. М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. 446 с.
4. Деньдобренко Б.П., Малика А.С. Автоматизация проектирования радиоэлектронной аппаратуры. М.: Высш. шк., 2002. 384 с.
5. Mehta D., Sapatnekar S., Alpert C. Handbook of Algorithms for Physical Design Automation. NY, CRC Press, 2009, 1042 р.
6. Chatterjee A. and Hartley R. A new simultaneous circuit partitioning and chip placemant approach based on simulated annealing. Proc. of Design Automation Conf., 1990, рр. 36–39.
7. Анализ и исследование эволюционных методов решения задач разбиения СБИС; [под ред. В.В. Курейчика]. Таганрог: Изд-во ТТИ ЮФУ, 2010. 84 с.
8. Лебедев Б.К., Лебедев О.Б. Разбиение на основе поисковой адаптации // Интеллектуальные системы. Коллективная монография; [под ред. В.М. Курейчика]. М.: Физматлит, 2005. С. 234–256.
9. Alpert C. and Kahng A. A hybrid multilevel/genetic approach for circuit partitioning. Proc. 5th ACM/SIGDA Physical Design Workshop, 2002, pр. 100–105.
10. Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой. М.: Изд-во МГТУ им. Н.Э. Баумана, 2014. 448 с.
11. Лебедев О.Б. Модели адаптивного поведения муравьиной колонии в задачах проектирования. Таганрог: Изд-во ЮФУ, 2013. 199 с.
12. Курейчик В.М., Лебедев Б.К., Лебедев О.Б. Поисковая адаптация: теория и практика.
М.: Физматлит, 2006. 272 с.
13. Цетлин М.Л. Исследования по теории автоматов и моделированию биологических систем. М.: Наука, 1969. 316 с.
14. Лебедев Б.К. Адаптация в САПР. Таганрог: Изд-во ТРТУ, 1999. 160 с.
15. Cong J., Romesis M., and Xie M. Optimality, scalability and stability study of partitioning and placement algorithms. Proc. Intern. Sympos. Physical Design, Monterey, CA. April 2003, pp. 88–94.

Comments