Multi-criteria decision analysis (MCDA) designed to select "optimal" / compromise solutions (alternatives), their ranking, selection or sorting [1–3]. MCDA is an effective tool for decision support for the selection of reasonable options for action [4–6].
In this paper, a Fuzzy MCDA model (FMCDA) refers to a fuzzy extension of an original (classical) MCDA method with the selected implementation of functions of fuzzy numbers (FNs) and a given method for ranking of FNs.
Presently, there are various FMCDA models, including fuzzy extensions of such well-known MCDA methods as TOPSIS, PROMETHEE, and AHP [7, 8].
In this paper, we present a Decerns-FT system that implements a fuzzy extension of the classical TOPSIS method [9]. The first Fuzzy TOPSIS (FTOPSIS) model was created in 1992 [10]. Later, based on the classical TOPSIS method, various FTOPSIS models were developed [7, 11].
At the moment, there are commercial and academic Computer Decision Support Systems (DSSs) that implement MCDA methods. The review [3] considers 47 DSSs implementing such MCDA methods as AHP, ELECTRE, MAVT, MAUT, PROMETHEE, TOPSIS, etc., including DSSs for group decision making [12]. We can also mention the academic system [13], which includes the FMCDA methods FuzzyVIKOR and FuzzyTOPSIS, for which 8 methods of FNs defuzzification are implemented [14]. This system is developed using PHP, MySQL, Ajax, and jQuery. FMCDA models in this system work with triangular and trapezoidal FN, linguistic variables, and group decision analysis are also supported.
At the same time, among the FMCDA models implemented in these systems, including the FTOPSIS models [11], none of the models uses different approaches to estimating functions of FNs and, accordingly, does not investigate the overestimation problem [15], including the problem of implementing dependent FNs in FMCDA models [16–18].
The need to implement and study the FTOPSIS models presented in [17] led to the development of the FuzzyLib library and the Decerns-FT FMCDA system. Exploring the influence of approaches to assessing functions of FNs method and fuzzy ranking methods on the output results (ranks of alternatives) led to the development of a module that allows implementing Monte Carlo methods to get statistical estimates of distinctions for multi-criteria choice (only one, as a rule, "best" alternative is chosen) and ranking [2] (alternatives are ranked from "best" to "worst") problems when using different models of FMCDA.
Fuzzy numbers and methods for ranking of fuzzy numbers
The fuzzy set [19] extends the concept of a classical set, in which the membership function can take values
in the segment (closed interval) [0, 1].
One of the key concepts in fuzzy set theory is the concept of an α- cut (alpha-cut).
For these methods, ranking of FNs is performed in the following way: the higher the defuzzified value, the higher the rank. The ranking of real numbers is implemented using one of the sorting algorithms. The developed system uses a quick sort algorithm.
2. Ranking methods based on estimating the distance to the reference fuzzy set. In these methods, a reference fuzzy set is defined, and for each FN from a given set of FNs, the distance to the reference set is calculated based on the used method. The definition of the reference set is often based on the FNs under consideration [14, 24]. Ranking methods of this class are not used in this paper.
3. Ranking methods based on the pairwise comparison. The ordering of a finite set of FNs, in this case, is based on their pairwise comparison. This class is represented by the largest number of FNs ranking methods [27, 30].
In this paper, we use one of the methods for ranking of FNs from this class, based on the Yuan's fuzzy preference relation (Y) [26, 27], which is effectively implemented using alpha-cuts of FN. The Yuan’s FPR can be summarized as follows in the form implemented within our research and developments [16–18].
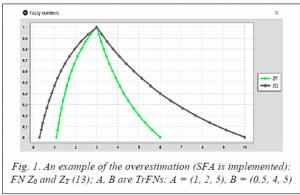
The overestimation problem arises when there are dependent variables in the fuzzy expression under consideration [15,18]: in (13) for the case ofZ0, the dependent variables are the numerator,A + B, and the denominator, A. At the same time, f1 and f2 (13) are equivalent, so the estimates of Z0 and ZT based on the extension principle (the proper estimate of the function of FNs) are also equivalent and, in the cases under consideration, coincide withZT. We add also that the use of TM to assess Z 0, as well as the use of SFA to calculate ZT , leads to the proper evaluation of these expressions.
To overcome the problem of dependent variables when calculating the proper result of a function f (Z 1, …,Zn), as well as to calculate the output value for non-monotonic real functions f(x 1, …,xn), transformation methods (TMs) can be used, which are one of the variants of interval computing on α-cuts. TMs are described in detail in [15].
Despite some approximation, we will call the output value Z, obtained based on a correct application of TM, the proper value for the function of FNs.
According to the algorithms RTM and GTM, the amount of the operations when calculating FN Z = f (Z1, …, Zn) and, consequently, running time of algorithms can be represented as O(Na kn), where is the maximum number of points used in a-cuts, Na is the number of a-cuts; within RTM, k = 2. To significantly reduce the computing time for implementing FMCDA models, including one within the Decerns - FT system, the process of parallel calculations is implemented.
FTOPSIS models
This section describes various models of FTOPSIS as a fuzzy extension of the classical TOPSIS method.
The FTOPSIS model implies the implementation of the following basic steps [17,18].
Depending on the methods used for estimating functions of FNs and ranking FNs, the following models can be used.
FTTr model (Fuzzy TOPSIS with Triangular Fuzzy Numbers, TrFNs), where approximate calculations are used to get a generalized criterionDi and the difference Dij = Di – Dj. The FTS (Fuzzy TOPSIS with Standard Fuzzy Arithmetic) model, where standard fuzzy arithmetic is used to get the generalized criterion Di and the difference Dij = Di – Dj. The FTR model (Fuzzy TOPSIS with Reduced Transformation Method, RTM), where RTM is used to assess generalized criterion (expression (22)) and the difference Dij = Di – Dj.
Depending on the used ranking method, there are the FTTrCI and FTTrIM models, where the CI and IM methods are used to rank alternatives, respectively; the FTSCI, FTSIM, FTRCI, FTRIM models, and the FTRY model, where the Yuan’s (Y) ranking method is used. It is worth noting that the implementation of the FTRY model, because of the use of TM for calculations requires much more time in comparison with other models.
Computer System Decerns-FT
This section describes the structure of Decerns-FT system, and the application of the system to investigate the distinctions of FTOPSIS models described in earlier.
The structure of Decerns-FT
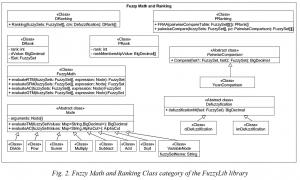
To implement FTOPSIS fuzzy models used in the Decerns-FT system, and the module for comparing fuzzy models based on Monte Carlo simulation, the FuzzyLib library was developed. It implements the library in the Java programming language. Figures 2 and 3 show the UML class diagram of the developed FuzzyLib library.
The "Fuzzy Math and Ranking" category includes classes that implement the process of calculating functions of FNs and FNs ranking.
1. The PRanking and DRanking classes implement ranking methods based on pairwise comparisons and defuzzification, respectively. The PRankingclass includes the pairwiseCompare method, which is designed for pairwise comparison of FNs. As arguments, it takes an array of fuzzy numbers fuzzySets and an object of the PairwiseComparison class, which implements the comparison of a pair of FNs. The FRAA method [16] implements the FRAA procedure for ranking a set of FNs based on the pairwiseCompareTable, which outputs an array
of generated objects of the PRank class. The object of the PRank class contains a field denoting the rank defined by the FRAA method and the FRAI rankmembershipvalue array. The DRanking class includes a ranking method designed to rank of FN fuzzySets based on the defuzzification method of the Defuzzification class object (dm argument). The output is an array of objects of the DRank class, which contains the rank number, the value of the dValue defuzzification method, and FN of fSet.
2. The fuzzymath class. This class implements methods for evaluating functions of FNs. As input arguments, it takes an expression built based on objects of the Node class in the tree type.
Each descendant of the Node class implements the evaluateTM and evaluateAC methods to calculate the input values individually (which is required in the RTM and GTM methods) or alpha-cuts as a whole (approximate calculation methods and standard fuzzy arithmetic). Objects of the VariableNode class using fuzzySetName allow to get an alpha-cut or the FN value considered by the transformation method from the fuzzySetValues argument.
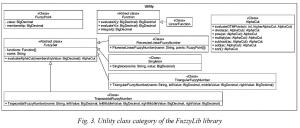
The Utility category includes classes describing the FNs (FuzzySet and its descendants), a mathematical function class (this class is required for obtaining alpha-cuts of a FN and evaluating integrals in the CI, IM, and Y (Yuan’s) ranking methods, and some other classes (for example, the AlphaCut class, which includes a method for determining auxiliary points in the GTM method and methods for evaluating basic mathematical operations, including addition, subtraction, division, multiplication, etc., using approximate calculations and standard fuzzy arithmetic).
The conceptual scheme of the Decerns-FT system, and the main modules of the FuzzyLib library, are presented in Figures 4 and 5, respectively.
The graphical interface of Decerns-FT includes modules for implementing the next steps in solving an FMCDA problem [17].
1. The value tree formation [33].
2. In the feature table, fuzzy values of criteria for the considered alternatives are set; the types of FNs membership functions used in Decerns-FT are shown in Figure 6, respectively: singletons, triangular, trapezoidal, piecewise linear (continuous, upper continuous), Gaussian, piecewise linear upper semi-continuous, bell-shaped, and FNs with sigmoid membership functions.
3. Setting fuzzy weight coefficients using the FSwing method [31] or the direct waiting method. Figure 7 shows an example of setting weights using FSwing.
4. Applying FTOPSIS models to solve a multi-criteria problem. The Decerns-FT system includes fuzzy models described in Section 3, see also Figure 4.
The adapted version of the desktop Decerns-FT system is also a subsystem of the modified and extended version of the DecernsMCDA [33, 34], which includes the following classical MCDA methods: MAVT, TOPSIS, AHP, PROMETHEE, MAUT, ProMAA, and FlowSort.
Comparison of FTOPSIS models using the Monte Carlo simulation
Consider the module for comparing FTOPSIS models implemented in Decerns-FT using Monte Carlo algorithms. The comparison is made by the number of distinctions in ranks of alternatives formed based on Monte Carlo simulation within the generated scenarios of fuzzy multi-criteria problems.
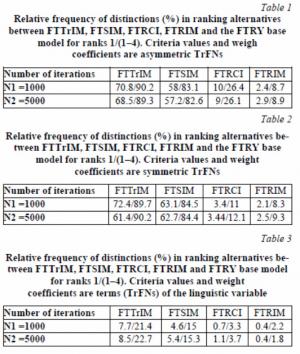
In this paper, there is a comparison of the ranks of alternatives according to FTRY model with the ranks by FTTrIM, FTSIM, FTRCI, and FTRIM models, Tables 1–3.
The paper considers the FMCDA problems with m = 4 criteria n = 4 alternatives. Based on Monte Carlo algorithms, 5000 iterations are generated, each of which generates a multi-criteria problem scenario. At the same time, we study both the multi-criteria choice problem (only the rank r1 = 1 is considered) and the ranking problem (all ranks r2 = {1, …, 4} are taken into account). Within the scenario, using TrFNs in the segment [0, 1], a performance table is generated (the values of alternatives according to criteria) along with weight coefficients using a uniform distribution in [0, 1].In this paper, three variants of TrFNs are generated: symmetric TrFNs (v = 1), general/non-symmetric TrFNs (v = 2), and terms of the linguistic variable (based on the seven-term scale of TrFNs in [0, 1]) (v = 3) [23]. For each scenario (t = 1, …, Nmax = 5000) and variant/form of TrFNs (v = 1, 2, 3) and for the specified fuzzy model Mk, the ranks of alternatives were evaluated and compared with the ranks of the basic model M0 (FTRY).Number of distinctions, D(t + 1; Mk, rl, v), t = 0, 1, …, Nmax – 1; k = 1, …, 4; l = 1, 2; v = 1, 2, 3, at each iteration for the compared pair increased by one if a distinction was found in at least one of the ranks of the sets r1 or, respectively, r2:D(t + 1; Mk, rl, v) +1, if there was no distinction in rank at iteration t + 1, then D(t + 1; Mk,rl, v) = D(t; Mk, rl, v). The frequency of distinctions in the ranks of alternatives when using different FTOPSIS methods (statistical assessment of the probability of distinction) was defined as p = D(Nmax;Mk, rl, v)/N max; D (0; Mk, rl, v) = 0. Note that estimates of distinctions were also made for the intermediate number of iterations Nmax = 1000; the latter indicates the level of distinctions in the ranks of alternatives with an increase in the (maximum) number of iterations. A detailed description of the algorithm for assessing distinctions and corresponding features is described, for example, in [35–37]. The frequency of distinctions depends on the dimension of the MCDA problem (i.e., on the number of criteria and alternatives); if the dimension of the MCDA problems increases, the percentage of differences also increases [35–37]. In the developed module (in the settings), the number of a-cutsNa to analyze the degree of influence of the number of α-cuts on the output results can be specified; in Tables 1–3, Na = 15.
Analysis of distinctions in ranking of alternatives by FTOPSIS models (Tables 1, 2) shows that the influence of the shape of the input FNs used (symmetric/asymmetric TrFNs) is insignificant; the exception is the distinctions between the basic model and the FTRCI model for asymmetric TrFNs (in contrast to the FTRIM model, which differs from the previous one only by the ranking method). According to the estimates, distinctions in ranks of alternatives for FTOPSIS models are significant both for ranking problems (82–90 %) and for the choice problem (57–68 %). With increasing the precision for assessing functions of FNs, from FTTrIM as the least accurate (based on approximate calculations based on propagation of TrFNs through the whole chain of calculations), to FTSIM as more accurate model (with the use of SFA, but not consider the dependence of FNs, in contrast to models with the use of TM: model FTRY and models FTRCI and FTRIM) distinctions are reduced. Distinctions in ranking when comparing the basic model with the "proper" models, FTRCI and FTRIM, can be considered, when using as input symmetric FNs (such FNs, as a rule, are used in applied problems), as small/insignificant (about 3.5 %) for problems of multi-criteria choice and "conditionally acceptable" (9–12 %) for problems of ranking alternatives.
The least of differences in ranks of alternatives for these FTOPSIS models were noted when using linguistic variables (which is very popular in the framework of FMCDA [7, 30]) (Table 3). For models with an approximate approach to the calculating functions of FNs (FTTrIM and FTSIM), we can consider the distinctions for the choice problems as acceptable (5–8.5 %), while for the ranking problems (15–23 %), we can characterize the distinctions as significant. For models with the "proper" calculations, FTRCI and FTRIM, the distinctions in ranks are quite small, both for choice problems (0.4–1.1 %) and for ranking problems (1.8–3.7 %), which in terms of uncertainty/fuzziness is quite an acceptable discrepancy in the framework of decision analysis problems.
Thus, the developed Decerns-FT system makes it possible not only to solve applied multi-criteria problems [17] but also to conduct scientific research within FMCDA [18, 36].
Conclusion
An analysis of existing publications in the field of fuzzy MCDA (FMCDA) shows that all the known papers use approximate methods for estimating functions of fuzzy numbers and, as a rule, one method for ranking fuzzy numbers based on the use of the centroid index (CI).
The paper presents the original Decerns-FT system for solving practical [17] and research [18, 36] problems of multi-criteria decision analysis (MCDA) under conditions of uncertainty/fuzziness. The system implements various methods for evaluating functions of fuzzy arguments and several methods for ranking of fuzzy numbers. The developed Decerns-FT system allowed us to show for the first time [36] that estimates of the ranks of alternatives based on approximate FMCDA models can significantly differ from the corresponding estimates with the use of more accurate models, which implement the transformation method.
The developed library of modules allows using the system for solving a wide range of applied and research problems of FMCDA. The adapted version of the desktop Decerns-FT system is also one of the subsystems of the fuzzy decision support system DecernsFMCDA under creation, which is a further development of the DecernsMCDA system [33] for solving MCDA problems. Algorithms and modules implemented in Decerns-FT are also used in the development of systems (as components of the DecernsFMCDA integrated system), which are fuzzy extensions of such MCDA methods as PROMETHEE, MAVT, FlowSort, and others.
Acknowledgements : This work is supported by the Russian National research project RFBR-19-07-01039.
References
1. Keeney R.L., Raiffa H., Rajala D.W. Decisions with multiple objectives: preferences and value trade-offs. IEEE Transactions on Systems, Man, and Cybernetics, 1979, vol. 9, no. 7, pp. 403. DOI: 10.1109/TSMC.1979.
4310245.
2. Belton V., Stewart T. Multiple Criteria Decision Analysis: An Integrated Approach. Springer US publ., 2002, 372 p. DOI: 10.1007/978-1-4615-1495-4.
3. Greco S., Ehrgott M., Figueira J.R. Multiple Criteria Decision Analysis. State of the Art Surveys. NY, Springer publ., 2016, 1347 p. DOI: 10.1007/978-1-4939-3094-4.
4. Trachtengerz E.A. Computer-Based Decision Support. Moscow, 1998, 376 p. (in Russ.).
5. Larichev O.I. Theory and Methods of Decision-Making. Moscow, 2002, 392 p. (in Russ.).
6. Podinovskij V.V. Ideas and methods for the Importance of Criteria. Moscow, 2019, 103 p. (in Russ.).
7. Kahraman C., Cevik O.S., Oztaysi B. Fuzzy multicriteria decision-making. IJCIS, 2015, vol. 8, no. 4,
pp. 637–666. DOI: 10.1080/18756891.2015.1046325.
8. Mardani A., Jusoh A., Zavadskas E.K. Fuzzy multiple criteria decision-making techniques and applications - Two decades review from 1994 to 2014. Expert Syst. Appl., 2015, vol. 42, no. 8, pp. 4126–4148. DOI: 10.1016/
j.eswa.2015.01.003.
9. Hwang C.-L., Yoon K. Multiple Attribute Decision Making: Methods and Applications. Berlin, Springer-Verlag publ., 1981, 269 p.
10. Chen S.-J., Hwang C.-L. Fuzzy Multiple Attribute Decision Making: Methods and Applications . Berlin, Springer-Verlag publ., 1992, 551 p.
11. Salih M.M., Zaidan B.B., Zaidan A.A., Ahmed M.A. Survey on fuzzy topsis state-of-the-art between 2007–2017. Comput. Oper. Res., 2018, vol. 104, pp. 207–227. DOI: 10.1016/j.cor.2018.12.019.
12. Alcala-Fdez J., Alonso J.M. A survey of fuzzy systems software: Taxonomy, current research trends, and prospects. IEEE Transactions on Fuzzy Systems, 2016, vol. 24, no. 1, pp. 40–56. DOI: 10.1109/TFUZZ.2015.
2426212.
13. Cakir O., Canbolat M.S. A web-based decision support system for multi-criteria inventory classification using fuzzy AHP methodology. Expert Syst. Appl., 2008, vol. 35, no. 3, pp. 1367–1378. DOI: 10.1016/j.eswa.2007.
08.041.
14. Wang X., Kerre E.E. Reasonable properties for the ordering of fuzzy quantities (I). Fuzzy Sets and Systems, 2001, vol. 118, no. 3, pp. 375–385. DOI: 10.1016/S0165-0114(99)00062-7.
15. Hanss M. Applied fuzzy arithmetic: an introduction with engineering applications. Choice Reviews Online, 2005, vol. 43, no. 4, pp. 43–2258. DOI: 10.5860/choice.43-2258.
16. Yatsalo B., Martinez L. Fuzzy rank acceptability analysis: A confidence measure of ranking fuzzy numbers. IEEE Transactions on Fuzzy Systems, 2018, vol. 26, no. 6, pp. 3579–3593. DOI: 10.1109/TFUZZ.2018.2838063.
17. Yatsalo B., Korobov A., Oztaysi B., Kahraman C., Martinez L. A general approach to Fuzzy TOPSIS based on the concept of Fuzzy Multicriteria Acceptability Analysis. Journal of Intelligent and Fuzzy Systems, 2020,
vol. 38, pp. 979–995. DOI: 10.3233/JIFS-179463.
18. Yatsalo B., Korobov A., Martinez L. From MCDA to Fuzzy MCDA: Violation of basic axiom and how to fix it. Neural Comput. and Applic., 2020. Aailable at: https://link.springer.com/article/10.1007%2Fs00521-020-05053-9#citeas (accessed January 16, 2021). DOI: 10.1007/s00521-020-05053-9.
19. Zadeh L. Fuzzy sets. Information and Control, 1965, vol. 8, pp. 338–353.
20. Dubois D., Prade H. Operations on fuzzy numbers. IJSS, 1978, vol. 9, no. 6, pp. 613–626. DOI: 10.1080/
00207727808941724.
21. Lee K.H. First Course on Fuzzy Theory and Applications. In: AINSC, 2005, vol. 27, 345 p. DOI: 10.1007/3-540-32366-x.
22. Pedrycz W., Ekel P., Parreiras R. Fuzzy Multicriteria Decision-Making: Models, Methods and Applications . UK, Chichester, John Wiley & Sons publ., 2010, 338 p. DOI: 10.1002/9780470974032.
23. Klir G.J., Yuan B. Fuzzy Sets and Fuzzy Logic: Theory and Applications. 1995, 574 p.
24. Wang X., Ruan D., Kerre E.E. Mathematics of Fuzziness Basic Issues. Springer-Verlag publ., 2009, 220 p. DOI: 10.1007/978-3-540-78311-4.
25. Nakamura K. Preference relations on a set of fuzzy utilities as a basis for decision making. Fuzzy Sets
and Systems , 1986, vol. 20, no. 2, pp. 147–162. DOI: 10.1016/0165-0114(86)90074-6.
26. Yuan Y. Criteria for evaluating fuzzy ranking methods. Fuzzy Sets and Systems, 1991, vol. 44, no. 2,
pp. 139–157. DOI: 10.1016/0165-0114(91)90073-y.
27. Wang X., Kerre E.E. Reasonable properties for the ordering of fuzzy quantities (II). Fuzzy Sets and Systems, 2001, vol. 118, no. 3, pp. 387–405. DOI: 10.1016/S0165-0114(99)00063-9.
28. Yager R.R. On choosing between fuzzy subsets. Kybernetes, 1980, vol. 9, no. 2, pp.151–154. DOI: 10.1108/
eb005552.
29. Yager R.R. A procedure for ordering fuzzy subsets of the unit interval. Information Sciences, 1981,
vol. 24, no. 2, pp. 143–161. DOI: 10.1016/0020-0255(81)90017-7.
30. Kahraman C., Tolga A.C. An alternative ranking approach and its usage in multi-criteria decision-making. IJCIS, 2009, vol. 2, no. 3, pp. 219–235.
31. Yatsalo B., Korobov A., Martinez L. Fuzzy multi-criteria acceptability analysis: A new approach to multi-criteria decision analysis under fuzzy environment. Expert Sys. Appl., 2017, vol. 84, pp. 262–271. DOI: 10.1016/
j.eswa.2017.05.005.
32 Zadeh L. The concept of a linguistic variable and its applications to approximate reasoning. Information Sciences, pt. 1. DOI: 10.1016/0020-0255(75)90036-5; pt. 2. DOI: 10.1016/0020-0255(75)90046-8; pt. 3. DOI: 10.
1016/0020-0255(75)90017-1.
33. Yatsalo B.I., Gritsyuk S.V., Didenko V.I., Mirseabasov O.A. The system for multi-criteria decision analysis DecernsMCDA and its practical application. Software and Systems, 2014, no. 2, pp. 73–84 (in Russ.).
34. Yatsalo B., Didenko V., Gritsyuk S., Sullivan T. Decerns: A framework for multi-criteria decision analysis. IJCIS, 2015, vol. 8, no. 3, pp. 467–489. DOI: 10.1080/18756891.2015.1023586.
35. Yatsalo B., Korobov A., Oztaysi B., Kahraman C., Martinez L. Fuzzy extensions of PROMETHEE: Models of different complexity with different ranking methods and their comparison. Fuzzy Sets and Systems, 2020. Available at: https://www.sciencedirect.com/science/article/abs/pii/S0165011420303213?via%3Dihub (accessed January 16, 2021). DOI: 10.1016/j.fss.2020.08.015.
36. Yatsalo B., Korobov A. Different approaches to fuzzy extension of an MCDA method and their comparison. In: Advances in Intelligent Systems and Computing Series, 2021, pp.709–717. DOI: 10.1007/978-3-030-51156-2_82.
37. Yatsalo B., Korobov A., Martinez L. Presumption of model adequacy in fuzzy multi-criteria decision analysis. Developments of Artificial Intelligence Technologies in Computation and Robotics. Proc. FLINS , 2020,
pp. 759–766.
УДК 004.89
DOI: 10.15827/2311-6749.21.1.1
Система поддержки принятия решений Decerns-FT для анализа многокритериальных задач
в условиях нечеткости
А.В. Коробов 1 , аспирант, alexander.korobov.1993@gmail.com
Б.И. Яцало 1 , д.т.н., профессор, yatsalo@gmail.com
1 Национальный исследовательский ядерный университет МИФИ (ИАТЭ НИЯУ МИФИ), отделение интеллектуальных кибернетических систем, Обнинск, 249040, Россия
В основе нечеткого многокритериального анализа решений (НМКАР) лежат операции оценки функций от нечетких аргументов и ранжирования нечетких чисел. В общем случае реализация каждой из указанных операций требует использования соответствующих компьютерных модулей. Все известные на настоящее время системы НМКАР базируются на приближенных оценках функций от нечетких аргументов. Целью представленной работы является создание и научно-практическое применение системы НМКАР, реализующей все основные подходы к оценке функций от нечетких чисел, а также различные методы ранжирования нечетких чисел на примере нечеткого расширения классического метода многокритериального анализа решения TOPSIS.
В работе представлены функциональные возможности разработанной компьютерной системы Decerns-FT и ее особенности, включающие возможность использования нечетких моделей FTOPSIS различного уровня сложности в зависимости от выбранного метода оценки функций от нечетких аргументов и метода ранжирования нечетких чисел. Описана общая структура системы и ее основные блоки. Приведен пример использования Decerns-FT для анализа различий в ранжировании альтернатив многокритериальных задач разработанными моделями FTOPSIS с применением приближенных методов оценки функций от нечетких чисел, методов стандартной нечеткой арифметики, а также редуцированного и общего метода трансформации. В рамках решения данной задачи используется модуль Монте-Карло для генерации большого числа сценариев многокритериальных задач. С использованием системы Decerns-FT впервые показано, что различия в ранжировании альтернатив многокритериальных задач моделями FTOPSIS, отличающимися подходами к оценке функций от нечетких чисел и методами ранжирования, являются значимыми.
Разработанная компьютерная система Decerns-FT не имеет аналогов в классе систем, реализующих модели НМКАР. Модули системы Decerns-FT формируют основу для создания других систем НМКАР, являющихся компонентами системы поддержки принятия решений DecernsFMCDA, предназначенной для решения широкого круга научно-прикладных задач многокритериального анализа решений в условиях неопределенности/нечеткости, а также для использования в рамках соответствующих университетских курсов и для тренинга специалистов.
Ключевые слова: нечеткие числа, ранжирование нечетких чисел, нечеткий многокритериальный анализ решений, Fuzzy TOPSIS, нечеткая система, Decerns.
Благодарности. Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта
№ 19-07-01039.
Литература
1. Keeney R.L., Raiffa H., Rajala D.W. Decisions with multiple objectives: preferences and value trade-offs. IEEE Transactions on Systems, Man, and Cybernetics, 1979, vol. 9, no. 7, pp. 403. DOI: 10.1109/TSMC.1979.
4310245.
2. Belton V., Stewart T. Multiple Criteria Decision Analysis: An Integrated Approach. Springer US publ., 2002, 372 p. DOI: 10.1007/978-1-4615-1495-4.
3. Greco S., Ehrgott M., Figueira J.R. Multiple Criteria Decision Analysis. State of the Art Surveys. NY, Springer publ., 2016, 1347 p. DOI: 10.1007/978-1-4939-3094-4.
4. Трахтенгерц Э.А. Компьютерная поддержка принятия решений. M.: Синтег, 1998. 376 с.
5. Ларичев О.И. Теория и методы принятия решений. M.: Физматкнига, 2002. 392 с.
6. Подиновский В.В. Идеи и методы важности критериев. M.: Наука, 2019. 103 с.
7. Kahraman C., Cevik O.S., Oztaysi B. Fuzzy multicriteria decision-making. IJCIS, 2015, vol. 8, no. 4,
pp. 637–666. DOI: 10.1080/18756891.2015.1046325.
8. Mardani A., Jusoh A., Zavadskas E.K. Fuzzy multiple criteria decision-making techniques and applications -
Two decades review from 1994 to 2014. Expert Syst. Appl., 2015, vol. 42, no. 8, pp. 4126–4148. DOI: 10.1016/
j.eswa.2015.01.003.
9. Hwang C.-L., Yoon K. Multiple Attribute Decision Making: Methods and Applications. Berlin, Springer-Verlag publ., 1981, 269 p.
10. Chen S.-J., Hwang C.-L. Fuzzy Multiple Attribute Decision Making: Methods and Applications. Berlin, Springer-Verlag publ., 1992, 551 p.
11. Salih M.M., Zaidan B.B., Zaidan A.A., Ahmed M.A. Survey on fuzzy topsis state-of-the-art between 2007–2017. Comput. Oper. Res., 2018, vol. 104, pp. 207–227. DOI: 10.1016/j.cor.2018.12.019.
12. Alcala-Fdez J., Alonso J.M. A survey of fuzzy systems software: Taxonomy, current research trends, and prospects. IEEE Transactions on Fuzzy Systems, 2016, vol. 24, no. 1, pp. 40–56. DOI: 10.1109/TFUZZ.2015.
2426212.
13. Cakir O., Canbolat M.S. A web-based decision support system for multi-criteria inventory classification using fuzzy AHP methodology. Expert Syst. Appl., 2008, vol. 35, no. 3, pp. 1367–1378. DOI: 10.1016/j.eswa.
2007.08.041.
14. Wang X., Kerre E.E. Reasonable properties for the ordering of fuzzy quantities (I). Fuzzy Sets and Systems, 2001, vol. 118, no. 3, pp. 375–385. DOI: 10.1016/S0165-0114(99)00062-7.
15. Hanss M. Applied fuzzy arithmetic: an introduction with engineering applications. Choice Reviews Online, 2005, vol. 43, no. 4, pp. 43–2258. DOI: 10.5860/choice.43-2258.
16. Yatsalo B., Martinez L. Fuzzy rank acceptability analysis: A confidence measure of ranking fuzzy numbers. IEEE Transactions on Fuzzy Systems, 2018, vol. 26, no. 6, pp. 3579–3593. DOI: 10.1109/TFUZZ.2018.2838063.
17. Yatsalo B., Korobov A., Oztaysi B., Kahraman C., Martinez L. A general approach to Fuzzy TOPSIS based on the concept of Fuzzy multicriteria acceptability analysis. Journal of Intelligent and Fuzzy Systems, 2020,
vol. 38, pp. 979–995. DOI: 10.3233/JIFS-179463.
18. Yatsalo B., Korobov A., Martinez L. From MCDA to Fuzzy MCDA: Violation of basic axiom and how to fix it. Neural Comput. and Applic., 2020. URL: https://link.springer.com/article/10.1007%2Fs00521-020-05053-
9#citeas (дата обращения: 16.01.2021). DOI: 10.1007/s00521-020-05053-9.
19. Zadeh L. Fuzzy sets. Information and Control, 1965, vol. 8, pp. 338–353.
20. Dubois D., Prade H. Operations on fuzzy numbers. IJSS, 1978, vol. 9, no. 6, pp. 613–626. DOI: 10.1080/
00207727808941724.
21. Lee K.H. First Course on Fuzzy Theory and Applications. In: AINSC, 2005, vol. 27, 345 p. DOI: 10.1007/
3-540-32366-x.
22. Pedrycz W., Ekel P., Parreiras R. Fuzzy Multicriteria Decision-Making: Models, Methods and Applications. UK, Chichester, John Wiley & Sons publ., 2010, 338 p. DOI: 10.1002/9780470974032.
23. Klir G.J., Yuan B. Fuzzy sets and fuzzy logic: theory and applications. 1995, 574 p.
24. Wang X., Ruan D., Kerre E.E. Mathematics of Fuzziness Basic Issues. Springer-Verlag publ., 2009, 220 p. DOI: 10.1007/978-3-540-78311-4.
25. Nakamura K. Preference relations on a set of fuzzy utilities as a basis for decision making. Fuzzy Sets and Systems, 1986, vol. 20, no. 2, pp. 147–162. DOI: 10.1016/0165-0114(86)90074-6.
26. Yuan Y. Criteria for evaluating fuzzy ranking methods. Fuzzy Sets and Systems, 1991, vol. 44, no. 2,
pp. 139–157. DOI: 10.1016/0165-0114(91)90073-y.
27. Wang X., Kerre E.E. Reasonable properties for the ordering of fuzzy quantities (II). Fuzzy Sets and Systems, 2001, vol. 118, no. 3, pp. 387–405. DOI: 10.1016/S0165-0114(99)00063-9.
28. Yager R.R. On choosing between fuzzy subsets. Kybernetes, 1980, vol. 9, no. 2, pp.151–154. DOI: 10.
1108/eb005552.
29. Yager R.R. A procedure for ordering fuzzy subsets of the unit interval. Information Sciences, 1981,
vol. 24, no. 2, pp. 143–161. DOI: 10.1016/0020-0255(81)90017-7.
30. Kahraman C., Tolga A.C. An alternative ranking approach and its usage in multi-criteria decision-making. IJCIS, 2009, vol. 2, no. 3, pp. 219–235.
31. Yatsalo B., Korobov A., Martinez L. Fuzzy multi-criteria acceptability analysis: A new approach to multi-criteria decision analysis under fuzzy environment. Expert Sys. Appl., 2017, vol. 84, pp. 262–271. DOI: 10.1016/
j.eswa.2017.05.005.
32. Zadeh L. The concept of a linguistic variable and its applications to approximate reasoning. Information Sciences, pt. 1. DOI: 10.1016/0020-0255(75)90036-5; pt. 2. DOI: 10.1016/0020-0255(75)90046-8; pt. 3. DOI: 10.
1016/0020-0255(75)90017-1.
33. Яцало Б.И., Грицюк С.В., Диденко В.И., Мирзеабасов О.А. Система многокритериального анализа решений DecernsMCDA и ее практическое применение // Программные Продукты и Системы. 2014.№ 2. С. 73–84.
34. Yatsalo B., Didenko V., Gritsyuk S., Sullivan T. Decerns: A framework for multi-criteria decision analysis. IJCIS, 2015, vol. 8, no. 3, pp. 467–489. DOI: 10.1080/18756891.2015.1023586.
35. Yatsalo B., Korobov A., Oztaysi B., Kahraman C., Martinez L. Fuzzy extensions of PROMETHEE: Models of different complexity with different ranking methods and their comparison. Fuzzy Sets and Systems, 2020.
URL: https://www.sciencedirect.com/science/article/abs/pii/S0165011420303213?via%3Dihub (дата обращения: 16.01.2021). DOI: 10.1016/j.fss.2020.08.015.
36. Yatsalo B., Korobov A. Different approaches to fuzzy extension of an MCDA method and their comparison. In: Advances in Intelligent Systems and Computing Series, 2021, pp.709–717. DOI: 10.1007/978-3-030-51156-2_82.
37. Yatsalo B., Korobov A., Martinez L. Presumption of model adequacy in fuzzy multi-criteria decision analysis. Developments of Artificial Intelligence Technologies in Computation and Robotics. Proc. FLINS, 2020,
pp. 759–766.





Comments