При решении практических оптимизационных задач часто приходится иметь дело с многомерными овражными и многоэкстремальными целевыми функциями. Несмотря на большое количество методов многомерной минимизации [1], вопрос о выборе эффективного алгоритма глобальной минимизации функций большой размерности все еще представляется актуальным. Для глобальной минимизации таких функций используются специальные алгоритмы и пакеты прикладных программ, такие как MATLAB, LINGO, MINITAB, GAMS [2]. Так, в пакете MATLAB существует объект GlobalSearch, который позволяет вести поиск глобального минимума с автоматической генерацией множества пробных точек.

Так как точность и время решения таких задач зависят от удачного выбора начального приближения, наряду с детерминированными методами большое распространение получили и вероятностные подходы, основанные на имитации различных процессов и явлений: отжиг, рой пчел, поведение муравьев, генетический процесс и т.д. Развиваются алгоритмы с метаэвристическими [3], гибридными и метаоптимизационными концепциями [4].

Поиск глобального минимума непрерывно дифференцируемых функций предпочтительнее проводить с помощью производных. В данной статье приводится алгоритм, основанный на имитации конвективно-диффузионного процесса, описываемого системой дифференциальных уравнений. В методе используются концепции диффузионного сглаживания поверхности целевой функции [5] и сведение многомерной минимизации к одномерной [6]. Для оценки эффективности предлагаемого подхода в среде MATLAB разработаны специальная функция и алгоритм глобальной минимизации.

Конвективно-диффузионный метод минимизации

В предлагаемом методе многомерной минимизации имитируется процесс конвективно-диффузионного перемещения частиц многокомпонентного потока в многомерном пространстве. Искомые переменные одновременно являются концентрациями многокомпонентного потока и координатами многомерного пространства, а процесс минимизации описывается системой одномерных дифференциальных уравнений [7]:

                                         (1)

где c_i – искомые переменные; D – настраиваемый диффузионный параметр оптимизации, имеющий малые значения (D = 0.01÷0.1); v_i(c) – скорости движения, равные нормированным частным производным целевой функции f( c) с противоположным знаком:

Здесь c = (c₁, c₂, …, c_n) – вектор искомых переменных; τ – время; l – координата на единичном отрезке.

Уравнения (1) интегрируются до наступления стационарного состояния с начальными и граничными условиями:

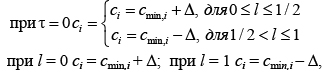                     (2)

где c_min,i и ∆ – величины для определения области поиска минимума (∆ > 0).

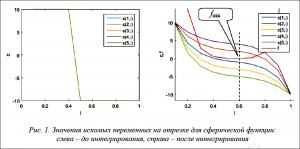
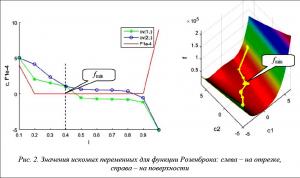
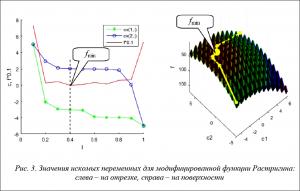
В результате решения данной краевой задачи получается установившееся распределение значений искомых переменных и функции на отрезке, а многомерная минимизация сводится к минимизации одномерной функции f(l), как показано на рисунках 1–3 при минимизации функций:

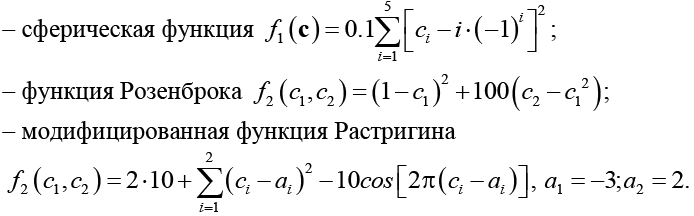
Влияние диффузионного параметра

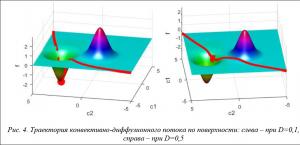
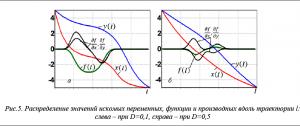
Дифференциальные уравнения (1) необходимо интегрировать по возможности с малыми значениями коэффициентов диффузии D. Влияние данного параметра продемонстрировано на рисунках 4 и 5 при минимизации функции

с разными коэффициентами D.

Метод интегрирования уравнений конвективной диффузии

Интегрирование уравнений (1) выполняется по неявной разностной схеме:

          (3)

с граничными и начальными условиями

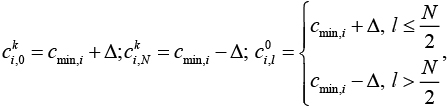                                                      (4)

где N – количество точек; τ – шаг интегрирования по времени.

Алгебраические уравнения (3) можно переписать в виде системы, которая решается методом прогонки:

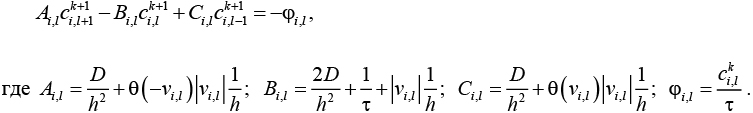
На каждой итерации вычисляется максимальная разность

Если e_k > e_{k -1}, то шаг интегрирования τ уменьшается в два раза. Критерием завершения расчетов является e_k < ε, где ε – малое положительное число. Искомыми решениями c_i,min являются значения переменных в точке с минимальным значением целевой функции f( l) на отрезке.

Ниже приведен текст разработанной функции cdmin.m в среде MATLAB для многомерной минимизации конвективно-диффузионным методом.

Функция в MATLAB для минимизации конвективно-диффузионным методом

[cv, lmin, fmin, it] = cdmin(funm, cv, d0, tau, eps, nitmax)

Входные параметры :

funm – адрес m-функции вида [fi, dfi] = func(x) для вычисления значений целевой функции и ее частных производных;

cv [nv, nl] – начальные значения искомых переменных в точках отрезка;

nv – количество переменных;

nl – количество точек на отрезке;

d0 – коэффициент диффузии;

tau – начальный шаг интегрирования;

eps – заданная точность;

nitmax – максимально допустимое количество итераций.

Выходные параметры :

cv [nv, nl] – полученные значения искомых переменных в точках отрезка;

lmin – точка с минимальным значением целевой функции;

fmin – найденное минимальное значение целевой функции;

it – количество выполненных итераций.

Текст функции cdmin.m

function [cv, lmin, fmin, it] = cdmin(funm,  cv, d0, tau, eps, nitmax)

% CDMIN – конвективно-диффзионный метод минимизации, автор – Федоров В.В.

nv=length(cv(:,1)); nl=length(cv(1,:)); h=1./(nl-1);

global fl dfl;

fl=zeros(nl,1); dfl=zeros(nv,nl);

calcdlen(cv, funm);

it=0; e=1e50;

while (it<nitmax)&&(e>eps)

    cv0=cv; eps0=e;

    cv=calcm(cv0, d0,tau,h);

    e=max(max(abs(cv-cv0)));

    if e>eps0

        tau=tau*0.5; cv=cv0;

    else

        calcdlen(cv, funm);

    end;

    it=it+1;

end;

% точка минимума

fl(1)=funm(cv(:,1)); fl(nl)=funm(cv(:,nl));

[fmin, lmin]=min(fl(:));

end

%--метод прогонки -------------------------------

function cv = calcm(cv, d0,tau,h)

global dfl;

nv=length(cv(:,1)); nl=length(cv(1,:));

p=zeros(1,nl); r=zeros(1,nl); p(2)=0;

for k=1:nv

    r(2)=cv(k,1);

    for l=2:nl-1

        [ a, b, c ] = abc(dfl(k,l), d0,tau,h);

        av=b-c*p(l); p(l+1)=a/av; fi=cv(k,l)+c*r(l); r(l+1)=fi/av;

    end;

    for l=nl-1:-1:2

        cv(k,l)=r(l+1)+p(l+1)*cv(k,l+1);

    end;

end;

end

%---производные в точках отрезка------------------

function id = calcdlen(cv, funm)

global fl dfl;

nl=length(cv(1,:));

for l=2:nl-1

    [fl(l), dfl(:,l)]=funm(cv(:,l));

    s=norm(dfl(:,l));

    if s>0

        dfl(:,l)=dfl(:,l)/s;

    end;

end;

id=0;

end

%--коэффициенты метода прогонки----------------------------

function [ aa, bb, cc ] = abc(df,d0,tau,h )

d = d0/h*tau; vel = -df*tau/h; aa = d/h; cc = d/h; bb = 2.*d/h +1;

if vel>0

    bb = bb + vel; cc = cc +vel;

else

    bb = bb - vel; aa = aa - vel;

end;

end

 

В качестве примера приведен скрипт для минимизации функции Розенброка размерности nv=100 с помощью cdmin.

Пример минимизации функции Розенброка

Файл froz.m для вычисления значений целевой функции и частных производных:

function [fi,dfi] = froz(x)

%функция Розенброка

nv=length(x);

fi=0;

for i=1:nv-1

    fi=fi+100*(x(i+1)-x(i)^2)^2+(1-x(i))^2;

end;

if nargout > 1

    dfi=zeros(nv,1);

    for i=2:nv-1

        dfi(i)=-200*x(i-1)^2+400*x(i)^3+2*x(i)*(101-200*x(i+1))-2;

    end;

    dfi(1)=400*x(1)^3+2*x(1)*(1-200*x(2))-2;

    dfi(nv)=200*x(nv)-200*x(nv-1)^2;

end;

end

Скрипт для минимизации функции Розенброка с помощью cdmin.m:

d0=0.01; tau=1.0; eps=1.e-6; nitmax=10000; % параметры оптимизации

a=-5; b=5; % границы

nl=10; nv=100; % количество точек и переменных

clearvars cv;

cv=zeros(nv,nl);

% начальные и граничные условия

lm=round(0.5*nl);

for l=1:lm-1

    cv(:,l)=b;

end;

for l=lm:nl

    cv(:,l)=a;

end;

[cv, lmin, fmin, it] = cdmin(@froz, cv, d0,  tau, eps, nitmax);

it

[max(cv(:,lmin)), min(cv(:,lmin))]

fmin

it =

        1021

ans =

    1.0000    0.9806

fmin =

   1.6141e-04

Максимальное и минимальное значения искомых переменных равны 1.0000 и 0.9806 соответственно.

Для сравнения далее приведены результаты, полученные квазиньютоновским методом с помощью встроенной функции fminunc:

с произвольным начальным приближением x0 в интервале (-1, 2):

options = optimoptions(@fminunc,'Algorithm','quasi-newton','TolX',eps);

a = -1; b = 2;

x0 = (b-a).*rand(nv,1) + a;

[x,fmin2] = fminunc(@froz,x0,options);

[max(x), min(x)]

fmin2

ans =

    0.9963    0.0005

fmin2 =

88.6344

с начальным приближением cv(:, lmin)), полученным с помощью cdmin:

[x,fmin2] = fminunc(@froz,cv(:,lmin));

[max(x), min(x)]

fmin2

ans =

    1.0000    1.0000

fmin2 =

   8.7827e-11

Из примера видно, что точка, найденная конвективно-диффузионным методом, находится близко к точке глобального минимума, а полученные значения переменных легко уточняются в окрестности этой точки. Тем не менее, для глобальной минимизации многоэкстремальных функций конвективно-диффузионным методом предлагается алгоритм дополнительного поиска в разных областях.

Алгоритм глобальной минимизации

Предлагаемый алгоритм аналогичен алгоритму поиска локального минимума с помощью градиентов с той лишь разницей, что в роли шага здесь выступает ширина области, а положение точки минимума уточняется решением нестационарной краевой задачи с уравнениями конвективной диффузии.

Алгоритм

1. Выбираются начальное приближение c_{min, i} и параметр ширины области ∆.

2. Задается распределение значений переменных c⁰ _i,l на отрезке согласно начальным и граничным условиям 4.

3. Вычисляются координаты c’_{min, i} точки минимума с помощью функции cdmin.

4. Если в данной точке получено меньшее значение целевой функции, то вычисляется отклонение новых значений c’_min,i от предыдущих c_min,i; принимаются новые значения: c_min,i = c’ _min,i, в противном случае параметр ∆ уменьшается в два раза.

5. Если рассчитанное отклонение меньше допустимой величины или количество итераций превышает допустимое число, то поиск заканчивается, в противном случае поиск продолжается с пункта 2.

Для реализации данного алгоритма составлен скрипт, приведенный далее. В качестве примера взята функция Экли с произвольными координатами a _i точки минимума:

                        (5)

где

Частные производные функции:

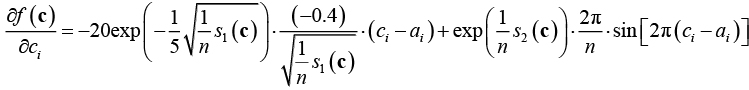
Файл fackley.m для вычисления значений целевой функции и частных производных:

function [fi,dfi] = fackley(x)

%функция Экли

global ai;

nv=length(x);

s1=sum((x(:)-ai(:)).^2);

s2=sum( cos( 2*pi*(x(:)-ai(:)) ) );

v1=-20*exp(-0.2*(s1/nv)^0.5);

v2=-exp(s2/nv);

fi=v1+v2 +exp(1)+20;

if nargout > 1

    dfi=zeros(nv,1);

    a1=-0.4*v1/(s1/nv)^0.5;

    a2=-v2/nv*2*pi;

    dfi(:)=a1*(x(:)-ai(:))+a2*sin(2*pi*(x(:)-ai(:)));

end;

end

Скрипт для поиска глобального минимума с помощью m-функции cdmin

d0=0.1; tau=1.0; eps=1.e-4; %параметры оптимизации

nitmax=1000;nitmax2=100;%допустимые количества итераций

delta0=10.0; %параметр ширины области

func=@fackley; %адрес функции

clearvars cv cmin ai;

nv=10; nl=10; %количество переменных и точек на отрезке

v1=zeros(nv,1); v2=zeros(nv,1); cv=zeros(nv,nl);

global ai;

ai=(2*delta0).*rand(nv,1)-delta0;%генерация координат точки минимума

cmin=zeros(nv,1); %начальное приближение

 

%--------- алгоритм поиска глобального минимума с cdmin--------------

delta=delta0;

f1=1e50; dc=1e50; nit=0; lm=round(0.5*nl);

while (nit<nitmax2)&&(dc>eps)

    for l=1:lm-1

        cv(:,l)=cmin(:)+delta;

    end;

    for l=lm:nl

        cv(:,l)=cmin(:)-delta;

    end;

    [cv, lmin, fmin, it] = cdmin(func, cv, d0,  tau, eps, nitmax );

    if (fmin<f1)||(nit==0)

        dc=norm(cmin(:)-cv(:,lmin));%отклонение значений переменных

        cmin(:)=cv(:,lmin);

        f1=fmin;

    else

        delta=0.5*delta;

    end;

    nit=nit+1;

end;

%--------вывод результатов-----------------------------------------

nit, f1, cmin', ai'

 

nit =

    28

f1 =

   8.1581e-05

ans =

    7.9179   -8.0182   -9.1167    1.1459    5.4499   -3.7612   -6.4203   -3.2209   -5.7971    0.2031

ans =

    7.9178   -8.0182   -9.1167    1.1459    5.4499   -3.7612   -6.4204   -3.2209   -5.7971    0.2031

Получаемые значения переменных хорошо совпадают со значениями координат точки минимума.

Иллюстрация алгоритма

Для графического представления процесса глобальной минимизации с приведенным алгоритмом взята двумерная функция Экли с точкой минимума (0, 0), находящейся за пределами принятой начальной области поиска (5 ≤ c₁ ≤15; 2 ≤ c₂ ≤ 12):

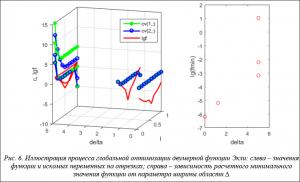
На рисунке 6 в левой части изображены результаты решения задачи (1) с разными граничными условиями в соответствии с алгоритмом, в правой – найденные минимальные значения целевой функции в данных областях.

Как видно на рисунке 7, несмотря на то, что поиск минимума начался в области, не содержащей точку глобального минимума, уточнение граничных условий по приведенному алгоритму позволило перейти к необходимой области и найти в ней глобальный минимум.

Эффективность алгоритма глобальной минимизации

Оценка сложности метода минимизации

Так как алгоритм основан на многократном решении краевой задачи 1, его эффективность прежде всего зависит от сложности численного интегрирования системы дифференциальных уравнений до наступления стационарного состояния. Временную сложность можно определить по формуле

t (n) = I(n)·φ(n) · n· τ,                           (6)

где I(n) – количество необходимых итераций; φ(n) – сложность вычисления производной целевой функции; n – размерность минимизации; τ – время одной итерации для одного уравнения конвективной диффузии.

При I = const и φ = const зависимость сложности от размерности (временная сложность) должна быть прямо пропорциональна n:

t (n) = O(n),                                            (7)

что, собственно, и подтверждается результатами численных экспериментов, приведенных в [7].

Данное свойство является основным достоинством конвективно-диффузионного метода минимизации. Тем не менее, для оценки эффективности разработанного алгоритма требуется его сравнение с другими алгоритмами.

Численные эксперименты для сравнительной оценки алгоритма

Эксперименты проводились с овражной функцией Розенброка

и многоэкстремальными функциями Растригина и Экли со случайными координатами глобального минимума:

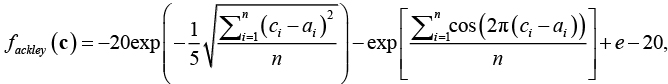
где -10 ≤ a_i ≤ 10.

Поиск глобального минимума тестовых функций осуществлялся в среде MATLAB по разработанному алгоритму с помощью уравнений конвективной диффузии и для сравнения методами глобального и прямого поиска – GlobalSearch и fminsearch. Эффективность алгоритма оценивалась по двум критериям: время поиска и найденное минимальное значение целевой функции.

Как известно, алгоритмы нулевого порядка обычно используются для сложных функций, вычисление производных которых не представляется возможным или требует больших временных затрат. Поэтому при сравнении с методом прямого поиска в предлагаемом алгоритме производные вычислялись так, как для сложной функции с помощью конечных разностей:

где δ – малое число, принятое равным 1·10^-3.

Скрипт для проведения численных экспериментов:

nitmax=1000; nitmax2=100; %допустимые количества итераций

delta0=10.0;

 

func=@froz;

fname='Функция Розенброка';

 

% func=@fras;

% fname='Функция Растригина';

 

% func=@fackley;

% fname='Функция Экли';

 

clc;

hc1=figure;

hc2=figure;

 

for nv=10:10:100

    clearvars cv cmin v1 v2 ai x0 xb xe;

   

    xb=zeros(nv,1);

    xe=zeros(nv,1);

    delta=delta0;

   

    %---генерация случайных координат для функций Растригина и Экли

    global ai;

    ai = 2*delta0.*rand(nv,1) - delta0;

    %--------------------------------------------------------------

   

    cmin=zeros(nv,1);

    cv=zeros(nv,nl);

   

    tb=cputime;

    f1=1e50; dc=1e50; nit=0;

    lm=round(0.5*nl);

    while (nit<nitmax2)&&(dc>eps)

        for l=1:lm-1

            cv(:,l)=cmin(:)+delta;

        end;

        for l=lm:nl

            cv(:,l)=cmin(:)-delta;

        end;

        [cv, lmin, fmin, it] = cdmin(func, cv, d0,  tau, eps, nitmax );

        if (fmin<f1)||(nit==0)

            dc=norm(cmin(:)-cv(:,lmin));

            cmin(:)=cv(:,lmin);

            f1=fmin;

        else

            delta=0.5*delta;

        end;

        nit=nit+1;

    end;

    [cmin,fcdmin] = gradf(func,cmin,eps*1.e-3); %уточнение градиентным методом

    te=cputime;

    tcdmin = (te-tb)*1000;

   

    x0=zeros(nv,1);

   

    %----- для сравнения с методом глобального поиска GlobalSearch

    xb(:)=-delta0; xe(:)=delta0;

    tb=cputime;

    opts = optimset('Algorithm','interior-point','GradObj','on','tolX',eps);

    problem = createOptimProblem('fmincon','objective',func, 'x0', x0,'lb',xb,'ub',xe, 'options', opts);

    gs = GlobalSearch;

    [x2,f2] = run(gs,problem);

    te=cputime;

    t2 = (te-tb)*1000;

   

    %----- для сравнения с методом прямого поиска fminsearch

    %         options=optimset('tolX',eps,'MaxFunEvals',10000000,'MaxIter',10000000);

    %         tb=cputime;

    %         [x3, f2]=fminsearch(func, x0, options);

    %         te=cputime;

    %         t2 = (te-tb)*1000;

    %-----

 

    %----- вывод результатов в графическом виде

    figure(hc1);

    ms=8;

    stem(nv,tcdmin,'r','filled','Marker','o','MarkerSize',ms);

    hold on;

    stem(nv,t2,'b','filled','Marker','*','MarkerSize',ms*1.5);

    hold on;

    figure(hc2);

    stem(nv,fcdmin,'r','filled','Marker','o','MarkerSize',ms);

    hold on;

    stem(nv,f2,'b','filled','Marker','*','MarkerSize',ms*1.5);

    hold on;

    nv

end;

 

%----- параметры фигур

figure(hc1);

xlabel('n');

ylabel('t, мс');

legend('tcdmin','t2');

title(fname);

figure(hc2);

xlabel('n');

ylabel('f');

legend('fcdmin','f2');

title(fname);

fpos1 = [100 100 400 200];

hc1.Position = fpos1;

fpos2 = [500 100 400 200];

hc2.Position = fpos2;

 

В данном скрипте предусмотрено уточнение координат полученной точки градиентным методом, скрипт которого приведен ниже:

 

function [ c, f ] = gradf(funm, c0, eps)

nv=length(c0);

c=zeros(nv,1);

al=1; e=1;

[f0,dfi]=funm(c0);

while (e>eps)

    s=norm(dfi);

    if s>0

        dfi=dfi/s;

    end;

    c(:)=c0(:)-dfi(:)*al;

    [f,dfi]=funm(c);

    if f>f0

        al=al*0.5; c=c0;

    else

        e=norm(c-c0);

        f0=f; c0=c;

    end;

end;

end

Результаты численных экспериментов

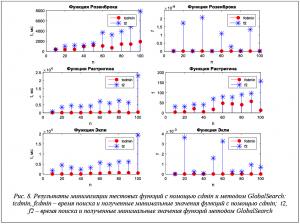
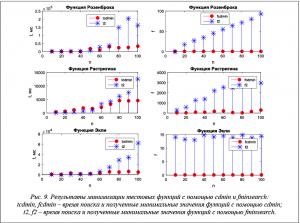
Результаты численных экспериментов для сравнительной оценки разработанного алгоритма с методами глобального и прямого поиска (GlobalSearch и fminsearch) приведены, соответственно, на рисунках 8 и 9.

Во всех случаях при минимизации конвективно-диффузионным методом были получены меньшие значения тестовых функций.

Из рисунка 8 видно, что, благодаря свойству (7), затраченное время поиска с помощью cdmin значительно ниже времени поиска методом GlobalSearch.

Для сравнения с методом прямого поиска fminsearch в разработанном алгоритме с cdmin частные производные вычислялись как для сложной функции с помощью конечных разностей. Тем не менее, как показано на рисунке 9, затраченное время поиска с помощью cdmin в данном случае также ниже для функций большой размерности.

Результаты численных экспериментов свидетельствуют о том, что разработанный алгоритм глобальной минимизации с помощью уравнений конвективной диффузии является более эффективным для дифференцируемых многоэкстремальных функций большой размерности.

Выводы

Результаты проведенных численных экспериментов в среде MATLAB подтверждают применимость разработанного алгоритма для глобальной минимизации непрерывно-дифференцируемых многоэкстремальных целевых функций большой размерности. Предлагаемый подход минимизации с помощью уравнений конвективной диффузии может также стать основой для разработки алгоритма многомерной минимизации с ограничениями.

Литература

1. Захарова Е.М., Минашина И.К. Обзор методов многомерной оптимизации // Информационные процессы. 2014. Т. 14. № 3. С. 256–274.

2. Suman Dutta. Optimization in Chemical Engineering. s.l. Cambridge Univ. Press, 2015. DOI: 10.1017/CBO9781316134504.

3. Du K.-L., Swamy M.N.s. Search and Optimization by Metaheuristics. 2016, 437 р. DOI: 10.1007/978-3-319-41192-7.

4. Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой. М.: Изд-во МГТУ им. Н.Э. Баумана, 2017. С. 448.

5. Piela L., Kostrowicki J., and Scheraga H.A.. The multiple-minima problem in the conformational analysis of molecules. Deformation of the potential energy hypersurface by the diffusion equation method. J. of Physical Chemistry. 1989, no. 93, pp. 3339–3346.

6. Snyman A.J. A new and dynamic method for unconstrained optimization. Applied Mathematical Modelling, 1982, vol. 6, pp. 449–462.

7. Федоров В.В. Новый конвективно-диффузионный метод глобальной минимизации для решения обратных задач химической кинетики // Наука и образование. 2013. № 4. DOI: 10.7463/0413.0569246.