В химической технологии существуют процессы, математическое описание которых построено на основе обыкновенных дифференциальных уравнений модели идеального смешения, и объекты, математическое описание которых построено на основе дифференциальных уравнений в частных производных. Все остальные классы моделей типовых процессов химической технологии: диффузионные, ячеечные и комбинированные модели – являются производными от этих двух классов.
Перечислим основные математические свойства вышеназванных классов моделей технологических операторов в форме основных формулировок теорем, взятых из теории дифференциальных уравнений, например [1–4], которые в данной работе характеризуют требования, предъявляемые к математическим моделям химико-технологических процессов (ХТП), и выступают в качестве накладываемых на них ограничений.
Модели идеального смешения
Теорема 1. Существование и единственность решений [1].
Пусть задана система нормальных уравнений:
d(xi)/dt = fi (t, x1, ..., xn). (1)
Правые части уравнений fi (t, x1, ..., xn), где i=1, ..., n, определены в некотором параллелепипеде D:
|t-t0|<a, |xi-xi(0)|<b, где i=1, ..., n, (2)
с центром в некоторой начальной точке (t(0), x1(0), ..., xn(0)) и удовлетворяют в нем двум условиям:
fi непрерывны и, следовательно, ограничены:
|fi(t, x1, ..., xn)|£M, где i=1, ..., n; (3)
fi удовлетворяют условиям Липшица относительно переменных x1, ..., xn:
S|fi(t, x1(1), ..., xn(1))-fi(t, x1(2), ..., xn(2))|£LS|xi(1)-xi(2)|, (4)
где i=1, ..., n; L – постоянное положительное число, а (t, x1(1), ..., xn(1)) и (t,x1(2), ..., xn(2)) – любые точки из R, при этом система имеет единственное решение:
x1=x1(t), x2=x2(t), ..., xn=xn(t), (5)
удовлетворяющее начальным условиям
x1=x1(0), x2=x2(0), ..., xn=xn(0) при t=t(0), (6)
определенное (и непрерывно дифференцируемое) в интервале
|x-x0|£h, (7)
где h=min (a, b/M). (8)
Это решение не выходит из параллелепипеда D при |t-t0|<h, то есть
|xi(t)-xi(0)|<b (i=1, 2, ..., n) при |t-t0|<h. (9)
Оказывается, если имеются два каких-либо решения:
xi=ji(t) (i=1, 2, ..., n), xi=ci(t) (i=1, 2, ..., n) (10)
системы (1), удовлетворяющих условиям
ji(t(0))=ci(t(0))=xi(0) (i=1, 2, ..., n), (11)
причем каждое решение определено на своем собственном интервале значений переменного t, содержащем точку t0, то эти решения совпадают всюду, где они оба определены.
Теорема 2. Непрерывная зависимость решения от параметров [2].
Рассматривается нормальная система уравнений:
d(xi)/d(t)=fi(t, x1, ..., xn, m1, ..., mk) (i=1, 2, ..., n), (12)
правые части которых зависят от параметров mk, ..., mk и определены в некотором открытом множестве D пространства R переменных t, x1, ..., xn, m1, ..., mk.
Предполагается, что правые части системы (12) и их частные производные dfi/dxj, где i, j=1, 2, ..., n, по переменным x1, ..., xn являются в D непрерывными функциями совокупности всех переменных.
Пусть
xi=ji(t) (i=1, 2, ..., n) – (13)
решение системы уравнений (12), определенное на интервале r1<t<r2, и
xi=yi(t) (i=1, 2, ..., n) – (14)
решение той же системы уравнений (12), определенное на интервале s1<t<s2. Говорят, что решение
(14) является продолжением решения (13), если интервал s1<t<s2 содержит интервал r1<t<r2 и решение (13) совпадает с решением (14) на интервале r1<t<r2. В частности, будем считать, что решение (14) является продолжением решения (13) и в том случае, когда оба решения полностью совпадают, то есть s1=r1, s2=r2. Решение (14) назовем непродолжаемым, если не существует никакого отличного от него решения, являющегося его продолжением.
Точку пространства R обозначим через (t, x1, ..., xn, m1, ..., mk). Зафиксируем начальные значения
t(0), x1(0), ..., xn(0) и обозначим через M совокупность всех таких m, что точка (t(0), x1(0), ..., xn(0), m1, ..., mk) принадлежит множеству D. Очевидно, что M является открытым множеством в пространстве переменных m1, ..., mk. Каждой точке m множества M соответствует непродолжаемое решение j(t, m1, ..., mk) с начальными значениями t(0), x1(0), ..., xn(0) уравнений (12), определенное на интервале m1(m)<t<m2(m), который, очевидно, может зависеть от m, что и выражено в обозначениях. Множество T всех пар (t),
(m1, ..., mk), для которых функция j(t, m1, ..., mk) определена, описывается, очевидно, условиями: точка
m1, ..., mk принадлежит множеству M, а число t удовлетворяет при этом неравенствам m1(m)<t<m2(m).
Множество T всех пар (t), (m1, ..., mk), на которых определены функции ji(t, m1, ..., mk) (i=1, ..., n), являющиеся при каждом фиксированном m1, ..., mk непродолжаемыми решениями уравнений (12) с начальными значениями t(0), x1(0), ..., xn(0), представляет собой открытое множество пространства переменных t,
m1, ..., mk. Оказывается, что функция ji(t, m1, ..., mk) (i=1, ..., n) есть непрерывная функция пары переменных t, (m1, ..., mk) на множестве T.
Теорема 3. Непрерывная зависимость решения от начальных значений [2].
Рассматривается нормальная система уравнений (1), правые части которой определены и их частные производные dfi dxj (i, j=1, 2, ..., n) по переменным x1, ..., xn являются в D непрерывными функциями совокупности всех переменных.
Каждой точке (t, t, x1, ..., xn) множества D соответствует непродолжаемое решение ji(t, t, x1, ..., xn)
системы (1) с начальными значениями t(0)=t, x1(0)=x1, ..., xn(0)=xn, определенное на интервале
m1(t, x1, ..., xn)<t<m2(t, x1, ..., xn), который зависит от начальных значений t, x1, ..., xn.
Множество D всех точек (t, t, x1, ..., xn), на которых определена функция ji(t, t, x1, ..., xn), где i=1, ..., n, являющиеся непродолжаемым решением системы (1) с начальными значениями t, x1, ..., xn, есть открытое множество в пространстве переменных t, t, x1, ..., xn. Функции ji(t, t, x1, ..., xn), где i=1, ..., n, непрерывны по совокупности всех своих аргументов на множестве D.
Теорема 4. Теоремы 2 и 3 могут быть объединены в одну обобщенную теорему [2].
Пусть x=j(t, t, x, m) (t, x, m – векторы; j – вектор-функция) – непродолжаемые решения системы (1) с начальными значениями t, x. Тогда функция j(t, t, x, m) определена на некотором открытом множестве пространства переменных t, t, x, m и непрерывна на нем.
Следствия предыдущих теорем.
Прежде чем перейти к следствиям, отметим, что x, x, m – векторы, j – вектор-функция, как было указано при записи теоремы 4.
Если решение j(t, m) системы (1) с начальными значениями t(0), x(0) при m=m* определено на отрезке r1£t£r2, содержащем t(0) (это означает, что отрезок r1£t£r2 содержит в интервале определения решение j(t, m)), то существует такое положительное число r, что при |m-m*|£r непродолжаемое решение j(t, m) с начальными условиями t0, x0 также определено на отрезке r1£t£r2. Для всякого положительного e найдется такое положительное d<r, что при r1£t£r2, |m-m*|£d имеем |j(t, m)-j(t, m*)|<e.
Если решение j(t, x)=(t, t(0), x) системы (4) с начальными значениями t(0), x при x=x(0) определено на отрезке r1£t£r2, содержащем t(0), то существует такое положительное число r, что при |x-x(0)|£r непродолжаемое решение j(t, x) также определено на отрезке r1£t£r2. Для всякого положительного e найдется такое положительное d<r, что при r1£t£r2 |x-x(0)|£d имеем: |j(t, x)-j(t, x(0))|<e.
Модели идеального вытеснения
Теорема 5. Существование и единственность решений линейных дифференциальных уравнений в частных производных в классе аналитических функций (теорема Коши–Ковалевской) [3, 4].
Введем обозначения.
Точку пространства Rn+1 будем обозначать через (x, t)=(x1, ..., xn, t), а точку, принадлежащую Rn, через x=(x1, ..., xn). Пусть
(15)
– оператор, представленный в нормальной форме (производная нулевого порядка равна самой функции).
Предположим, что коэффициенты оператора L определены в окрестности U начала координат в пространстве переменных (x, t) и являются аналитическими функциями. Пусть функция f также аналитична в U. Пусть вектор y начальных данных является аналитическим в некоторой окрестности начала координат x-пространства. Тогда существует окрестность W начала координат и единственная аналитическая функция u(x,t), определенная в W, для которой
Lu = f, (x, t) Î W,
(d/dt)ju(x,0)=uj(x), xÎWÇ{t=0} (j=0, 1, ..., m-1). (16)
Замечание.
Вопрос об единственности решения задачи Коши для нелинейных уравнений, если аналитические условия Коши задаются на аналитической поверхности, нигде не имеющей характеристических направлений, легко сводится к вопросу об единственности решения задачи Коши для линейных уравнений с достаточно гладкими, но необязательно аналитическими коэффициентами.
Теорема 6. Непрерывная зависимость решения от начальных данных [3, 4].
Пусть F – пространство функций в Rn, непрерывно дифференцируемых m раз; последовательности функций и их производные до порядка m включительно сходятся равномерно к нулю на любом компактном (замкнутом ограниченном) множестве.
Предположим, что все коэффициенты оператора (16) аналитические и задача Коши для оператора L локально разрешима в начале координат в классе F. Тогда решение задачи Коши непрерывно зависит от начальных данных (приведена неполная формулировка теоремы).
Необходимо отметить, что теорема Коши–Ковалевской доказана для систем дифференциальных уравнений в частных производных при одном ограничении, которое накладывается на правую часть уравнения: это требование аналитичности функций, которое отсутствует в аналогичных теоремах для обыкновенных дифференциальных уравнений.
Теоремы, посвященные обыкновенным дифференциальным уравнениям, содержат более общие утверждения, поэтому теорема Коши–Ковалевской была выделена с соответствующей оговоркой относительно аналитичности правой части для систем дифференциальных уравнений в частных производных.
В работе для обоснования возможности построения дискретных моделей рассматриваются детерминированные функциональные операторы.
Основные математические свойства уравнений, входящих в функциональные операторы, – существование и единственность решений, а также непрерывная зависимость решений от параметров и от начальных значений, что позволяет сделать вывод о непрерывности области существования функциональных операторов для рабочих режимов.
Дискретные автоматные модели непрерывных химико-технологических систем.
Метод разделения состояний
На основе свойств непрерывных технологических операторов можно показать возможность построения дискретных автоматных моделей.
Определение автомата. Наиболее общее описание детерминированного автомата можно задать в следующем виде [5, 6]:
Adet=<X, A, ¡, A(0), F, Y>, (17)
где X={x1, ..., xn} – входной алфавит (n – мощность входного алфавита); ¡={u1, ..., um} – выходной алфавит (m – мощность выходного алфавита); A={a1, ..., al} – алфавит состояний ( l – мощность алфавита состояний); F=F(xs, ai(k-1), aj(k)) – функция перехода из одного из возможных состояний на k-м шаге ai(k-1)
в aj(k) (ai(k-1), aj(k)ÎA) при появлении какого-либо символа xs(xsÎX); Y=Y(xs, ai(k-1), uq) – функция выхода автомата, который задает соответствие между состоянием автомата ai(k-1), поступившим символом на вход xs и выходным символом uq (uqΡ).
В данной работе введение алфавитов входа, состояния и выхода функционального оператора Ti осуществляется на основе выделения непересекаемых областей в пространствах qi, xi и yi, которым ставятся в соответствие символы соответствующих алфавитов. Построение алфавитов должно быть проведено таким образом, чтобы существовало однозначное отображение множества пар (x, a), где x Î X и aÎ A, в множества A и ¡.
Рассмотрим обобщенное описание процедуры построения алфавитов для рассматриваемых классов функциональных операторов, при этом необходимо учесть, что практически одновременно с выделением элементов алфавита строится и таблица автоматных соответствий.
Для некоторого упрощения рассуждений рассмотрение будем вести для алфавитов входа и состояния.
Разделим пространство состояний xi функционального оператора Ti на две произвольные области, не имеющие общих точек (условно назовем их первая ai(1) и вторая ai(2)), то есть тем самым выделим два символа алфавита и определим, какая часть пространства входных воздействий qi индуцирует переход, предположим, из первой ai(1) во вторую ai(2).
На данном шаге это позволит нам разделить пространство qi на две непересекающиеся области xi(1, 1) и xi(1, 2). xi(1, 1), предположим, не дает перехода из первой области состояний во вторую, а xi(1, 2) дает такой переход.
Осуществляя зондаж второй области состояний ai(2), определим также xi(2, 1), xi(2, 2). Области qi(1)=xi(1, 1)Èxi(1, 2) и qi(2)=xi(2, 1)Èxi(2, 2) являются равными (равенство областей соответствует их геометрическому и пространственному совпадению).
Основное требование, которое при выделении областей алфавитов входа должно выполняться, заключается в следующем: необходимо, чтобы при заданной области начального элемента алфавита состояния и заданной области данного элемента алфавита входа переход осуществлялся только в область одного элемента алфавита состояний. Данное требование вытекает из свойств автоматных отображений [7].
Если область, соответствующая определенному элементу алфавита входа, индуцирует переход не в одну, а в несколько областей, соответствующих различным элементам алфавита состояний, возникает неопределенность перехода. В этом случае необходимо данную область алфавита входа разделить таким образом, чтобы выполнялось основное требование выделения областей алфавита.
Рассмотрим множество определенных ранее областей {xi(1, 1), xi(1, 2), xi(2, 1), xi(2, 2)}. Для некоторого упрощения записей введем сквозную нумерацию элементов множества {xI(1), xi(2), xi(3), xi(4)}. Если каждый элемент множества есть область пространства qi, то, исходя из его геометрических свойств, можно написать выражение:
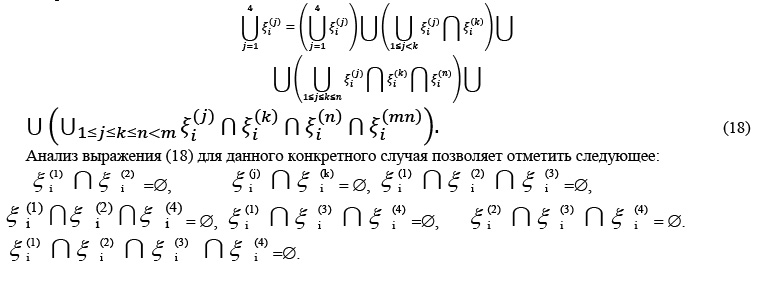

Таким образом, если наложить qi1 и qi2, то возможны несколько вариантов разделения пространства qi, например
xi(1) = xi(3), xi(2) = xi(4), (20)
xi(1) ¹ xi(3), xi(2) ¹ xi(4). (21)
В первом случае появляются два элемента алфавита входа (xi(1), xi(2)), во втором – ряд элементов, количество которых определяется конфигурацией границ областей. Для простейшего случая, рассмотренного выше, – (xi(1), xi*, xi(2)).
Анализ формул (18) и (19) показывает, что при наложении областей возможно несколько вариантов объемного раскроя на элементы алфавита:
– одна область поглощает другую, в этом случае как поглощаемая область, так и оставшаяся часть поглощающей области выделяются как отдельные элементы алфавита, например, xi(1) Ç xi(3) выделяет два элемента алфавита, которые условно можно назвать xi(1) и xi*;
– две области совпадают, в этом случае выделяется отдельный элемент алфавита, соответствующий данным областям;
– при пересечении двух областей выделяются три элемента алфавита, например xi(2)Çxi(3) выделяет xi(2) \ xi(*), xi* и xi(3) \ xi* .
Теперь разделим пространство состояний xi технологического оператора Ti на n произвольных областей, не имеющих общих точек (назовем их ai(1), ai(2), ..., ai(n)), и определим, для какой части пространства входных воздействий qi возможен переход из ai(j) в ai(k) (j, k = 1, 2, ..., n).
Это позволит пространство qi для каждого ai(j) разделить также на непересекающиеся области xi(j,1), ..., xi(j,n):

– общее число элементов алфавита входа при заданном числе элементов алфавита состояний конечно, их максимальное количество может быть оценено следующим образом:
.
Выше было рассмотрено построение алфавита входных воздействий при заданном алфавите состояний, однако в общем случае необходимо также рассматривать пересечения, которые могут возникать при учете алфавита выхода.
К оценке количества элементов алфавита входа в формуле (22) необходимо учесть пересечения, которые будут возникать в результате построения областей элементов алфавита входа при заданных наборах алфавитов состояний и выхода. При этом общий вид формулы (22) не изменится и, естественно, количество элементов алфавита возрастет.
При таком подходе к построению алфавитов детерминированного автомата в зависимости от выбора алфавитов состояния и выхода могут быть получены различные алфавиты входных воздействий, то есть число алфавитов бесконечно.
Метод разделения состояний
Абстрагируясь от физического существа явлений, процесс функционирования любой химико-технологической системы (ХТС) можно рассматривать как последовательную смену ее состояний в некотором интервале времени (t0, tk). Состояние системы в каждый момент времени t из этого интервала характеризуется набором переменных x1, x2, ..., xn.
Рассмотрим описание метода разделения состояний для линейных объектов.
Дифференциальные уравнения, описывающие поведение линейных систем, в общем виде можно записать следующим образом:
dx/dt = Аx + b. (24)
Здесь x – вектор переменных состояния, чаще всего это концентрация вещества или температура; А – матрица коэффициентов, которая характеризует выходные потоки вещества или энергии ХТС; b – вектор, характеризующий входные потоки веществ или энергии; t – время.
Рассмотрение метода разделения состояний начнем с рассмотрения статических режимов работы. Очевидно, что множество точек, соответствующее определенному статическому режиму, определяется правой частью системы (24):
Аx + b = 0. (25)
Как известно, для технологических аппаратов существуют диапазоны параметров входных и выходных потоков, которые определяют элементы матрицы А и координаты вектора b, а также диапазоны переменных состояния, задающие режимы работы технологического процесса. Всегда существует система ограничений по переменным состояния, выделяющих тот или иной режим вида
xik(min) < xi < xik(мах), (i=1, I; k=1, Ki) (26)
или в векторной форме: xk(min) < x < xk(мах).
Здесь i – номер переменной состояния; k – номер технологического режима работы i-й переменной.
Наличие таких технологических ограничений на переменные состояний позволяет с какой угодно степенью дифференциации перечислять на основе чисто комбинаторного перебора возможные непересекаемые области существования переменных состояний или элементы алфавита состояний ai.
Аналогично и для коэффициентов матрицы А и координат вектора b могут быть определены минимально и максимально допустимые значения, хотя для конкретных вариантов расчета их можно брать постоянными величинами:
aij(min)< aij < aij(мах), (i=1, I; j=1, I), (27)
bi(min) < bi < bi(мах), (i=1, I). (28)
Обозначим область существования коэффициентов матрицы А и координат вектора b, определяемую неравенствами (27) и (28), через X.
Система (25) определяет уравнение гиперплоскости относительно вектора x. Если рассматривать координаты x как константы, а элементы матрицы А и вектора b как переменные, принадлежащие области ограничений, задаваемой неравенствами (27) и (28), то в результате получим, что система уравнений (25) будет определять также уравнение гиперплоскости, но уже относительно элементов матрицы А и координат вектора b.
Введем матрицу Xq, которая формируется из элементов векторов xq(min) и xq(max), а также из коэффициентов при координатах вектора b, и образуем вектор переменных z, в который входят все элементы матрицы А и вектора b.
Матрица X для произвольного aq-го элемента алфавита будет иметь вид:
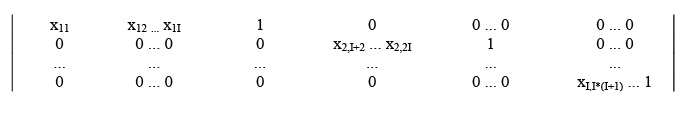
Здесь x11, x2, I+2, ..., xI, (I-1)(I+1)=x1 и т.д., xI, I (I+1)=1. Матрица X будет иметь размерность IxI (I+1).
Вектор переменных zq aq-го режима запишется как z = (z1, z2, ..., zL), где соответствие элементов будет следующее: z1 = a11, z2 = a12, ... , zI = a1I, zI+1 = b1 и т.д. Размерность вектора L=I (I+1).
В [8] показано, что на основе вышеприведенных неравенств (26) и системы (25) можно получить системы линейных ограничений (27) и (28), выделяющие в области X, области элементов матрицы А и вектора b или вектора z, принадлежащие некоторому элементу алфавита входа, области xq, соотносящейся с некоторой областью элемента алфавита состояний aq. Естественно, при этом необходимо учитывать следующую систему ограничений:
Xq< z < 0, (29)
Xq> z > 0. (30)
Здесь Xq<, Xq> – матрицы Xq, образованные нижней и верхней границами для q-го режима работы по координатам переменных состояния x на основе ограничений (31) aq элемента алфавита состояний.
Правила для образования матриц Xq< и Xq> для q-го режима (здесь zh соответствует aij, где i=entire(h/(I+1)) +1 и j=h-i; entire(s) – функция выделения целой части s, p = j - entire(j / (I+1)), таковы:

Системы ограничений (27) и (28) можно назвать тривиальными. Их необходимо рассматривать совместно с системами (29) и (30) для каждого q-го режима. В соответствии с введенными обозначениями запишем общий вид этих ограничений в матричной форме:
(X*, zq) > g(min) (i =1, ..., L), (31)
(X*, zq) < g(max) (i =1, ..., L). (32)
Здесь вектор g(min) образован минимальными значениями элементов матрицы А и вектора b, а g(max) – максимальными, аналогично порядку формирования вектора z, X*– единичная матрица.
В работе [8] рассмотрен подход, позволяющий получать дискретные модели для динамических и квазистатических процессов, которые могут быть отнесены к классу комбинационных автоматов.
Дискретный вариант системы уравнений (24) может быть записан следующим образом:
x(k+1) = А(k)x(k) + b(k), (33)
где k – текущий номер интервала квантования (k=0, 1, 2, ...). На переменные состояния и на коэффициенты системы (24) могут быть наложены ограничения (26)–(28).
Данная система может быть подвергнута преобразованиям, в результате которых получится следующая система ограничений:
(Xiq<(k), z(k)) < Dx(k+1), (i =1, ..., I), (34)
(Xiq>(k), z(k)) > Dx(k+1), (i =1, ..., I). (35)
Ограничения (27), (28) остаются без изменения для дискретных моделей квазистатических и динамических режимов.
Неравенства (34), (35) играют важную роль для организации контроля за состоянием технологических процессов, на основе которых осуществляется классификация состояний ХТС. Кроме того, соотношения (34), (35) позволяют прогнозировать возникновение постепенных отказов, являющихся результатом ухудшения свойств веществ, участвующих в ХТП (например, ухудшение свойств катализатора в реакторе), свойств аппаратов (образование накипи на поверхности теплообменника) и т.д., которые приводят к нарушению ограничений (34), (34) и тем самым указывают на появление неполадок в технологической системе.
Приведенная выше процедура применима и для решения другой задачи – определения диапазонов работы переменных состояния при заданных ограничениях на коэффициенты дифференциальных уравнений, то есть должна рассматривать ограничения (27) и (28) не для всего возможного диапазона работы. Необходимо разбить его на интервалы (как это было сделано для переменных состояния x) и получить новые ограничения относительно теперь уже x.
Это позволит либо прогнозировать новый режим работы технологического процесса, который появляется при изменении входных возмущений, либо диагностировать состояние оборудования или систем управления при появлении нарушений в работе технологического процесса.
Метод разделения состояний на основе использования методов линеаризации может быть применен и для нелинейных объектов химической технологии. Использование линейной аппроксимации определяется тем фактом, что в объектах управления уже существуют определенные области переменных состояния, в которых нелинейные зависимости могут быть с достаточной степенью точности заменены линейными и которые в то же время определяют различные режимы работы технологических систем, установленные на этапах предпроектных и проектных разработок, а также в условиях их эксплуатации.
Дифференциальные уравнения в частных производных используются в моделях идеального вытеснения и диффузионных одно- и двухпараметрических моделях. Особенность данных моделей в том, что их можно с достаточной степенью точности представить в виде ячеечных моделей, основой которых является представление об идеальном перемешивании в пределах ячеек, расположенных последовательно. Это дает возможность применить уже описанные методики для построения дискретных моделей ХТП данного класса.
Рассмотренный выше подход к построению математических моделей ХТС позволяет проводить построение дискретных моделей и для аппаратов, описываемых комбинированными математическими моделями.
Таким образом, рассмотрена методология построения дискретных моделей непрерывных ХТП, которые могут быть применены для целей диагностики состояний технологических процессов и управления их безопасным функционированием.
Построение дискретной модели непрерывной ХТС, которая позволяет отнести мгновенное состояние технологического процесса к определенному классу состояний, является первым этапом построения автоматных моделей ХТС, основное назначение которых - моделирование событийных процессов, происходящих в объекте управления, и отражение причинно-следственных связей, существующих в самих технологических процессах, в их оборудовании и системах управления.
Большой класс объектов химической технологии описывается нелинейными обыкновенными дифференциальными уравнениями:
dx/dt = Ax + b + F(x). (36)
Здесь x, A и b имеют то же смысловое содержание, что и для линейных систем.
Наибольшие затруднения при исследовании и анализе таких систем вызывает F(x), которая характеризует нелинейные явления взаимодействия веществ и обмен энергией в ХТС во время выполнения технологических операций, ее построение осуществляется на основе фундаментальных физико-химических законов.
Сложность и труднодоступность исследования F(x) довольно часто приводят к необходимости строить аппроксимационные зависимости разного вида данного члена уравнения. Одним из методов аппроксимации, к которому часто прибегают в практических и теоретических задачах моделирования, является представление F(x) в виде ряда Тейлора:
(37)
При линейной аппроксимации берутся члены ряда не выше первого порядка и F(x) должна быть дифференцируема.
Полезность использования линейной аппроксимации в данной работе определяется и тем фактом, что при управлении ХТС уже существуют определенные области переменных состояния, в которых нелинейные зависимости с достаточной степенью точности могут быть заменены линейными и которые в то же время определяют различные режимы работы технологических систем, установленные на этапах предпроектных и проектных разработок, а также в условиях их эксплуатации.
Поэтому будет естественным расширение вышеизложенного метода построения дискретных автоматных моделей для линейных систем на нелинейные системы. Основное ограничение такого подхода – требования, накладываемые на точность используемой модели.
В связи с этим в некоторых режимах работы может возникнуть необходимость задания нескольких линеаризованных F(x). Это приведет к выделению отдельных зон линейности в каком-либо из режимов, которые, в свою очередь, могут быть представлены как отдельные режимы. При этом система ограничений, выделяющая отдельные состояния, остается прежней, хотя методика их построения претерпевает некоторые изменения, которые в основном связаны с определением областей линейной аппроксимации.
Если для описания ХТП используются нелинейные уравнения более общего вида dx/dt=F(t, x), то и они могут быть линеаризованы для различных режимов работы в соответствии с требованиями точности линеаризации на основе ряда Тейлора.
Таким образом, последовательность действий, которую необходимо выполнить для разделения состояний технологических режимов объектов, описываемых нелинейными моделями, будет следующая:
исследование математической модели нелинейного объекта с целью выделения зон линейности;
построение линейных аппроксимирующих зависимостей в соответствии с требованиями точности;
задание систем ограничений;
построение непересекаемых областей существования переменных состояния aq на основе комбинаторного перебора;
формирование системы ограничений для каждого xq либо для квазистатических или динамических режимов работы.
Химико-технологические системы, описываемые дифференциальными уравнениями
в частных производных
Дифференциальные уравнения в частных производных используются в моделях идеального вытеснения и диффузионных одно- и двухпараметрических моделях:
¶ x/dt = W¶ x/¶ z + F(x), (38)
¶ x/dt = W¶ x/¶ z + DL ¶ 2x/¶ z2 + F(x), (39)
¶ x/¶ t = W¶ x/¶ z + DL¶ 2x/¶ z2 + DR¶ (R¶ x/¶ R)/¶ R + F(x). (40)
Здесь x, t имеют тот же смысл, что и в вышеприведенных уравнениях; W – матрица линейных скоростей потоков; z – координата; DL – матрица коэффициентов продольного перемешивания или коэффициентов турбулентной диффузии; DR – матрица коэффициентов, которые характеризуют радиальное перемешивание; R, L – определяющие линейные размеры аппарата, в котором происходит технологический процесс.
Необходимо отметить, что вышеприведенные системы уравнений построены при определенных
допущениях и в каждом конкретном случае возможны некоторые отклонения, хотя их общий вид соответствует системам (38)–(40). Данные типы моделей часто встречаются в практике моделирования технологических процессов ХТС и создают наибольшие трудности при исследовании и анализе технологических процессов.
Отличительная особенность моделей, построенных на основе дифференциальных уравнений
(38)–(40), заключается в том, что их можно с достаточной степенью точности представить в виде ячеечных моделей, основой которых является представление об идеальном перемешивании в пределах ячеек, расположенных последовательно.
Другими словами, можно перейти от описания в виде дифференциальных уравнений в частных производных к обыкновенным дифференциальным уравнениям, линейным или нелинейным (36), в зависимости от свойств объекта. Это соответствует замене одного аппарата несколькими последовательно
соединенными аппаратами. Количество ячеек или последовательно соединенных аппаратов в гипотетической модели определяется требованием точности, и в литературных источниках, посвященных моделированию ХТП, приводятся оценки, позволяющие определить их число. Связь между переменными
состояния на выходе аппарата и входными переменными может быть получена на основе матричных преобразований, которые будут рассмотрены ниже.
Таким образом, системы (38)–(40) можно заменить системами обыкновенных линейных или нелинейных дифференциальных уравнений. Это дает возможность применить вышеописанные методики для
построения дискретных автоматных моделей ХТП. При этом необходимо провести дополнительное исследование объекта для определения числа ячеек в соответствии с необходимой точностью выполнения вычислений, а также с целью согласования режимов работы по переменным состояния и входным и выходным потокам ячеечной модели.
Вышерассмотренные классы математических моделей ХТС позволяют проводить построение дискретных моделей и для аппаратов, описываемых комбинированными математическими моделями, которые являются производными от классов моделей идеального смешения, вытеснения и диффузионных моделей.
Алгоритм построения ограничений на коэффициенты дискретных моделей
Постановка задачи. При заданных x(min) и x(мах) найти диапазоны изменения коэффициентов системы (aij(min) и aij(мах) (i=1, I; j=1, I), а также bi(min) и bi(мах) (i=1, I) таким образом, чтобы была справедлива система ограничений (29), (30) или (34), (35).
Решение. Предлагаемый метод решения осуществляет поиск ограничений перебором с переменным шагом. Для этого мы задаем начальное положение системы и определяем минимальное значение шага. Поиск проходит в два этапа: сначала ищется матрица максимальных значений коэффициентов, а затем минимальных.
Рассмотрим алгоритм поиска минимальных значений. Максимальные значения ищутся аналогично.
Матрице A(min) присваивается начальное значение, определяемое заданными коэффициентами. Затем идет последовательное изменение (уменьшение) каждого коэффициента на величину шага, определяемую соответствующим значением матрицы шагов dA (для каждого коэффициента системы рассчитывается свой шаг, таким образом существенно повышается эффективность алгоритма). После изменения каждого коэффициента делается проверка, не вышло ли решение за пределы искомого диапазона (о том, как делается эта проверка, будет сказано ниже). Если проверка не дала положительного результата, выполняется откат – коэффициенту присваивается исходное значение. Далее вычисляется новый шаг для текущего коэффициента – увеличение вдвое, если проверка была пройдена успешно, или уменьшение вдвое – в противном случае. Новое значение шага записывается в матрицу dA. В случае, если шаг оказался меньше заданного минимального значения, текущий коэффициент более не меняется.
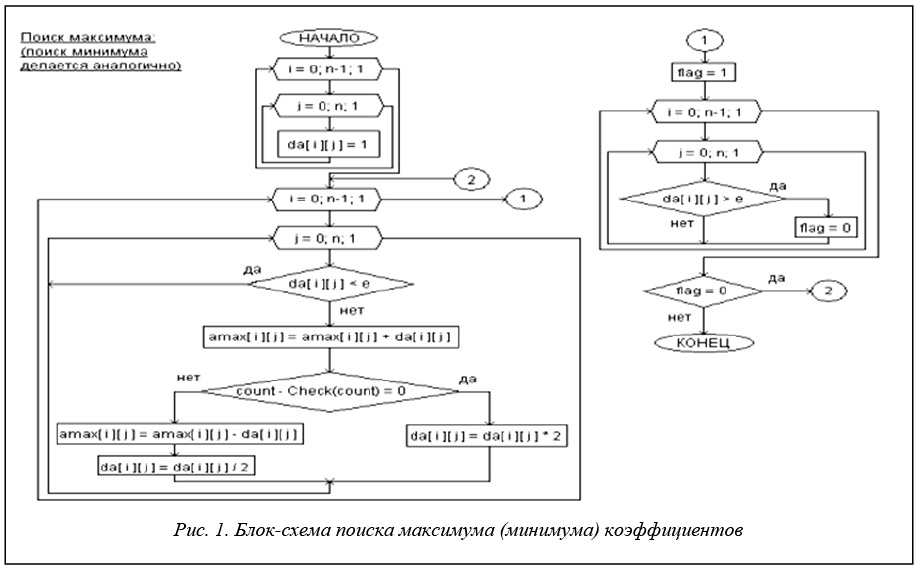
После того как будет сделан проход по всей матрице A(min), программа анализирует матрицу шагов и смотрит, остались ли элементы, не достигшие предела. Если таковые найдены, процесс повторяется для этих элементов. Если же все элементы достигли предела, программа переходит к следующему этапу.
Проверка на принадлежность решения Аx+b=0 диапазону xk(min) < x < <xk(мах) коэффициентов для матрицы A и вектора b, рассчитанных на очередной итерации, производится следующим образом. Много раз случайным образом генерируется система коэффициентов матрицы A и вектора b из текущего диапазона. Если в каждом случае решения системы выполняются ограничения (29), (30) или (34), (35), проверка считается удачно пройденной. Если же хотя бы при одной из попыток был выход решений за допустимый диапазон, проверка завершается неудачно. При достаточно большом количестве испытаний надежность составляет 95–97 %, что во многих случаях достаточно для практических расчетов.
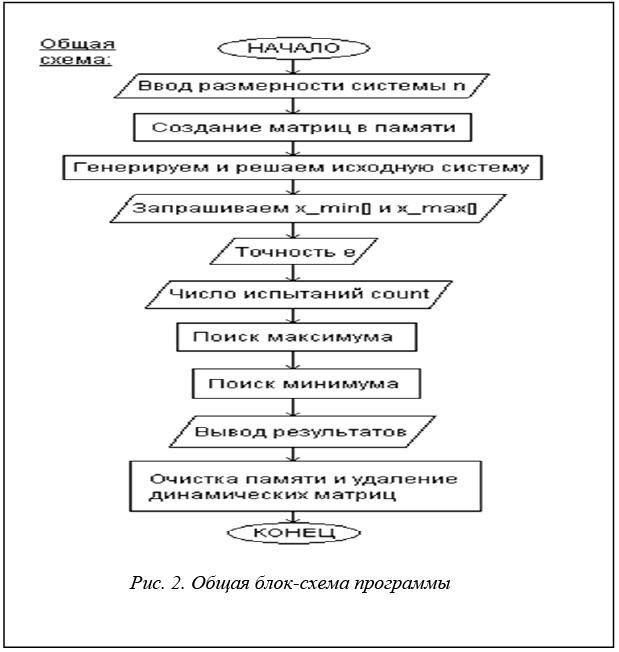
Алгоритм
Приведенный выше метод решения может быть записан в виде следующего алгоритма.
Увеличиваем (при поиске минимума уменьшаем) значение очередного коэффициента на соответствующее значение из матрицы da.
Делаем статистическую проверку в функции check().
Если проверка завершилась неудачно, возвращаем коэффициенту исходное значение, а соответствующий элемент из матрицы dA уменьшаем вдвое.
Если же проверка прошла успешно, увеличиваем шаг изменения (элемент матрицы dA) вдвое.
В случае, если значение соответствующего элемента матрицы dA стало меньше заданного предела точности, считаем, что граница изменения данного коэффициента системы достигнута, и в дальнейшем пропускаем этот коэффициент.
Переходим к следующему коэффициенту.
Как только все коэффициенты достигли предельных значений, переходим к следующему этапу.
Блок-схема, описывающая программу, приведена на рисунке 1.
Построение дискретных моделей на основе теории нечетких множеств
Рассмотрим методику построения дискретных моделей на основе теории нечетких множеств. Возникновение подхода на основе нечетких множеств основывается на том факте, что представление о состоянии объекта для каждого человека является размытым, и в данном случае построение модели основано на том, что не существует четкой границы между переходами из состояния в состояние.
Например, если границей режимов считать значение температуры T*, то изменение температуры относительно этой границы не всегда может означать переход к другому режиму работы технологического процесса, то есть существует некоторый диапазон – диапазон неопределенности, которому принадлежит T*. Величина диапазона определяется точностью контролирующих приборов, характером протекания технологического процесса, а также первопричинами, приведшими к такому изменению переменной состояния.
При использовании нечетких множеств состояние объекта диагностирования оценивается также по значениям переменных состояния, описывающих данный объект. Но теперь определение состояния объекта управления осуществляется на основе применения оценки, которая интерпретируется как степень нечеткого равенства текущего состояния некоторому эталонному состоянию. Понятие нечеткого равенства рассмотрено далее.
Каждый элемент алфавита состояний определяется заданием значений функций принадлежности переменных состояния, типичных для данного элемента алфавита, которые можно назвать эталонными для данного элемента алфавита состояний A. Для задания нечеткого множества эталонных состояний используются ограничения, на основе которых формируется множество A.
В результате такого разбиения получаем нечетко определенное множество элементов алфавита состояний.
Каждой переменной состояний xi (iÎI={1, 2, ..., р}) ставится в соответствие лингвистическая
переменная, которая описывается как тройка <уi, Тi, Di>, где уi – название переменной состояния; Тi = ={Т1i, Т2i, ..., ТMii} – терм-множество лингвистической переменной уi, каждый элемент которого соответствует отдельному интервалу переменной состояния xi; Mi – число значений лингвистической переменной или число интервалов; Di – базовое множество лингвистической переменной уi. Каждому интервалу переменной состояния, за которым закрепляется элемент терм-множества, ставится в соответствие своя функция принадлежности (рис. 3).

Набор значений переменных состояния, описывающих состояние объекта в некоторый момент времени, назовем ситуацией. При описании типовых ситуаций эксперту удобнее пользоваться словесными значениями признаков, представляющих собой значения соответствующих лингвистических переменных.
Для описания термов Тij (j Î L = {1, 2, ..., Mi}), соответствующих значениям уi, используются нечеткие переменные <Тij, Di, %C ij>, то есть Тij описывается нечетким множеством %C ij в базовом множестве Di:
%C ij = {<m %C i j (d)/d>}, d Î Di,
где m %C i j (d) – степень принадлежности элемента d нечеткому множеству %C ij.
Нечеткой ситуацией %S называется нечеткое множество второго уровня:
%S ij = {<m S (yj)/ yj >}, yj Î Yi,
где m S (yj) = {<m m s (yj) (Тij)/ Тij >}.
Отличительная особенность построения модели объекта управления на основе нечетких множеств состоит в том, что моделируется не сам объект, а человек-оператор в процессе управления объектом, который при данной входной ситуации принимает решения по системе продукций, определяет возможные причины ненормальной работы объекта и способы их устранения. Продукционная система, моделирующая работу оператора, ставит в соответствие каждой ситуации %Si из определенного набора ситуаций Ss, характеризующего все возможные состояния объекта диагностирования, некоторое управляющее решение Ri.
Ситуации, входящие в набор Ss, как было определено выше, называются эталонными. В отличие от набора ТSs ={ТS1, ТS2 , ..., ТSn} текущих ситуаций набор Ss ={%S1, %S2 , ..., %Sn} (n £ N) эталонных ситуаций не содержит нечетко равных при заданном пороге равенства ситуаций.
Входная нечеткая ситуация ТS0 сравнивается с эталонными ситуациями %SiÎSs, и определяется эталонная нечеткая ситуация, в некотором смысле наиболее близкая входной нечеткой ситуации. Предполагается, что множество Ss полно. Это предположение действительно выполняется, так как множество эталонных ситуаций строится на основе комбинаторного перебора всех возможных интервалов переменных состояний. Таким образом, ситуация %Si существует для любой входной ситуации S0. По решающей таблице для этой эталонной ситуации определяется управляющее решение.
В качестве меры близости между ситуациями обычно рассматриваются два критерия: степень нечеткого включения и степень нечеткого равенства.
Понятие степени нечеткого включения ситуации базируется на определении степени включения нечетких множеств. Пусть
%S i = { <m Si (y)/ y > }, %S j = { <m Sj (y)/ y > }, y Î Y
– некоторые ситуации. Степень включения ситуации %Si в ситуацию %Sj обозначается n(%Si , %Sj) и определяется выражением
n(%Si , %Sj) = & n( m Si (yp), m Sj (yp)).
yp Î Y
Здесь величина n( m Si (yp), m Sj (yp)) определяется по формуле
и является степенью включения нечеткого множества mSi (yp) в нечеткое множество mS j(yp).
Для ограничения возможных вариантов альтернатив, возникающих при диагностике ХТП, будем считать, что ситуация %Si нечетко включается в %Sj, %SiÍ%Sj, если степень включения %Si в %Sj не меньше некоторого порога включения tincÎ [0,6; 1], определяемого условиями управления, то есть n(%Si, %Sj) ³ tinc. Другими словами, ситуация %Si нечетко включается в ситуацию %Sj, если нечеткие значения признаков ситуации %Si нечетко включаются в нечеткие значения соответствующих признаков ситуации %Sj. Фиксация порога включения в некоторой точке интервала [0,6; 1] зависит от особенностей объекта управления, требований к качеству управляющих решений и т.д. Повышение нижней границы интервала с 0,5 до 0,6 вызвано необходимостью повышения степени достоверности при диагностике ХТП.
Если множество текущих ситуаций S содержит такие ситуации %Si и %Sj (i, j Î K = {1, 2, ..., N}, i ¹ j), что %Si нечетко включается в %Sj, а %Sj нечетко включается в %Si, то ситуации %Si и %Sj нужно воспринимать как одну ситуацию. Это означает, что при данном пороге включения tinc ситуации %Si и %Sj примерно одинаковы. Такое сходство ситуаций называется нечетким равенством, при этом степень нечеткого равенства
m(%Si , %Sj) = n(%Si , %Sj) & n(%Sj , %Si).
Считается, что ситуации %Si и %Sj нечетко равны, если m(%Si , %Sj) ³ tinc, где tinc Î [0,6; 1] – порог нечеткого равенства.
Необходимо отметить, что степень нечеткого равенства характеризует возможные альтернативы, которые возникают при проведении поиска причин возникновения нарушений технологических режимов работы ХТП. Количественная оценка m(%Si, %Sj) позволяет определить порядок выполнения диагностических операций в соответствии с возможным множеством альтернатив.
Рассмотрим пример использования дискретной модели, построенной на основе применения нечетких множеств. Необходимо отметить, что в данном случае построение дискретной модели процесса не соответствует вышеизложенной методике и базируется в большей степени на экспертных оценках и реальной информации, получаемой с объекта управления. Это замечание относится к выбору переменных состояния. В данной дискретной модели показаны образование элементов алфавита и механизм принятия решений.
На основе данных технологического регламента типового производства слабой азотной кислоты по схеме УКЛ-7-71/76 [9] были выделены следующие параметры ХТП, характеризующие работу контактного аппарата:
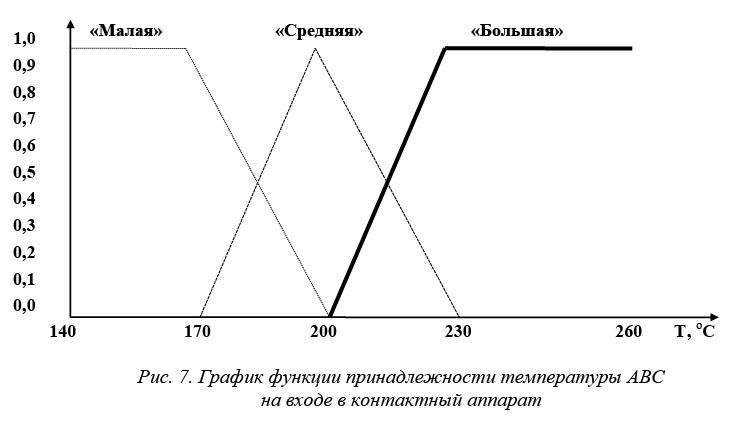
– температура аммиачно-воздушной смеси на входе в контактный аппарат («малая», «средняя», «большая»);
– давление аммиачно-воздушной смеси на входе в контактный аппарат («малое», «среднее», «большое»);
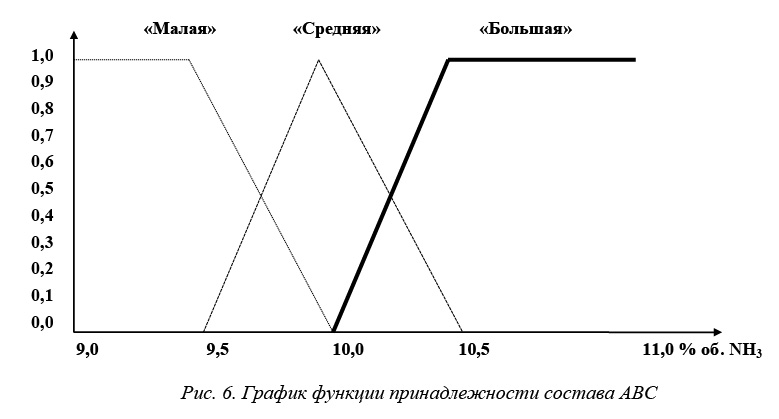
– состав аммиачно-воздушной смеси на входе в контактный аппарат («малая», «средняя», «большая»);
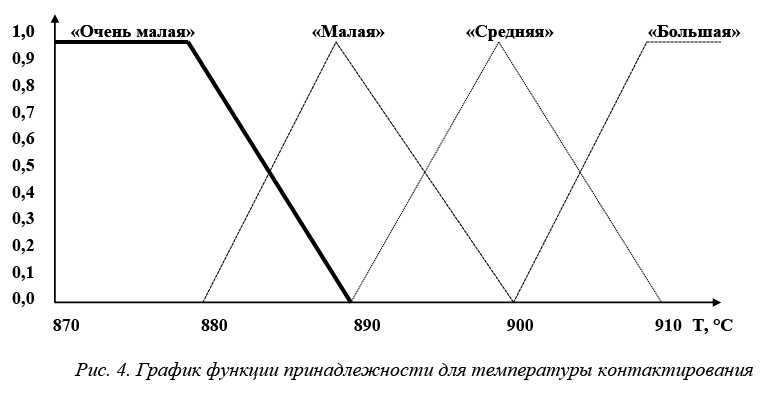
– температура контактирования («очень малая», «малая», «средняя», «большая»).
В соответствии с базовой шкалой для каждого признака выбраны названия термов. Как уже говорилось, значения лингвистических переменных из терм-множеств описываются нечеткими переменными. Графики функций принадлежности этих нечетких множеств приведены на рисунках 4–7.
Каждый признак описывается соответствующей лингвистической переменной <yi, Ti, Di>,
где уi – название лингвистической переменной, Тi – множество лингвистических значений переменной, Di – область ее определения (базовое множество).
Например, пусть оценивается температура аммиачно-воздушной смеси на входе в контактный аппарат с помощью понятий «малая», «средняя», «высокая».
Температура изменяется от 170 до 230 оС. Формализация такого описания может быть проведена при помощи лингвистической переменной <«Температура АВС», Т, [170, 230]>, где Т={«малая», «средняя», «большая»}. Значения лингвистической переменной «Температура АВС» из терм-множества Т описываются нечеткими переменными с соответствующими наименованиями и ограничениями на возможные значения. Например, значение «малая» задается нечеткой переменной <«малая», [170, 200], С>, где нечеткое множество может быть следующим: С={<1/170>, <0,8/175>, <0,5/185>, <0,1/198>}.
Общее число элементов алфавита или эталонных ситуаций равно произведению чисел термов по каждому из вышеназванных параметров: 3*3*3*4=108.
Рассмотрим порядок выбора значений параметров, соответствующих определенным значениям элементов алфавита.
Для описания температуры контактирования используются четыре терма: < «очень малая»
[870–890 oC], Тэточень малая = 880 oC; «малая» [880–900 оC], Тэтмалая =890 oC; «средняя» [890–910 oC],
Тэтсредняя =900 oC; «большая» [900 oC и выше], Тэтбольшая =910 oC>.
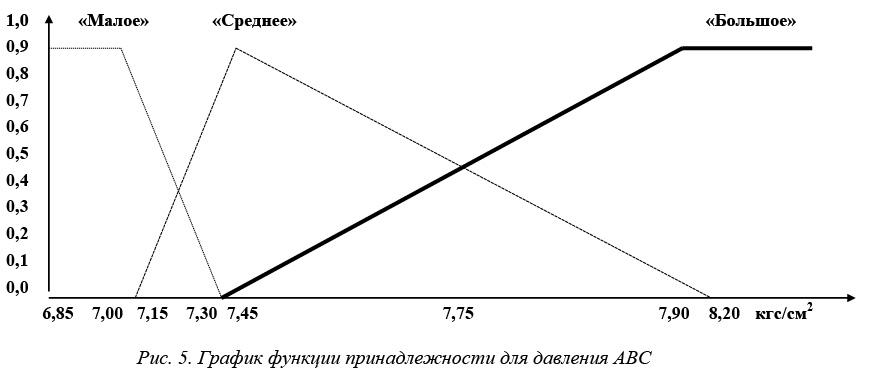
Параметр «Давление АВС», три терма: <«малое» [6,85–7,15 кг/см2], Рэтмалое= 7,00 кг/см2; «среднее» [7,00–8,05 кг/см2], Рэтсреднее= 7,15 кг/см2; «большое» [7,15 кг/см2 и выше], Рэтбольшое= 8,05 кг/см2>.
Состав АВС, три терма: <«малое» [9,0–10,0 % объема NH3], Кэтмалое= =9,5 % объема NH3; «среднее» [9,5–10,5 % объема NH3], Кэтсреднее=10,0 % объема NH3; «большое» [10,0 и выше % объема NH3],
Кэтбольшое= 10,5 % объема NH3>.
Температура АВС, три терма: <«малая» [140–200 oC], Тэтмалая = =170 Co; «средняя» [170–230 oC],
Тэтсредняя =200 oC; «большая» [200 oC и выше], Тэтбольшая =230 oC>.
Каждый терм соответствует определенному интервалу значений заданных параметров. Эталонное значение параметра для каждого терма назначалось по максимальному значению функции принадлежности, соответствующей данному терму.
Проверка показывает, что эталонные ситуации не содержат нечетко равных между собой ситуаций.
Рассмотрим пример принятия решений советующей экспертной системы.
Предположим, что произошло повышение температуры аммиачно-воздушной смеси на входе в контактный аппарат и наравне с этим понизилась температура контактирования. Оператор, видя отклонения в работе агрегата, подозревает о возникновении критической ситуации и обращается к системе за консультацией. В систему вводятся параметры, вызвавшие отклонения в работе контактного аппарата.
Очевидно, что данная ситуация является нечеткой, размытой, так как на основании отклонения многих параметров можно принять несколько решений об управлении. Используя графики принадлежности термов нечетких параметров (рис. 4–7), нечеткую ситуацию представим в виде
{<<0,0/«очень малая», 0,9/«малая», 0,1/«средняя», 0,0/«большая» >/ «Температура контактирования»>, <<0,19/«малое», 0,81/«среднее», 0,0/ «большое»>/«Давление АВС»>, <<0,0/«малый», 0,82/«средний», 0,18/ «большой»>/«Состав АВС»>, <<0,0/«малая», 0,1/«средняя», 0,9/ «большая»>/«Температура АВС»>}.
Далее рассчитываются степени включения входной ситуации в эталонные и степени включения эталонных ситуаций во входную ситуацию для того, чтобы найти степени нечеткого равенства входной ситуации с какой-либо из эталонных ситуаций.
На основании полученных результатов по «решающей таблице» определяются возможные альтернативные управляющие решения, соответствующие наиболее близким эталонным ситуациям, которые выдаются в виде рекомендаций пользователю.
Литература
Матвеев Н.М. Дифференциальные уравнения. Минск: Высшая школа, 1968. 545 с.
Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.: Наука, 1974. 332 с.
Петровский И.Г. Лекции об уравнениях с частными производными. М., Ленинград: Государственное изд-во технико-теоретической литературы, 1950. 351 с.
Мизохата С. Теория уравнений с частными производными. М.: Мир, 1977. 504 с.
Чирков М.К. Основы общей теории конечных автоматов. Л.: Изд-во ЛГУ, 1975. 282 с.
Глушков В.М. Синтез цифровых автоматов. М.: Наука. Гл. ред. Физматлит, 1962. 476 с.
Бауэр В. Введение в теорию конечных автоматов. М.: Радио и связь, 1987. 382 с.
Богатиков В.Н., Палюх Б.В. Построение дискретных моделей химико-технологических систем. Теория и практика. Апатиты: Изд-во Кольского научного центра, 1995. 164 с.
Производство азотной кислоты в агрегатах большой единичной мощности; [под ред. В.М. Олевского]. М.: Химия, 1985. 400 с.
MATHEMATICAL MODELS OF THE PROCESSES OF CHEMICAL TECHNOLOGY.
CHARACTERISTICS OF THE MATHEMATICAL PROPERTIES OF TECHNICAL OPERATORS
Vent D.P., Dr. Sc. (Engineering), Professor; Prorokov A.E., Ph.D. (Engineering), Associate Professor;
Sanaeva G.N., Senior Lecturer
(Novomoskovsk Institute of MUCTR. D.I. Mendeleev, Druzhby st. 8, Tula Reg., Novomoskovsk, 301665,
Russian Federation, k_vtit@dialog.nirhtu.ru);
Toichkin N.A., Ph.D. (Engineering), Associate Professor, toichkin@list.ru
(Kola branch of Petrozavodsk state University, Lesnaya st. 29, Murmansk Reg., Apatity, 184209,
Russian Federation);
Palyukh B.V., Dr.Sc. (Engineering), Professor; Semenov N.A., Dr.Sc. (Engineering), Professor;
Bogatikov V.N., Dr.Sc. (Engineering), Professor; Alekseev V.V., Ph.D. (Engineering), Associate Professor; Kemaykin V.K., Ph.D. (Engineering), Associate Professor
(Tver State Technical University, Nikitin Quay 22, Tver, 170026, Russian Federation, is@tstu.tver.ru)
Abstract. The paper focuses on the construction of various mathematical models of chemical technology processes. An approach to the construction of chemical-technological system discrete models for typical processes of chemical technology, described by systems of ordinary differential equations and partial differential equations, which correspond to typical models of chemical technology processes (ideal mixing model, ideal displacement model, diffuse model).
The methodology for constructing discrete models (method of states separation, models based on differential equations in partial derivatives, model based on fuzzy sets) of continuous chemical-technological system, which can be applied for diagnostic states of technological process and and control of their safe functioning.
Construction of discrete models of continuous chemical-technological system, lets be attributed the instantaneous state of the technological process to a class of states. The main purpose of this stage – modeling of event processes occurring in the object control and reflection of causal relationships existing in technological process, equipments and control systems.
Keywords: technological safety, chemical-technological process, mathematical model, security control, object control, discrete models, state of the process, chemical-technological system.
Comments