(Работа выполнена при финансовой поддержке гранта РФФИ № 17-07–00997)
Одним из перспективных вопросов при решении конструкторских задач, а именно задачи размещения элементов сверхбольших интегральных схем (СБИС), является попадание алгоритма в локальную яму (оптимум).
Учитывая вышесказанное, актуальной является разработка различных продуктивных методов, архитектур и алгоритмов поиска перспективных решений. В целях повышения эффективности решения задач конструкторского проектирования будут применены методы эволюционного моделирования, генетического поиска, а также принципы самоорганизации и адаптации.
В настоящее время активное развитие получили методы, основанные на моделировании поведения живой природы. Интегрируя поведенческую модель живой природы на определенные сферы человеческой деятельности, мы имеем возможность получить эффективный инструмент решения поставленных задач [1–3]. В работе поведенческая модель живой природы будет отображена в роевом алгоритме поиска решений. Системы роевого интеллекта являются многоагентными системами, то есть состоят из множества агентов, которые локально взаимодействуют между собой и с окружающей средой. Каждый агент очень прост, но, применяя коллективный разум, агентами создается так называемый роевой интеллект.
В качестве роевого интеллекта будет применен пчелиный алгоритм.
Постановка задачи
Представим решение в виде множества элементов, а исходные данные в виде графовой модели. Граф G(X, U), где Х – множество вершин (|Х|=n), U – множество ребер [4]. Дано: граф, множество позиций. Целевая функция F = , где dj – длина Uj. Решение представляется в виде вектора R={ri | i=1, 2, …, n}, где ri – номер вершины, помещенной в позицию Pi. Необходимо F→ min.
Разработка роевого алгоритма размещения
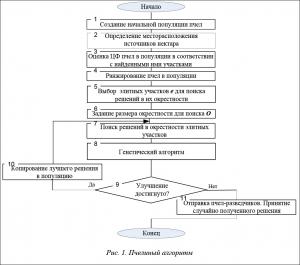
Опишем пчелиный алгоритм размещения элементов сверхбольших интегральных схем (рис. 1).
На первом этапе вводим параметры схемы и алгоритма, параметры поля с количеством посадочных мест по горизонтали и вертикали. Далее вводятся параметры роевого алгоритма, такие как количество агентов, максимальное количество итераций алгоритма, минимальное и максимальное количество агентов-разведчиков. На следующей итерации формируются случайные решения. На первом шаге роевого алгоритма все агенты (пчелы) находятся в улье. Далее пчелы-исследователи отправляются для исследования окрестностей. Начальная позиция для каждой пчелы задается случайным образом [5–8].
На найденных позициях происходит оценка целевой функции (ЦФ). Для каждой пчелы определяется лучший (элитный) участок, который она посещала с начала первой итерации, и значение ЦФ fiti на этом участке. Участки е, на которых значения ЦФ больше (элитные участки), отбираются для поиска решений в их окрестностях. Далее происходит отбор пчел с лучшими значениями ЦФ. Формируется популяция, основанная на элитных участках (с большим показателем ЦФ). После проведенного поиска лучшего решения ЦФ сформируем матицу решений ЦФ и возвращаемся на новую итерацию поиска решений. Количество поиска решений полностью зависит от количества итераций. После нахождения лучшего решения ЦФ результат фиксируется в матрицу связности. Полученное решение выводится графически в виде размещения компонентов (деталей в посадочных местах). Уже размещенные элементы перераспределяются и устанавливаются в новые посадочные места, предварительно размещенные на коммутационном поле.
Метод поиска окрестностей в роевом алгоритме
Основную роль в поведении роя пчел играет самоорганизация. Достижение общих целей пчел обеспечивается за счет низкоуровневых взаимодействий.
Одним из важных механизмов в работе пчелиного алгоритма является исследование перспективных позиций в окрестности поиска решений. В работе предлагается метод формирования окрестности позиций в пространстве решений [9–11].
Рассмотрим метод исследования перспективных позиций в окрестности поиска решений на основе работы пчелиного алгоритма (рис. 2). Вначале формируется область поиска решений и пчелы-разведчики находят основные базовые окрестности. Далее пчелы-фуражиры исследуют найденные решения. Для данных (найденных) решений оценивается ЦФ. Из каждой окрестности выбираются лучшие решения,
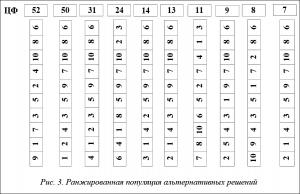
то есть те решения, где ЦФ больше, и создается начальная популяция для дальнейшей работы генетического алгоритма. Вводится управляющий параметр α. Для найденных решений используем управляющий параметр α = 1…100. Использование управляющего параметра дает возможность как сужать пространство поиска решений, так и расширять его (рис. 2) [6, 7, 12–14]. На рисунке 3 предложен способ ранжирования популяций альтернативных решений.
Экспериментальные исследования
Проведены экспериментальные исследования, позволяющие оценивать качество решения разработанным алгоритмом, а также скорость решения поставленной задачи и выявлять зависимость времени работы от количества элементов схемы. Эксперименты проводились на итерационном, эволюционном
и роевом алгоритмах.
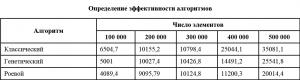
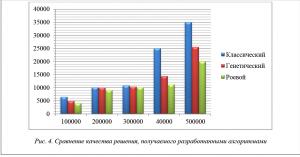
В целях определения перспективности разработанного алгоритма проведены исследования на тестовых примерах. Под перспективностью понимается качество размещения. Основные результаты эксперимента приведены в таблице и на рисунке 4.
Из гистограммы (рис. 4) видно, что при размещении более 100 000 элементов перспективным является разработанный роевой алгоритм.
Заключение
В работе рассмотрен метод исследования окрестностей в природных алгоритмах для решения конструкторских задач. Представлена постановка задачи. Описан процесс поиска решений на основе пчелиного алгоритма. Рассмотрен роевой алгоритм решения конструкторской задачи на основе адаптивного поведения пчелиной колонии. Описана важная задача конструкторского проектирования – размещение элементов СБИС.
Одним из важных механизмов в работе пчелиного алгоритма является исследование перспективных позиций в окрестности поиска решений. В работе предлагается метод формирования окрестности позиций в пространстве решений.
Авторами предложен новый принцип поиска перспективных позиций на основе работы пчелиного алгоритма. Введен управляющий параметр α для возможности как сужать пространство поиска решений, так и расширять его.
Проведенные исследования позволяют судить о том, что вычислительная сложность алгоритма не выходит за пределы полиномиальной зависимости. Разработанный алгоритм дает возможность находить квазиоптимальные решения за полиномиальное время.
Литература
- Лебедев О.Б. Модели адаптивного поведения муравьиной колонии в задачах проектирования: монография. Таганрог: Изд-во ТТИ ЮФУ, 2013. 199 с.
- Лебедев В.Б., Лебедев О.Б. Роевой интеллект на основе интеграции моделей адаптивного поведения муравьиной и пчелиной колонии. Изв. ЮФУ: Технич. науки; Тематич. вып.: Интеллектуальные САПР. 2013. № 7. С. 41–47.
- Кулиев Э.В., Лежебоков А.А. Исследование характеристик гибридного алгоритма размещения // Изв. ЮФУ. 2013. № 3. С. 255–261.
- Lezhebokov A., Shkalenko B., Kuliev E. A new approach for software development in terms of problem-oriented knowledge search and processing. Advances in Intelligent Systems and Computing. 2016, vol. 450, pp. 297–306.
- Страхов Н.Э., Кулиева Н.В., Семушина Н.С. Модифицированный алгоритм решения задачи размещения компонентов СБИС // Программная инженерия: методы и технологии разработки информационно-вычислительных систем (ПИИВС-2016): сб. науч. тр. I науч.-практич. конф. Донецк: Изд-во Донец. национальн. технич. ун-та, 2016. С. 201–203.
- Новиков А.А., Кулиев Э.В., Самойлов А.Н. Когнитивная архитектура агентов мультиагентной системы // Информатизация и связь. 2016. № 2. С. 127–131.
- Kureichik V.V., Zaporozhets D.Y., Zaruba D.V. Partitioning of vlsi fragments based on the model of glowworm's behavior. Proc. 19th Intern. Conf. SCM-2016. 2016, pp. 268–272.
- Холопова Н.В., Дьяченко М.А. Биоинспирированный подход решения задачи размещения // I Всероссийская научно-техническая конференция молодых ученых, аспирантов и студентов: сб. ст. Ростов н/Д: Изд-во ЮФУ, 2015. С. 420–423.
- Холопова Н.В., Самойлов А.Н., Кулиев Э.В. Бионический поиск решения конструкторских задач // Изв. ЮФУ: Технич. науки. 2015. № 7. С. 53–62.
- Курейчик В.М., Лебедев Б.К., Лебедев О.Б. Адаптация в задачах проектирования топологии // Проблемы разработки перспективных микро- и наноэлектронных систем: сб. науч. тр.; [под ред. А.Л. Стемпковского]. М.: Изд-во ИППМ РАН, 2010. С. 170–177.
- Кулиева Н.В., Логинов О.А., Лебедева Е.О. Комбинированный алгоритм решения задачи размещения // Конгресс по интеллектуальным системам и информационным технологиям «IS&IT16»: сб. тр. Ростов н/Д: Изд-во ЮФУ, 2016. С. 82–86.
- Кулиев Э.В., Лежебоков А.А., Кравченко Ю.А Роевой алгоритм поисковой оптимизации на основе моделирования поведения летучих мышей // Изв. ЮФУ: Технич. науки. 2016. № 7. С. 53–62.
- Лебедев Б.К., Кулиев Э.В., Холопова Н.В. Генетический алгоритм разбиения с учетом принципов биогеографии // Информатика, вычислительная техника и инженерное образование. 2015. № 3. С. 1–9.
- Терещенко Д.Ю., Кравцова А.А., Кулиева Н.В. Об одном методе решения задачи размещения элементов СБИС // Информационные технологии, системный анализ и управление (ИТСАУ-2016): сб. тр. ХIV Всерос. науч. конф. Таганрог: Изд-во ЮФУ, 2016. С. 228–232.
- Курейчик В.В., Полупанова Е.Е. Эволюционная оптимизация на основе алгоритма колонии пчел // Изв. ЮФУ: Технич. науки. 2009. № 12. С. 41–46.
- Курейчик В.М., Лебедев Б.К., Лебедев О.Б. Решение задачи размещения на основе эволюционного моделирования // Изв. Акад. наук: Теория и системы управления. 2007. № 4. С. 78–90.

Comments