The developing actuality of the optimal method complex and the problem-solving algorithms of the image processing for the optoelectronic device (OED) is due to the aprior force principium in the space domain of the specifics and the observed image mathematical descriptions. This is the calibration signal way which has an additive overlapping the OED background and internal noises on it. This method is the base of the detecting device objects [1–4] framework on the phono-target frame (PTF) images.

There is a weighty conclusion from the relevant mathematical models of the OED forming image: it takes the evidential organization of the function types. This aprior describes the optical radiation of the dynamic object (DO) which has their definition and meaning specialized areas. The accounting effects of the distribution environment impact are very important. This is necessary for the offered watch equations realization in the object detection algorithms.

However, the function generation is unsolved problem in practice. The impossibility both a priori problem and the DO indicatrix of dissipation reconstruction in current conditions and also in different going of typical DO, the side illumination, the atmosphere state are indeterminacy [5].

That is why the watch equation must have the development under uncertainty in relation to possible, in general case – ambulatory, present states of viewing conditions and the optical radiation of objects, subject to detection, tracking, and identification.

Taking into account the noted above – new optimal method became the theoretical foundation to create the regarded software application. The computer equipment realizes the algorithms for detection, tracking, and identification of DO types in different light and flying environment [6–8]. Setting and solving the unified complex of problems help their development. The unified complex of problems corresponds to the problems which also occur when there is a modern OED development.

Next there are the ways and solving results for the marked problems.

Images on the OED PTF are the bivariate probability discrete process realization. This realization is in conditions of DO presence or absence in the control space zone.

The watch equation describes this process [8, 9]. Take no account of the conditions it has background
and additive elements – uncorrelated gaussian noise correctly is OED:

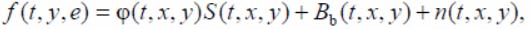
where f(t, x, y) – matrix function of brightness variation (intensity) in the image point (x, y) of the phono-target scene on the OED output; φ(t, x, y) – matrix function of variation propagation medium of radiation; S (t, x, y) – matrix function of the DO brightness variation in the image plane; B_b(t, x, y) – matrix function of background brightness; n(t, x, y) – matrix function of the basic additive noise on the OED output.

The smoothing operation activity for every image significantly lets down the gaussian noise effect. The image smoothing by the regularizable variational method is the solution of the difference equation of the form:

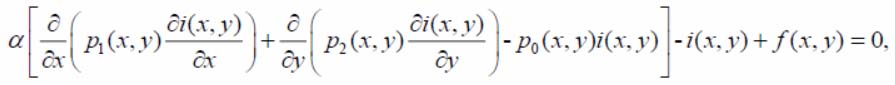(1)

with boundary data:

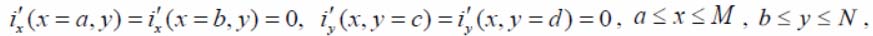
where a – regularity factor; f(x, y) – measured function – the image on the PTF; p₀(x, y), p₁(x, y), p₂( x, y) – weight functions, elective with account for additional a priori data about the function type f(x, y) and its observational error; i(x, y) – smoothed function – the image on the PTF.

The author made the image property analyze with the wavelet-correlation method and fractal geometry
[8, 10]. The wavelet is on the basis of the wave extended spheroidal function (WESF) of zeroth order.

The coefficient determination is in accordance with the operating sequence in [8, 11].

The counted wavelet coefficients have a check test to the ownership of the DO presence in the OED control zone (hypothesis H₁) or an alternative situation (situation H₂) – DO absence (in the OED control zone is only complex background).

The author uses the Neumann-Pearson criterion for the decision about the affiliation with the image wavelet coefficients to the cluster with the DO [11, 12].As the result there are image pixel clusters which have the information about the presence evidence of the valid DO in the OED control zone, and the image pixel clusters which have only background information. The clusters are adaptive in reference to the image constitutive properties on every current PTF. It means that they are adaptive to the brightness jump and to the change of their smoothness upon fractal geometry criterion. It is very important in case of the DO negative contrast.

The image segmentation has an automat effect by selected clusters. It happens with the optimal rectangular windows. They cover the clusters and their attitude position on the OED PTF. The DO on the images or the goal- like images must be there. The desired rectangular windows have the ability to rebuild as the fixation result of left y _li and right y_ri bounding columns of every cluster wavelet- coefficients and its top – x _tj and low – x_lj bounding line of the wavelet-coefficients i, j = 1, …, L. The windows have a record (in PTF coordinates) as y ≥ y _li, y ≤ y_pi, x ≥ x _tj, x ≤ x_lj.

The author uses minimal sufficient statistics as the DO detection statistics: fractal (partitive) dimension and the maximum eigenvalue of the correlative matrix of every PTF windows pixel brightness [13, 14]. The statistics are invariable in reference to the DO image contrast and its flying singularity.

The window image fractal dimension is a random size. It accepts a value from the terminal positive interval and complies with the unimodal beta-distribution (exponential law). This dimension is invariable in reference to the image contrast symbol and DO turning during the movement. The image fractal dimension in windows has the estimating by the cover method. Its foundation is the realization of fractal dimension fundamental definition.

The matrix correlation maximum eigenvalue of the PTF window image pixel brightness as a minimal sufficient statistic has fundamental property. It is a maximum invariant and its use objectively leads to the DO detector building upon Neumann-Pearson criterion. To date, such statistics didn’t have usage in the OED image operation.

The famous literature analysis [9, 12, 14, 15] shows, that authors built the detectors, which have a plan only on particular conditions of OED image getting with a positive contrast of image objects and they essential depend on the reliability of the a priori data used in them.

There are no methods and recommendations for solving emerging problems in these.

The maximum eigenvalue calculation of auto – and cross-correlation matrixes are in accordance with QR- algorithm, where Q – orthographic, and R – upper triangular of matrix. In applying for the DO statistic detection as maximal invariants by way of maximum eigenvalue of image pixels correlation matrix and its fractal dimension we don’t need a priori data entry which are in announce papers. The DO detector becomes optimal according to Neumann-Pearson principium. And its structure is universal as in reference to low (point)-sized and space extendedDO images, as to the DO image contrast sign and the DO flying features. The validity of the statement follows from the positive definiteness parameter of correlation matrix and algorithm independence for calculation of this matrix and fractal dimension algorithm for calculation from the DO image contrast sign and the DO flying slewing.

The DO detection on the image f(t, x, y) boils down to the coordinates setting of the window level, where the window selective field f(t, x, y) has a fractal dimension, corresponding with the required accuracy to the radiated field from the DO and accompanying interference from external sources, and also to the allocation of limiting object point on the window image.

The likelihood function while analyzing series from N-images, formed by OED on the such timespan [t₁, t_N], that the series, due to the property without inertia of OED, introduces a duplicated sample of independent images. It has a form [8]:

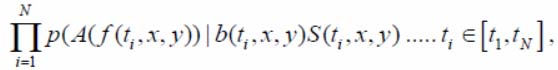
where A – transformation operator to the scalar maximum own value of correlation matrix for an analyzable image f( t_i, x, y) in window on the PTF, entered in i -moment (i-frame);

b ₁ , b₀₁, b₀₂ – a disparate source name of the background light, taking effect on the OED;

The component b(t_i, x, y)S( t_i, x, y) – reference image which is a watch equation summary.

The timespan [t₁, t_N] can «slide» along the time base and the series composition will change. That is why there is a recurrence scheme in the compiled likelihood function calculating.

An assure of necessary truthfulness for the setting window location, covering the image from the DO with the accompanying radiation brightness level from the background source, is in getting the DO β-pass bare possibility by non-exceedance accepted level of false alarm – a_d probability.

The optimum criterion structure of taking a decision forms in according to the Neumann-Pearson principium in a way .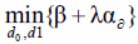

There will be d₁ (there is a DO on the separately analyzed PTF), if the inequality is:

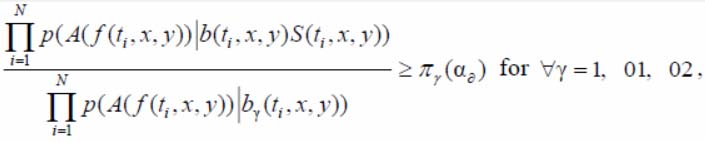                              (2)

otherwise there is an alternate hypothesis d₀.

During the development there is a new method of the DO detection by small- size «point» images which are proximal to the target-like background formations [8]. The DO image configuration will be conditioned by the OED – DO distance and a state of the atmosphere and background. There is a research and detection. The DO image configuration will be conditioned by the indicatrix special aspects of the object integral brightness. The image can be point and extended.

The evidential detection of the point DO in the difficult environment is possible only with locally most powerful tests and taking a decision about the DO detection to put into practice as the deposit accumulation result N-consecutive PTF. The difficult environment has the functions proximity of the situation plausibility – the OED operating conditions: H_k=1 – «in the OED overview zone is only difficult background» or H_k=2 – «in the OED overview zone is a OD on a difficult background» The PTF primary sequence forms on every fixed short sliding time period – a slide strobe and represents the second sample.

The DO detection criterion has synthesis on the low-contrast image with using of dependence of approximate likelihood function H_k=1 and H_k=2 of vectorized retrieval with statistically independent components: d_{ν i} – fractal dimension and λ_maxνi – maximum eigenvalue of space correlation matrix of image brightness in v-window of i-frame:

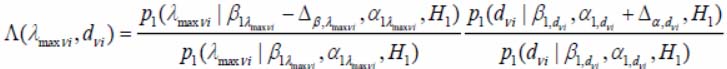
The situation proximity is a distance between the likelihood beta-functions of sampling action as the way of the low-contrast image «point» upon condition for one and the other alternative situations.

The following operations results determine whether the binary storage device detects a dynamic object
on the OED image:

- the statistics calculation for the decision-making criterion for detecting the DO presence sign in the OED review zone ln(1-d_νi), ln(1-λ_{max νi} );

- the verification of the Neumann-Pearson criterion for detecting the DO presence sign in the OEP review zone based on the calculated statistics y = ln(1 – dνi), y = ln(1 – λmaxνi) and the binary quantized signals formation (from ones and zeros). Thresholds for making a decision about theDO detection Th(α_ad; λ_maxν, Th(α_ad; d _νi) have expressions [8]:

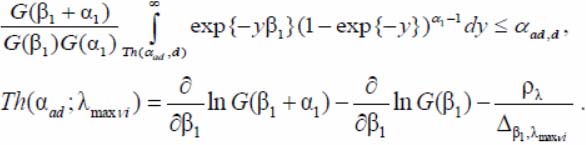
Developed the DO wavelet-fractal and correlation recognition algorithm [8] has an adaptive hierarchical stable structure that is the invariance to various features of the target environment (TE) and the DO trajectories proximity, and also to various "spikes" and variations in samples of coordinate measuring of the DO detected attitude position. The algorithm is highly sensitive to the of the DO motion parameters of different types. There are two vectors criteria for the implementation of the DO type: the non-local vector criterion for recognizing non-close DO types and the local criterion for recognizing close DO types. The DO classification according to «close-not close» is the condition:m_i – m_j ≫ d₁, s_i – s_j ≫ d₂,m_i > m_j, s_i > s_j, for not close DO type and m_i–m_j ≫ δ₁, σ_i – σ_j ≫ δ₂ for close type, where i, j – DO type index, m, s – the likelihood function parameters, δ₁, δ₂ – small values have a formula d = 2/√n, n – sample size [8].

In the case of the non-close types DO identification, the criterion components for obtaining at each current interval [t – T, t] independent implementations of sufficient statistics d(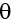), d(φ), d(D_max), i(w(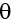)), i(w(j)), i(w(D_max)), l(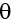), l(j), l(D_max) are in [8], where D_max – maximum distance; 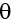– position angle; j – azimuth; d(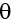), d(j), d(D _max) – fractal dimensions access of distance measurement, position angle, and azimuth accordingly; i(w (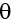)), i (w(j)), i(w(D_max)) – the wavelet spectra energy 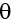, j, D _max; l(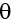), l(φ), l(D_max) – the correlation matrix maximum eigenvalue 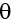, φ, D_max.

The D_max distance has the expression which is in [15]. The solution γ_{j = 1} for each component (inequality) has an application if the corresponding inequality has an execution for (j = 1, i = 2) Ù (j = 1, i = 3); the solution γ_{j = 2} has an application when performing inequalities for (j = 2, i = 1) (j = 2, i = 3) and the solution γ_{j = 3} has an application when performing inequalities for ( j = 3, i = 1) (j = 3, i = 2).

The left part defines the identification criteria for statistics, and the right part of the expression defines
the criteria threshold value (for d(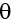)) [12, 15].

The criterion is as the detector binary vector and in the performance of any nine inequalities and the corresponding critical function 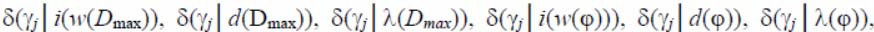 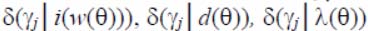 takes the value 1 otherwise 0.

As a result, there will be a set of ones and zeros for each DO detection current. In this case, the actual decision on the DO type in accordance with the" majority rule " the authors should take according to statistics L = ∑ζ_ν according to the criterion L > C, С – the threshold level (unit number), ν = 1, ..., 9 – the inequality index of the type from (1), ζ_ν = 1 or ζ _ν = 0 when the inequality has fulfillment or not.

The threshold value is C ≈ 1.5√M, M = 9- the vector dimension of the solving functions (below in the algorithm C = 6 as a guaranteed value).

If the criterion L > C = 6 is not fulfilled, but the criterion L ≥ C = 5 is fulfilled, there will be a transition to checking (using the same samples of sufficient statistics) the criteria for recognizing close hypotheses – the DO type.

The value of C= 5 agrees with the optimal value of C ≈ 1.5√ M for M= 9 – the algorithm number that implements the nine-dimensional vector criterion (1), and there is the fact for the vector case that the result stability (in this case, the non-fulfillment of the condition L ≥ C = 6 result) must always have a test for fractional deviations.

For DO close types to the recognition criteria

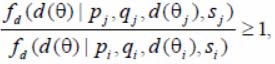
when p_j = p_i + δ _p has an expression, from [12, 15], where there is a criterion decision rule.

Criteria are the most powerful unbiased ones. The decision about the detected DO type by the algorithm is automatic, based on a binary serial procedure with two threshold levels for the criterion «at least once 3 out of 5». On one threshold there is a decision about the detected DO type, on the other there is a decision to connect algorithms that implement criteria for recognizing the similar DO types. The criteria are Bayesian, constructed with a simple loss function and a priori proportional as the least favorable distribution on the set of all the DO possible types [12, 15].

A coordinate evaluating method of the DO space position when it is accompanied by the PTF sequence is as a non- linear interpolation filter estimation the DO coordinates, adaptive to the DO maneuver with feedback [8].

The methods and algorithms described above are in the form of information-related computing modules that are part of a software package that implements a complex algorithm for processing 2D images for the OES data detection, tracking and identification.

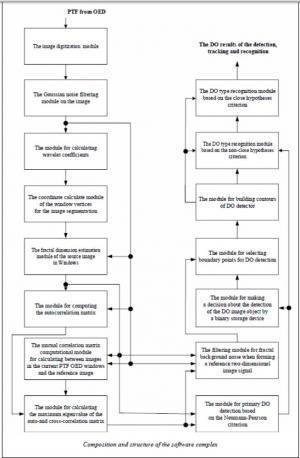
The software package is in the MATLAB application package. It forms the basis for synthesizing complex programs for studying the performance characteristics of both private DO detection and tracking algorithms, and a complex algorithm for evaluating the current state of the PTF's controlled OED [8]. Software packages work in real time on modern computers (see figure).

The Gaussian noise filtering module on the image takes out or significantly reduces the effect of additive Gaussian noise by each image smoothing operation, implemented by the numerical solution of equation (1).

The wavelet coefficients computing module calculates the WESF coefficients. The window vertex coordinates calculating module for image segmentation performs the optimal image segmentation with automatic DO detection on each current OED PTF.

Segmentation is by means of the Neumann–Pearson threshold cluster selection containing the DO images in the OED control zone and/or target-like images, with using one-dimensional wavelet transformations of rows and columns of the PTF.

The cluster selection contains the DO information. It is as a result of checking already calculated the corresponding wavelet coefficients on the affiliation situation of the DO finding in the OED control zone (hypothesis H1) or an alternative situation (hypothesis H2): The DO absence says that in the OED control zone is only complex background.

There is a Neumann–Pearson criterion for deciding whether each image wavelet coefficient belongs to the DO cluster. It has the expression definition given in [8].

The selected clusters are the PTF image segmentation result. They have a single-valued transformation in the 2D pixel coordinate space of the original PTF with the values of their brightness of the received optical radiation OEP. There are the pixel clusters with the optical radiation brightness either from the DO or from the background on the PTF. The rectangular windows cover such clusters with minimal areas; fractal characteristics can also have calculation directly from the selected cluster structures.

The fractal dimension estimating module of an image in windows allows getting the fractal dimension value with using the coating method.

The autocorrelation matrix calculation module performs calculations in accordance with the algorithm from [8].

The module for calculating the cross-correlation matrix is between the current PTF OED windows images and the reference image. A reference image is the DO image, formed according to the PTF, immediately preceding to the current one and representing a scale copy in relation to the true (undistorted by interference) DO image on the current frame. The integrating result of the product copy onto the DO image for the current frame uniquely corresponds to the maximum output effect of the matched two-dimensional filter [8].

The reference image has a processing from window images that cover selected wavelet clusters of pixel brightness on each analyzed current PTF. The important condition is that such images have a fractal dimension value characteristic that exceeds the value of the background fractal dimension estimated for the current frame.

When forming a reference image, there are the following operations:

- calculating with using a direct two-fold Fourier transform of the spatial frequency spectrum (SFS) in the selected windows of the current image with a fractal dimension that exceeds the background fractal dimension;

- the SFS calculation in windows containing only the background image;

- the SFS background and the OED internal noise from the calculated SFS;

- the representation of the getting as a result of the subtraction operation by the form expression:

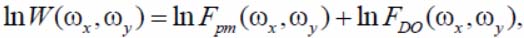
where w_x, w_y – discrete space frequencies of the window images in the PTF coordinate system;F_DO(ω_x, ω _y) – two-dimensional spectrum of the DO optical radiation; F_pm(w_x , w_y) – two-dimensional spectrum of optical radiation of the propagation medium multiplicatively affecting the DO radiation in the space sector "covered" by the wavelet window, where the DO can be; W(ω_x, ω _y) – the window spectrum of the analyzed image;

- the SFS image calculation:

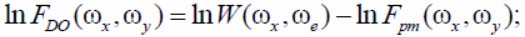
- performing the inverse Fourier transform spectrum F_DO (w_x, w_y).

The reference image synthesized in this way is for use in the cross-correlation matrix formation, which is an information basis for solving the problem of the DO detection on the next OED PTF current image.

The module for calculating the maximum eigenvalue of the auto- and cross-correlation matrix implements calculations in accordance with the QR algorithm [8].

The Neumann–Pearson primary DO detection module realizes an algorithm for detecting a spatially extended object in accordance with the formula (2).

The fractal background noise filtering module is when forming a two-dimensional reference signal-an image.

Background filtering on the current PTF is in the space-frequency domain, that is, based on the space-energy spectrums (SES) of the observation equation left part and the component terms in the right part of the equation, provided that for the term B_b( i, x, y). The SES can have an estimate for clusters of the current image that do not contain information about the DO. Fractal dimension indicators reliably distinguish such clusters.

The SES f(i, x, y) and B_b( i, x, y) calculated two-dimensional discrete «window» Fourier processing, and the SES term j(i, x, y) S( i, x, y) is as the difference between SES window functions f(i, x, y) and B_b(i, x, y). As a result, there are the source data for forming a reference image in the form of either j(i, x, y) S(i, x, y), or S(i, x, y). The first of these cases takes place under conditions of complete a priori uncertainty about the atmosphere current state – the transmission medium of the DO optical radiation. The second is when it is possible to get the information about the transmission of optical radiation by the atmosphere in the OED control zone. The accepted filtering principle, taking into account the non-stationary TE, is adaptive to the image changes on the PTF.

The decision module for detecting the DO binary storage implements the algorithms for detecting the point low-contrast DO. To select the boundary points of the detected DO, the authors use the integral image differentiation operator in the window. This operator, when calculating the input signal derivatives (a two-dimensional image in a window), simultaneously implements the requirement to suppress high -frequency noise components on each frame [8]:

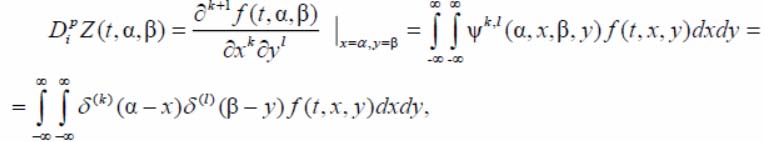
where p – derivative order; 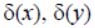 – delta-functions,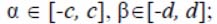

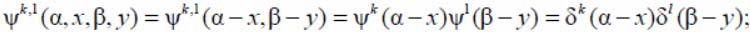
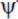– weight function, the type of separable space-invariant weight functions.

In this case, the boundary points detection of differences in images is by sequential processing of sample data f(t, x, y) in the window with DO.

The selected boundary points restore the contour of the detectedDO. The contour is set parametrically as two functions: x = x(i), y = y(i), where i is a parameter. When approximating a contour with Hermitian cubic splines S(x, i) and S( y, i), its geometric characteristics have calculations in accordance with [8].

The contour approximation contour by Hermite parametric cubic splines is according to [4]. Hermitian splines have an advantage over other types of splines – they do not require solving systems of linear algebraic equations to determine their coefficients.

Recognition modules based on the criteria of close and non-close hypotheses implement object recognition in accordance with [8, 16].

Conclusion

The proposed methods and algorithms are advance of the achieved level in well-known works, determine the scientific significance of the work performed and the authors published it in leading peer-reviewed Russian scientific journals and publications. A detailed description of the developed methods and algorithms is in [8]. The proposed software package implements the procedures for detecting, tracking and identification of dynamic objects in the absence of a priori data on the TE current characteristics in the OED control zone for point and extended low-contrast targets with positive and negative contrasts.

Acknowledgements: The paper is part of the state task of the Ministry of education and science of the Russian Federation, code 2.1777.2017 / ПЧ.

Referenses

1. Pratt W.K. Digital image processing. Wiley-Interscience Publ., NY, 1978, 750 p. (Russ. ed.: Moscow, Mir, 1982).

2. Gonzalez R., Woods R. Digital image processing, 2002, 822 p. (Russ. ed.: M., Technosphere, 2005, 1072 p).

3. Soifer V.A., Sergeev V.V., Popov S.B., Myasnikov V.V. Theoretical foundations of digital image processing. Samara State Aerospace University S.P. Queen, 2000, 256 p.

4. Potapov A.A., Gulyaev Yu.V., Nikitov S.A., Pakhomov A.A., German V.A. The latest image processing techniques. M., 2008, 496 p. (in Russ.).

5. Alpatov B.A., Babayan P.V., Balashov O.E., Stepashkin A.I. Systems for automatic detection and tracking of objects. Image processing and management . M., 2008, 176 p. (in Russ.).

6. Yang Y., Zheng Q. Moving object detection for dynamic background scenes based on spatoiotemporal model. Advenced in Multimedia, 2017, vol. 2017, art. ID 5179013, 9 p. DOI: 10.1155/2017/5179013.

7. Sun P., Yuan G., Li D. An overview of moving object trajectory compression algoritms, Matematical Problems in Engineering, 2016, vol. 2016, art. ID 6587309, 13 p. DOI: 10.1155/2016/6587309.

8. Katulev A.N., Khramichev A.A., Yagolnikov S.V. Digital processing of 2D low-contrast images formed by an optoelectronic device in difficult background conditions. Detection, recognition, tracking of dynamic objects . M., 2018, 408 p. (in Russ.).

9. Borzov S.M. Detection of dynamic objects by space-time anomalies in video sequences. Autometry, 2013, vol. 49, no. 1, pp. 11–17 (in Russ.).

10. Potapov A.A. Fractals, fractional operators, and scaling — the basis of new methods for processing
information, synthesizing fractal radio systems, antennas, and impedances. Proc. Intern. Microwave & Telecomunication Conf., Crimea, Ukraine, pp. 39–46 (in Russ.).

11. Katulev A.N., Kolonskov A.A., Khramichev A.A., Yagolnikov S.V. An adaptive method and algorithm for detecting low-contrast objects by an optical-electronic device. 2014, Optical J., vol. 81, no. 2, pp.29–39 (in Russ).

12. Julier S.J., Uhlmann J.K. Unscented filtering and nonlinear estimation. Proc. IEEE, 2004, vol. 92, no. 3, pp. 401–422. Available at: : https://www.cs.ubc.ca/~murphyk/Papers/Julier_Uhlmann_mar04.pdf (accessed).

13. Potapov A.A. Fractals in radiophysics and radar. M., 2002, 664 p. (in Russ.).

14. Yilmaz А., Shafique К., Shah М. Target tracking in airborne forward-looking infrared imagery. Image and Vision Computing, 2003, no. 21, pp. 623–635. Available at: https://www.crcv.ucf.edu/papers/
yilmaz_ivc_2002.pdf (accessed). DOI: 10.1016/S0262-8856(03)00059-3.

15. Zhang Y., Chen S., Li M. The implementation of adaptive optics wavefront spot extraction on FPGA. Optical J., 2013, vol. 80, no. 1, pp. 68–74 (in Engl.).

16. Katulev A.N., Khramichev A.A. Wavelet-fractal-correlation algorithm for recognizing the type of a dynamic object detected by an optical-electronic device. Optical J., 2017, vol. 84, pp. 25–34 p. (in Russ.).

 

УДК 621.396

DOI: 10.15827/2311-6749.20.1.1

Программный комплекс обработки двумерных изображений для оптико-электронных
систем обнаружения, сопровождения и распознавания динамических объектов

А.А. Храмичев ¹ , к.т.н., с.н.с., генеральный директор

А.Ю. Козлов ¹ , к.т.н., доцент, старший научный сотрудник, rtisvko@rtisvko.ru

 

¹ АО «Радиотехнические и информационные системы воздушно-космической обороны»,
г. Тверь, 170041, Россия

Развиты теория и методы адаптивной оптимальной автоматической обработки изображений, формируемых оптико-электронными приборами при обнаружении, распознавании и сопровождении воздушных динамических объектов в сложных фоновых условиях.

В основу положены вейвлет-фрактально-корреляционные принципы обработки информации без использования априорных данных о текущей обстановке в зоне контролируемого оптико-электронным прибором пространства.

Решена проблема автоматического обнаружения, распознавания типа и сопровождения динамических объектов в сложных фоновых условиях. Построены алгоритмы обработки изображений по пространственно протяженным, малоразмерным и точечным слабоконтрастным кластерам пикселей фоноцелевых кадров. Представлена программная реализация комплексного алгоритма, являющегося вейвлет-фрактально-корреляционно-статистическим. Алгоритм обеспечивает в автоматическом режиме
при априорной неопределенности решение задач обнаружения и сопровождения динамических объектов на изображениях фоноцелевых кадров оптико-электронных приборов с последующим формированием информации с целью распознавания типа динамического объекта и выдачи для анализа текущего состояния контролируемой фоноцелевой обстановки.

Разработанные методы и алгоритмы в целом представляют новое направление в теории и практике цифровой обработки изображений в условиях априорной неопределенности.

Ключевые слова: оптико-электронный прибор, динамический объект, сигнал-изображение, фоноцелевой кадр, вейвлет-коэффициент, фрактальная размерность.

Благодарности: статья подготовлена в рамках выполнения госзадания Минобрнауки РФ, шифр 2.1777.2017/ПЧ.

Литература

1. Прэтт У.К. Цифровая обработка изображений; [пер. с англ.]. М.: Мир, 1982.

2. Гонсалес Р., Вудс Р. Цифровая обработка изображений. М.: Техносфера, 2005. 1072 с.

3. Сойфер В.А., Сергеев В.В., Попов С.Б., Мясников В.В. Теоретические основы цифровой обработки изображений. Самара: Изд-во СГАУ им. С.П. Королева, 2000. 256 с.

4. Потапов А.А., Гуляев Ю.В., Никитов С.А., Пахомов А.А., Герман В.А. Новейшие методы обработки изображений. М., 2008. 496 с.

5. Алпатов Б.А., Бабаян П.В., Балашов О.Е., Степашкин А.И. Системы автоматического обнаружения и сопровождения объектов. Обработка изображений и управление. М.: Радиотехника, 2008. 176 с.

6. Yang Y., Zheng Q. Moving object detection for dynamic background scenes based on spatoiotemporal model. Advenced in Multimedia, 2017, vol. 2017, art. ID 5179013, 9 p.

7. Sun P., Yuan G., Li D. An overview of moving object trajectory compression algoritms, Matematical Problems in Engineering, 2016, vol. 2016, art. ID 6587309, 13 p. DOI: 10.1155/2016/6587309.

8. Катулев А.Н., Храмичев А.А., Ягольников С.В. Цифровая обработка 2D слабоконтрастных изображений, формируемых оптико-электронным прибором в сложных фоновых условиях. Обнаружение, распознование, сопровождение динамических объектов. М.: Радиотехника, 2018. 408 с.

9. Борзов С.М. Обнаружение динамических объектов по прострнственно-временным аномалиям
в видеопоследовательностях // Автометрия. 2013. Т. 49. № 1. С. 11–17.

10. Потапов А.А. Фракталы, дробные операторы и скейлинг–основа новых мeтодов обработки
информации, синтеза фрактальных радиосистем, антенн и импедансов // Microwave & Telecomunication: тр. Междунар. науч. конф. Крым, 2010. С. 39–46.

11. Катулев А.Н., Колонсков А.А., Храмичев А.А., Ягольников С.В. Адаптивный метод и алгоритм обнаружения малоконтрастных объектов оптико-электронным средством // Оптический журнал. 2014. Т. 81. № 2. С. 29–39.

12. Julier S.J., Uhlmann J.K. Unscented filtering and nonlinear estimation. Proc. IEEE, 2004, vol. 92, no. 3, pp. 401–422. URL: https://www.cs.ubc.ca/~murphyk/Papers/Julier_Uhlmann_mar04.pdf (дата обращения:).

13. Потапов А.А. Фракталы в радиофизике и радиолокации. М.: Логос, 2002. 664 с.

14. Yilmaz А., Shafique К., Shah М. Target tracking in airborne forward-looking infrared imagery. Image and Vision Computing, 2003, no. 21, pp. 623–635. URL: https://www.crcv.ucf.edu/papers/yilmaz_ivc_2002.pdf (дата обращения:). DOI: 10.1016/S0262-8856(03)00059-3.

15. Zhang Y., Chen S., Li M. The implementation of adaptive optics wavefront spot extraction on FPGA // Оптический журнал. 2013. Т. 80. № 1. С. 68–74 (англ.).

16. Катулев А.Н., Храмичев А.А. Вейвлет-фрактально-корреляционный алгоритм распознавания типа динамического объекта, обнаруживаемого оптико-электронным прибором // Оптический журнал. 2017. Т. 84. № 4. С. 25–34.