Прогнозирование является одним из наиболее важных моментов в принятии управленческих и организационных решений в большинстве сфер человеческой деятельности. Качественное прогнозирование процессов, будь то экономические процессы внутри государства или маленькой компании, социальные процессы и многие другие, позволяет принимать эффективные и своевременные решения, а также накапливать опыт, который в дальнейшем позволит повысить качество и самого прогноза, имеющего фундаментальное значение для многих процессов принятия решений в планировании, разработке стратегий, построении политики, а также в управлении поставками и ценах акций. Как таковое прогнозирование является областью, в которую вложено немало усилий в прошлом, остается важной и активной областью человеческой деятельности в настоящем и продолжит развиваться в будущем. Обзор исследовательских потребностей в прогнозировании представлен работе [1].
Стремительное развитие информационных технологий и повсеместное внедрение их во все большее количество сфер человеческой деятельности позволяют получать данные о развитии широчайшего спектра процессов, нуждающихся в последующем анализе и прогнозировании. Ежедневно накапливается огромное количество данных, включающих в себя экономические, производственные и другие показатели, существенно увеличивающие объем входных данных, необходимых для задачи прогнозирования.
Но в то же время растут и требования к точности прогнозировании. Вместе с тем, несмотря на огромное количество информации, растет степень нелинейности, нелогичности и зашумленности данных. Кризисные явления, современная политическая и экономическая ситуации в мире влекут за собой глобальные изменения во всех сферах деятельности человека, что существенно затрудняет прогнозирование временных рядов на основе только лишь исторических данных.
В развитии и будущих изменениях временных рядов имеет место рефлексивность между событиями, их участниками и собственно прогнозируемым процессом (временным рядом), между исследователем и исследуемым процессом [2]. Теория рефлексивности в экономическом мире говорит о том, что возникшая ситуация действует на поведение самих участников процесса, а их мышление и поведение действуют на развитие ситуации, участниками которой они являются [3]. Понятно, что, пользуясь одним лишь инструментом прогнозирования временных рядов, каким бы мощным он ни был, невозможно отразить и учесть ситуацию и события, воздействующие на исследуемый процесс, так, как, допустим, нейронная сеть работает с историческими данными. Практическим выходом из положения является разработка таких методов, которые бы могли оперировать как с причинно-следственными отношениями между событиями и прогнозируемым процессом, так и с числовыми значениями временного ряда, его историческими данными. Поэтому целесообразна разработка гибридной системы прогнозирования, способной оперировать как качественными, так и количественными данными.
В настоящей работе предлагается новая гибридная модель прогнозирования временных рядов, основанная на нечетких реляционных когнитивных картах и гибридной нейро-нечеткой сети с регрессионным анализом.
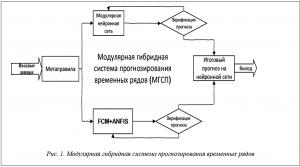
Модулярная гибридная система прогнозирования временных рядов
Разработанная система прогнозирования базируется на модулярной архитектуре, придающей системе дополнительную устойчивость: даже если один из модулей выходит из строя, остальные продолжают выполнять свою работу.
Сама система имеет три основных модуля, отвечающих за задачу прогнозирования. Гибридная нейро-нечеткая сеть выполняет прогноз временного ряда на основе численных показателей и дает так называемый количественный прогноз, результаты которого проходят через систему верификации (оценки адекватности прогноза), если прогноз соответствует необходимой точности, то он передается на следующий модуль. Параллельно с нейро-нечеткой сетью работает модуль с нечеткой когнитивной картой, который получает на вход данные о событийном влиянии на временной ряд, строится когнитивная карта, в которой учитываются все факторы влияния на конкретный прогнозируемый показатель. На выходе когнитивная карта дает прогноз с вероятностью его выполнения, то есть с консонансом фактора, который говорит о том, выполнится прогноз или нет. Далее все данные, полученные с данных модулей, поступают на третий модуль, работающий на основе нейронной сети, который агрегирует информацию, полученную с предыдущих модулей, и выдает итоговый прогноз. На рисунке 1 представлена схема системы прогнозирования.
Далее более подробно остановимся именно на прогнозировании на основе нечетких когнитивных карт и их обучении, так как прогнозам на нейро-нечетких сетях посвящено достаточно большое количество исследований [4], а с когнитивными картами ситуация несколько иная.
Прогнозирование временных рядов на основе нечетких когнитивных карт
Временным рядом управляют две основные силы – время и события, влияющие на изменение с течением времени значений временного ряда. Большинству подобных событий свойственна некоторая неопределенность. Каждому значению временного ряда можно поставить в соответствие нечеткую переменную с некой функцией принадлежности. В этой связи наибольший интерес для данного исследования представляют методы, основанные на теории нечетких множеств. Лотфи Заде в 1965 году ввел понятие нечеткого множества, благодаря которому можно описывать качественные, нечеткие понятия и знания об окружающем мире, а в дальнейшем оперировать ими для получения новой информации [5]. Применение данного понятия позволяет формализовать лингвистическую информацию для построения математических моделей [6]. В основе понятия нечеткого множества лежит суждение, что элементы, составляющие данное нечеткое множество, а также обладающие общими свойствами, могут обладать им и, следовательно, принадлежать к этому множеству в различной степени. В данном случае высказывания вида «такой-то элемент принадлежит данному множеству» теряют смысл, так как еще нужно указать степень принадлежности к этому множеству и его свойствам [7].
Чтобы иметь возможность оперировать событиями, влияющими на временной ряд, а событий может быть достаточно много и каждое может быть связано друг с другом, имеет смысл использовать нечеткие когнитивные карты. Они позволяют построить причинно-следственные связи между событиями и построить качественный прогноз развития события, основываясь на силе влияния одного события на другое.
Сама когнитивная карта представляет собой ориентированный граф, вершины которого – факторы ситуации, а взвешенные дуги – причинно-следственные отношения, вес которых отражает силу влияния факторов ситуации. Направленным дугам графа приписывается знак «+» или «–», то есть они могут быть положительными или отрицательными. Положительная связь означает, что увеличение значения фактора-причины приводит к увеличению значения фактора-следствия, а отрицательная дуга означает, что увеличение значения фактора-причины приводит к уменьшению значения фактора-следствия.
Задачи, решаемые с помощью когнитивных карт, заключаются в нахождении и оценивании влияний факторов ситуации и в получении на основе вычисленных влияний прогнозов развития ситуации.
В настоящее время для вычисления влияний и прогнозов развития ситуации широкое применение находят нечеткие когнитивные карты, предложенные Б. Коско [8]. В нечетких когнитивных картах сила влияния между факторами задается с помощью лингвистических значений, выбранных из упорядоченного множества возможных сил влияний, а значения факторов, их приращения также задаются в лингвистическом виде и выбираются из упорядоченных множеств возможных значений фактора и его возможных приращений – шкал факторов и шкал приращений.
Для построения когнитивной карты, отражающей динамические свойства наблюдаемой ситуации, необходимо определить шкалы значений факторов и их приращений.
Для построения шкалы фактора определяется и структурируется множество лингвистических значений фактора. При определении лингвистических значений используются абсолютные значения фактора, а не его оценки типа «большой», «средний», «маленький». Например, лингвистическое значение температуры может быть следующим – «так горячо, что едва можно приложить ладонь» или значение «так холодно, что рука сразу замерзает», а не просто «горячо» или «холодно». При таком определении лингвистических значений факторов ситуации задается объективный эталон его значения – опорная точка.
Задание объективного эталона значения фактора облегчает работу экспертов при определении силы влияния факторов и уменьшает экспертные ошибки.
Задача прогноза сводится к макстриангулярной композиции матрицы весов и вектора начальных приращений признаков.
Этот алгоритм работает для положительно определенных матриц, в то время как в данном случае элементы матрицы смежности и векторов приращений могут принимать отрицательные и положительные значения.
Используется следующее правило преобразования матрицы смежности 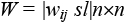 с положительными и отрицательными элементами к положительно определенной двойной матрице
с положительными и отрицательными элементами к положительно определенной двойной матрице 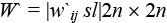 [6]:
[6]:
если (wij sl) > 0, то w`i(2j-1) s(2l – 1) = wij sl,w`i(2j) s(2l) = wij sl;
если (wij sl) < 0, то w`i(2j) s(2l) = –wij sl,w`i(2j) s(2l –1) = – wij sl.
Начальный вектор приращений P(t) и вектор прогнозных значений признаков P(t + 1) в этом случае должны иметь размерность 2n. Правило получения начального вектора приращений P`(t) размерности 2n из вектора начальных приращений P(t) размерности n следующее:
если pij(t) > 0, то p`i(2j – 1)(t) = pij(t), p`i(2j)( t) = 0;
если pij(t) < 0, то p`i(2j )(t) = pij(t), p`i(2j – 1)(t) = 0.
В векторе P`(t) = (p11–, p 11+, …, pnm–, pnm +) значение признака fij характеризуют два элемента: элемент с индексом 2j характеризуют положительное pij +, а с индексом 2j – 1 – отрицательное pij –, приращение признака fij.
Тогда двойной вектор приращений P`(t + 1) для положительно определенной матрицы W` определяется с помощью следующего уравнения:
P `(t + 1) = P`(t) °W`,
где для вычисления элемента вектора P`(t + 1) используется правило:
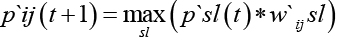
Элементы векторов приращений значений признаков, полученные в последовательные моменты времени P`(t + 1), …,P`(t + n), после транспонирования представляются в виде блочной матрицы:
Pt = |P`(t + 1)T, …, P`(t + n)T|.
Строки этой матрицы – это значения приращения одного признака в последовательные моменты времени, столбцы – значения приращения всех признаков в момент времени, соответствующий выбранному столбцу. Матрица Pt называется матрицей приращений и используется при работе алгоритмов объяснения прогнозов развития ситуации [7].
Метод получения прогноза
Задано множество факторов ситуации F = {fj}, j = 1, …, m; Zj = {zjk} – упорядоченное множество лингвистических значений i-го фактора, k – номер лингвистического значения, и определены шкалы всех факторов Xi. Экспертным путем определяется когнитивная карта (F, W), где F – множество вершин – факторов ситуации, W = | wij| – матрица смежности, и начальное состояние ситуации как вектор значений всех факторов ситуации X(0) = ( x10, …, xm0). Определен начальный вектор приращений факторов ситуации P(t)=( p1, …, pm).
Необходимо найти векторы состояния ситуации X(t), X (t + 1), …, X (t + n) и векторы приращения состояния ситуации P(t), P( t + 1), …, P(t + n) в последовательные дискретные моменты времени t, t + 1, …, t + n, где t – номер шага (такта) моделирования.
Прогноз развития ситуации определяется с помощью матричного уравнения:
P (t + 1) = P(t) ° W,
где (°) – правило max-product: 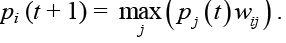
Элемент вектора прогноза развития ситуации 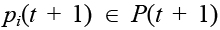 представляется парой:
представляется парой: 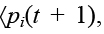
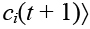 , где pi (t + 1) – значение приращения фактора, ci (t + 1) – консонанс значения фактора. Когнитивный консонанс о значении фактора используется для характеристики уверенности субъекта в результатах моделирования. При ci(t) ≈ 1 уверенность субъекта в приращении фактора pi(t) максимальна, а при ci (t) ≈ 0 минимальна.
, где pi (t + 1) – значение приращения фактора, ci (t + 1) – консонанс значения фактора. Когнитивный консонанс о значении фактора используется для характеристики уверенности субъекта в результатах моделирования. При ci(t) ≈ 1 уверенность субъекта в приращении фактора pi(t) максимальна, а при ci (t) ≈ 0 минимальна.
Состояние ситуации в последовательные моменты времени будем определять парой: 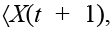
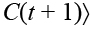 , где X(t + 1) = X(t) + P(t + 1) – вектор состояния ситуации (элемент этого вектора xi(t + 1) = xi( t) + pi(t + 1)), когнитивный консонанс значения
, где X(t + 1) = X(t) + P(t + 1) – вектор состояния ситуации (элемент этого вектора xi(t + 1) = xi( t) + pi(t + 1)), когнитивный консонанс значения 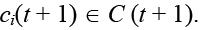
Правдоподобный прогноз развития ситуации в этом случае будем определять парой 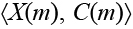 , где X(m)= (x1(m), …, xm (m)) – вектор значений факторов ситуации в момент t =m; C(m) = (c1(m), …, cm(m)) – вектор консонанса значений факторов ситуации в момент t = m.
, где X(m)= (x1(m), …, xm (m)) – вектор значений факторов ситуации в момент t =m; C(m) = (c1(m), …, cm(m)) – вектор консонанса значений факторов ситуации в момент t = m.
Способы интерпретации нечетких когнитивных карт
Существует довольно большое количество способов интерпретации нечетких когнитивных карт. Рассмотрим наиболее интересные и новые из них. Большинство этих способов расширяют возможности нечеткой когнитивной карты за счет того, что снимают ограничение на моделирование немонотонных и несимметричных нечетких отношений.
В [9] рассматривается подход, основанный на использовании нечетких мер (fuzzy measures).
Нечеткая мера (понятие введено Мичио Сугэно в 1974 году) может рассматриваться как обобщение классической вероятностной меры. Нечеткая мера g над множеством X (рассматриваемый универсум с подмножествами E, F...) удовлетворяет следующим условиям, когда X конечно.
1. Если E – пустое множество, то g(E) = 0.
2. g(X) = 1.
3. Если E – подмножество F, то g(E) < g(F).
Применение правил вывода, основанных на нечетких мерах, демонстрируется на примере решения проблемы принятия решений в слабоструктурированной проблемной области очистки воды в распределительных системах.
Обобщение использования t- и s-норм с помощью усредняющих операторов (ordered weighted averaging operators, OWA) предложено в [10]. В этой работе отмечается, что в классическом случае s(x, y) ≥ max(x, y) (максимум – минимальная s-норма), а t(x, y) ≤ min( x, y) (минимум – максимальная t-норма), и предлагается использование некоторой функции t(x, y) ≤ a(x, y) ≤ s( x, y), называемой OWA-оператором.
Нечеткие когнитивные карты, основанные на нечетких правилах, рассматриваются в [11]. В данной работе нечеткие когнитивные карты представляются в виде набора концептов и набора нечетких правил (вместо классических связей). Отношения между концептами («похожи», «противоположны», «влечет за собой» и т.д.) выражаются в виде нечетких правил и логических операторов («и», «или» и т.д.). База правил (fuzzy rulebase) состоит из набора утверждений вида Если ... То. Нечеткие когнитивные карты, основанные на нечетких правилах (Rule based нечеткой когнитивной карты, RBнечеткой когнитивной карты), в отличие от обычных нечетких когнитивных карт, в большей степени схожи с другими классами нейронечетких систем, поскольку возможности их не ограничены операциями с нечеткими числами, но включают в себя также классические механизмы нечеткого вывода.
Подход, связанный с отказом от простого умножения матрицы весов на значения концептов, использующийся в имитационном моделировании карт, основанных на правиле sum-product, рассматривается в [12]. Важным преимуществом когнитивных карт, основанных на мягкой логике (pliant logic), является их временной фактор: вместо фиксированных значений весов связей в карте авторы работы используют функции, зависящие от времени. В работе сравниваются подход, основанный на фиксированных нечетких правилах, и подход, реализующий меняющуюся во времени мягкую логику, и демонстрируется, что второй подход гораздо гибче моделирует ситуации реального мира.
Обучение нечетких когнитивных карт
Как уже говорилось, нечеткие когнитивные карты имеют существенный недостаток – необходимость кропотливой работы эксперта по выявлению причинно-следственных связей между концептами в системе, а также по настройке весов этих связей.
Большинство используемых в системах поддержки принятия решений, а также разработанных в результате различных предметных исследований нечетких когнитивных карт имеют плотность порядка 15–30 % [8] и размер 7–10 концептов. Это означает, что для правильной настройки этих карт экспертам приходится довольно точно оценить порядка 7–30 связей. Если в случае с 7 связями эта задача выглядит разрешимой, то в случае 30 связей процесс настройки нечеткой когнитивной карты становится нетехнологичным.
С этой целью используют автоматическую подстройку весов нечеткой когнитивной карты. Для этого применяются различные виды обучающих алгоритмов, основанных на так называемых мягких вычислениях.
Задача обучения формулируется как минимизация ошибки результата прогнозирования нечеткой когнитивной карты. Ошибка прогнозирования оценивается как погрешность между прогнозными показателями карты и реальными значениями концептов, известных из исторических наблюдений.
В зависимости от того, что понимается под прогнозированием, задача обучения формулируется по-разному.
В данной работе рассматриваются две задачи прогнозирования. Первая связана с моделированием карт, основанных на правиле max-product, и формулируется как определение значений концептов в разные такты времени. Вторая формулируется согласно [13] и [14] как задача определения приращений концептов, возникающих в карте при внесении в нее «возмущений» – изначального вектора приращений концептов.
Для первой задачи было разработано несколько вариантов алгоритмов обучения. В [15] описывается применение генетических алгоритмов для обучения нечеткой когнитивной карты, рассматриваются алгоритмы с разными наборами параметров и тестируются на реальных и синтетических когнитивных картах с разными характеристиками (количество концептов, плотность). Другой подход связан с применением нейронных сетей (этот подход более подробно будет описан в следующем разделе.
Для второй задачи до сих пор не были предложены алгоритмы обучения. В данной работе для решения этой задачи будет предложен и реализован генетический алгоритм обучения.
Нейросетевой подход к обучению
Нейронные сети дают возможность обучения нечетких когнитивных карт. Смысл в том, чтобы в процессе обучения позволить весам в нечеткой когнитивной карте меняться таким образом, как если бы они были весами связей (синапсов) в нейронной сети. Концепты в данном случае – это нейроны в сети.
Уровень активности концепта (нейрона) определяется как взвешенная сумма сигналов от других концептов на предыдущей итерации, нормированная с помощью функции активации (например, сигмоидальной функции). Это полностью соответствует «классическому» подходу к построению нечеткой когнитивной карты. Поскольку нет никаких разногласий в принципах функционирования нейронной сети и нечеткой когнитивной карты, для обучения нечеткой когнитивной карты предлагается широко известный метод обучения нейронной сети – метод обратного распространения ошибки (back propagation).
В классическом варианте метод предполагает «движение» ошибки от выходного слоя к входным через все промежуточные слои, причем на каждом слое определяется «вес» каждой связи в общей ошибке сети. Общая ошибка сети задается формулой
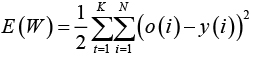
где o(i) – прогнозное значение концепта в момент времени t, а y(i) – реальное (историческое) значение. «Вклад» каждого концепта в общую ошибку определяется как частная производная по этому концепту от ошибки:
.jpg)
где neti определяется согласно следующей формуле:
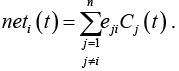
Подстройка весов осуществляется по формуле
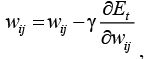
где 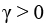 – скорость обучения.
– скорость обучения.
Данный подход подробно рассматривается и реализуется в [16] (проект Woodstrat – модель инвестиций). Показано, что нейронный подход может успешно применяться для автоматической настройки весов нечеткой когнитивной карты, работающей по правилу sum-product, при репрезентативном наборе обучающих данных.
Обучение генетической карты с помощью генетического алгоритма
Предположим, что имеется набор из 3N строк исторических данных (далее – материал обучения) о состоянии концептов в системе. С точки зрения задачи прогнозирования на основе приращений концептов (см. «Метод получения прогноза») приращения концептов от i-й итерации к (i + 1)-й итерации составят исходный вектор приращений. В этом случае нечеткая когнитивная карта должна показать, что при подобном исходном векторе приращений значения концептов изменятся таким образом, что результирующие их приращения приведут к значениям на (i + 2)-й итерации.
Пусть Ai(t) – значение концепта в момент времени t. Исходя из спецификации материала обучения, данной выше, будем рассматривать тройки строк: Ai(t), Ai(t + 1), Ai(t + 2).
Определим , 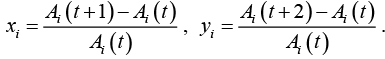 . Здесь – это исходные векторы приращений, y – результирующие векторы приращений.
. Здесь – это исходные векторы приращений, y – результирующие векторы приращений.
Пусть oi(t) – приращение ei, полученное в результате прогноза на исходном векторе x(t).
Задача обучения состоит в минимизации ошибки нечеткой когнитивной карты, но с учетом введенных в данном параграфе значений x, y, o.
Для решения задачи обучения предлагается генетический алгоритм. В качестве хромосомы выделяется одномерный массив значений, в который разложен двумерный массив весов нечеткой когнитивной карты. Каждое значение в этом массиве называется геном. Определим основные шаги алгоритма.
1. Для всех ненулевых значений весов исходной карты определяется новое ненулевое значение веса, задаваемое малым случайным числом (знак не важен). Исходные ненулевые значения весов определяются экспертом (ненулевое значение может быть любым, его единственное предназначение – указание о том, что, по мнению эксперта, между двумя выбранными концептами существует причинно-следственная связь).
2. Пункт 1 повторяется PopulationSize раз. Таким образом, формируется первоначальная популяция случайных решений.
3. Определяется функция приспособленности (fitness function) для каждой хромосомы (о виде функции приспособленности речь пойдет далее).
4. Определяется пул родителей по методу «рулетки».
5. В пул родителей добавляются «элитные особи». Под элитными особями в генетических алгоритмах подразумеваются особи, показавшие наилучшее значение функции приспособленности на нескольких последних поколениях (по одной особи от поколения).
6. Происходит скрещивание хромосом, попавших в пул родителей. Скрещивание хромосом A и B происходит следующим образом. Случайным образом определяется граница скрещивания . Обозначим Al+ часть хромосомы A, состоящую из генов, расположенных начиная с l, и Al– – часть хромосомы, расположенную до l. Тогда результатом скрещивания будут две хромосомы: Al–Bl+ и Bl–Al+. Вероятность скрещивания определена заранее. Если скрещивания не происходит, обе родительские хромосомы без изменений переходят в популяцию потомков.
7. Из потомков, полученных на шаге 6, формируется новая популяция (размер ее точно совпадает с размером популяции на предыдущем шаге алгоритма).
8. Происходят мутации в популяции потомков. При мутации выбирается случайный ген и заменяется на новое случайное значение. Вероятность мутации определена заранее. Если мутации не происходит, хромосома переходит на следующую итерацию алгоритма неизменной.
9. Определяются следующие параметры поколения: элитная особь (особь, обладающая наилучшим значением степени приспособленности) для сохранения ее генофонда; среднее значение приспособленности популяции (имеет значение только для оценки сходимости алгоритма); значение приспособленности элитной особи.
10. Если значение приспособленности элитной особи больше заранее заданного значения максимальной приспособленности, алгоритм останавливается и выбранная хромосома раскладывается в матрицу смежности нечеткой когнитивной карты (обучение считается завершенным). Иначе происходит переход на шаг 3.
Концепция элитных особей была введена в алгоритм для ускорения сходимости алгоритма. Количество элитных особей взято равным 60, в то время как размер популяции равен 100 (таким образом, на каждом шаге после 60-го поколения только 40 хромосом из текущей популяции имеют шансы на скрещивание – остальное заполняет элитный генофонд, доставшийся в наследство от предыдущих популяций).
Максимальное значение приспособленности определено как 0,99. Результаты обучения округляются до сотых долей.
Вероятность скрещивания определена как 0,9, а вероятность мутации – 0,5. Столь высокое значение вероятности мутации (обычно нехарактерное для генетических алгоритмов) в данном случае оправдано, так как мутации вносят генетическое разнообразие в популяцию. При этом, поскольку используется элитный генофонд, нет риска безвозвратной «потери» полезных генов, доставшихся от предыдущих поколений.
Гибридный подход к прогнозированию на основе нечетких когнитивных карт и нейронных сетей
Использование данного подхода позволяет повысить точность прогнозирования благодаря использованию в качестве входных данных нейронной сети узлы нечеткой когнитивной карты. Не секрет, что большое влияние на точность прогноза влияет выборка данных, на которой строится прогноз.
Подход имеет две основные стадии [17]. На первой стадии разрабатывается модель нечеткой когнитивной карты по историческим данным временных рядов с помощью генетического алгоритма обучения. Описать поэтапно первую стадию можно следующим образом.
1. Инициализация нечеткой когнитивной карты по историческим данным временных рядов.
2. Построение оптимизированной нечеткой когнитивной карты (выбирая наиболее значимые концепты и их соединения) с использованием генетического алгоритма.
3. Тестирование нечеткой когнитивной карты на основе нормализованных проверочных данных.
Используя концепты нечеткой когнитивной карты для определения входов для нейро-нечеткой сети [18] для повышения точности прогнозирования. Вторая стадия состоит из следующих шагов.
1. Повышение точности прогнозирования, используя отобранные входные данные – концепты разработанной когнитивной карты.
2. Обучение нейронной сети.
3. Тестирование полученной нейронной сети на тестовых данных.
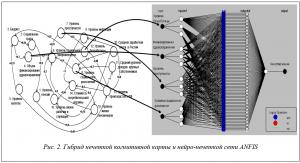
Подобный пример, изображенный на рисунке 2, представляет процесс прогнозирования такого показателя, как качество жизни населения. Использование когнитивной карты в этой ситуации является наиболее целесообразным по следующей причине: чтобы построить качественный прогноз данного показателя, как многих других, необходимо выделить наиболее влияющие на индикатор факторы. Когнитивная карта наилучшим образом помогает решить подобную задачу и тем самым подать на входы нейронной сети подготовленные данные концептов когнитивной карты.
Заключение
Результаты данной работы показывают эффективность создания гибридных систем как для задачи принятия решений, так и для задачи прогнозирования временных рядов. Представлена интегрированная гибридная модель поддержки принятия решений и прогнозирования на основе нечетких когнитивных карт. Подобное решение послужило фундаментом для разработки системы прогнозирования временных рядов, которая уже объединила в себе данный метод и методы искусственного интеллекта в задаче анализа данных. Представлена новая модель модулярной системы прогнозирования временных рядов.
Подробно рассмотрен один из модулей данной системы, содержащий в себе гибридную подсистему, состоящую из комбинации нечеткой когнитивной карты и нейро-нечеткой сети ANFIS. Детально рассмотрассмотрен модуль, включающий когнитивную карту. Представлен и описан генетический алгоритм обучения когнитивной карты, а также его возможности в задачах прогнозирования.
Литература
1. Armstrong J.S. Research needs in forecasting. Intern. Jour. of Forecasting, 1988, no. 4, pp. 449–465.
2. Лефевр В.А. Исходные идеи логики рефлексивных игр // Проблемы исследования систем и структур: матер. конф. М.: АН СССР, 1965.
3. Soros G. The alchemy of finance. John Wiley & Sons, 2003, 391 p.
4. Yarushev S.A., Averkin A.N. Review of studies on time series forecasting based on hybrid methods, neural networks and multiple regression // Программные продукты и системы. 2016. № 1. С. 75–83 (англ.).
5. Беллман Р., Заде Л. Принятие решений в расплывчатых условиях. В кн.: Вопросы анализа и процедуры принятия решений. М.: Мир, 1976. С. 172–215.
6. Ротштейн А.П., Штовба С.Д. Нечеткая надежность алгоритмических процессов. Винница: Континент-Прим, 1997. 142 с.
7. Аверкин А.Н., Батыршин И.З., Блишун А.Ф., Силов В.Б., Тарасов В.Б. Нечеткие множества в моделях управления и искусственного интеллекта; [под ред. Д.А. Поспелова]. М.: Наука, 1986. 312 с.
8. Kosko B. Fuzzy cognitive maps. Intern. Jour. Man-Machine Studies, 1986, vol. 24, no. 1, pp. 65–75.
9. Sadiq R., Kleiner Y., Rajani B. Interpreting fuzzy cognitive maps (FCMs) using fuzzy measures to evaluate water quality failures in distribution networks. Joint Intern. Conf. Computation in Civil and Building Engineering (ICCCBE XI), Montreal, QC, 2006, pp. 1–10.
10. Zhenbang Lu, Lihua Zhou. Advanced Fuzzy Cognitive Maps Based on OWA Aggregation. Intern. Jour. Computational Cognition, 2007, vol. 5, no. 2, pp. 31–34.
11. Carvalho J.P., Tome J.A.B. Rule Based Fuzzy Cognitive Maps and Fuzzy Cognitive Maps – A comparative study. Proc. 18th Intern. Conf. NAFIPS99, 1999, pp. 115–119; DOI: 10.1109/NAFIPS.1999.781665.
12. Dombi J., Dombi J.D. Cognitive maps based on pliant logic. I.J. of Simulation, 2003, vol. 6, no. 6.
13. Силов В.Б. Принятие стратегических решений в нечеткой обстановке. М.: ИНПРО-РЕС, 1995.
228 c.
14. Кулинич А.А. Разработка принципов и методов построения программных систем поддержки принятия решений в слабо структурированных ситуациях на основе моделирования знаний эксперта: дис… канд. технич. наук. М.: ИПУ РАН, 2003. 150 с.
15. Stach W., Kurgan L., Pedrycz W., Reformat M. Genetic learning of fuzzy cognitive maps. Fuzzy Sets and Systems, 2005, no. 153, pp. 371–401.
16. Carlsson C., Fuller R. Adaptive fuzzy cognitive maps for hyperknowledge representation in strategy formation process. Proc. Intern. Panel Conf. on Soft and Intelligent Computing, Technical Univ. of Budapest, 1996, pp. 43–50.
17. Papageorgiou E.I., Poczęta K. A two-stage model for time series prediction based on fuzzy cognitive maps and neural networks. Neurocomputing, 2017, vol. 232, pp. 113–121.
18. Averkin A. N., Yarushev S. Hybrid approach for time series forecasting based on ANFIS and Fuzzy Cognitive Maps. Proc. Intern. Conf. SCM2017, IEEE, 2017, pp. 379–381.
Comments