Проблема выбора сопровождает человеческую деятельность во всех сферах общественной жизни, и от качества ее решения во многом зависит дальнейшая судьба того или иного начинания или проекта. Однако если в гуманитарных областях человек вынужден сам полностью выполнять процедуру анализа и выбора, то в ряде прикладных областей (технических, экономических и других) это уже способны делать информационные системы, в основу которых положены методы анализа, базирующиеся на построении моделей предметной области [1, 2], интеллектуально-экспертных подходах [3]. В то же время заложенные в их основу методы анализа можно отнести и к их недостаткам ввиду сложности самого процесса моделирования, требующего большой подготовительной работы и дальнейшей проверки адекватности модели. Поэтому в ряде случаев при оценке вариантов решения той или иной проблемы выгоднее сразу оценивать их по какому-либо набору критериев.
При относительно небольшом наборе критериев и альтернатив процесс выбора может и не представлять больших трудностей, однако в противном случае обоснование выбора уже не может обойтись без применения специальных методов. Например, оценка оптимальности стратегии управления проектами осуществляется по девяти критериям [4], которые носят качественный характер и плохо структурированы, а потому не поддаются однозначному определению за счет проведения измерений. В этих условиях целесообразны разработка и применение методов выбора альтернатив на основе «мягких» вычислений, позволяющих принимать приближенные решения на основе методов вычислительного интеллекта [5, 6].
Совершенствование одного из методов выбора альтернатив было обусловлено необходимостью обоснованного применения того или иного алгоритма решения обратных задач, возникающих при управлении сложными техническими объектами. В упрощенной трактовке в таких задачах требуется получить описание входного сигнала по имеющемуся наблюдению выходного сигнала объекта. Примером таких задач могут быть так называемые инструментальные задачи, в которых требуется восстановить сигнал по результатам показаний измерительных приборов. В свою очередь, обратные задачи относятся к классу некорректных задач, имеющих различные постановки и методы решения [7, 8].
Большая часть методов решения обратных задач построены на различных способах регуляризации, имеют свои ограничения и далеко не всегда применимы на практике [7]. Значительно менее требовательны к ограничениям на применимость методы решения обратных задач, основанные на аппроксимационном подходе [9] и интеллектуальных методах с применением нейро-нечетких алгоритмов калмановской фильтрации [10, 11]. Однако здесь встает задача – какой из этих методов выбрать применительно к конкретной практической постановке, основываясь на оценках каждого метода по нескольким критериям.
Учитывая, что применение того или иного алгоритма решения обратной задачи к данному объекту и предметной области зависит и от опыта исследователя, а критерии могут носить не только количественный, но и качественный характер, выбор был сделан в пользу метода выбора альтернатив на основе нечеткого отношения предпочтения [6]. Метод базируется на применении методов нечеткой логики и отвечает всем свойствам классического алгоритма, в том числе свойству детерминированности. Однако именно это свойство может в рассматриваемом методе нарушаться при незначительных изменениях значений функций принадлежности, что весьма возможно, учитывая субъективизм при их задании для конкретных переменных. Можно сказать, что таким образом проявляется вычислительная устойчивость или неустойчивость алгоритма [12]. Следует отметить, что данная ситуация характерна для некорректно поставленных задач, в которых небольшое изменение исходных данных может приводить к решению, не применимому на практике [13]. В этих условиях становится актуальной задача оценки чувствительности используемого метода выбора альтернатив к вариациям исходных данных. Подобные задачи всегда приходится решать для обоснования «устойчивости» принимаемого решения в различных прикладных областях [14, 15].
Алгоритм метода выбора альтернатив состоит из нескольких этапов. На первом этапе выбираются варианты решения задачи и критерии, которые используются для оценки каждого варианта. Набор вариантов решения обратной задачи Vj обозначается матрицей
V = {V1, V2, …, Vm},
а набор критериев Ci матрицей
C = {C1, C2, …, Cn}.
На втором этапе выполняется количественная оценка вариантов (альтернатив) по критериям с помощью задания функций принадлежности. В результате получаем матрицу
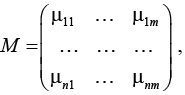 (1)
(1)
где mij - значение функции принадлежности для j-й альтернативы по i-му критерию.
Учитывая, что оценочное сравнение методов попарно дает более корректные с точки зрения объективности результаты, чем одновременное сравнение всех методов между собой, на основании (1) на третьем этапе по каждому критерию формируются матрицы попарных отношений предпочтения Pj на множестве M. Затем формируется подмножество недоминируемых альтернатив со значениями функций принадлежности:
![]()
где
![]() (2)
(2)
На четвертом этапе вычисляются элементы матриц D1, являющихся пересечением матриц попарных отношений предпочтения:
![]()
а далее матрица-строка нечеткого подмножества недоминируемых альтернатив:
![]()
На пятом этапе учитываются веса критериев wi, удовлетворяющие условию
![]()
и вычисляется еще одно нечеткое отношение D2:
![]()
На шестом этапе аналогично проводится расчет матрицы-строки нечеткого подмножества недоминируемых альтернатив для взвешенных критериев:
![]()
и находится матрица пересечения нечетких множеств:
![]() (3)
(3)
Номер максимального элемента в строке mнд будет соответствовать наилучшей альтернативе по заданным критериям.
На седьмом этапе предложено выполнить расчет чувствительности представленного алгоритма к вариациям функций принадлежности m ij в (1), так как именно эти значения отражают субъективный взгляд на возможности различных альтернатив применительно к конкретной предметной области.
Обозначим верхнюю границу диапазона изменения какого-либо параметра х через х+, а нижнюю х–. Чувствительность i-го критерия по j-й альтернативе будем вычислять в соответствии с выражением
![]() (4)
(4)
Выражение (4) позволяет сделать вывод о том, меняется ли выбор в зависимости от изменения значений функций принадлежности или нет. В отличие от принятых в теории систем выражений для чувствительности в данном случае нельзя судить о том, во сколько раз меняется выходная величина при изменении входной, так как важен только факт изменения решения (выбора альтернативы). Применение (4) в методе выбора недоминируемых альтернатив на основе нечеткого отношения предпочтения позволит убедиться в том, насколько «устойчивым» или обоснованным является выбор именно этой альтернативы при изменении функций принадлежности в (1). Важным при этом выборе должен быть тот факт, что относительно небольшие изменения значений функций принадлежности в (1) не должны приводить к изменению решения.
При наличии n критериев, m альтернатив и двух уровней значений функций принадлежности (х+, х–) всего возможных сочетаний уровней их значений будет N=2nm, то есть потребуется достаточно большое число расчетов, чтобы получить результаты выбора при каждом сочетании значений критериев. Однако такое число расчетов выполнять нет необходимости, так как будет проявляться противоречие между точностью исходных данных и точностью модели (алгоритма выбора), ведь исходные данные представляют собой значения функций принадлежности нечетких переменных, которые определяются субъективно. Кроме того, набор критериев может не отражать должной полноты своего набора для идеального выбора. В этих условиях для повышения степени уверенности в принятом решении (принятии данной альтернативы) будет оправданным ограничиться проверкойsij для изменения значений критериев в диапазонах [ х+, х–] и получения матрицы чувствительности, которая в условиях вышеназванных допущений имеет вид
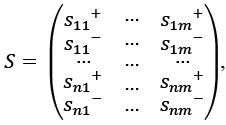
где sij+, sij – - значение чувствительности (2) для j-й альтернативы по i-му критерию.
Если анализировать только чувствительность при выборе j-й альтернативы, то достаточно рассчитать подматрицу:
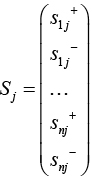 (5)
(5)
и на ее основе принимать решение о принятии или отклонении альтернативы, полученной в результате расчета по алгоритму.
Вычисление sij+ и sij – для каждого i и j проводится при фиксации всех других элементов матрицы (1) на исходных (серединных) значениях. Если в результате вычислений (5) содержит только нули, это говорит о том, что выбор не чувствителен к изменениям значений критериев в заданном диапазоне [х+, х–] и альтернатива «устойчиво» выбирается. В противном случае лицо, принимающее решение, должно взять на себя ответственность в согласии или отклонении альтернативы Vj, учитывая количество единиц N1 в (5). Это количество единиц отражает число ситуаций, когда выбор альтернативы изменялся. Для получения итоговой количественной оценки влияния ![]() на результат вместо N1 также может использоваться норма матрицы:
на результат вместо N1 также может использоваться норма матрицы:
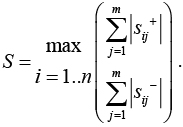
или соответствующее выражение для матрицы (5):
![]() .
.
Очевидно, что значения N1, ||S|| и || Si|| будут зависеть от величины диапазона, характеризуемого величиной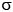 = (х+ – х –)/2, в котором допускается изменение значений функций принадлежности в (1), поэтому параметр
= (х+ – х –)/2, в котором допускается изменение значений функций принадлежности в (1), поэтому параметр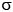 вводится как входной параметр в расчет. Величина
вводится как входной параметр в расчет. Величина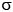 определяет степень требований к обоснованности решения: если при малых значениях
определяет степень требований к обоснованности решения: если при малых значениях 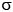 происходит изменение выбора, то, возможно, следует более внимательно и взвешенно подойти к определению значений элементов матрицы (1).
происходит изменение выбора, то, возможно, следует более внимательно и взвешенно подойти к определению значений элементов матрицы (1).
В каком диапазоне![]() допустимо могут изменяться значения функций принадлежности, должно определять лицо, принимающее решение. Здесь нельзя дать однозначные рекомендации, так как все будет зависеть от конкретных условий задачи и предметной области. Возможно, потребуется несколько расчетов с различными значениями
допустимо могут изменяться значения функций принадлежности, должно определять лицо, принимающее решение. Здесь нельзя дать однозначные рекомендации, так как все будет зависеть от конкретных условий задачи и предметной области. Возможно, потребуется несколько расчетов с различными значениями 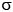 , чтобы оценить границы диапазона, в котором выбор остается неизменным.
, чтобы оценить границы диапазона, в котором выбор остается неизменным.
Предложенный подход к расчету чувствительности метода выбора альтернатив к вариациям значений функций принадлежности в (1) был реализован в системе MatLAB. При разработке программы использовалась среда для созданий графического интерфейса GUI. Общий вид главного окна программы показан на рисунке.
Интерфейс программы интуитивно понятен и позволяет проводить выбор вариантов (альтернатив) по заданным критериям. Количество вариантов и критериев предварительно необходимо задать, после чего сгенерировать таблицу соответствующих размеров для внесения значений функций принадлежности из матрицы (1), указать веса критериев. В поле «диапазон вариаций» указывается значение 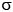 . После ввода исходных данных и нажатия кнопки «провести выбор варианта» программа вычисляет матрицу (3) и номер лучшей альтернативы. Также проводится расчет матрицы (5) при заданном значении
. После ввода исходных данных и нажатия кнопки «провести выбор варианта» программа вычисляет матрицу (3) и номер лучшей альтернативы. Также проводится расчет матрицы (5) при заданном значении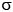 . В дальнейшем предполагается расширение функционала программы с целью построения трехмерных срезов многомерной поверхности функции чувствительности в зависимости от вариаций функций принадлежности различных критериев. Такая визуализация повысит наглядность анализа и дополнительно даст возможность увидеть поведение чувствительности около исходно заданных значений функций принадлежности (1).
. В дальнейшем предполагается расширение функционала программы с целью построения трехмерных срезов многомерной поверхности функции чувствительности в зависимости от вариаций функций принадлежности различных критериев. Такая визуализация повысит наглядность анализа и дополнительно даст возможность увидеть поведение чувствительности около исходно заданных значений функций принадлежности (1).
Подводя итог сказанному, следует отметить, что предложенный подход к анализу чувствительности совершенствует метод выбора альтернатив на основе нечеткого отношения предпочтения за счет дополнительного анализа устойчивости выбора к вариациям значений функций принадлежности в (1). Разработанная в соответствии с предложенной модификацией программа универсальна и может быть применена для обоснованного выбора варианта решения какой-либо проблемы в различных предметных областях.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-07-00491 А.
Литература
1. Бояринов Ю.Г., Стоянова О.В., Дли М.И. Применение нейро-нечеткого метода группового учета аргументов для построения моделей социально-экономических систем // Программные продукты и системы. 2006. № 3. С. 7-11.
2. Бобков В.И., Борисов В.В., Дли М.И., Мешалкин В.П. Моделирование процессов обжига фосфоритовых окатышей в плотном слое // Теоретические основы химической технологии. 2015. Т. 49. № 2.
С. 182-186.
3. Дли М.И., Гимаров В.В., Глушко С.И., Иванова И.В. Интеллектуально-экспертный метод определения оптимального маршрута транспортировки продукции // Программные продукты и системы. 2013. № 4. С. 85-89.
4. Саркисов П.Д., Стоянова О.В., Дли М.И. Принципы управления проектами в сфере наноиндустрии // Теоретические основы химической технологии. 2013. Т. 47. № 1. С. 36-38.
5. Дли М.И., Какатунова Т.В., Скуратова Н.А. Интеллектуальная система управления сложными объектами с использованием нечетких когнитивных карт // Научное обозрение. 2013. № 9. С. 491-495.
6. Андрейченков А.В., Андрейченкова О.Н. Анализ, синтез, планирование решений в экономике.
М.: Финансы и статистика, 2004. 464 с.
7. Кабанихин С.И. Обратные и некорректные задачи. Новосибирск: Сибирское науч. изд-во, 2009.
457 c.
8. Pavlov D.A. The indistinct filter of Kallman in structure of algorithm of the solution of the return tasks for economic objects // Software products and systems, 2013, no. 4, pp. 199-203 (in Russ.).
9. Золин А.Г. Разработка алгоритмов решения обратных задач промышленной диагностики аппроксимационным методом. Автореф. диссер. … к.т.н. Самара, 2010.
10. Дли М.И., Пучков А.Ю., Малевич Е.П. Решение обратных задач на основе нечеткого инверсного калмановского алгоритма // Программные продукты, системы и алгоритмы . 2016. № 2 . С. 5.
11. Кутовой Д.А., Маслова О.И., Перепёлкина С.Ю. и др. Методика оценки характеристик измерителя угловой скорости посредством фильтра Калмана и вариации Аллана // Вестн. Самарского гос. аэрокосмич. ун-та им. С.П. Королёва (НИУ). 2016. Т. 15. № 2. С. 171-182.
12. Вержбицкий В.М. Численные методы (математический анализ и обыкновенные дифференциальные уравнения). М.: Директ-Медиа, 2013. 400 с.
13. Огородников И.Н. Введение в обратные задачи физической диагностики: специальные главы высшей математики для технологов: учебн. пособ. Екатеринбург: Изд-во Урал. ун-та, 2017. 199 с.
14. Дли М.И., Бояринов Ю.Г., Круглов В.В. Оценка диапазона возможных значений вероятности пребывания в заданном состоянии марковской модели производственно-экономической системы // Программные продукты и системы. 2009. № 4. С. 31-35.
15. Абраменкова И.В., Пучков А.Ю., Павлов Д.А. Нейро-нечеткий метод снижения чувствительности решения обратных задач к вариациям данных // Программные продукты и системы. 2011. № 4. С. 72–75.

Comments