В начале 1990-х гг. была разработана область эволюционных вычислений под названием генетическое программирование (ГП) [1, 2]. Его основной идеей было использование эволюционных алгоритмов для создания компьютерных программ. Для представления программ использовался язык программирования Лисп, в котором программы могут легко рассматриваться как структуры дерева. Поэтому вместо обычного использования двоичных последовательностей для отображения решения в ГП в качестве хромосом использовались деревья [2–4].
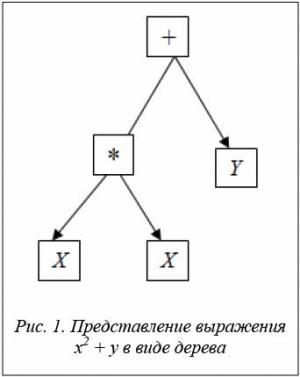
Деревья в ГП составлены из узлов двух типов – узлов функций и узлов терминалов. Узлы функций – внутренние вершины дерева, обычно они соответствуют арифметическим операциям (+, –, *, \, % и т.д.), математическим функциям (синус, косинус, тангенс, логарифм и т.д.), булевским функциям (и, или, не и т.д.), условным операторам (если ... тогда ... иначе), операторам циклов (до тех пор ... пока), любой другой функции из предметной области задачи [2, 5]. Терминалы – листья дерева, соответствующие либо переменной данной области задачи, либо постоянной. Например, выражение x2 + у может быть представлено деревом (рис. 1).
Основу генетического алгоритма составляют принципы кодирования и декодирования хромосом, генетические операторы
и структура генетического поиска [2, 5–7].
Способы представления исходной формулировки задачи в виде трех компонент в очень большой степени определяют усилия, необходимые для ее решения [1, 2].
Гомологичными называют хромосомы, имеющие общее происхождение и поэтому морфологически и генетически сходные, то есть при применении стандартных генетических операторов
не образуются недопустимые хромосомы [8].
В негомологичных хромосомах не может быть двух генов с одинаковым значением. Для негомологичных хромосом применяют различные специальные генетические операторы, которые не создают недопустимых решений. В связи с этим трудоемкость алгоритмов, реализующих генетические операторы для негомологичных хромосом, больше, что увеличивает трудоемкость генетического алгоритма в целом. Это обстоятельство является побудительным мотивом для исследований и разработок гомологичных структур хромосом [9, 10].
Одной из часто используемых моделей при решении многих задач является дерево, в частности бинарное. В работе рассматривается методика представления деревьев с произвольной локальной степенью вершин в виде линейной записи. Предлагаются структура и принципы кодирования гомологичных хромосом, несущих информацию о дереве [10, 11].
Структуры хромосом для деревьев. Рассмотрим структуру выражения для описания бинарного дерева.
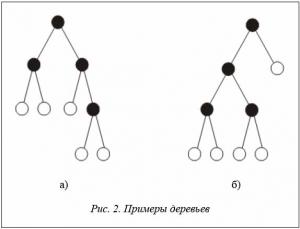
Введем алфавит A = {O, ·}. Структуру бинарного дерева можно задать, используя на базе алфавита A польское выражение, гдеO соответствует листьям дерева, а · – внутренним вершинам дерева. Каждая внутренняя вершина подвергается бинарному ветвлению. Польские выражения для деревьев, представленных на рисунках 2a и 2б, имеют вид O O · O O · O · · иO O · O O · · O ·.
Процесс восстановления дерева по польскому выражению достаточно прост. Слева направо последовательно просматривается польское выражение и отыскиваются буквы типа •, соответствующие внутренним вершинам. Каждая внутренняя вершина объединяет два ближайших подграфа, сформированных на предыдущих шагах и расположенных в польской записи слева от знака •. С помощью скобок покажем подграфы, образованные при просмотре польского выражения слева направо:
{(O O ·) [(O O ·) O ·] ·} и {[(O O ·) (O O ·) ·] O ·}.
Отметим основные свойства польского выражения, выполнение которых необходимо, чтобы ему соответствовало бинарное дерево.
Обозначим через no число элементов польского выражения типа O, а через n· – число элементов типа •. Для дерева всегда выполняется равенство no = n· + 1.
Если в польском выражении провести справа от знака • сечение, то слева от сечения число знаков O больше числа знаков •, по крайней мере, на единицу: no – n· ≥ 1. Первый знак • в польском выражении (при просмотре слева направо) может появиться только после двух знаков O.
Пронумеруем позиции между знаками O:
OO 1 O 2 O 3 O 4 … O no – 1.
Максимальное число знаков ·, которое может появиться в i-й позиции, равно номеру позиции –i. Напомним, что общее число n· = no – 1.
Если польское выражение обладает вышеперечисленными свойствами, то ему соответствует бинарное дерево.
Рассмотрим структуру и принципы кодирования и декодирования хромосомы для представления польского выражения [3].
Хромосома H имеет вид H = {gi | i = 1, 2,…, n·}.
Используем строку с no знаками O в качестве опорного множества для построения польского выражения при декодировании хромосомы.
Число генов в хромосоме равно n·, то есть числу знаков •. Значение Z(gi) гена gi колеблется в пределах от i до n·, то естьi £ Z(gi) £ n·. Значение гена указывает номер позиции между знаками O опорного множества, в которую необходимо поместить знак •. Декодирование хромосом, то есть построение польской записи, осуществляется следующим способом. Формируется базовое множество символов O мощностью no = n· + 1 и определяется n· позиций, расположенных между символами O для помещения в них символов •. Затем последовательно выбираются гены, определяются задаваемые ими номера позиций, в которые и помещаются знаки •.
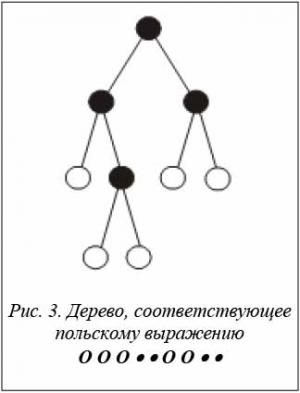
Например, пусть для n· = 4 имеется хромосомаH = <4, 2, 2, 4>. Это значит, что число n o = 5, а число позиций – 4. Два знака • назначаются во вторую позицию, а два знака • – в четвертую. Польское выражение, соответствующее хромосоме, имеет вид
O O O • • O O • •.
Дерево, соответствующее данному польскому выражению, представлено на рисунке 3.
Рассмотрим теперь структуру и принципы формирования линейной записи для иерархического дерева без ограничений на локальную степень внутренних вершин. Запись представляет собой набор элементов A = {ai | i = 1, 2, …, l}, где l – число вершин дерева. Причем n элементов ai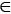 Ao соответствуют листьям дерева, а m элементов ai
Ao соответствуют листьям дерева, а m элементов ai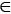 Av соответствуют внутренним вершинам n-арного дерева разрезов:
Av соответствуют внутренним вершинам n-арного дерева разрезов: 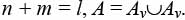
Формирование дерева в соответствии с древовидной записью осуществляется на основе иерархического подхода при просмотре записи слева направо, начиная с первого элемента.
Вершина xi в соответствии с записью расположена слева от xj, если в записи элемент ai расположен левее aj. Древовидная запись организована так, что каждая внутренняя вершина xi, с одной стороны, является корнем некоторого поддерева для вершин, расположенных слева от xi, а с другой – может быть дочерней вершиной для некоторой внутренней вершины, расположенной в соответствии с записью справа от xi. Последнему элементу an списка A соответствует вершина xl, являющаяся корнем всего дерева.
Значением элемента ai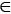 Av, соответствующего внутренней вершине xi, является число поддеревьев, корни которых – дочерние вершины xi. Описания поддеревьев расположены в линейной записи непосредственно слева от ai. Если ai
Av, соответствующего внутренней вершине xi, является число поддеревьев, корни которых – дочерние вершины xi. Описания поддеревьев расположены в линейной записи непосредственно слева от ai. Если ai Ao, то ai = 0, то есть xi является листом дерева.
Ao, то ai = 0, то есть xi является листом дерева.
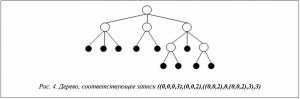
Рассмотрим запись 0,0,0,3,0,0,2,0,0,2,0,0,0,2,3,3. Выделим с помощью скобок иерархически вложенные друг в друга поддеревья, образованные при просмотре записи слева направо: ((0,0,0,3),(0,0,2),((0,0,2),0,(0,0,2),3),3).
Соответствующее дерево представлено на рисунке 4.
Запись дерева обладает следующими свойствами:
- число элементов ai записи с нулевым значением равно числу листьев дерева;
- число элементов ai записи с ненулевым значением колеблется от 1 до n – 1;
- значение любого элемента ai Av, соответствующего внутренней вершине xi, равно или больше
Av, соответствующего внутренней вершине xi, равно или больше
2 (ai ≥ 2), так как при разбиении любая внутренняя вершина связана минимум с двумя дочерними вершинами;
- a1 и a2 всегда равны нулю;
- между номером позиции k и значениями элементов, расположенных в позициях с 1-й по k-ю, существует зависимость
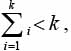
то есть сумма значений элементов, расположенных в позициях с 1-й по k-ю, меньше числа позиций k;
- для записи A = {ai | i = 1, 2, …, l} существует зависимость
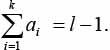
Если запись удовлетворяет перечисленным свойствам, то она является древовидной и ей соответствует некоторое дерево.
Структура и принципы кодирования хромосомы для представления древовидной записи разработаны с учетом вышеперечисленных свойств.
Будем использовать множество элементов ai с нулевым значением в качестве опорного множества
для построения древовидной записи при декодировании хромосомы.
Расположим между этими элементами множество позиций:
0 0 1 0 2 0 3 … n – 2 0 n – 1.
Если число элементов ai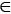 Ao равно n, то число позиций равно n – 1 . В каждую позицию может быть помещено несколько элементов с ненулевыми значениями, но при этом должны быть соблюдены вышеперечисленные свойства.
Ao равно n, то число позиций равно n – 1 . В каждую позицию может быть помещено несколько элементов с ненулевыми значениями, но при этом должны быть соблюдены вышеперечисленные свойства.
Хромосома имеет вид Н = {gi | i =1, 2, …, n – 1}.
Число генов в хромосоме равно n – 1, где n – число листьев дерева. Ген gi может принимать значение в интервале от i до n – 1, кроме того, ген может быть либо помеченным, либо нет. Значение гена указывает номер позиции. Возможны два варианта действий. Если ген не помечен, то в позицию, соответствующую значению гена, к ненулевым элементам последним справа записывается элемент со значением, равным 2. Если же ген помечен, то в соответствующей позиции значение последнего справа ненулевого элемента увеличивается на единицу, а при отсутствии в позиции ненулевых элементов в нее записывается элемент со значением, равным 2. Метки хромосом задаются вектором M = {mi | i = 1, 2, …, n – 1}. mi = 1, если ген gi помечен; mi = 0, если ген gi не помечен. Таким образом, древовидная запись кодируется парой хромосом. Для разметки листьев дерева используется третья хромосома R = {ri | i = 1, 2, …, n}. Пример: пусть задана пара хромосом
Н = {2,2,4,6,9,9,9,9,9};
M = {0,1,0,0,0,0,1,0,1}.
Поскольку число генов в хромосоме Н равно 9, число нулевых элементов в древовидной записи
равно 10. После декодирования пары хромосом H и M полученная древовидная запись имеет вид ((0,0,0,3),(0,0,2),((0,0,2),0,(0,0,2),3),3), а соответствующее ей дерево представлено на рисунке 4.
Предложенные структуры хромосом имеют линейную пространственную сложность.
Разметка множества вершин дерева кодируется двумя хромосомами: H1 содержит информацию
о разметке листьев дерева, H2 – о разметке внутренних вершин дерева.
Если допускается повторение меток, то значением гена в H1 или H2 является метка, которой помечается соответствующая вершина дерева.
Для случая неповторяющихся меток разработаны структура и принципы кодирования хромосом, обладающих свойством гомологичности.
Пусть n – число вершин. Хромосома H1 имеет вид H 1 = <g1, g2 , ..., gn-1 >. В результате декодирования строится вектор R, задающий разметку вершин.
Каждый ген gi может принимать значение в интервале от 1 до (n + 1 – i). Например, для 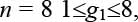
Декодирование хромосомы H1 производится следующим образом. Пусть для n = 8 имеется хромосома H1 = <3,5,3,4,4,2,2> и пусть имеется опорный вектор B1 = <a,b,c,d,e,f,g, h>, число элементов которого равно n. Рассматриваем по порядку гены хромосомы, в соответствии с их значениями выбираем элементы в опорном векторе и записываем их в порядке выборки в вектор R.
Значение g1 = 3. Выбираем в B1 элемент b1j (j = g1 = 3, b1 3 = c) и записываем его на первое место формируемого вектора R, то есть r1 = b13 = с.
Удаляем элемент b13 из B1 и получаем вектор B2 = <a,b,d,e,f,g,h>, содержащий 7 элементов. Следующим выбирается g 2, g2 = 5. Отыскиваем элемент b25 вектора B2:b25 = f. Следовательно, r2 = f. Удаляем
из B2 элемент b25, получаем вектор B3 = <a, b,d,e,g,h>. Далее:
g 3 = 3, b33 = d, r3 = d, B4 = < a,b,e,g,h>; g4 = 4, b44 = g, r4 = g, B5 = < a,b,e,h>;
g 5 = 4, b54 = h, r5 = h, B6 = <a,b,e>; g6 = 2, b62 = b, r6 = b, B7 = <a,e>;
g 7 = 5, b72 = e, r 7 = e, B8 = <a >, r8 = b81 = a.
В итоге получаем вектор <c,f,d,g,h,b ,e,a>, задающий разметку множества вершин.
Генетические операторы. Основными генетическими операторами являются кроссинговер и мутация [1, 2, 8].
У описанной выше структуры хромосом гены, расположенные в одних и тех же локусах, являются гомологичными. Реализация кроссинговера осуществляется следующим образом [4–6].
У предварительно выбранной родительской пары хромосом (на основе использования принципа рулетки) последовательно просматриваются гомологичные пары генов, и с вероятностью Pk осуществляется обмен генами. При таком подходе степень модификации родительских хромосом определяется значением параметра РК.
Суть оператора мутации в произвольном изменении значений генов. Реализация оператора мутации осуществляется следующим образом. Последовательно просматриваются хромосомы, и с вероятностью РМ 1 они подвергаются мутации. Если хромосома мутирует, то последовательно просматриваются локусы хромосомы и с вероятностью РМ2 осуществляется мутация гена в рассматриваемом локусе. Мутация заключается в принятии геном случайного значения из заданного диапазона значений для гена в данном локусе [4–6].
Представление решения в виде набора хромосом дает возможность использовать оператор комбинирования набором хромосом в одном решении, что является приближением к естественной эволюции.
С другой стороны, представление решения набором из n хромосом дает возможность организации поиска решений в различных постановках, оставляя отдельные виды хромосом неизменными в процессе генетического поиска [11].
Очевидно, что фиксация отдельных хромосом в некоторой постановке приводит к сужению пространства поиска, и при этом возможна потеря оптимальных решений. В этой связи представляется целесообразным комбинирование отдельными постановками при поиске оптимального решения [10, 11].
В общем случае возможны три подхода к комбинированию постановок: последовательный, параллельный и параллельно-последовательный.
При последовательном подходе на каждом i-м этапе осуществляется генетический поиск путем модификации хромосом, входящих в заданный для этого этапа набор NHi модифицируемых типов хромосом. Это означает, что в полном объеме используется кроссинговер К1, заключающийся в комбинировании наборов хромосом, входящих в решение, а кроссинговер К2 и мутация применяются только к тем хромосомам, которые входят в набор типов модифицируемых хромосом.
Приведем комбинацию, при которой в наборы входят по одному типу хромосом:NH1 = {H1}, NH2 =
= {H2}, NH3 = { H3}. В набор могут входить от одного до четырех типов хромосом. На первом этапе в качестве исходной служит популяция Пи. На втором – популяция П1, сформированная после отработки первого этапа, и т.д. Отметим возможность циклического повторения этапов.
При параллельном поиске производится распараллеливание процесса генетического поиска.
Вначале формируется исходная популяция. Для каждой параллельной ветви задается набор NHi типов хромосом, подвергающихся модификации. Затем на первом шаге на базе этой исходной популяции
на каждой параллельной ветви осуществляется генетический поиск путем модификации хромосом, входящих в соответствующий набор типов модификаций хромосом.
После некоторого числа генераций (поколений) осуществляется случайное или направленное перемещение хромосом между любыми популяциями П 1–П3, сформированными на данный момент на параллельных ветвях. После этого на втором шаге модифицированные популяции П10–П30 вновь подвергаются обработке генетическими процедурами на параллельных ветвях. Число шагов является управляющим параметром [8, 10, 11].
При параллельно-последовательном подходе на каждой параллельной ветви реализуется последовательная комбинация постановок.
Как видно из алгоритмов, реализующих операторы кроссинговера и мутации, оценка их временной сложности на итерации имеет вид O(n).
Заключение . Рассмотренные в работе новые принципы и способы кодирования и декодирования хромосом для представления деревьев исключают некорректные решения, отличаются простотой и линейными оценками временной и пространственной сложности, что упрощает использование генетических операторов и позволяет использовать модификации генетических операторов, близких к естественным.
Многохромосомные представления решений позволили создать иерархические структуры генетических операторов, что дает возможность организовать целенаправленный поиск.
Предложенные процедуры кодирования и декодирования повышают целенаправленность поиска, включают процедуры улучшения решения и обеспечивают более высокую вероятность локализации глобального экстремума задачи. В среднем это позволяет повысить на 2–4 % качество решения.
Работа выполнена при финансовой поддержке гранта РФФИ № 17-07-00997.
Литература
1. Quagliarella D. [et all], eds. Genetic algorithms and evolution strategy in engineering and computer science. John Wiley & Song, 1998.
2. Davis L., Ed. Handbook of Genetic Algorithms. NY, van Nostrand Reinhold, 1991, 385 p.
3. Гладков Л.А., Зинченко Л.А., Курейчик В.В. Методы генетического поиска. Таганрог: Изд-во ТРТУ, 2002. 145 с.
4. Лебедев Б.К. Интеллектуальные процедуры синтеза топологии СБИС. Таганрог: Изд-во ТРТУ, 2003. 108 с.
5. Курейчик В.В. Эволюционные, синергетические и гомеостатические методы принятия решений. Таганрог: Изд-во ТРТУ, 2001. 221 с.
6. Курейчик В.В., Родзин С.И. Концепция эволюционных вычислений, инспирированных природными системами // Изв. ТРТУ. Тематич. вып.: Интеллектуальные САПР. 2009. № 4. С. 16–25.
7. Тарасов В.Б., Голубин А.В. Эволюционное проектирование: на границе между проектированием и самоорганизацией // Изв. ТРТУ. Тематич. вып.: Интеллектуальные САПР. 2006. № 8. С. 77–82.
8. Гладков Л.А., Курейчик В.В., Курейчик В.М., Сороколетов П.В. Биоинспирированные методы в оптимизации. М.: Физматлит, 2009. 384 с.
9. Норенков И.П. Основы автоматизированного проектирования. М.: Изд-во МГТУ им. Баумана, 2006. 348 с.
10. Лебедев О.Б. Синтез дерева разрезов при планировании на основе метода муравьиной колонии // Интегрированные модели и мягкие вычисления в искусственном интеллекте: матер. VI Междунар. науч.-практич. конф. М.: Физматлит, 2011. № 1. С. 521–529.
11. Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой. М.: Изд-во МГТУ им. Н.Э. Баумана, 2014. 448 с.
Comments